基于三因子模型的非市场风险溢价改进

■王一 叶方 施继荣

我国证券业发展时间较短，通过历史收益预测未来的收益率中，可能没法准确判断长期趋势。评估师们在选择参数时不太会考虑到由过去推测未来应做的调整。特别是非市场溢价部分，当前的计算标准缺乏，估算方法不一，并没有一个统一标准或者准确的模型可供使用，评估师往往依靠经验和主观判断得出的非市场风险溢价。

三因子模型是价值评估中计算折现率非常前沿的一种方法，是资本资产定价模型的进一步发展，三因子模型将市场股票组合、公司规模和公司普通股的账面价值市值比和变动敏感因子加入到资本资产定价模型中。三因子模型是资本资产定价模型的扩展也是近些年比较流行的发展趋势。

本文在已有的三因子模型基础上进行改进，把普通股的账面价值市值比引入新的模型中，采用科学的模型和计量方法衡量非市场风险溢价水平，使结果更加科学可靠。

一、关于三因子模型

三因子模型是指Fama-French三因子模型，是一种改进的资本资产定价模型理论。该模型基于美国股市过去回报率的实证研究结果，目的在于诠释股票市场的均匀回报率遭到哪些风险溢价成分的偏差。

Fama和French（1993）在美国股票市场上利用资本资产定价模型挖掘，资本资产定价模型在股票的β值与截面数据的平均股票回报的相关性弱，股票平均收益数据的解释能力率低。因而，他们建立了三个市场组合，公司规模，ME（普通股本账户的企业价值和股票市场价值），这两个因素相关的风险因素加入资本资产定价模型，由此树立起新的三因子资本资产定价模型。此模式很好地诠释了1963年到1990的NYSE、AMEX、NASDAQ等股票市场的截面数据的均匀收益率。三因子模型是资本资产定价模型的有效拓展，同时也是资本资产定价范畴的里程碑式的模型。

在资本资产定价模型等传统理论下，投资组合的全部风险溢价由Beta系数表示。但是这个模型在现实中解释股票市场的回报，遇到了许多挑战。Fama和French（1993）通过模拟市场风险、市值风险和账面市值比风险构造了三因子，用来解释股票收益的变化。模型认为，一个投资组合（包括单个股票）的超额回报率可由它对三个因子的暴露来解释，这三个因子是：市场资产组合（Km－Rf）、市值因子（SMB）、账面市值比因子(HML)。这个多因子均衡定价模型可以表示为：

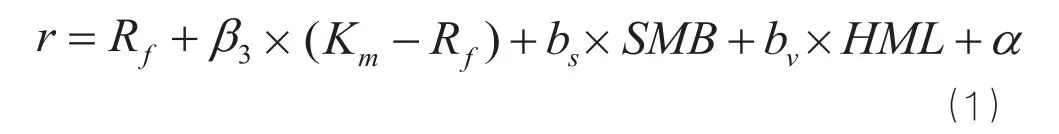
其中：r是投资组合的期望回报率；Rf是市场无风险回报率；Km是市场组合的回报率。

三个变量的估计系数β是一个混合的市场风险溢价，溢价率的变化，三个因素对预期收益率的净影响；股市搭配风险溢价的系数beta观念近似于资本资产定价模型模式中的beta系数，公司规模可变的SMB是一个小企业的投资组合回报的市场价值和组成的投资组合收益差异的大型公司的市场价值；市净率溢价HML是账面价格相对高的公司组成的投资组合回报与比值较低的公司投资组合回报之差；是逾额收益率，在完美的情况下，投资搭配的超额回报将统统被三种成分诠释，从而应在统计学意义上即是0。

资本资产定价模型把资产组合与整个股票市场结合到了一起，它的媒介是市场的Beta系数这一单一因子。但是经过Fama和French的探索发现，股票市场上，同一时刻不同股之间的差异无法用资本资产定价模型来解释，因此Fama和French认为将市场风险因子Beta作为单一的影响因素是错误的，由此加入了公司规模和市净率溢价这两个变量，并且仍然把市场风险放在重要的位置，得出一个新的模型，三因子模型。Small Minus Big 简称SMB，是为了衡量公司规模产生的溢价。市值相对小的公司股票会给投资者带来超过大盘平均表现的历史收益。像SMB这样通过公司市值大小引起的溢价叫做规模溢价。因此在同一时间段内，市值小的公司股票表现会优于市值大的公司股票或者投资组合。High Minus Low简称HML，用来表示账面价值溢价。账面价值比高的股票会给投资者带来溢价，也就是说在一定的一段时间内，价值股的表现要超过成长个的表现。

基于Fama-French的三因子模型，Carhart（1997）发表了四因子模型。Carhart四因子模型对股票的系统风险控制，调整原有的回报，然后获得超额收益的风险因素控制。Carhart四因子模型是对Fama-French三因子的模型的改良，包括了股市因子（Market Factor），大小因子（Size Factor），价值因素（价值系数）和动量因子。

二、基于三因子模型的非市场风险溢价计算

因为自由现金流是以年计算的，所以本研究所用的数据均调整为以年为单位。如果数据库里只能采集到日回报率的样本，一般是采用日回报率的算数平均数或者几何平均数来转化为年回报率。

（一）无风险报酬率的计算

无风险报酬率又称单纯利率，是指在无风险和没有通货膨胀情况下的平衡利率，就是在本金没有失信风险、预期收入获得保障时的本钱价格。无风险报酬率并非一成不变，它跟随相关成分的转变而不断变化。无风险利率，由平均利润率决定，主要影响供应和资金需求与政府规制。一般情况下，无风险报酬率能够参考中长期国债的利率或同期银行的存款利率来确定。外国有关咨询机构大多把持久国债利率变为无风险报酬率，而中国许多评估机构与证券公司以较长期限银行存款利率作为无风险报酬率。无论以哪种利率作为无风险报酬率，均应从利率的安全性和风险性两个方面动手，剖析国债的根本特征和我国国债发行与利率变更，分析长期银行存款利率和利率变化的基本特征。

1.计算方法

国债和其他证券的安全，即相比之下，发行人是中央政府，国家主权和资源是国家的偿债责任的基础，有最高的信誉，是最安全的。同时，政府债券的安全性是基于金融机构、企业和个人都愿意持有国债，很容易被当前的市场价格出售债券，是最具流动性的政府债券。此外，美国国债收益率是相对稳定的，预期收益的风险最小，因为易于偿还。可以说，国债是危险最小，收益最巩固，最平安的有价证券。在国际上，国债利率不足同期银行存款利率，是当之无愧的基准利率，因此，把国债利率当做无风险报酬率是科学、公道的。

上世纪80年代，我国国债发行基本上采纳行政体系分派的办法，1994年全部开始借鉴西方流行的承销方法发行。国债发行的基本目的在于筹集建设本金，于是，经过行政方法确定国债发行利率高于储蓄存款利率，以加强国债的吸引力，一般比银行存款利率1-2个百分点，到1999年9月国债在银行间债券市场利率招标发行。每一个区间都是一定的利差招标投标的时间间隔（如0.25%-0.65%）、利差变动范围（如0.01%）。但5年期国债利率仍高于同期银行存款利率0.43%（3.31%-2.88%）。

因为国债利率是用单利表现的，而企业估值中利用的折现率是复利方式，所以，不可以直接把国债利率作为无风险报酬率，而要对国债利率进行修改，修改后的利率作为无风险利率的回报。其计算公式为：

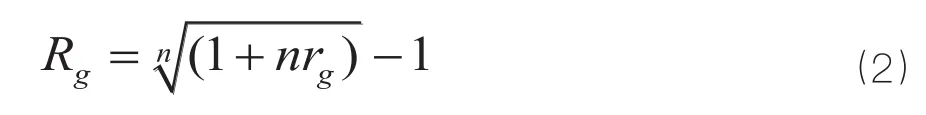
式中，Rg为在国家债务利息的复合形式；rg为单利形式的国债利率。

2.期限选择

要估计无风险报酬率，不妨参考不存在违约风险的国债。国债有很多种期限。中国财政部发布的国债，期限从短期到中期到长期国债。不同的国债有不同的到期日。

按照理想情况来说，应该每一个预期未来现金流要对应一个到期日和它接近的国债来折现。例如，一个5年后产生的折现现金流应该根据5年期国债的利率来折现。

但是在评估实务中，很少有人把每一个预期现金流都匹配一个到期收益率的。为了方便起见，所有评估师都会选择与整个未来预期现金流最为匹配的一种国债到期收益率。对于中国企业而言，企业估值最常用的是5年期国债，更长期的国债，比如20年期国债，可能更贴近于现金流的时间，但是20年期国债缺乏流动性，如果要在二手市场上购买这样的一个20年期国债，就要付出更多的交易费，得到更少的利息，显然会错误估计最终的无风险收益率。

在为公司作长期项目评估时，不能使用短期国债收益率作为无风险收益率。否则会错误估计长期项目的资本成本。但是美国采用10年期政府债券收益率。因为美国评估界折现现金流的预测期为10年，为了和现金流的预测期一致，所以采用10年政府债券收益率作为无风险报酬率。

我国的评估师对未来现金流的预测一般都是5年期，对应的无风险报酬率应该采用5年期的国债利率。

评估实务界一般采用从评估基准日到国债到期日剩余期限5年以上国债的平均到期收益率。但是不同评估师算出来的5年期国债平均到期收益率也不同。

选择5年以上国债的平均到期收益率还是银行5年期存款利率也是一个争论点。

近24年5年期存款利率发生了很大的变化。近10年一直处于波动中。从2004年的3.6%升到最高峰2007年的5.85%再降到2008年的3.6%。最近一次调整是2012年的4.75%。

五年以上到期的国债票面利率没有什么趋势性的变化，说明以后五年的无风险利率还是保持了这个水平。

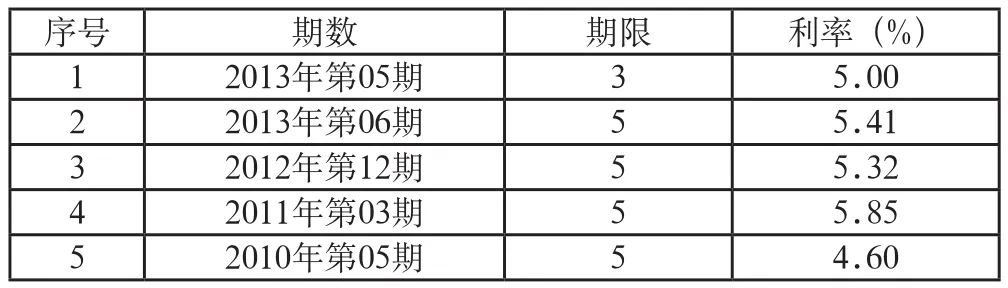
表1 国债利率表

到2013年12月31日为止，五年以上到期的国债的平均票面收益率为3.8524%。由于银行五年定期存款的收益率一直处于波动之中，而5年以上的国债票面利率一直保持稳定的趋势，不增也不减，无风险报酬率的平均数是用超过五年到期的债务利息率。这样较好的衡量以后5年的无风险报酬率。

（二）系统风险报酬率

跟股票的未来收益不可预测一样，市场的未来收益也是没有办法观测的。通常情况下评估师有三种方法来估测市场的风险溢价。

一是通过计算过去的超额回报率来估算未来的风险溢价。

二是运用当前的市场变量，比如股息总额和股价之比来进行回归分析，估测市场风险溢价。

三是折现现金流估值法，再加上对投资回报率ROIC和增长率G的估测，来得出市场风险溢价。

1.综合市场报酬率

国内的评估界通常使用历史的市场风险溢价来估算未来的市场风险溢价，如果投资者是风险厌恶型的，那么他就对股票高于债权的风险需要一定的风险补偿。在过去的投资者和未来的投资者的风险厌恶程度不变的话，市场风险补偿就不变。

在计算时要注意采用长期国债的利率，市场收益率也要采用尽可能长的时间。对于较长的时间间隔可以使用算术平均值；最后是调整好偏差。

就算是十年的回报率也会有很大的不同。美国在20世纪50年代的股票回报率超过了债券回报率18%，然而到了20世纪70年代两者回报率就差不多了。由于没有明确的线性趋势可以预测，短期内发生巨变的可能性也很大，因此应该采用长期回报率。

（1）算术平均与几何平均的比较

在计算市场风险溢价时，我们要的是年度收益率，然而怎么把几十年的长期数据转化成为年度数据是一个问题。

每年的回报率可以由算术平均法计算。算术平均法是所有的年收入加起来，除以年数。

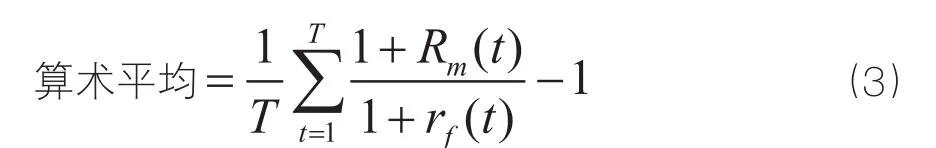
其中：T为年数；

Rm为市场收益率；

rf为无风险收益率。

几何平均法就是把每年的超额收益率相乘再取T次方根，再减去1。

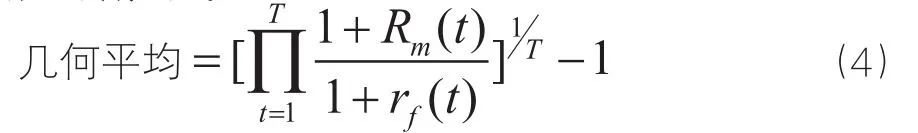
算术平均和几何平均的结果可能相差很大。1903-2002年这100年间，美国的每年股票收益率超过10年以上政府债券的6.2%，这是用算数平均数的结果。然而用几何平均数时，这个数字缩小到4.4%。这不是偶然结果，因为当回报率的方差很大时，几何平均数总是小于算数平均数。

对于历史数据估计未来预期，使用哪种平均方法是一个首要解决的问题。要估算股票收益率的期望值或者平均值，最佳使用方法是算术平均值，也是最好的无偏估计值。所以，要是求得一只股票在一段时间内的预期收益率，最好的无偏估计办法就是对几个不同时间段的同一股票的收益率进行计算，求出平均值。但是，仅仅凭一段时间的股票风险溢价是无法估测现金流预测期有很长几年时的企业价值。几年以后的现金流必须使用长期观察的回报率来折现。不过，经过加权平均以后，算术平均值会比几何平均值高。

这个误差主要来自于估算中的误差和回报率的自相关。

当出现回报率负的自相关时，也就是高的回报率后面紧接着低的回报率，低回报率后面又紧接着高的回报率。这时候算术平均值就会偏高。

根据国泰安数据服务中心，CSMAR数据库，股票市场系列，中国证券市场指数研究数据库，交易数据查得沪深300指数的数据从2005年4月11日开始的，从2005年4月11日到2013年12月31日期间的交易日日回报率的算术平均数为0.06%，并且2013年的交易日数为238天，上海和深圳300指数的年回报率为13.50%。

（2）通货膨胀对沪深300指数的影响

以上推出的沪深300指数的回报率没有扣除通货膨胀率的影响。根据过去20年的通胀形势，1994年至2012年期间官方公布的居民消费价格指数的算术平均值为4.21%，2005年至2012年期间官方公布的居民消费价格指数的算术平均值为3.07%。差距原因是1994-1996年这三年的居民消费价格指数非常高。以后居民消费价格指数的趋势如果稳定在3.07%左右，那么沪深300指数的平均收益率没必要做什么调整。

（3）综合市场的报酬率

综合市场的报酬率不需要做太大的调整。市场风险溢价为13.50%-3.85%=9.65%。我不认为这个数值偏高。美国的市场风险溢价在3.5%-4.5%之间。中国的股市本来就波动剧烈，受其他因素干扰比较大，风险性更大，所以市场风险溢价更高。

但是我并不同意科勒在价值评估一书中指出的，发展中国家采用的综合市场报酬率应该采用标准普尔500指数或者是欧洲市场的综合指数。科勒指出，发展中国家的综合指数只会涵盖某几个行业，所以求出的beta系数就是被评估公司的收益率和某几个行业的变化敏感因子。但是我个人对这个观点有所疑惑，如果在我国根本不存在美国或者欧洲或者综合指数里面的某些冷门行业，那么也没有必要求出被评估公司的股票收益率与美国或者欧洲综合市场指数的变动敏感因子beta。毕竟中国的股市受宏观政策的影响还是很大的，在一个政策与市场共同干预的情况下，沪深300指数更能反映标准普尔500指数所不能解释的影响因子。在CRSP网站上可以查到，这是一个Fama-French自创的网站，里面有1926年以来美国综合市场NYSE、AMEX和NASDAQ的收益率，近八年的几何平均值为6.37%，比使用沪深300指数低了近一半，扣除无风险收益率，就只剩下0.96%，市场风险溢价低到这个程度显然大家都无法接受，也就是说在中国买股票的收益率也就比存五年期的定期存款利率高出一点点。

数据来源于CRSP网站，是由Fama-French自己成立的一个网站，公布每一期SMB和HML的溢价。它的市场风险溢价中的综合市场收益来自于NYSE、AMEX和NASDAQ，数据从1926年7月份开始。但是最近十年受金融危机影响，市场风险溢价波动剧烈。2006年的市场风险溢价为10.59%，2007年的市场风险溢价为1.05%，2008年的市场风险溢价为-38.35%，2009年的市场风险溢价为28.27%，2010年的市场风险溢价为17.39%，2011年的市场风险溢价为0.47%，2012年的市场风险溢价为16.29%，2013年的市场风险溢价为35.21%。八年的风险溢价算数平均值是8.86%，几何平均数是6.37%。如果要计算中国股票和美国综合市场变化的敏感系数，应该对应美国前一天的股市，因为纽约比中国晚了13个小时，只有前一天的美国股市会给中国股市带来影响，而非13个小时以后的美国股市给中国股市带来影响。要选取60个交易日的情况，而美国股市在感恩节和圣诞节的时候停市一天，所以要把中国股市这两天以后的反映去掉，做出来的回归才不会交错。

在对所选股票的美国市场风险溢价做回归时，得出的相关系数只有0.21，显然两者回归关系不显著，相关系数如下：

但是所选股票和沪深300指数做出来的回归就比较好，见表3所示。

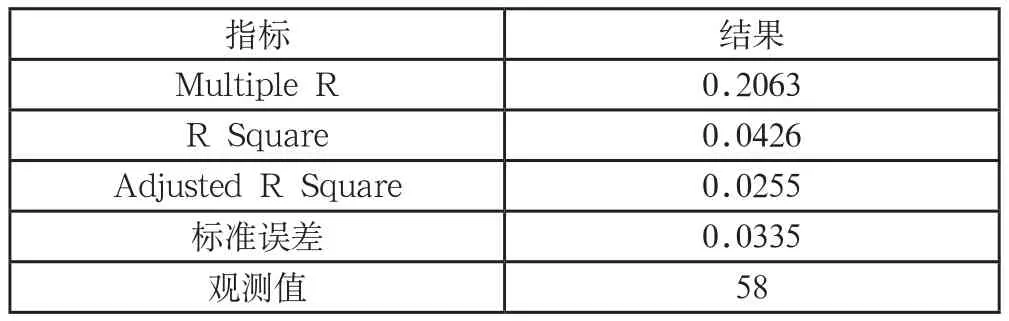
表2 所选股收益率和美国综合市场风险溢价的回归结果

表3 所选股收益率和中国综合市场风险溢价的回归结果

2.估算beta值

在资本资产定价模型中，股票的未来期望收益率受β影响很大。β又称为风险敏感因子。它反映了股票和市场受风险影响变动的幅度。由于我们的单个股票β值不能直接从公司年报上读到。必须通过一系列计算得出结论。在市场中，把市场收益率对股票收益率做回归。通过回归的方法求出原始的β值。

有几点要注意的是：

首先，β系数的原始回归数字要大于等于60个数据点，如果是月回报率的话，就要取5年的值。β值的变化轨迹能够用图形表示出来。这样一眼就能看出股票的系统性风险变化。

其次，β值的原始回归方程应该基于月收益率数据。若是使用日收益率或者周收益率等等更短的期间，会导致回归出现系统性偏差。

最后，企业的股票收益率应该对应的是经过加权平均的价值和充分分散化的组合，比如沪深300指数或者标准普尔500进行回归。到底使用中国的沪深300指数还是标准普尔500指数，在下文计算市场风险溢价的时候还是要展开说明的。

（1）该企业的beta值

利用国泰安数据服务中心的中国股票市场风险评估系数β数据库。2013年12月25日该公司综合市场年beta值为1.1234。

原始beta值是公司有杠杆的beta值。无杠杆的beta值和有杠杆的beta值的关系是：

其中，βe是有杠杆的beta值；

βu是无杠杆的beta值；

D是公司的负债；

E是公司的所有者权益。

2012年第二季度的资产负债比为18.7%，2012年第三季度的资产负债比为29.84%，2012年第四季度的资产负债比为31.83%，2013年第一季度的资产负债比为32.61%，2013年第二季度的资产负债比为30.95%，2013年第三季度的资产负债比为36.05%。

把2013年的资产负债比算术平均一下，得到的结果是33.2%。

所以无杠杆的beta值是1.1234×（1-33.2%）=0.75

（2）同业竞争者的beta值

接着要计算竞争对手的beta值，此公司在行业里的竞争对手有很多家，这里选择和它实力差不多的另外三家的beta值。

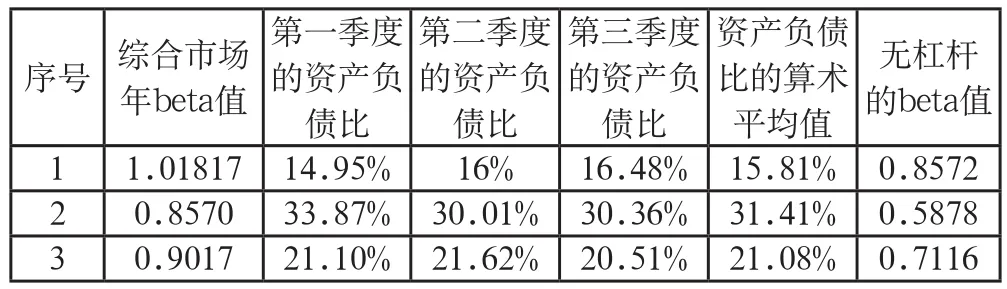
表4 行业内竞争对手2013年beta值

这四家公司无杠杆beta的中位数是0.7308，算数平均数是0.7267，所以行业的平均beta是0.7267，再根据目标公司的资产负债比得出有杠杆的beta是0.7267/（1-33.2%）=1.0878

所以公司的无风险报酬加市场风险溢价为3.85%+1.0878×（9.65%）=14.35%

（三）非系统性风险报酬率

下面计算公司的非系统性风险溢价，通常是公司规模溢价和市净率溢价。

国内对这方面的研究很不成熟，基本上是靠评估师的主观判断和从业经验决定的。数据缺失和我国企业价值市场不完善也是一个重要的原因。

1.规模报酬溢价

照理说求出股票收益率相对SMB和HML变动的beta系数应该采用月度数据，因为当这只股票交易很少时，采用日回报率或者是周回报率就会出现很大的问题。股票要是缺乏流动性就会出现零回报率的报告，本次研究的股票在取的60个交易日数据里面就会出现这样零回报率的情况，并不是因为股票在这一交易日的价值不变而是因为这一天的股票没有交易。采用比较长期的股票回报率，比如说是月回报率，就不会出现这样的情况。

采用非常短期的数据的另一个问题是买卖价差，某一瞬间的股票价格取决于交易双方的竞价，股票价格就会从上一个卖家的价格直接跳到下一个卖家价格，在两者之间不断跳跃，从而会扭曲了beta系数的估值。对所研究的股票收益率和SMB和HML做回归时，发现选定股票的收益率与SMB的关系如下

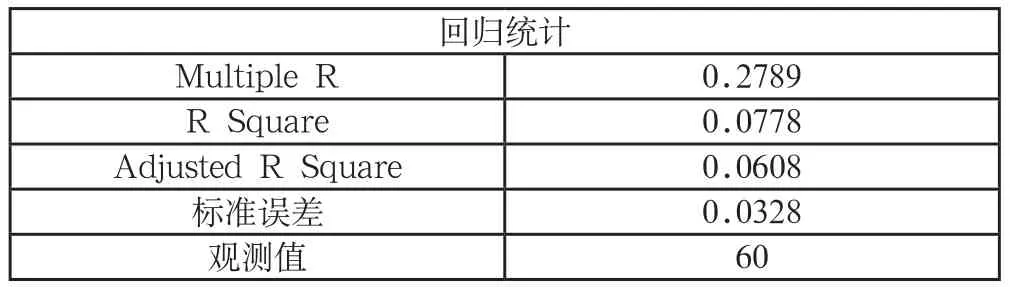
表5 所选股收益率与规模风险溢价的回归分析结果

本文采用的S M B数值来源于国泰安数据库的CSMAR数据库，股票市场系列，中国证券市场指数研究数据库，交易数据，SMB的计算方法是找出上证超级大盘2013年10-12月的日收益率，减去上证中小盘2013年10-12月的日收益率，得到SMB的收益率。一般性指流通股本超过一个亿的股为大盘股，流通股本超过10个亿的是超级大盘股，流通市值低于一个亿但是高于5千万的是中盘股，流通市值低于5千万的是小盘股。

2.普通股账面价值-市值比溢价

发现选定股票的收益率与HML的关系如下

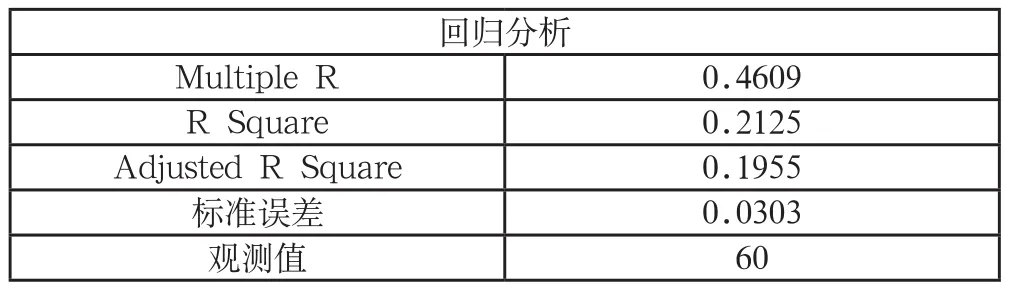
表6 所选股收益率与普通股账面价值-市值比溢价的回归分析结果

本文采用的HML数值来源于国泰安CSMAR数据库的股票市场系列，中国证券市场指数研究数据库的交易数据，HML的计算方法是找出上证全指成长股2013年10-12月的日收益率，减去上证全指价值股2013年10-12月的日收益率，得到HML的收益率。成长股指的是市价比上账面价值高的股，价值股是市价比上账面价值低的股。

但是如上图所示，做出的回归告诉我，自选股的收益率与公司规模溢价的关系不大，公司越小，规模溢价越大。

不过，自选股的收益率与市价与账面价值之比关系很大，市价与账面价值高的公司风险溢价大。

本文把HML这个变量加入到计算自选股收益率的模型当中。把自选股的收益率和市价账面价值溢价进行拟合。使用excel中的拟合公式。

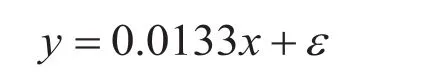
其中，y为自选股收益率；

X为市价账面值溢价；

为残差项；

拟合的R2等于0.93，通过检验；

0.0133 为求得的beta系数。

2013年最后三个月的HML算数平均值为-2.08375%，所以HML的风险溢价为-2.0838%×0.0133=-0.0277%。综上所述自选股的回报率为14.3468%-0.028%=14.3191%

三、结论

本文把自选股的收益率分为三部分，即无风险报酬率、市场风险溢价和非市场风险溢价，计算这三部分收益率的时候都采用通过历史数据调整的方法来预测未来的收益。

（一）无风险溢价采用五年以上到期的国债票面利率

在计算无风险收益率时发现采用五年以上到期的国债票面利率会比使用银行五年期定期存款利率更为稳定，能够真正代表未来的水平。如果仅仅采用五年期整到期的国债票面利率，会使得无风险回报率大大降低，因为债券的期限越长，回报率越高。

（二）市场风险溢价采用名义综合市场收益率

在计算市场风险溢价的时候，没有采用美国综合市场的指数，尽管美国综合市场的指数，例如标准普尔500和纳斯达克指数涵盖的行业更加全面，能够代表整个市场的状况，而不会像沪深300指数，比较侧重于重工业等行业，会导致做来的效果是自选股和某些重工业之间的变化关系。但是经过回归分析发现，所研究的股票收益率和美国综合市场指数的相关系数绝对值太小，无法证明二者存在怎样的变化关系。所以还是选用了沪深300指数作为综合市场指数。

另外，再算出综合市场风险溢价之后还必须考虑未来的通货膨胀率变化会对市场风险溢价带来的影响。如果未来的通货膨胀率预期升高1%，那么市场风险溢价要降低1%；反之，未来通货膨胀率会减低1%，那么市场风险溢价要升高1%。毕竟综合市场收益率没有扣除通货膨胀的影响，因此，本文采用的是名义综合市场收益率，而非实际的综合市场收益率。

（三）非市场风险溢价引入SMB和HML

在计算非市场风险溢价的时候引入了两个变量，被证明在美国的股票市场对解释股票收益率非常有用。一个是公司规模报酬溢价，又称SMB（Small Minus Big）公司越小，风险溢价越高。另一个是市值账面价值比溢价，HML（High Minus Low）市值账面价值比越高，俗称成长股，风险溢价越高。但是经过回归分析，发现SMB在解释所选股收益率时的相关度不大，也就是说所选股的规模风险溢价不明显，但是所选股与市值账面价值比溢价关系比较大，后者能够给股价带来一定的影响。

计算折现率时考虑到非市场风险溢价是一种评估界的流行趋势，评估师争相使用这种方法，也诞生了无数种奇思妙想的变量，有的评估师把公司的资本结构考虑进去，认为过高的负债比会影响被评估公司的非市场风险溢价，但是这种判断多半基于经验极其丰富、职业道德极其崇高、肩负委托方神圣使命的资深评估师身上。毕竟没有简单可靠的模型，或者指数，可供我们评估人员来使用。

四、讨论

（一）非市场风险溢价测算时考虑更多的因素

影响非市场风险溢价的因素很多，包括账面市值比、规模因素、市盈率、市净率。可以把所有影响折现率的因素都拿来拟合，前提条件是这些因素所对应的数据能够从国内数据库上找到。这次的非市场风险溢价只加入了一个变量，就是普通股账面价值-市值比溢价，其实通过更长时间的研究应该可以找到更多的变量，能够对最终的折现率产生影响。并且普通股账面价值-市值比溢价这个变量对最终的折现率影响也不是很大。

（二）引入特尔菲法评估非市场风险溢价

很多评估人员已经开始使用评分法评估非市场风险溢价，首先要收集信息，选择影响因素作为指标，并且确定各项指标的权重。其次是确定打分标准。评估模型只是一个框架，需要有数理统计方法对数据进行测算。而采取不同的算法，即使是对同一对象，所得到的测评结果也可能是不同的，甚至有较大的差别。

因此在开展研究中，要根据评估对象的实际情况，根据指标体系的特点采取合适的算法。在统计软件例如SPSS和AMOS等得以普遍应用的前提下，借用统计软件来开展数据分析大大提高了分析的效率，也在一定程度上保障了数据分析的精确性。这不失为另一种很好的评估非市场风险溢价的方法。

[1]Fama E F,French K R.Common risk factors in the returns on stocks and bonds[J]. Journal of Financial Economics,1993,33(93):3-56.

[2]Belo Frederico. Brand capital and firm value[J].Review of Economic Dynamics. 2014, 17(1): 150-169.

[3]Blake David. Age-dependent investing: Optimal funding and investment strategies in defined contribution pension plans when members are rational life cycle financial planners[J].Journal of Economic Dynamics and Control. 2014, 38(1): 105–124.

[4]胡晓明,冯军.企业估值折现率确定基于资本资产定价模型[J].会计之友,2014(2):18-23.

[5]兰春华.净现值法中基准折现率的影响因素分析[J].中国证券期货, 2013(5): 331-333.

[6]李延喜.基于动态现金流量的企业价值评估模型研究[D].大连:大连理工大学,2002.

[7]刘维奇,牛晋霞,张信东.股权分置改革与资本市场效率[J].会计研究,2010(3):65-72.

[8]屠新曙,韦宏.资本资产定价模型的使用条件分析[J].华南师范大学学报,2013(5):36-39.

[9]杨晶.折现率与价值评估问题探析[J].中国管理信息化,2013(1):8-9.

[10]杨景芝,吴聪.企业价值评估中折现率确定方法理论探讨[J].商业会计,2013(2)::68-69.

[11]赵邦宏,王哲,宗义湘.资本资产定价模型企在业价值评估中的应用[J].河北农业大学学报,2005(5):98-103.

[12]赵强,苏一纯.企业价值评估中折现率的估算方法[J].中国资产评估,2001(6):17-19.

[13]赵强.折现率估算的误区解析[J].中国资产评估,2002(3):11-13.

[14]赵强.折现率估算中的物价指数[J].中国资产评估,2013(6):14-16.