基于市场波动经济预测的公允价值计量方法研究

李　悦



基于市场波动经济预测的公允价值计量方法研究

李悦

摘要：市场波动经济指数的非线性变化对公允价值的计量带来不确定输入值，为了提高对市场计量的公允价值的估价准确性，提出一种基于非线性经济指数序列分析和市场波动经济预测的公允价值计量方法。构建了市场波动经济指数的非线性序列分析模型，采用最大Lyapunov指数特征提取方法得到公允价值计量的输入参量特征，结合平均互信息方法构建一个状态预估计器，实现市场波动的经济预测，以此实现公允价值计量方法的改进。数据仿真测试结果表明，采用该计算方法进行市场波动经济条件下的公允价值计量和经济指数预测，具有较高的准确性，算法的收敛性和稳定性较好，精度高于传统计量方法，对金融利率、价格波动性、信用风险等参数的评估性能较高。

关键词：市场波动；经济预测；公允价值；计量方法

一、引言

公允价值的计量是衡量金融经济和货币流通性能的通用标准之一，公允价值的定义为市场参与者在计量日发生的有序交易中，出售一项资产所能收到或者转移一项负债所需支付的价格。通过公允价值计量方法的优化，对公允准则的初始计量、估值技术得到有效提高，使得交易双方在熟悉市场情况下，通过确定的价格和公平交易的条件，结合货币金融市场的国际会计准则，交易双方自愿进行资产交换或者债务清偿。在当前经济形势紧张和经济压力不确定的市场环境下，市场的经济指数波动对公允价值计量的精确性带来较大的影响，需要对公允价值的计量方法进行优化改进，提高对市场波动和经济序列指数的预测精确性，相关的算法研究受到人们的重视。

传统方法中，对市场波动的经济指数环境下的公允价值的计量方法主要有基于非线性经济序列分析的公允价值计量方法、基于相空间重构的公允价值计量方法、基于主成分分析的公允价值计量方法等，然而传统方法都将市场波动的经济指数序列当作是一组平稳的随机过程，对经济指数序列的非线性成分特征的利用效率不好，导致在进行公允价值计量中出现误差，无法可靠地为经济统计部门提供会计准则。对此，相关文献进行了算法改进设计，其中，文献[4]提出一种基于零冗余度模糊C均值聚类的市场波动经济下的公允价值计量方法，有效建立一个对市场经济波动下的公允价值的走势预测模型，对该区域的市场经济波动下的公允价值测量体系进行C均值聚类分析，提高了公允价值计量的准确度，但是该算法在进行线性时间序列预测时可能出现自相关误差，导致对会计分析过程产生失真，且计算开销较大。文献[5]提出一种基于支持向量机(Support Vector Machine, SVM)模型的市场经济波动预测算法，采用混沌时间序列分析方法，通过公允价值模式的转变，进一步细化和强化了对持续经营能力的评估和分析，提高了计量的可靠性，但是，该模型具有计算开销过大，在公允价值计量过程中的收敛性不好。针对上述问题，本文提出一种基于非线性经济指数序列分析和市场波动经济预测的公允价值计量方法，首先构建了市场波动经济指数的非线性序列分析模型，采用最大Lyapunov指数特征提取方法构建公允价值计量的输入参量特征，以此为基础，结合平均互信息方法构建一个状态预估计器，实现市场波动的经济预测，以此实现公允价值计量算法的改进。仿真实验进行了性能验证，展示了本文算法在提高公允价值计量准确性，改进金融利率、价格波动性、信用风险等参数的评估性能方面的优越性。

二、公允价值计量的基本原理和市场波动经济指数预测模型构建

1.公允价值计量的基本原理和算法原理介绍

随着市场经济建设的深化与金融境外流通的扩大，最终必然导致市场经济的波动。随着全新的《39号公允价值计量准则》掀开了神秘面纱，新的公允价值计量模式推出，在市场经济波动的时代背景下，《39号公允价值计量准则》是财政部针对市场经济波动推出的新的企业会计准则标准体系。市场经济波动对中国的经济和公允价值的计量带来巨大的影响，公允价值的计量模式主要采用的是价值评估模型，具体方法是建立计量日的可能交易价格，考虑资料输入的使用、可观察的市场信息，通过“公允价值变动损益”对企业利润产生影响，调整信用风险贴水，确定合理的公允价值。公允价值计量模式参考因素如图1所示。

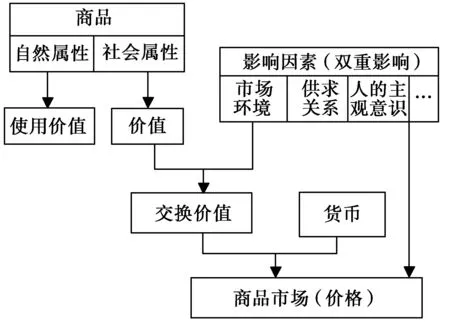
图1　公允价值计量模式参考因素

本文为了提高对市场计量的公允价值的估价准确性，提出一种基于非线性经济指数序列分析和市场波动经济预测的公允价值计量方法。为了实现对公允价值的优化计量，采用相空间重构方法，得到公允价值计量模式下的经济增长指数在多维相空间中的时间序列模型，表示为：

xi=(xi,xi+τ,L,xi+(m-1)τ)i=1,2,L,N-(m-1)τ

(1)

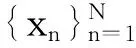
(2)

其中，公允价值计量的空间状态嵌入维数m，时间延迟τ，在计量日发生的有序交易产生的资产收益采用协方差矩阵C，表示为：

(3)

(3)式中市场经济波动下的公允价值数据的代价函数参量矩阵和矢量分别为：

l=[1,1,L 1]1×N

(4)

(5)

X=[X1,X2,L,Xm]

(6)

对公允价值计量的评估模型L进行奇异值分解L=U*S*C。结合市场的影响因素，根据市场环境、市场供求关系，可得U和C是正交矩阵，而

C=(c1,c2,L,cn)

(7)

其中S为L的奇异函数，采用奇异特征分解方法，得到公允价值计量的自相关特征的对角向量为：

S=diag(σ1,σ2,L,σn),σ1≥σ2≥L≥σn≥0

(8)

公允价值计量作为金融计量工具，估计当时价格，对预期市场进行有利推测，对公允价值计量模式设计，通过上述设计，进行公允价值计量。

2.市场波动经济指数预测模型构建

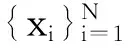
f(x)=ωT(φ)x+b

(9)

上式中，ω表示市场经济波动持续时间加权值，b表示为公允价值计量的偏差向量。采用SVM模型的训练市场波动经济指数集合，选取最小化的风险加权，对商品的自然属性和社会属性进行衡量，得到属性衡量的描述形式为：

(10)

结合市场的影响因素，根据市场环境、市场供求关系对SVM模型进行训练，使得训练具有更好的推广能力，得到市场经济波动预测优化模型为：

(11)

三、公允价值计量算法改进实现

根据上述市场波动经济预测结果，进行公允价值计量算法改进设计，采用最大Lyapunov指数特征提取方法构建公允价值计量的输入参量特征，得到市场波动经济指数序列的最大Lyapunov指数：

(12)

计算公允价值计量的输入参数向量{δxi+1(jk)=xjk+1-xi+1|k∈1,L,Nb}，在市场经济波动下，会计准则和国际准则趋同，得到又一个N×m子空间的邻域矩阵：

(13)

(14)

(15)

(16)

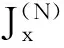
dm(0)=‖Xm-Xk‖

(17)

(17)式中，Xm和Xk进一步发展演变为Xm+1和Xk+1。纳入“综合收益”和“其他综合收益”，进行公允价值的高斯分布、特征分布，结合模型构建得：

‖Xm+1-Xk+1‖=‖Xm-Xk‖eλ1

(18)

在(18)式中，Xm+1的最末分量X(tn+1)为一个差分函数，且唯有它是未知的，采用最大Lyapunov指数分岔原理，得到公允价值计量的最优解集为：

Xm+1(m)=Xk+1(m)±

(19)

设N0=0，D0=1，在市场经济与金融国际化下，对公允价值的计量采用平均互信息法求得输入的参量集合，对k=1,2,L,n-1，φkj由下面的递推公式，实现过程收敛，其中j=1,2,L,k，递推公式为：

(20)

(21)

φkk=Nk/Dk

(22)

φkj=φk-1,j-φkk·φk-1,k-j

(23)

最后根据市场环境、市场供求关系和人的主观意识，将对所计算的结果进行取舍，谨慎使用价值评估模型，实现对公允价值的计量模式的改进。

四、仿真实验与结果分析

为了测试本文的公允价值计量方法在实现金融利率、价格波动性、信用风险参数的评估和市场波动预测中的应用性能，进行仿真实验。实验的计算机硬件配置参数为：Intel Core2 Duo1.80GHz，1G内存，主频为DDR2 667，操作系统为Windows 7。仿真实验采用NS-2.27和NS软件进行市场经济波动下的公允价值影响模型的模拟，以各类资产市场交易中的经济数据作为研究对象，最终获得市场经济波动下的公允价值有影响的6个因子，进行系统模型构建原始驱动数据，分别表示为x1，x2，…，x6，。对x1，x2，…，x66个驱动因子数据进行金融利率、价格波动性、信用风险的评估，得到原始的经济指数序列波形如图2所示。

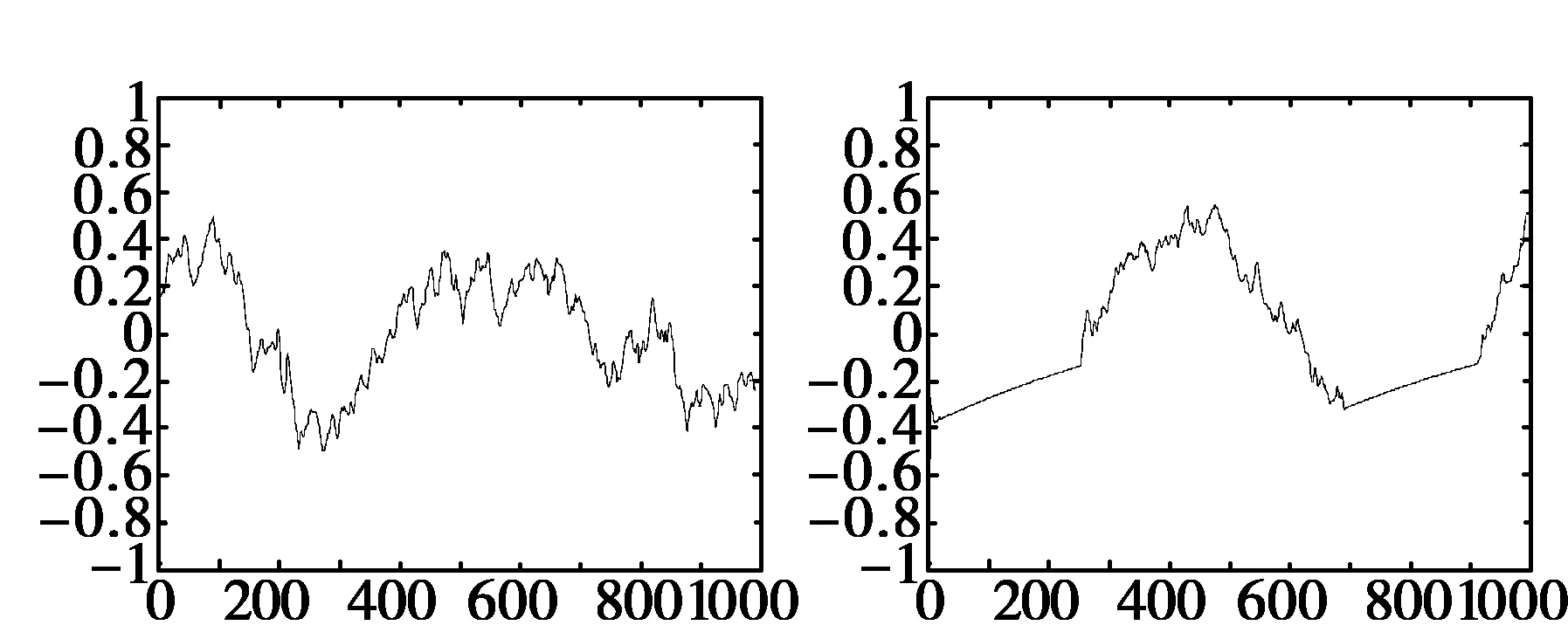
图2　6个公允价值计量驱动因子的原始经济指数采集数据波形

以上述6个公允价值计量驱动因子的原始经济指数序列为研究对象，进行市场波动预测，得到经济指数预测的归一化幅度值，如图3所示。

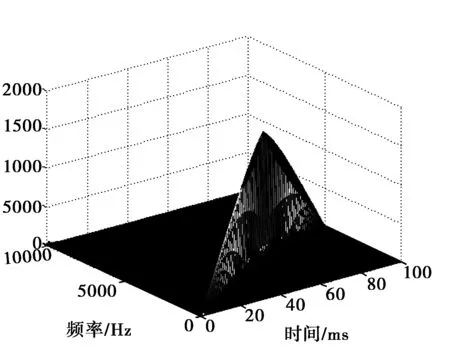
图3　市场波动预测归一化幅度

从上述结果可见，采用本文方法通过市场波动经济预测，以此实现公允价值的计量，可以提高计量的客观性和可靠性，为了对比算法性能，采用本文计算方法和传统方法，得到公允价值计量误差的对比结果如图4所示。

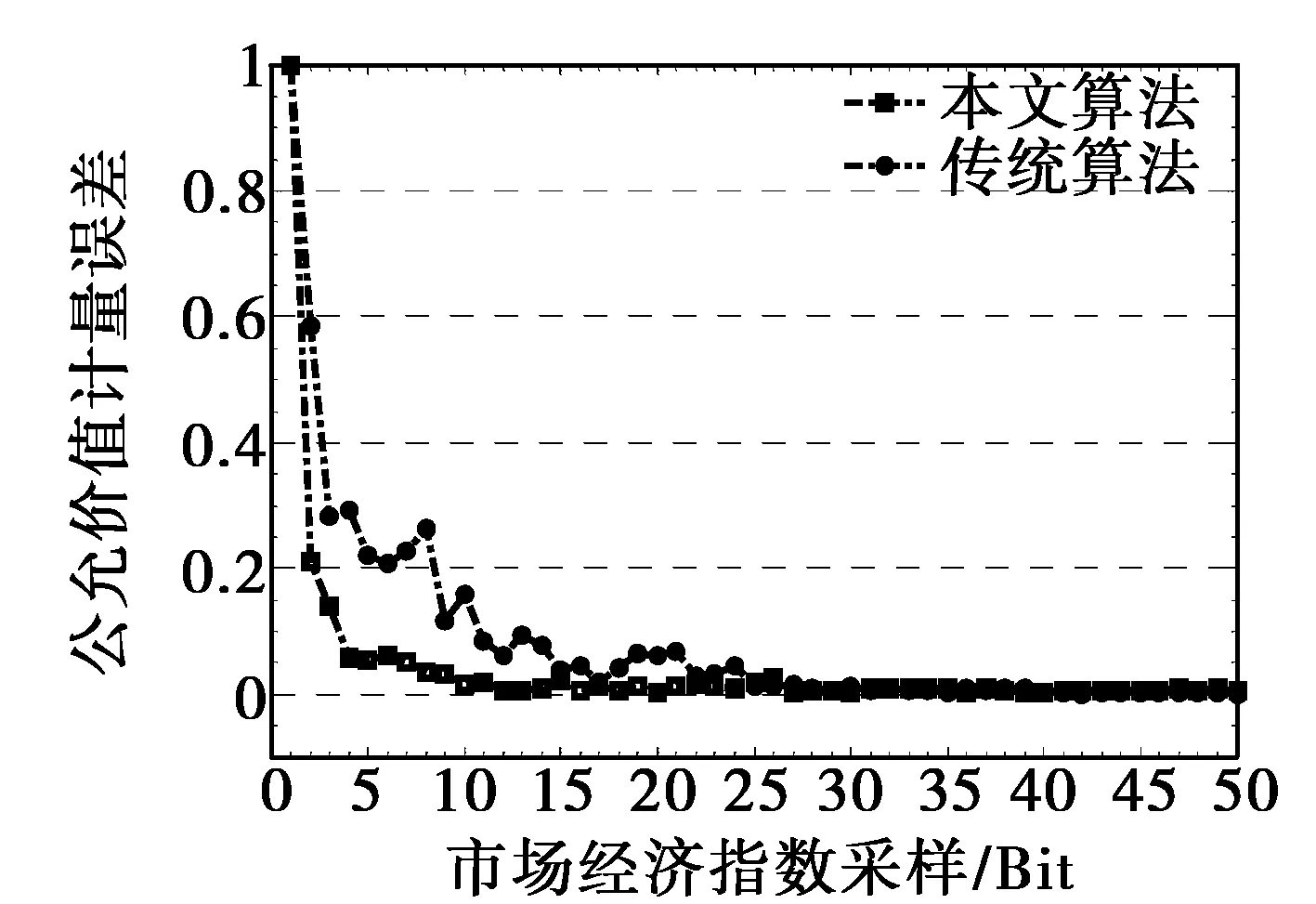
图4　公允价值计量误差对比

从图4可见，采用本文方法进行市场经济波动下的公允价值计量，误差较小，收敛性较高，实现市场波动的经济预测，对金融利率、价格波动性、信用风险等参数的评估性准确度较高，展示了较好的应用性能。通过公允价值计量，促进金融价值的信息披露，在监管过程中发挥主导性作用，通过分析、监测和评价整体市场金融体系的宏观监管，提高风险控制能力。

五、结语

为了提高对市场计量的公允价值的估价准确性，提出一种基于非线性经济指数序列分析和市场波动经济预测的公允价值计量方法。构建了市场波动经济指数的非线性序列分析模型，实现市场波动的经济预测，由此实现公允价值计量方法的改进设计。数据仿真测试结果表明，采用该算法进行市场波动经济条件下的公允价值计量和经济指数预测，具有较高的准确性，算法的收敛性和稳定性较好，精度高于传统计量方法，对金融利率、价格波动性、信用风险等参数的评估性能较高，应用价值较好。

参考文献：

[1]张普宁,刘元安,吴帆,唐碧华,吴超.物联网中适用于内容搜索的实体状态匹配预测方法[J].电子与信息学报,2015,37(12):2815-2820.

[2]SU Hongtao, LIU Hongwei, SHUI Penglang, et al. Adaptive beamforming for nonstationary HF interference cancellation in skywave over-the-horizon radar[J]. IEEE Transactions on Aerospace and Electronic Systems,2013,49(1):312-324.

[3]GENG Zhe, DENG Hai, HIMED B. Adaptive radar beamforming for interference mitigation in radar-wireless spectrum sharing[J].IEEE Signal Processing Letters,2015,22(4):484-488.

[4]YANG Yunchuan, SUN Cong, ZHAO Hui, et al. Algorithms for secrecy guarantee with null space beamforming in two-way relay networks[J].IEEE Transactions on Signal Processing,2014,62(8):2111-2126.

[5]包家龙.对FAS157公允价值计量准则的分析[J].中国乡镇企业会计，2013，(12)：20-23.

[6]王海连.国际视角下的公允价值计量研究[D].沈阳:东北财经大学,2012.

[7]黄燕飞.中国会计准则国际趋同策略研究[D].北京:财政部财政科学研究所,2012.

[8]财政部会计司编写组,编.企业会计准则讲解[M].北京：人民出版社,2010.

[9]赵彦锋,汤湘希,王昌锐,著.公允价值会计研究[M].北京：经济科学出版社,2010.

[10]徐经长,曾雪云.金融资产规模、公允价值会计与管理层过度自信[J].经济理论与经济管理,2012,(7)：41-43.

(作者单位：广州华立科技职业学院)

(责任编校：陈强，王彩红)