融合外场使用和加速寿命数据的可靠性评估方法
蔡忠义, 陈云翔, 王莉莉, 罗承昆
(空军工程大学装备管理与安全工程学院, 陕西 西安 710051)
融合外场使用和加速寿命数据的可靠性评估方法
蔡忠义, 陈云翔, 王莉莉, 罗承昆
(空军工程大学装备管理与安全工程学院, 陕西 西安 710051)
摘要:针对寿命服从双参数Weibull分布且已在外场使用一段时间后的机电产品,进行单应力、定时转换的步进加速寿命试验,研究外场使用数据和加速寿命试验数据之间的融合评估问题。考虑到外场多应力环境与实验室单一应力环境之间的差异性,构建基于修正系数的分布参数计算模型;开展融合外场使用历程和加速寿命试验过程的统计分析,建立各应力下的累计分布函数关系;构建融合过程的极大似然函数,运用数值迭代法,求解未知参数估计;结合某型机电产品进行仿真方案设计,采用蒙特卡罗仿真方法产生样本数据,通过对比分析说明本文所提出的模型评估精度更高。
关键词:加速寿命试验; 可靠性评估; 应力环境差异; 修正系数; 数据融合
0引言
随着科学技术的快速发展,机电产品的寿命与可靠性得以大幅提高并广泛应用于航空航天、机械重工、电气工程等领域。为了高效准确地评估机电产品的寿命与可靠性,在有限的试验样本和试验经费的基础上,需要采用加速寿命试验,以达到评估产品可靠性的目的[1]。
针对机电产品加速寿命试验数据的可靠性评估研究,一般思路为:假定产品寿命服从特定的分布模型(如Weibull),采用已知的加速模型,建立可靠性模型及似然估计函数,求解未知分布参数,从而外推出产品的寿命与可靠性[2-3]。目前,该领域的研究可归纳为以下:
一是应力施加方式。常见的有恒定、步进应力[4-5]。恒定应力试验设计相对简单,但所需的试验样本量较大;步进应力试验因其可以充分利用试验样本信息,节约试验时间和经费,在工程实践中得以广泛使用。就机电产品而言,步进应力加速寿命试验主要适用于高可靠长寿命、价格昂贵、技术工艺上延续前批次且不影响系统安全的产品,以确保试验风险在可控范围内。如:针对军用运输机上的起动发电机,采用步进加速寿命试验技术,开展了产品定延寿研究,为延长产品大修间隔期提供了技术支撑。
二是考虑外、内场环境差异性[6-9]。这类研究采用广义加速模型,对外场多应力进行近似折算,从总体上对分布模型参数进行修正。如:文献[8-9]在产品寿命服从Weibull场合下,针对恒定应力加速寿命试验开展研究,考虑到外场应力与试验应力之间的差异以及外场环境的复杂性,分别建立了考虑修正系数的加速模型和分布参数模型,从而外推出产品在外场使用环境下的寿命与可靠性。
三是融合多源寿命信息[10-13]。这类研究主要是采用数值迭代法或贝叶斯法来融合多源信息,建立未知分布参数的估计模型。文献[10]采用Newton-Raphson迭代法求得寿命参数的极大似然估计,这种方法利用似然估计函数自身的收敛性来近似求解未知参数,易于理解,工程应用广泛;文献[12]综合利用加速退化试验信息、加速寿命试验信息和外场信息,采用马尔可夫蒙特卡罗(Markov Chain Monte Carlo, MCMC)方法,通过判断马尔可夫链的收敛性来求解未知参数的估计值,从而外推出产品外场寿命与可靠性。这种方法的优点是可以快速完成传统似然函数的复杂求解过程,但对于未知参数先验分布的选取还需进一步探讨。
因此,本文针对寿命服从双参数Weibull分布且在外场已使用一段时间的机电产品进行单应力、定时转换的SSALT,建立考虑外场应力与环境差异的寿命分布修正模型,提出了融合外场使用和加速寿命数据的可靠性评估方法,采用数值迭代法来求解未知参数估计。
1考虑外场应力差异的寿命模型
1.1寿命模型
对于机电产品而言,一般认为其寿命服从Weibull分布,则Weibull场合下的产品寿命分布函数可表示为
(1)
式中,m为形状参数;η为尺度参数;γ为位置参数。
当γ=0时,称为双参数Weibull,此时分布密度函数和可靠度函数分别为
(2)
(3)
1.2加速模型
加速模型是指在加速试验中产品寿命特征量(如特征寿命、失效率等)与所施加的加速应力之间的关系模型,其中较为常见的是针对温度应力的Arrhenius模型和针对电应力的逆幂律模型[14]。
对于双参数Weibull,一般认为形状参数m与应力S无关,而尺度系数η与应力S有关,用特征寿命tη=η(即R(tη)=e-1)作为加速模型的特征量,则加速模型可表示为
(4)
式中,a,b是待定常数;对于Arrhenius模型,φ(S)=1/S;对于逆幂律模型,φ(S)=lnS。
1.3考虑外场应力差异的模型修正
与内场(实验室)应力环境相比,产品在外场工作环境所发生的失效机理更加复杂,通常是由多方面应力共同作用而出现的。因此,对于外场工作环境中的产品寿命分布模型应进行一定的修正。
若产品在外场工作环境中受诸如温度、电压、振动、湿度等多类型应力S,ST,SV,SM,…作用且仅有单一应力S被施加于ALT中,则基于ALT应力的加速模型可表示为

(5)
而基于外场使用环境下的多类型应力的广义加速模型可近似表示为
(6)
式中,ηf和η分别为外场工作应力和ALT单一应力下的Weibull尺度参数。
若用ln(k1)(k1为应力修正系数)来代表除S以外的其他应力的影响,即
(7)
则由式(5)~式(7)可得
(8)
则有
(9)
虽然Weibull形状参数m与应力无关,但考虑到产品组装、工艺、维护保养、管理等因素的影响,外场使用中的产品与ALT中的产品会一定差异,用环境差异系数k2来表示这种差异,即
mf=m·k2
(10)
式中,mf和m分别为外场多应力和ALT单一应力下的Weibull形状参数。
2融合外场使用和ALT的统计分析
2.1统计假设
对于开展融合外场使用数据和ALT数据统计的产品应满足以下假设:
(1)ALT采用定时截尾方式,以温度为步进试验应力,各温度Si(i=1,2,…,n)下产品寿命t之间相互独立且都服从于双参数Weibull(mi,ηi);
(2)ALT中产品失效机理保持不变,即各温度Si下Weibull的形状参数不变,令mi=m;
(3)ALT中产品满足Nelson提出的累积失效模型,即产品的剩余寿命仅与当前应力和已累计失效水平有关;
(4)ALT各温度Si下Weibull的特征寿命tηi=ηi与其温度之间满足以下加速方程:
(11)
2.2统计过程及数据
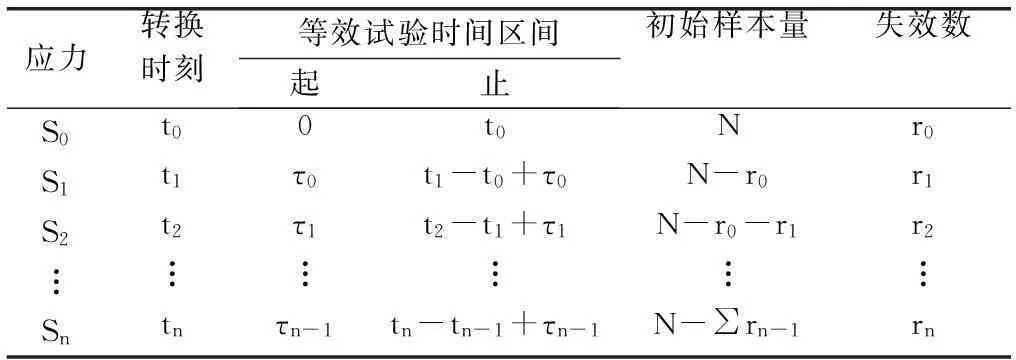
根据步进试验方案,预先确定一组高于外场正常工作温度S0的温度应力S1 假设有一批共N个产品作为样本总体,在进行SSALT前,该批产品已在外场工作了t0时刻且有r0个产品失效并记录了失效时间,可近似看作是SSALT的第一步;然后将余下未失效产品放置在温度应力S1下进行试验,到达转换时刻t1前有r1个产品失效并记录了失效时间;而后将应力提高至S2继续试验,达到转换时刻t2有r2个产品失效并记录了失效时间;而后将应力提高至下一应力,如此进行,一直到将应力提高至Sn下截止tn时刻完成试验(见图1)。 图1 考虑外场使用的步进应力施加过程 通过收集到上述整个过程的失效数据可知,各应力下的失效样本时间序列如下: 获取各应力下的数据样本后,需要进行分布检验以判断产品是否服从Weibull分布,一般采用F检验法、χ2检验法[15]。 2.3各应力下分布函数关系 已知N个产品在外场工作温度为S0下的工作时间为t0,则t0时刻的产品累计失效概率为F0(t0),相当于产品在应力S1下τ0时刻的累积失效概率F1(τ0),则考虑了外场工作历程的未失效产品在应力S1下进行试验的起止时刻为(τ0,t1-t0+τ0]。 同理,产品在应力S1下t1-t0+τ0时刻的累计失效概率为F1(t1-t0+τ0),相当于在应力S2下τ1时刻的累积失效概率F2(τ1),则未失效产品在应力S2下进行试验的起止时刻为(τ1,t2-t1+τ1]。依此递推(见表1),可建立各应力下的寿命分布函数关系,则融合了外场使用和ALT数据的累计分布函数可分步表示如下: 步骤 1外场环境下温度应力S0 (12) 式中,考虑到外场应力修正与环境差异系数,可知 (13) 式中,m0,η0为ALT应力S0下Weibull的形状参数和位置参数。 步骤 2ALT温度应力S1 (14) 式中,τ0可通过下式求出。 (15) 步骤 3ALT温度应力S2 (16) 式中,τ1可通过下式求出。 (17) 步骤 i+1ALT温度应力Si,i=1,2,…,n (18) 式中,τi-1可通过下式求出。 (19) 3寿命可靠性模型 根据融合外场使用和ALT的统计过程分析及各应力的累积分布函数关系,建立整个融合过程的极大似然函数。 (1) 外场温度应力S0下寿命数据极大似然函数为 (20) (21) (2)ALT各温度应力Si下寿命数据极大似然函数为 (22) (23) 其中 (24) (3) 融合了外场和ALT数据的产品对数似然函数可表示为 (25) (26) 4仿真实例 某型起动发电机是安装在军用飞机上为APU提供直流电源的供电装置,属于典型的机电产品。该型产品在部队外场已使用一段时间,外场使用与维护数据充足,现需要综合利用外场使用数据和ALT数据以推断出其在外场正常使用下的寿命与可靠度。 4.1仿真数据 利用蒙特卡罗仿真方法产生整个融合过程的样本数据[8],具体步骤如下: 步骤 2首先分别产生Ni(i=0,1,2)个相互独立且服从于U[0,1]的随机数;然后将其分为[0,p0)、[p0,p1)、[p1,p2)、[p2,1] 4组,分别对应于外场使用环境中样本的失效概率,ALT中加速应力S1下样本的失效概率,ALT中加速应力S2下样本的失效概率以及到截尾时样本仍未失效的概率。 步骤 3将产生的N0个随机数中落入[0,p0)内的r0个随机数U0j(j=1,2,…,r0)转换为外场使用环境下的失效样本时间为 (27) 步骤 4将产生的N1个随机数中落入[p0,p1)内的r1个随机数U1j(j=1,2,…,r1)转换为ALT中加速应力S1下失效样本时间为 (28) 步骤 5将产生的N2个随机数中落入[p1,p2)内的r2个随机数U2j(j=1,2,…,r2)转换为ALT中加速应力S2下失效样本时间为 (29) 4.2仿真方案 通过统计分析该机电产品或其同类产品在研制阶段所进行的寿命试验数据,结合经验做法,可初步推断出其寿命服从Weibull的参数值以及加速模型的参数值并作为仿真初值。具体仿真参数设置如下: (1) 外场使用:外场应力与环境修正系数分别为k1=0.9,k2=1.1,初始样本量N=20,正常工作温度S0为50oC,p0=0.1; (2)ALT:加速应力数为2,即S1=75oC、S2=100oC,p1,p2分别取0.3、0.7; (3) 加速模型:Arrhenius模型参数a、b分别为9.174、-2.248,分布模型的形状参数m=2.168; (4) 仿真次数M=100。 4.3对比分析 根据上述仿真方案所产生的外场使用与ALT样本数据,将本文所提出的融合外场使用和ALT数据且考虑了外场应力与环境差异的方法记为M1,将融合外场使用和ALT数据但未考虑外场应力与环境差异的方法记为M2,将只利用ALT数据进行评估的方法记为M3,分别推断出产品寿命指标,通过对比分析来判断各方法的拟合精度。 (1) 判断标准 依据赤池信息量准则(Akaikeinformationcriterion,AIC)和总体均方误差(totalmeansquarederror,TMSE)来判断方法的优劣[9],计算公式为 AIC=2p-2lnL(Θ) (30) 式中,p为Θ中未知参数的个数;lnL(Θ)为对数似然函数所取的极大值。 (31) (2) 参数估计 采用Newton-Raphson迭代法对式(26)进行寻优,求解不同方法下的参数估计值;根据式(30)、式(31),计算出各方法的AIC和TMSE(见表2)。由表2可知,各模型拟合的优劣程度依次为:M1优于M2,M2优于M3。 表2 不同方法的参数估计结果 (3) 评估结果 根据式(26),计算出产品在外场正常使用下的特征寿命估计值,从而绘制出各方法所得到的产品可靠度曲线(见图2)。从图中可直观看出,本文所提出的考虑了外场差异且融合了外场使用和ALT数据的评估模型精度最高,具有良好的趋势拟合性;而传统未考虑外场差异且只利用ALT数据的评估模型精度最差,主要是因其将参与ALT的样本都视为新品,忽略了外场工作历程会降低产品可靠度。 图2 不同方法的可靠度曲线 5结论 (1) 针对具有外场工作历程且寿命服从双参数Weibull的机电产品,开展SSALT,提出了融合外场使用和ALT数据的可靠性建模方法; (2) 考虑了外场应力环境的差异,采用双修正系数,对外场正常工作应力下的Weibull分布参数进行修正,使得分布模型更加符合外场实际; (3) 本文从修正寿命分布模型和扩大样本量两方面着手,所提出的方法能较好地反映产品寿命特征规律。通过与传统未考虑外场差异和未融合外场数据的模型评估结果比较,进一步说明本方法较传统方法的评估精度更优,具有良好的工程应用价值。 参考文献: [1] Zhang C H, Wen X S, Chen X. A comprehensive review of accelerated life testing[J].ActaArmanentarii, 2004, 25(4): 485-490. (张春华, 温熙森, 陈循. 加速寿命试验技术综述[J].兵工学报, 2004, 25(4): 485-490.) [2] Ding C, Yang C Y, Tse S K. Accelerated life test sampling plans for the Weibull distribution under Type I progressive interval censoring with random removals[J].JournalofStatisticalComputationandSimulation, 2010, 80(8): 903-914. [3] Zhang X P, Shang J Z, Chen Xun, et al. Statistical inference of accelerated life test with competing failures based on three-parameter weibull distribution[J].ActaArmanentarii, 2013, 34(12): 1603-1610. (张详坡, 尚建忠, 陈循, 等. 三参数Weibull分布竞争失效场合加速寿命试验统计分析[J].兵工学报, 2013, 34(12): 1603-1610.) [4] Ismail A A. Inference for a step-stress partially accelerated life test model with an adaptive Type-II progressively hybrid censored data from Weibull distribution[J].JournalofComputationalandAppliedMathematics, 2014, 260(4): 533-542. [5] Fard N, Li C H. Optimal simple step stress accelerated life test design for reliability prediction[J].JournalofStatisticalPlanningandInference, 2009, 139(1): 1799-1808. [6] Meeker W Q, Escobar L A, Hong Y L. Using accelerated life tests results to predict product field reliability[J].Technometrics, 2009, 51(2): 146-161. [7] Pan R. A Bayes approach to reliability prediction utilizing data from accelerated life tests and field failure observations[J].QualityandReliabilityEngineeringInternational, 2009, 25(2): 229-240. [8] Wang Y S, Zhang C H, Chen X, et al. Statistical analysis of accelerated life testing for products with operational period[J].JournalofNationalUniversityofDefenseTechnology, 2008, 30(1): 94-98. (汪亚顺,张春华,陈循,等.存在工作历程产品的加速寿命试验统计分析[J].国防科技大学学报,2008,30(1):94-98.) [9] Tan Y Y, Zhang C H, Chen X, et al. Remaining life evaluation based on accelerated life testing[J].JournalofMechanicalEngineering, 2010, 46(2): 150-154. (谭源源, 张春华, 陈循, 等. 基于加速寿命试验的剩余寿命评估方法[J].机械工程学报,2010,46(2):150-154.) [10] Li L, Xu W. Reliability analysis for accelerated life test based on Weibull distribution[J].SystemsEngineeringandElectronics, 2010, 32(7): 1544-1548. (李凌, 徐伟. 威布尔产品加速寿命试验的可靠性分析[J].系统工程与电子技术, 2010, 32(7): 1544-1548.) [11] Anduin E T. Bayesian estimation of mixed Weibull distributions[J].ReliabilityEngineering&SystemSafety, 2009, 94(4): 463-473. [12] Wang L Z, Jiang T M, Li X Y, et al. Lifetime evaluation method with integrated accelerated testing and field information[J].JournalofBeijingUniversityofAeronauticsandAstronautics, 2013, 39(7): 947-951. (王立志, 姜同敏, 李晓阳, 等. 融合加速试验及外场使用信息的寿命评估方法[J].北京航空航天大学学报, 2013, 39(7): 947-951.) [13] Wang L Z, Pan R, Li X Y, et al. A Bayesian reliability evaluation method with integrated accelerated degradation testing and field information[J].ReliabilityEngineeringandSystemSafety, 2013, 112(4): 38-47. [14] Jiang T M.Reliabilitytesttechnology[M]. Beijing: Beihang University Press, 2012: 194-205. (姜同敏. 可靠性试验技术[M]. 北京: 北京航空航天大学出版社, 2012: 194-205.) [15] Zhao Y.Dataanalysisofreliability[M]. Beijing: National Defense Industry Press, 2011: 103-106. (赵宇. 可靠性数据分析[M].北京: 国防工业出版社, 2011: 103-106.) 蔡忠义(1988-),男,博士研究生,主要研究方向为装备可靠性与质量管理。 E-mail:afeuczy@163.com 陈云翔(1962-),男,教授,博士,主要研究方向为装备发展论证、装备RMS。 E-mail:cyx87793@163.com 王莉莉(1982-),女,讲师,博士后,主要研究方向为装备系统工程。 E-mail:bluechase@163.com 罗承昆(1991-),男,硕士研究生,主要研究方向为装备管理与决策。 E-mail:afeulck@163.com Method on reliability assessment with integrated field using and accelerated life data CAI Zhong-yi, CHEN Yun-xiang, WANG Li-li, LUO Chen-kun (EquipmentManagement&SafetyEngineeringCollege,AirForceEngineeringUniversity,Xi’an710051,China) Abstract:Aiming at the mechanical & electrical product that its lifetime obeys to Weibull distribution and has used in field, a single-stress & time-switching step-stress accelerated life test is done to study the integrated assessment problem between field using data and accelerated life test (ALT) data. Considering the difference between field multi-stress environment and laboratory single-stress environment, a distribution parameter model with the correction factors is constructed. Statistical analysis for the integrated process of field using and the ALT is done. Its cumulative distribution function relationship under each stress is built. The maximum likelihood function of integrated filed using and ALT data is built. The data iteration method is used to determine the estimation value of unknown parameters. A certain mechanical & electrical product is used to design a simulation project. The sample data is obtained by Monte Carlo simulation. A contrastive analysis shows that the proposed model is more accurate. Keywords:accelerated life test (ALT); reliability assessment; stress environment difference; correction factor; data integration 收稿日期:2015-04-14;修回日期:2015-09-05;网络优先出版日期:2015-12-23。 基金项目:总装“十二五”国防预先研究项目资助课题 中图分类号:TB 114.3 文献标志码:A DOI:10.3969/j.issn.1001-506X.2016.06.39 作者简介: 网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20151223.1116.032.html