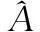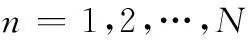基于CPT和RPF的空中高机动目标检测与参数估计

李　海, 周　盟, 吴仁彪

(1. 中国民航大学天津市智能信号与图像处理重点实验室, 天津 300300;2. 澳大利亚伍伦贡大学电气计算机与通信工程学院, 澳大利亚 伍伦贡 999029)



基于CPT和RPF的空中高机动目标检测与参数估计

李海1,2, 周盟1, 吴仁彪1

(1. 中国民航大学天津市智能信号与图像处理重点实验室, 天津 300300;2. 澳大利亚伍伦贡大学电气计算机与通信工程学院, 澳大利亚 伍伦贡 999029)

摘要：提出了一种基于三次相位变换(cubic phase transform,CPT)和重构相位函数(reconstructing phase function,RPF)的空中高机动目标参数估计方法。为了实现目标高阶参数的估计,该方法首先通过双线性变换求得接收信号的相位函数,实现信号降阶和待估参数的分离;然后利用多阵元采样重构参考阵元的相位函数,等效增加了参考阵元相位函数的时间采样,实现了参考相位函数的相干积累;最后进行参数估计。仿真结果表明,在输入信噪比较低、采样脉冲较少的情况下,该算法能够以较高的精度实现对高机动目标的参数估计。

关键词：高机动目标; 三次相位变换; 重构相位函数; 相干积累; 空时自适应处理

0引言

机载相控阵雷达以飞机为载体,机动性高、生存力强,相较地基雷达,其可视范围远,可担任警戒、指挥等重要任务,在现代战争中的作用越来越重要[1]。当雷达处于下视状态时,目标信号通常淹没在杂波背景中[2],由于杂波信号功率远大于目标信号功率,因而严重影响了雷达对目标信号的检测。相比于单天线雷达,相控阵雷达通过多通道接收目标信号,在目标信号中引入了空间信息,通过空时二维滤波,能够更加有效地抑制地杂波。空时自适应处理[3](space-time adaptive processing,STAP)技术经过几十年的发展,已成为应用在该领域的关键性技术。随着航空航天技术的不断发展,空中来袭目标的机动性越来越高,此时用速度及加速度并不能准确描述目标运动状态,需要引入更高阶的运动参数—急动度[4-5]来实现对高机动目标的精确描述。和机动性较低的目标相比,高机动目标的回波非平稳,多普勒走动较为严重,传统STAP的目标回波平稳的假设不再成立,使用传统STAP技术处理高机动目标检测问题性能不佳[3],因此对高机动目标检测和参数估计方法的研究具有重要意义。

当目标做匀急动度运动时,目标回波信号具有三次相位信号(cubic phase signal,CPS)[6]形式。近年来,各种针对CPS信号的参数估计方法不断出现,包括最大似然方法、离散多项式相位变换[7-9]、空间采样重构时间采样法、三次相位变换(cubic phase transform,CPT)[10-14]等。最大似然法理论效果最优,该方法采用搜索的方式对信号进行检测,其运算复杂度随着信号的阶数剧烈上升,直接使用该方法解决三次相位信号问题,其运算复杂度将已立方为计,不利于实际系统的实现。离散多项式相位变换对信号进行四阶非线性变换,实现了对三次相位信号参数的精确估计,但是该方法对采样脉冲数和信噪比门限的要求较高[7]。CPT提出的应用背景是用于解决信号瞬时频率变化率(instantaneous frequency rate,IFR)[6,15]的估计问题,该方法只对信号进行二阶非线性变换,对采样脉冲数和信噪比门限的要求较离散多项式相位变换方法低。但是受到机载预警雷达采样脉冲数较少的限制,CPT方法仍然难以得到直接运用。空间采样重构时间采样法[16-18],能够在采样脉冲数较少的情况下提供较高的参数估计精度,但是由于该方法对三阶信号重构运算量,将其直接运用到三阶参数估计问题中运算量较大。本文提出了一种基于CPT和重构相位函数(reconstructing phase function,RPF)的高机动目标参数估计方法,该方法通过双线性变换求得接收信号的相位函数矩阵,实现信号降阶和待估参数的分离;然后利用空间采样重构参考阵元的相位函数,实现相位函数的相干积累;最后以搜索方式估计高机动目标运动参数。本文将所提算法与CRB界及传统方法进行了比较。结果证明,在输入信噪比较低、采样脉冲数较少的情况下,本文方法能够较为准确的估计目标参数。

1信号模型和问题描述

本节介绍高机动目标回波模型。如图1所示,设机载平台沿航向方向放置均匀线阵,阵元数为N,相干处理脉冲数为K,阵元间距为d=0.5λ,其中λ为雷达发射脉冲的波长。

对于急动度不变的高机动目标,其在慢时间k时刻与雷达平台的距离为目标在初始时刻与雷达平台的距离Ro及由于目标运动产生的距离增量ΔR(k):

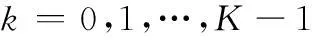
(1)

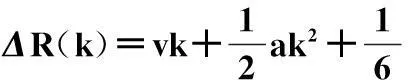
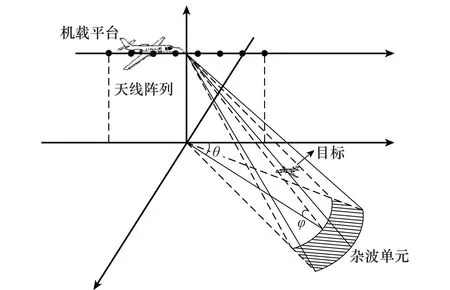
图1　雷达与杂波散射单元几何模型

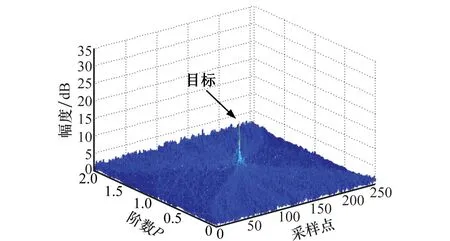
在暂不考虑距离走动的情况下,对于第n(n=1,2,…,N)个阵元,在k时刻其接收的目标回波信号可以表示为

(2)

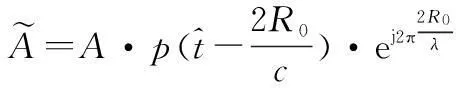
(3)

为了方便表示,令β1=4πv/λ、β2=2πa/λ、β3=2πja/3λ,则时间相位φtk可表示为

(4)

由式(3)可以看出:

(1) 对于雷达的接收信号,其空间相位φsn只与阵列结构(阵元数n及阵元间距d)及信号来向有关;

(2) 在目标运动参数一定的情况下,时间相位φtk仅由采样时刻决定,与阵元结构(阵元数n及阵元间距d)无关,并且为采样时刻k的三次函数。

由此可知,相控阵体制下,各阵元接收的匀急动度运动目标的回波信号为附带了不同空间相位(不同阵元的空间相位不同)的三次相位信号。雷达接收的待检测单元目标的回波可以表示为

(5)

则待检测单元的空时快拍数据[3]为

(6)

式中,c和n分别表示杂波和噪声。

2基于CPT和RPF的高机动目标参数估计方法

CPT最早应用在对信号的瞬时频率变化率的估计问题上,经过发展成为一种有效的三次相位参数估计方法。它通过双线性变换将三次相位信号转化为信号的相位函数,实现对信号IRF的估计;然后通过估计两个特定时刻的IRF,以解线性方程组的形式实现原三次相位信号的参数估计[6]。由于CPT方法实现三阶参数估计需要较多的样本,无法直接应用到机载相控阵预警雷达中。本文提出的基于CPT和重构相位函数的高机动目标参数估计方法首先对杂波抑制后的接收信号进行双线性变换获得信号的相位函数,实现信号降阶和待估参数分离,然后通过重构相位函数,将多阵元短的相位函数重构成为参考阵元长的相位函数,实现相干积累,最后进行参数估计。

2.1双线性变换

对于第n个阵元的接收信号srn(k),定义其瞬时频率变化率为

(7)

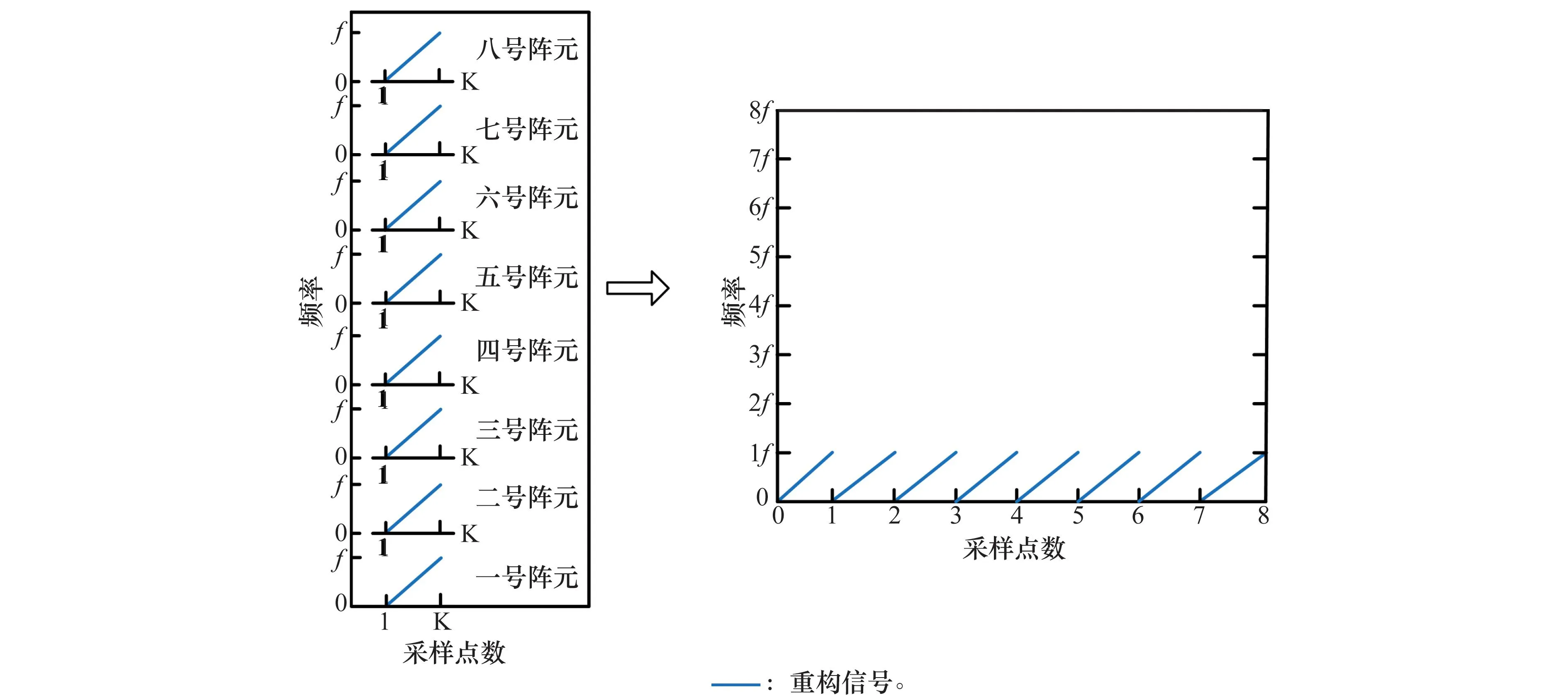
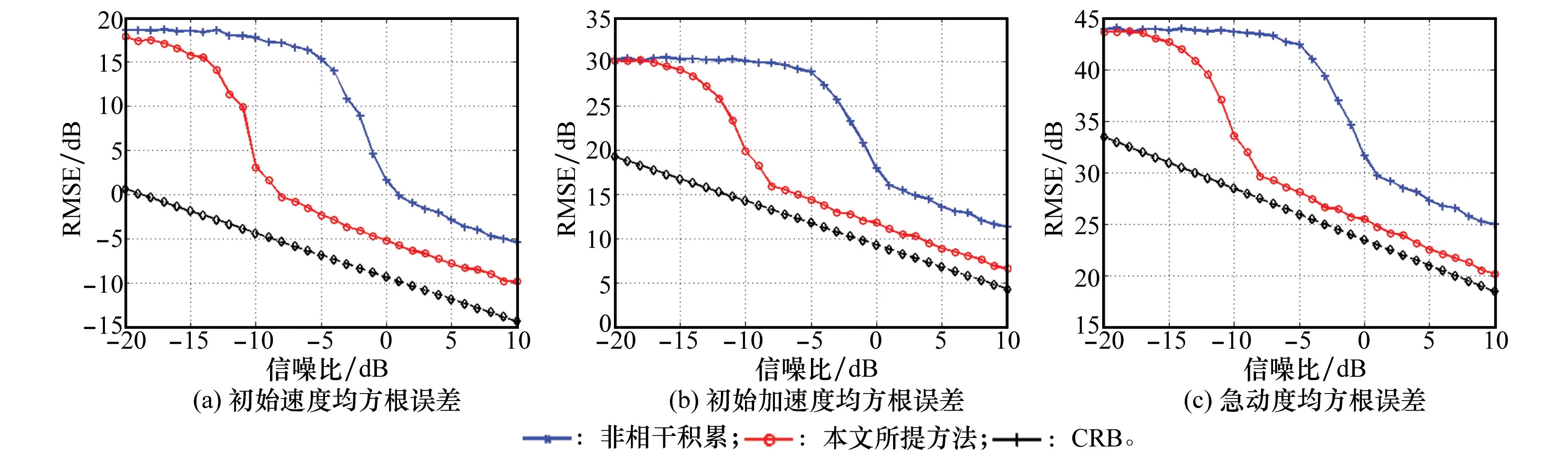
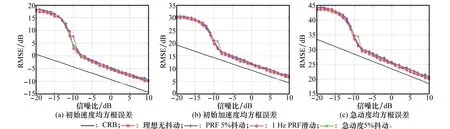
可以看出,瞬时频率变化率是原信号二阶、三阶参数β2、β3的线性组合。本文通过在κ(0<κ

(8)

式中

(9)

(10)

(11)

由式(8)可以看出，pn κ(τ)为自变量为τ的二次相位信号。亦即经过双线性变换,三次相位信号srn(k)被降阶成二次相位信号pn κ(τ),其自变量为变换延迟τ,参数为瞬时频率变化率Ωκ,而Ωκ只与β2、β3有关,与β1无关,因而实现了运动参数的分离。

在κ时刻,对每个阵元接收的目标信号srn(k)进行双线性变换,得到κ时刻雷达接收的目标信号的相位函数矩阵D,其表达式为

(12)

式中

(13)

(14)

式中,pcn κ(n=1,…,N)是与空间相位无关的关于变换延迟τ的二次相位函数；Φs为空间相位对角矩阵。

2.2重构相位函数[16]

由式(12)可知,各阵元目标的相位函数pn κ(τ)具有二次相位信号形式,并且不同阵元之间的相位函数只相差一定的空间相位。由式(2)可知,运动参数引起的多普勒展宽仅体现在时间相位上,与空间相位无关,本文采用文献[18]的方法对空间相位进行补偿(本文以1号阵元为参考阵元进行补偿),补偿后的相位函数矩阵为

(15)

式中，Dc表示补偿空间相位后的相位函数矩阵。由式(13)、式(15)可见,补偿空间相位后,不同阵元间的相位函数相同,其时频图如图2所示。可以看出,各阵元的相位函数的时频图相同,但由于不同阵元间相位不连续,无法直接进行相干积累。此时对每个阵元的相位函数分别进行分数阶傅里叶变换(fractional Fourier transform,FrFT),再进行非相干积累,其效果如图3所示(信噪比=0 dB)。可以看出,在脉冲数较少的情况下,非相干积累无法利用各阵元相位函数的相位信息,目标能量积累效果较差。

图2　重构前8阵元接收信号相位函数时频图

图3　重构前8阵元接收信号相位函数非相干积累图

对单个阵元来说,其接收信号采样脉冲数越多,采样时间越长,其能量积累效果越好。基于此,重构相位函数法以某一阵元接收目标信号的相位函数为参考,补偿其他各阵元目标相位函数的时间相位,然后进行拼接(即用空间采样代替时间采样),将多阵元采样脉冲少、相位不连续的相位函数,重构成为参考阵元采样脉冲多、相位连续的相位函数,使得多阵元接收信号相位函数能够进行相干积累。重构的参考阵元的目标相位函数时频图、能量积累图分别如图4和图5所示(信噪比=0dB)。由图4、图5可见,重构后的相位函数相位连续,因此能够实现多阵元相位函数的相干积累,使得能量积累效果大大提升。

图4　重构后8阵元接收信号相位函数时频图

图5　重构后8阵元接收信号相位函数相干积累图

为了讨论方便,下面以两阵元为例,讨论如何重构接收信号的相位函数。设在κ时刻两阵元接收信号的相位函数矩阵为Dc,其表达式为

(16)

式中

(17)

其中,pc1κ、pc2κ分别对应1号及2号阵元接收信号的相位函数。利用两个阵元重构后的参考阵元相位函数[16]可表示为

(18)

式中,prcp表示重构所得相位函数；⊙为Hadamard积；Δφ2为重构时2号阵元所需补偿的相位,可表示为

(19)

可以看出,补偿pc2κ时间相位后再跟pc1κ拼接,等效为增加了pc1κ的时间采样点数。当阵元数增加到N时,重构相位函数的表达式为

(20)

式中

(21)

2.3构造代价函数

上述方法在补偿时间相位Δφn中,需要使用信号瞬时频率变化率Ωκ作为重构参数。由式(10)可知,由于目标运动参数未知,Ωκ实际是未知的,这使得无法直接利用各阵元的相位函数进行重构。文献[16]指出,当补偿的瞬时频率变化率为Ωκ,重构的相位函数积累能量最大。因此构造代价函数对Ω进行估计

(22)

式中,prcp(Ω)表示以Ω为重构参数对接收信号进行重构相位函数运算；ZFP[·]表示FrFT算子。

2.4运动参数估计

(23)

由式(23)可得

(24)

(25)

再由式(3)中参数转换关系,求解高机动目标的运动参数估计值为

(26)

2.5算法流程

本文提出的基于CPT和RPF的空中高机动目标参数估计的方法流程如图6所示。

图6　本文方法实现框图

步骤 1杂波抑制[21]。本文通过将待检测的接收数据投影到由各距离单元接收信号训练所得的杂波子空间的正交子空间中,实现杂波白化,得到杂波抑制后的回波数据。

步骤 2各阵元接收信号双线性变换。选取两个特定时刻κ1和κ2,按式(8)对接收数据进行双线性变换,相位函数矩阵D1和D2。

3仿真分析

仿真参数设置:天线为正侧视理想均匀线阵,阵元数N=8,阵元间距为半波长。载机速度120m/s,平台高度10km,雷达工作波长0.32m/s,雷达快时间采样频率为2MHz,脉冲重复频率1 500Hz,相干处理脉冲数K=128,输入信噪比SNR=0dB,杂噪比CNR=50dB。高机动目标处于方位角60°处,初始速度20.1m/s,加速度99.1m/s2,急动度40.1m/s3,蒙特卡罗实验次数为400次。

图7为利用文中方法进行杂波抑制后的空时二维谱,可以看出,将接收信号向杂波子空间的正交子空间投影后,在原杂波处形成了较深的凹口,使得杂波得到了有效的抑制。但同时可以看出,由于目标机动性高,其多普勒展宽较为严重。

图7　杂波抑制后的功率谱

图9为不同方法得到的各阶参数估计值的均方根误差与CRB界随信噪比变化的曲线图。蓝色星形线表示传统CPT方法非相干积累方法的估计性能曲线,红色圆圈线表示本文方法的估计性能曲线。从仿真结果可知,本文方法能够更加精确的实现对目标参数的估计。

上述讨论建立在目标运动参数恒定、雷达工作状态理想稳定的情况下的。实际情况中,由于各种因素,并不能保证目标运动参数以及雷达工作参数完全稳定。其具体表现为目标运动中参数存在抖动起伏、雷达PRF存在抖动、雷达PRF存在滑变等情况。为了进一步说明所提算法的性能,本文对上述几种情况进行了仿真验证,其结果图如图10所示。

图8　补偿急动度、加速度后的信号频谱

图9　目标参数均方根误差随信噪比变化曲线

图10　目标参数均方根误差随信噪比变化曲线

图10中,星型线表示目标急动度在真值附近有5%随机起伏情况下,所提算法估计得到的目标参数均方根误差随信噪比变化曲线图。可以看出,目标急动度随机起伏对所提算法估计结果影响较小。

十字线为雷达PRF存在10 Hz随机抖动时,目标参数均方根误差随信噪比变化曲线图,可以看出,当脉冲重复频率存在10 Hz随机抖动时(实际情况中,现代雷达的频率稳定度在10-5量级左右,在文本仿真参数设置中,选择的10 Hz抖动量所占量级约为10-3左右,属于抖动量较大、较为恶劣的情况),所提算法依然能够较精确地实现机动目标参数估计。

菱形线为当雷达PRF存在+1Hz滑动时,目标参数均方根误差随信噪比变化曲线图,可以看出当脉冲重复频率存在的滑动量为+1 Hz时(实际情况中,现代雷达的频率稳定度在10-5量级左右,本文仿真参数中,1 Hz的频率滑动所占量级约为10-3,并且随着采样脉冲数的逐渐增加,其累积滑动量增加无法消除,属于滑动量较大、较为恶劣的情况,属于滑动量较大、较为恶劣的情况),所提算法的参数估计精度受到的影响较小。

4结论

(1) 本文主要研究了高机动目标的参数估计问题,所提方法利用CPT方法思想,实现信号的参数分离,因此能够以较低的运算量实现高机动目标的运动参数估计。

(2) 所提方法由于采用了重构相位函数技术,以空间采样代替时间采样,因而能在一个CPI内雷达发射脉冲有限的情况下,获得较为精确的参数估计结果。

(3) 通过仿真实现并与CRB界及传统方法估计性能进行了比较,可以看出,所提方法能更好的逼近CRB界,在低信噪比下优势更加明显。

参考文献：

[1] Zhang W. Analysis on airborne MIMO radar space time signal processing.[D]. Chengdu: University of Electronic Science and Technology of China, 2013. (张伟. 机载MIMO雷达空时信号处理研究[D]. 成都: 电子科技大学, 2013.)

[2] Klemm R.Principleofspace-timeadaptiveprocessing[M]. 3rd ed.UK：IET Publishers, 2006:1-133.

[3] Wang Y L, Peng Y N.Space-timeadaptiveprocessing[M].Beijing: Tsinghua University Press, 2000:1-57. (王永良,彭应宁. 空时自适应信号处理[M]. 北京:清华大学出版社,2000:1-57.)

[4] Wang Y, Li Q, Wang J. Research on maneuvering model algorithm based on vehicle tracking[C]∥Proc.oftheIEEEWorkshoponElectronics,ComputerandApplications, 2014: 585-588.

[5] Li X, Cui G, Kong L. High speed maneuvering target detection based on joint keystone transform and CP function[C]∥Proc.oftheRadarConference,2014:436-440.

[6] O’Shea P. A fast algorithm for estimating the parameters of a quadratic FM signal[J].IEEETrans.onSignalProcessing, 2004, 52(2): 385-393.

[7] Shimon P, Benjamin F. Discrete polynomial phase transform[J].IEEETrans.onSignalProcessing, 1995, 43(8): 1910-1914.

[8] Wu Y T, Hing C S, Liu H Q. Sub-based algorithm for parameter estimation of ploynomial phase signals[J].IEEETrans.onSignalProcessing, 2008, 56(10): 4977-4983.

[9] Shimon P. Estimation and detection with the discrete polynomial phase transform[D]. Davis:University of California,1993.

[10] O’Shea P. A new technique for estimating instantaneous frequency rate[J].IEEESignalProcessingLetters, 2002, 9(2): 251-252.

[11] You W, He Z S, Hu J F. et al. A movement compensation algorithm for maneuvering target in skywave radar[J].ModernRadar,2013,35(11):26-29.(游伟,何子述,胡进峰,等.一种天波雷达机动目标运动补偿算法[J].现代雷达,2013, 35(11): 26-29.)

[12] Zheng J, Su T, Liu Q H, et al. Fast parameter estimation algorithm for cubic phase signal based on quantifying effects of Doppler frequency shift[J].ProgressinElectromagneticsResearch, 2013, 142(5): 57-74.

[13] Wang P, Yang J Y. Parameter estimation of multicomponent quadratic FM signals using computationally efficient Randon-CPF[C]∥Proc.oftheEuropeanSignalProcessingConference,2006:4-8.

[14] McKilliam R, Pollok A. On the Cramer-Rao bound for polynomial phasesignals[J].SignalProcessing,2014,95(1):27-31.

[15] Orovic I, Stankovic S, Thayaparan T. Time-frequency-based instantaneous frequency estimation of sparse signals from incomplete set of samples[J].SignalProcessing, 2014, 8(3): 239-245.

[16] Wu R B, Wang X H, Li H, et al. Detection and parameter estimation of air maneuvering targets via reconstructing time samples[J].JournalofElectronics&InformationTechnology,2012, 34(4): 936-942. (吴仁彪,王小寒,李海,等.基于重构时间采样的空中机动目标检测与参数估计[J].电子与信息学报,2012,34(4):936-942.)

[17] Li H, Wang X H, Wu R B. Detection and parameter estimation of multicomponent air maneuvering targets via RELAX[J].AeronauticaetAstronauticaSinica, 2013, 34(4): 873-881. (李海,王小寒,吴仁彪. 基于RELAX的空中多机动目标检测与参数估计[J]. 航空学报, 2013, 34(4): 873-881.)

[18] Zhou F.Study of motion compensation, narrow band interference suppression and single channel GMIT of airborne SAR[D]. Xi’an: Xidian University, 2007.(周峰. 机载SAR运动补偿和窄带干扰抑制及其单通道GMTI的研究[D].西安:西安电子科技大学,2007.)

[19] Zhang X H. Detection and parameter estimation of polynomial phase signal[D]. Chengdu: University of electronic science and technology of China, 2011.(张希会.多项式相位信号的检测与参数估计[D]. 成都: 电子科技大学, 2011.)

[20] Pham D S, Zoubir A M. Analysis of multicomponent polynomial phase signals[J].IEEETrans.onSignalProcessing, 2007, 55(1): 56-64

[21] Wu R B, Jia Q Q, Li H. Detection of fast moving dim targets on airborne radar via STAP[J].JournalofElectronics&InformationTechnology,2011, 33(6): 1459-1464. (吴仁彪, 贾琼琼, 李海.机载雷达高速空中微弱动目标检测新方法[J]. 电子与信息学报, 2011, 33(6):1459-1464.)

李海(1976-),男,副教授,博士,主要研究方向为机载气象雷达信号处理、自适应信号处理、动目标检测、干涉合成孔径雷达信号处理。

E-mail:haili@cauc.edu.cn

周盟(1988-),男,硕士研究生,主要研究方向为空时自适应信号处理、动目标检测。

E-mail:bard_belief@hotmail.com

吴仁彪(1966-),男,教授,博士后,主要研究方向为自适应阵列信号处理、空时自适应处理、探地雷达信号处理。

E-mail:rbwu@vip.163.com

Detection and parameter estimation of air highly maneuvering targets via CPT and RPF

LI Hai1,2, ZHOU Meng1, WU Ren-biao1

(1.TianjinKeyLabforAdvancedSignalProcessing,CivilAviationUniversityofChina,Tianjin300300,China; 2.SchoolofElectrical,ComputerandTelecommunicationsEngineering,UniversityofWollongong,Wollongong999029)

Abstract:For the detection and parameter estimation of the air highly maneuvering targets, a new algorithm is proposed, which combines the cubic phase transform (CPT) with the reconstructing phase function (RPF). First, the bilinear transform is used to obtain the phase function matrix of the array signal,which leds to the signal reduction and estimated parameters segregation. Then, by compensating the spatial phase of the phase function matrix based on the array manifold and reconstructing the phase function based on the time phase relevance of the phase function of each array signal, a phase continuous phase function which is rich in sampling pulses is obtained. The proposed method is equivalent to increasing coherent accumulative time of the signal. In the condition of low signal-to-noise and few sampling pulses, this method can achieve good parameter estimation results. Numerical examples are provided to demonstrate the performance of the proposed algorithm.

Keywords:highly maneuvering targets; cubic phase transform; reconstructing phase function; coherent integration; space time adaptive processing (STAP)

收稿日期：2015-06-19；修回日期：2015-11-16；网络优先出版日期：2016-01-07。

基金项目：国家自然科学基金 (61471365, 61571442, 61231017)；中央高校基本科研业务费专项资金(3122015B002,Y15-12);中国民航大学蓝天青年学者培养经费资助课题

中图分类号：TN 957.51

文献标志码：A

DOI:10.3969/j.issn.1001-506X.2016.06.03

作者简介：

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20160107.0919.002.html