带自适应精英扰动及惯性权重的反向粒子群优化算法

董文永，康岚兰,2，刘宇航，李康顺

(1.武汉大学计算机学院，湖北 武汉 430072；2.江西理工大学应用科学学院，江西 赣州 341000;3.华南农业大学信息学院，广东 广州 510642)

DONG Wen-yong1,KANG Lan-lan1,2,LIU Yu-hang1,LI Kang-shun3

(1.Computer School,Wuhan University,Wuhan 430072,China;2.Faculty of Applied Science,Jiangxi University of Science and Technology,Ganzhou 341000,China;3.College of Information,South China Agricultural University,Guangzhou 510642,China)

带自适应精英扰动及惯性权重的反向粒子群优化算法

董文永1，康岚兰1,2，刘宇航1，李康顺3

(1.武汉大学计算机学院，湖北 武汉 430072；2.江西理工大学应用科学学院，江西 赣州 341000;3.华南农业大学信息学院，广东 广州 510642)

针对反向粒子群优化算法存在的易陷入局部最优、计算开销大等问题，提出了一种带自适应精英粒子变异及非线性惯性权重的反向粒子群优化算法（OPSO-AEM&NIW），来克服该算法的不足。OPSO-AEM&NIW算法在一般性反向学习方法的基础上，利用粒子适应度比重等信息，引入了非线性的自适应惯性权重（NIW）调整各个粒子的活跃程度，继而加速算法的收敛过程。为避免粒子陷入局部最优解而导致搜索停滞现象的发生，提出了自适应精英变异策略（AEM）来增大搜索范围，结合精英粒子的反向搜索能力，达到跳出局部最优解的目的。上述2种机制的结合，可以有效克服反向粒子群算法的探索与开发的矛盾。实验结果表明，与主流反向粒子群优化算法相比，OPSO-AEM&NIW算法无论是在计算精度还是计算开销上均具有较强的竞争能力。

一般性反向学习；粒子群优化；自适应精英变异；非线性惯性权重

1 引言

粒子群优化算法(PSO,particle swarm optimization)是一种基于群体进化的随机仿生优化算法，由Kennedy和Eberhart等[1]于1995年提出，其思想源于对鱼群及鸟类等群体觅食行为的模拟。算法自提出以来，由于其概念简单且易于理解和实现，在解决复杂优化问题，如非线性、多峰等问题性能表现突出，从而吸引了大批科研人员对其展开研究。目前，PSO已成功应用于交通、制造、通信工程、国防等多个不同学科及工程领域[2～4]，并取得了良好的效果。

传统PSO自提出以来，存在着几个天然缺陷，如参数依赖过大、局部搜索能力不足且易陷入局部最优、搜索精度低等。因此，大量科研人员从参数设置、自适应调整、算法混合或融合等多个角度对传统PSO进行改良。PSO中每个粒子通过一个简单的运动向量公式来控制其飞行方向，该运动向量公式主要由3个关键参数控制：惯性权重(w)、认知学习因子(c1)与社会学习因子(c2)。因此，如何控制惯性大小、设定参数，如何更好地获取搜索环境的有效信息，避免粒子陷入局部最优的同时加快算法收敛速度是改进传统PSO的关键。

本文提出了一种带自适应精英扰动及惯性权重的反向粒子群优化算法(OPSO-AEM&NIW,opposition-based PSO with adaptive elite mutation and nonlinear inertia weight)。OPSO-AEM&NIW算法取当前全局最优位(gbest)为精英粒子，将针对精英粒子的自适应变异策略(AEM)融入到反向学习中，使各粒子的自身历史最优位(pbest)趋向收敛于精英粒子(gbest)时，依据粒子的聚集程度，自适应产生变异位，从而帮助粒子跳出局部最优。同时，为加快算法的收敛，一种非线性动态惯性权重策略(NIW)被引入到新算法中，该策略使惯性权重随着粒子适应度值的变化而自适应改变。本文将新算法与多种基于反向学习PSO算法在14个典型测试函数上进行数值实验，实验结果表明OPSO-AEM&NIW算法在大部分测试函数上取得最优解的同时，收敛速度得到了显著的提高。

2 相关工作

2.1 基本PSO

PSO算法是仿生算法家族中的又一种群智能随机搜索算法，群体中个体被看作是搜索空间中没有质量和体积的粒子，每个粒子表征问题的一个候选解，具有速度与位置2个特征。在解空间中，粒子以一定的速度向自身历史最优位与全局最优位运动，不断进化候选解。

设群体在D维空间中包含N个粒子，第i个粒子在第j维的速度分量vi,j和位置分量xi,j在t+1时刻的更新式如下[5]

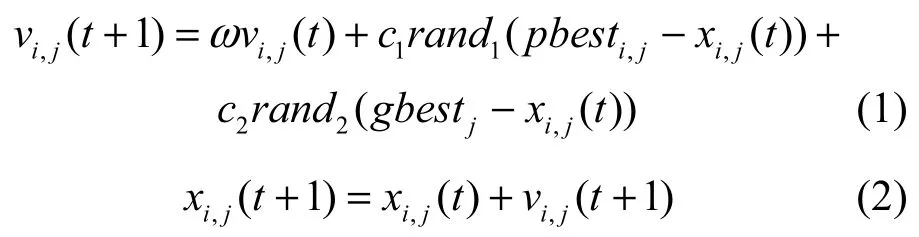
其中，i=1,2,…,N,j=1,2,…,D，ω是惯性权值，ω∈[0,1]，c1和c2分别称为认知学习因子和社会学习因子，通常，c1,c2∈[0,2]，rand1和rand2是在[0,1]上服从均匀分布的2个随机数。

2.2 一般化的反向学习策略

2005年，Tizhoosh[6]首次提出了反向学习(OBL,opposition-based learning)的概念。其主要思想是同时评估一个可行解与其反向解，将其中较优解保留，进入下一代进化。设是粒子xj的反向解，则为

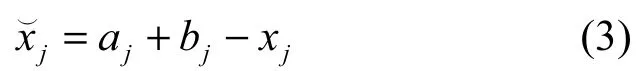
其中，xj的范围为[aj,bj]。依据概率论，解空间中个体反向解等概率优于原粒子，如对原粒子解与其反向解所构造的解空间同时进行搜索，将大大提高最优解的搜索效率。

2007年，Wang等[7]将OBL应用到PSO中，提出了一种基于OBL的PSO算法(OPSO)。2011年，Wang等在OBL的基础上进一步提出了一般性反向学习(GOBL,generalized OBL)的概念，在GOBL基础上提出了一种改进的反向学习粒子群算法GOPSO[8]。2013年，周新宇等[9]将精英思想引入到反向学习中，提出了精英反向粒子群算法(EOPSO)，该算法取群体中每个粒子的pbest作为精英粒子群，求其每一位的反向解，在其与原粒子群合并空间中选取适应值最优的前N个粒子进入下一次迭代中。同时，对当前全局最优位采用了差分变异(DEM,differential evolutionary mutation)进行扰动。为防止粒子越出搜索区域，文献[10]采用一种速度阀(velocity clamping)来控制粒子速度大小，从而进一步平衡算法的全局搜索与局部探测能力。Kaucic[11]针对边界约束问题提出了一种自适应速度的多始发反向粒子群优化算法(MSOPSOAV)，算法设计了一个基于差分操作的自适应速度更新公式来加强粒子优化能力，并采用一个超反向原则(super-opposition paradigm)对出现早熟的粒子重新初始化。Pehlivanoglu在文献[12]中提出了一种多频振动PSO算法。该算法通过一种周期性变异策略，结合人工神经网络方法保持了种群多样性，从而有效防止早熟现象的发生，使算法收敛速度得到大大的提高。基于参数的控制对进化算法的重要性，文献[13]在2015年对进化算法中参数的控制方法、趋势及挑战做出了综合性的讨论。接下来，给出一般反向学习的定义。

定义1一般反向学习策略(GOBL,generalized opposition-based learning)[8,14]。设是D维空间中的一个普通粒子，其对应的反向解为，每一维定义为

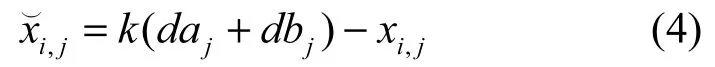
其中，k∈U(0,1)的随机数，该设定使粒子获得更好的反向解[9]，xi,j∈[aj,bj]，[daj,dbj]为第j维搜索空间的动态范围，取值为

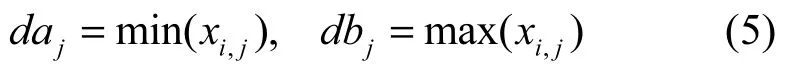
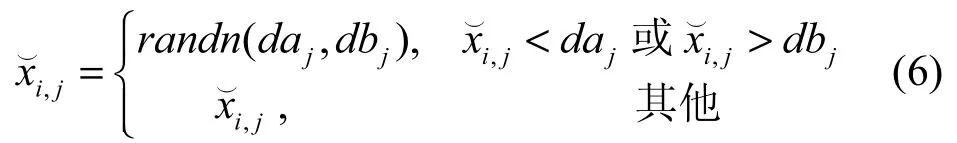
依据演化算法收敛性理论，为增强算法的顽健性，randn(daj,dbj)取在动态边界[daj,dbj]上服从高斯分布的随机数。这一设定在实验过程已被验证取得了较好的算法稳定性。高斯分布函数定义为

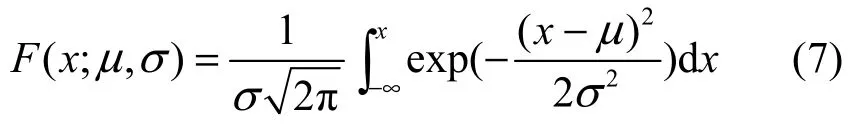
3 OPSO-AEM&NIW算法

种群在进化过程中，每个粒子搜索潜力不尽相同，为充分发挥优势粒子潜力，进一步提高算法效率，本文采取“精英策略(elite strategy)”，给予群体中适应值占优的粒子(称为“精英粒子(elite particle)”)更多的进化机会。若精英粒子在试探过程中探索到新的优势点，则将其替代群体中被选择的劣势个体。然而，过度采取精英策略可能导致易陷入局部最优及最优值振荡等问题。为了克服上述问题，本文引入一种非线性自适应惯性策略来自适应调节各个粒子的活跃程度，增大算法跳出局部最优解的能力，和精英策略相互配合来调节算法全局探索与局部开采之间的平衡，提升反向PSO的性能。

3.1 自适应精英变异策略(AEM)

在精英策略中，精英粒子入选比例的确立对问题的求解起到关键的作用。一方面，比例过大，种群多样性随着进化过程的深入而大幅降低，从而易陷入局部最优；另一方面，一些理论分析表明，在未收敛前，粒子群搜寻的全局最优位总是在先前已知的几个候选解之间来回振荡[13,15]。因此，本文算法仅将种群中gbest位作为精英粒子，在每一代进化过程中，根据式(11)和式(14)对gbest做自适应变异操作，由其产生的新个体对环境做进一步试探。若新个体适应值优于原gbest适应值，则取代之成为新的gbest位参与到新一轮的进化过程中。本文将这种融入精英思想的自适应变异方法称为自适应精英变异策略(AEM,adaptive elite mutation strategy)。

AEM变异操作中，将通过自适应生成变异种子xm及自适应选取变异常量C，产生真实变异量F(xm)代入到式(14)中，实现对精英粒子gbest自适应扰动的目的。具体地，xm的生成综合考虑个体pbest与精英粒子gbest的距离r以及进化代数t的关系，依据式(9)分别计算pbest到gbest在各维上的距离，距离越大，表示群体间相似性越小，再依据适应度标准差st_d的取值不同(见式(13))，自适应取得较大的变异常量C，生成较大变异量F(xm)代入式(14)，使原gbest位自适应获得较大的变异位gbest*。若变异后的f(gbest*)优于f(gbest) (f(·)为问题适应度函数)，gbest将被gbest*取代。新全局最优个体gbest在后续的进化过程中将吸引群体粒子从而帮助粒子跳出局部最优位。由此可见，AEM在算法初期能够自适地使gbest获得足够的扰动，达到扩大搜索空间，增强算法的全局搜索能力的目的；反之，在迭代后期，逐渐减小的变异率使最优解在避免振荡的同时加速了算法的收敛。

在AEM变异中，首先根据式(8)计算变异种子xm在各维上的值。

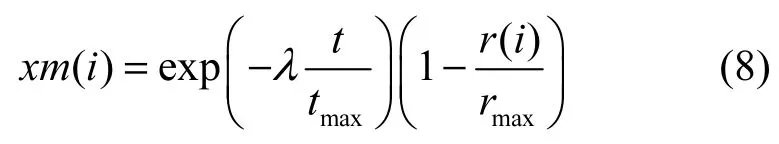
其中，i=1,2,…,D，λ是常数，根据4.2.3节中对参数λ的实验分析结果，在后续算法性能分析实验中取建议值λ=30；t为进化代数，tmax是最大进化代数；r(i)是N个个体的pbest在各维上的平均值avg_pbest(i)到gbest的距离；rmax是各维间最大距离。

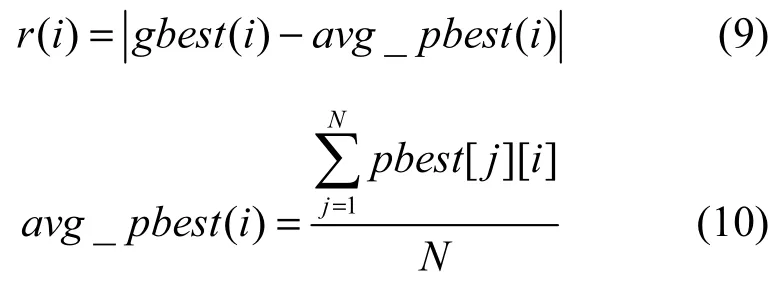
其中，pbest[j][i]是第j个粒子在第i维上的位置。

将xm代入式(11)，自适应产生变异量。

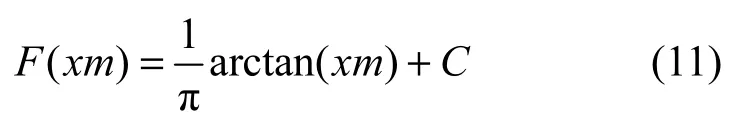
其中，C是一个待定常量，它将根据适应度标准差st_d的不同而自主选取不同的值，具体取值如下

st_d将根据式(13)来判断种群聚集度，其值被分成(0,10−2]、(10−2,10−1]及(10−1,+∞)3段(不同分段点内取值分布情况在本文4.2.3节中做出统计分析)。其中，fi为第i个个体的适应值，fgbest为gbest的适应值。当个体越相似，即fi→fgbest，则st_d取值越小，表示群体越聚集，个体之间的距离越小，C取得的值将越大，对应式(11)产生的变异量越大。图1展示了当C=0.5时变异量F(xm)与xm中变量之间的对应关系。

如图1所示，一方面，当r较小，即群体极值趋于一致时，当前全局最优位将获得较大的变异值(F较大)，算法的搜索能力获得提高；反之，当r逐渐增大，即群体较分散时，变异值的减少(F较小)可避免最优值搜寻过程的回荡，从而加速算法的收敛。另一方面，在迭代初期(t较小)，由于先验认知的不足，种群获得较大的变异值(F较大)，对解空间进行充分的搜索；反之，随着进化的深入(t逐渐增大)，变异值F随之减小，从而确保问题能够平滑地收敛到最优值。

结合上述分析结论，得到自适应精英变异操作如下

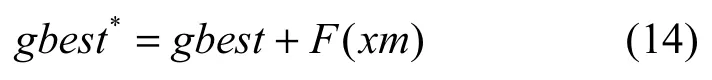
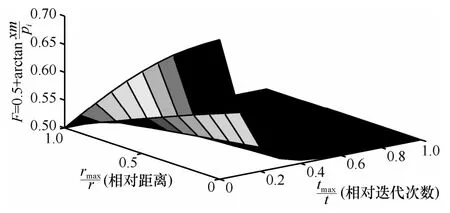
图1 自适应精英变异三维空间

AEM在每一次迭代中，式(14)根据F(xm)对gbest进行扰动，产生变异位gbest*，若f(gbest*)优于f(gbest)，则gbest=gbest*。

3.2 非线性自适应惯性权重更新策略

在速度更新中，本文采用一种如式(15)所示的非线性的自适应策略对粒子惯性权值进行动态调整[16]为

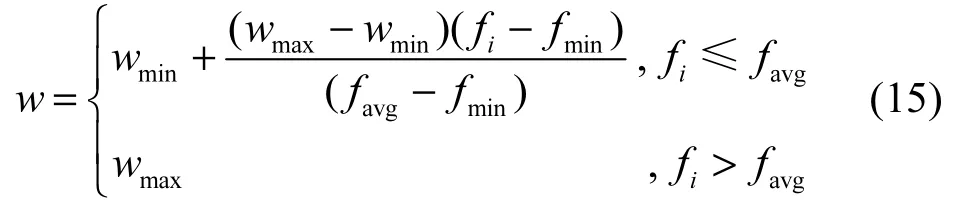
其中，wmin、wmax分别为w的最小值与最大值；fi为粒子i的适应值；fmin、favg分别为当前粒子群的最小适应值和平均适应值。由式(15)可知，当粒子适应值优于平均适应值时，取得最大惯性权重，从而增加粒子的活跃度；反之，取得较小惯性权重，使粒子更多地被精英粒子吸引，从而向优势搜索空间靠拢。同时，当所有粒子趋于一致(此时较小)，w随之增加；较分散时(此时较大)，w随之减小。以上非线性自适应惯性权重更新策略将进一步平衡算法的全局搜索与局部探测能力。

3.3 OPSO-AEM&NIW

本文将AEM与NIW策略同时应用于反向学习PSO算法中，给出了一种带自适应精英扰动及惯性权重的反向粒子群优化算法，算法1用伪代码描述了OPSO-AEM&NIW的基本步骤。其中，OP为当前种群P的反向种群，jr为使用GOBL策略的概率。

3.4 算法时间复杂度分析

对算法1分析可知，OPSO-AEM&NIW算法主要由初始化种群、GOBL策略、速度与位置更新操作、NIW策略以及AEM策略5个部分组成。对于初始化种群和GOBL策略2个部分，除前者包含随机化种群，后者包含边界动态更新外，两者还包含共同部分：反向种群生成及群体选择机制，显然，随机化种群与反向种群的生成，以及边界动态更新部分的时间复杂度均为O(ND)，对于群体选择机制，排序是其主要操作，计算复杂度为O(N2)。特别注意，在低维空间中，通常种群规模N取近似于维度D的数，即N≈D，若维度较高，如D≥100，则通常可取N＜D，计算复杂度O(N2)可计为O(ND)。因此，初始化种群和GOBL策略2个部分的计算复杂度为O(ND)；在OPSO-AEM&NIW中，不难得出，NIW策略、AEM策略以及速度与位置更新操作的计算复杂度均为O(ND)。综上所述，OPSO-AEM&NIW的计算复杂度为O(ND)。

算法1OPSO-AEM&NIW算法

4 数值实验及分析

本文实验将被分成3个部分。1) 算法性能测试，除基本PSO外，OPSO-AEM&NIW还与其他4种基于反向学习的PSO算法(OBL-based PSO)进行比较，分别是OPSO[8]、GOPSO[8]、OVCPSO[10]和EOPSO[9]。实验中，参与对比算法的种群规模N均取40，其他参数保持与原文献一致的设置。2) 策略分析，分析AEM和NIW这2种策略为提高OPSO-AEM&NIW算法性能各自产生的影响，以及两者共同作用下为避免陷入局部最优策略所发挥的作用。3) 参数敏感性分析，观察参数λ(AEM)取不同值时对算法OPSO-AEM&NIW性能的变化情况；并分析AEM策略中待定参数C取不同常量值的平均概率情况；同时，对NIW策略中参数w自适应取值分布进行分析。依据文献[7,17]中对参数c1、c2、jr取值分析，以及本文对参数w、λ的敏感性分析，在后续实验中，若无特别说明，OPSO-AEM&NIW默认参数设置如表1所示。

表1 OPSO-AEM&NIW参数设置

4.1 实验设置

所有实验针对表2所列14个测试函数展开。按其属性分为单峰(f1～f5)和多峰(f6～f14)两大类，其中，多峰函数又被细分为3类：简单多峰函数(f6～f8)、带旋转的多峰函数(f9～f11)和移位多峰函数(f12～f14)。为使所有测试函数在零点位，均取全局最优值0，本文参考CEC 2010[18]中的函数定义，将移位多峰函数中的参数f_bias统一设定为0。具体测试函数如表2所示。

4.2 实验结果与分析

4.2.1 算法对比分析

在6种PSO算法的对比实验中，算法最大迭代次数为10 000，每个测试函数分别运行30次，记录全局最优值的均值。实验采用双尾t检验对各算法结果进行显著性差异统计分析，显著水平为0.05。表3给出了6种对比算法的实验结果，最好结果用黑体显示，下同，表中用“－”、“+”、“～”这3种符号表示OPSO-AEM&NIW算法的性能“劣于”、“优于”、“相当于”对应比较算法。

从表3中可得出OPSO-AEM&NIW在6种算法中都取得了较好的结果。实验结果显示，OPSOAEM&NIW在所有测试函数上均优于OVCPSO；与PSO和OPSO比较，除在f3上处取得相当结果，OPSO-AEM&NIW在其他函数上均取得较优解；EOPSO虽然在f3上取最优解，但在其他12个函数上均劣于OPSO-AEM&NIW。特别地，OPSO-AEM&NIW与GOPSO在大多数函数中取得了相当的最优解，但在4个测试函数f2～f5上，OPSO-AEM&NIW优于GOPSO。

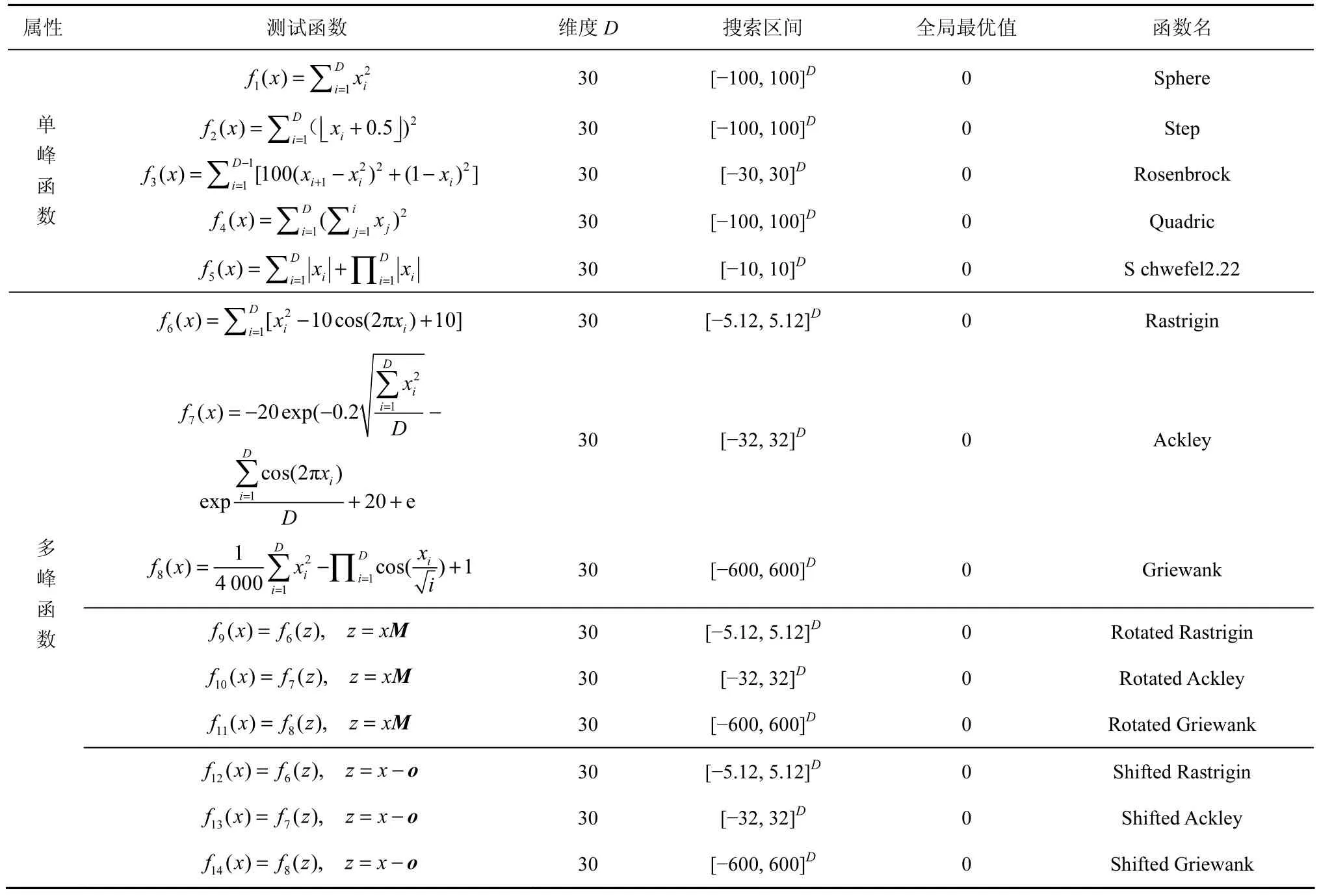
表2 数值实验中使用的14个测试函数

表3 PSO、OPSO、GOPSO、OVCPSO、EOPSO和OPSO−AEM&NIW算法在14个测试函数上的平均适应值

为进一步比较OPSO-AEM&NIW与GOPSO这2种算法性能上的差异，2类实验分别展开。首先除去平均适应值(表3中已记录)，将2种算法运行30次后的另外3个性能指标：标准方差、最佳及最差值分别记录在表4中，结果显示，OPSO-AEM&NIW在12个测试函数中的最差值均优于GOPSO，说明新算法相对GOPSO性能整体较为稳定。另外，2种算法在求解精度为10−16以及最大迭代次数为10 000次的条件下再次进行实验，获得的适应值(fval)及适应值函数评估次数(NFC)如表5所示。通过对NFC值的比较可见，OPSOAEM&NIW (除f10和f13)明显小于GOPSO，实验结果表明OPSO-AEM&NIW大大提升了反向PSO算法的收敛速度。

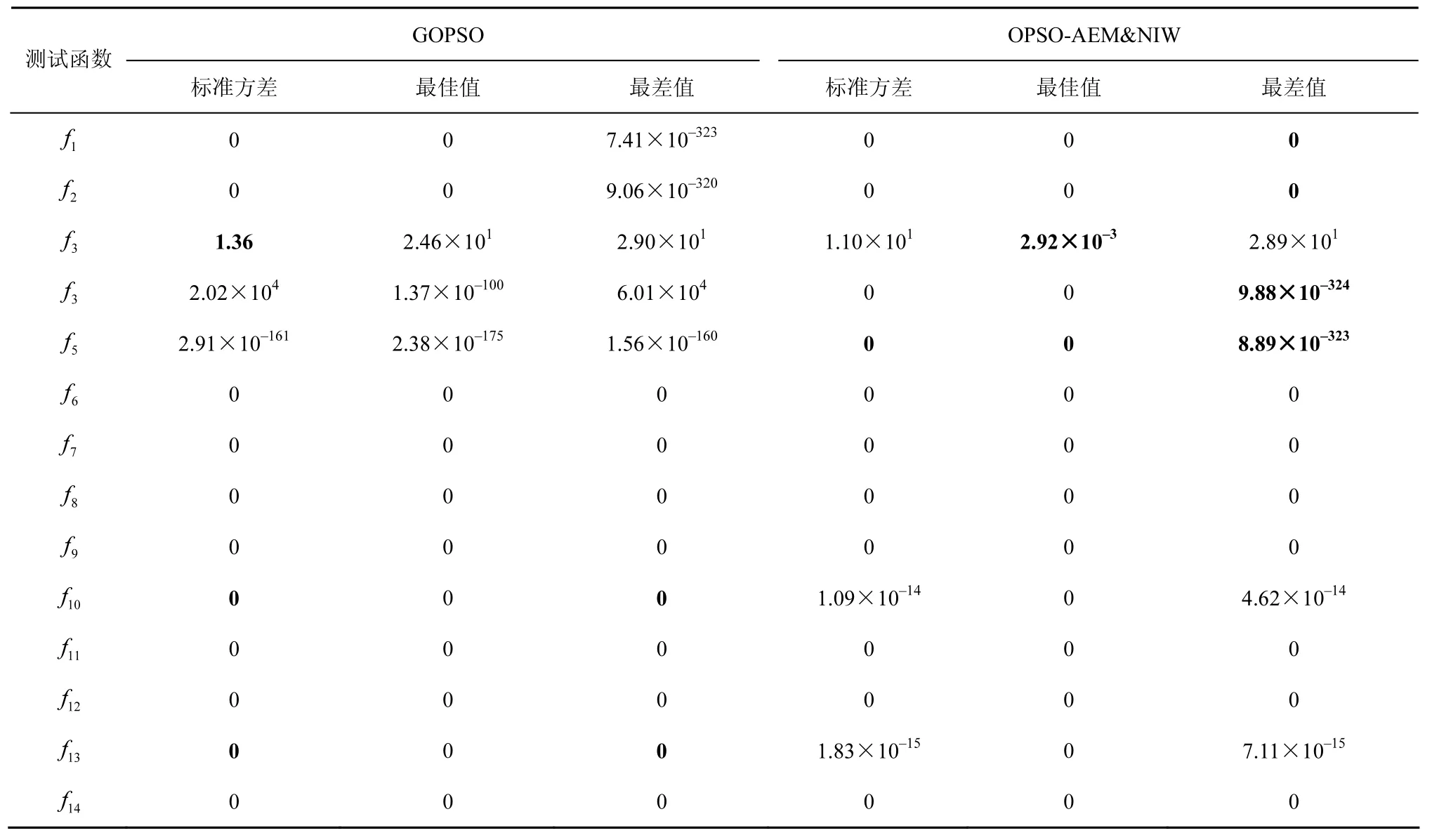
表4 GOPSO和OPSO-AEM&NIW算法在14个测试函数上的运行结果

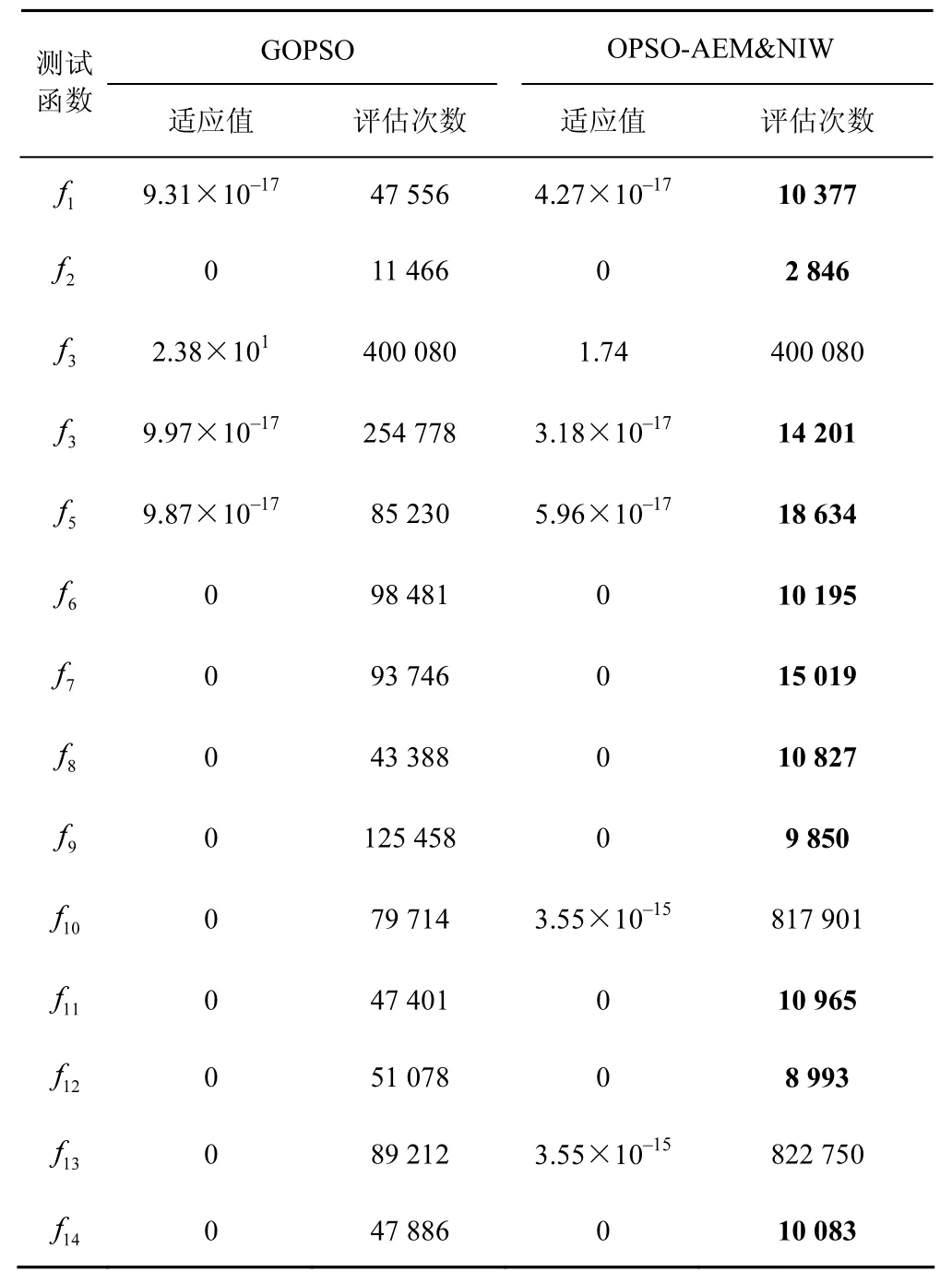
表5 GOPSO和OPSO-AEM&NIW算法在14个测试函数上函数评估次数比较

4.2.2 2种策略有效性分析

为研究自适应精英变异策略与非线性自适应惯性策略在融入到反向学习(GOBL)中后对反向PSO算法性能所产生的影响，以测试函数f2、f9与f14为例，将AEM与NIW这2种策略分别与GOBL结合，形成GOBL+AEM和GOBL+NIW两类算法，与新算法OPSO-AEM&NIW展开性能对比实验。特别指出，在GOBL+ AEM实验中，w取固定值0.729 84[19]。实验结果如图2所示，NIW策略能够充分调动粒子在不同阶段的活跃性，有效平衡算法的全局探索与局部开采能力，加快了算法的收敛速度；AEM策略则通过对精英粒子gbest的扰动，有效避免粒子陷入局部最优的可能性，确保算法得到快速平滑收敛。

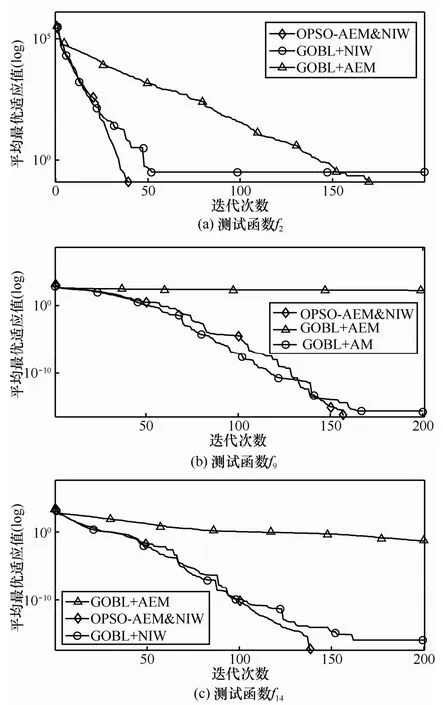
图2 AEM与NIW 2种策略对算法的影响

为从另一侧面了解上述2种策略引入到反向粒子群中为避免算法陷入局部最优所起到的作用，表6分别记录了OPSO算法[7]与OPSO-AEM&NIW算法在30次运行中陷入局部最优的平均次数(MNLO,mean number of local optimum)，以及对应全局最优结果的均值(mean)。实验结果表明，除f4以外，OPSO-AEM&NIW在其他测试函数上的MNLO值均少于OPSO的MNLO值，表明AEM与NIW策略能使粒子在进化过程中有效地避免陷入局部最优的次数，一旦发生，也能采用自适应精英变异策略更成功地跳出局部最优，从而快速地收敛到全局最优值，并表现出较好的稳定性。同时注意到，虽然f4的MNLO在OPSO中更小，但它并没有收敛到全局最优，原因是OPSO算法在处于某个局部最优时无法通过自身的变异操作跳出，进而出现早熟收敛现象。

4.2.3 参数敏感性分析

通过策略分析，对3种策略(GOBL、AEM与NIW)在OPSO-AEM&NIW算法基本PSO性能改进中起到的作用有了清晰的了解。策略中各个参数的设置对算法的性能往往有着很大的影响，文献[7]中已通过实验得出结论：当OBL使用概率jr为0.3时，算法达到最佳性能，本文引用了这一结论。

为检验AEM策略中参数λ的取值对算法性能是否具有一定的影响，通过对14个测试函数上λ在10～60之间取不同的6个整数值时算法OPSOAEM&NIW收敛过程的观测可知，当λ＝30时，所有测试问题都能较平稳而快速地收敛到全局最优解。介于篇幅的限制，图3仅给出了在测试函数f3、f9和f12中OPSO-AEM&NIW参数λ取不同值时算法收敛到全局最优值的进化过程。

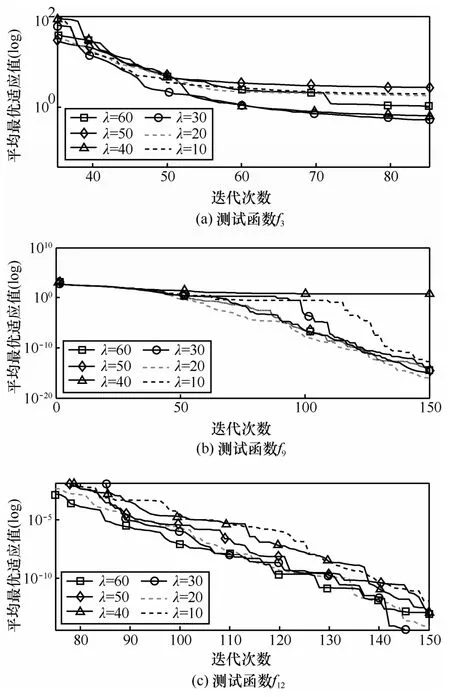
图3 λ在不同取值下OPSO-AEM&NIW全局收敛过程

除此之外，表7统计了AEM策略的另一个待定参数C对14个测试函数在30次实验中自适应取不同常量值时各自的平均概率情况。其中，Mut为变异位占优的次数。特别注意，当C=0.5时，变异式(11)将退化成柯西变异[7]。实验数据表明，相比于柯西变异，自适应精英变异策略将增加25%的概率获得更优的变异位，虽然这看似远小于C=0.5的概率，但其对于算法是否能成功跳出局部最优位是非常关键的。

由4.2.2节分析可知，NIW策略的引入相对于w取固定值时能显著加快算法的收敛速度，而对于其中参数w取值范围(wmax与wmin)，通过反复实验可知，当w取值在0.2～0.5之间时，算法在所有测试函数上取得最好结果。图4以f6为例，展示了算法进化前1 000代过程中w自适应取值的变化情况。由图4可知，随着进化的深入，w取值将趋于0.5，使算法以较大的惯性快速收敛到全局最优值。

表7 AEM变异策略在14个测试函数上取值概率

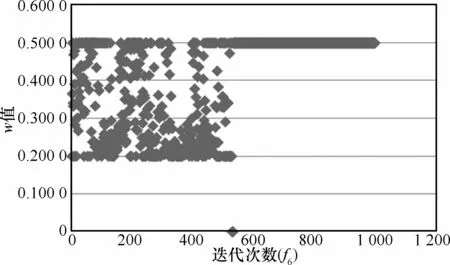
图4 w取值自适应变化情况

5 结束语

本文提出了一种带自适应精英扰动及惯性权重的反向粒子群优化算法。该算法将自适应精英变异和非线性自适应惯性权重2种策略融入到一般性反向学习策略中。为提高全局探索能力，GOBL策略在每代中对解空间与其反向解空间同时进行搜索。AEM策略将全局最优粒子选为精英粒子，根据当前群体聚集程度的不同，自适应选取变异量，使精英粒子获得足够的扰动，并吸引其他粒子向其运动，从而帮助粒子跳出局部最优。NIW策略的引入可进一步克服算法全局探索与局部开采之间的矛盾。它通过自适应获取惯性权值，根据需求调节各个粒子在不同阶段的活跃程度。进化初期，w在一定区间内自适应地变化，以扩大算法的全局搜索空间；随着迭代次数的增加，w取值逐渐趋于平稳，从而有效避免算法最优值的振荡，提高算法的局部开采能力，确保算法平滑快速地收敛到全局最优值。

通过对多种函数的测试结果表明，新算法在获得高精度解的同时，显著提高了算法的收敛速度。在未来的工作中，如何使算法适应更多的问题还需展开更多的实验。另外，算法在高维问题中是否适用及可能存在的问题还需进一步的实验。如何将算法与实际问题相结合是未来研究工作的重点。

[1]KENNEDY J,EBERHART R C.Particle swarm optimization[C]// IEEE International Conference on Neural Networks.Perth,Australia,1995:1942-1948.

[2]史霄波,张引,赵杉,等.基于离散多目标优化粒子群算法的多移动代理协作规划[J].通信学报,2016,37(6):29-37.SHI X B,ZHANG Y,ZHAO S,et al.Discrete multi-objective optimization of particle swarm optimizer algorithm for multi-agents collaborative planning [J].Journal on Communications,2016,37(6):29-37.

[3]INBARANI H H,AZAR A T,JOTHI G.Supervised hybrid feature selection based on PSO and rough sets for medical diagnosis [J].Computer Methods and Programs in Biomedicine,2014,113(1):175-185.

[4]ZAD B B,HASANVAND H,LOBRY J,et al.Optimal reactive power control of DGs for voltage regulation of MV distribution systems using sensitivity analysis method and PSO algorithm [J].International Journal of Electrical Power and Energy System,2015,68:52-60.

[5]SHI Y,EBERHART R C.A modified particle swarm optimizer[C]//The IEEE Congress on Evolutionary Computation (CEC 1998).1998:69-73.

[6]TIZHOOSH H R.Opposition-based learning:a new scheme for machine intelligence[C]//The IEEE International Conference of Intelligent for Modeling,Control and Automation.PiscatNIWay:Inst of Elec.and Elec Eng Computer Society.2005:695-701.

[7]WANG H,LI H,LIU Y,et al.Opposition-based particle swarm algorithm with Cauchy mutation [C]//The IEEE Congress on Evolutionary Computation.2007:356-360.

[8]WANG H,WU Z J,RAHNAMAYAN S,et al.Enhancing particle swarm optimization using generalized opposition-based learning [J].Information Sciences,2011,181:4699-4714.

[9]周新宇,吴志健,王晖,等.一种精英反向学习的粒子群优化算法[J].电子学报,2013,41(8):1647-1652.ZHOU X Y,WU Z J,WANG H,et al.Elite opposition-based particle swarm optimization[J].Acta Electronica Sinica,2013,41(8):1647-1652.

[10]SHAHZAD F,BAIG A R,MASOOD S,et al.Opposition-based particle swarm optimization with velocity clamping (OVCPSO) [J].Advances in Computational Intell,2009:339-348.

[11]KAUCIC M.A multi-start opposition-based particle swarm optimization algorithm with adaptive velocity for bound constrained global optimization[J].J Glob Optim,2013,55:165-188

[12]PEHLIVANOGLU Y V.A new particle swarm optimization method enhanced with a periodic mutation strategy and neural networks [J].IEEE Trans Evol Comput.2013,17:436-452.

[13]KARAFOTIAS G,HOOGENDOORN M,EIBEN A E.Parameter control in evolutionary algorithms:trends and challenges[J].IEEE Transactions on Evolutionary Computation,2015,19:167-187.

[14]汪慎文,丁立新,谢承旺,等.应用精英反向学习策略的混合差分演化算法[M].武汉大学学报(理学版),2013,59(2):111-116.WANG S W,DING L X,XIE C W,et al.A hybrid differential evolution with elite opposition-based learning [J].Journal of Wuhan University,2013,59(2):111-116.

[15]OZCAN E,MOHAN C K.particle swarm optimization:surfing and waves[C]//Congress on Evolutionary Computation (CEC1999).1999:1939-1944.

[16]龚纯,王正林.精通MATLAB最优化计算[M].电子工业出版社,2012:283-285.GONG C,WANG Z L.Proficient optimization calculation in MATLAB [M].Electronic Industry Press,2012:283-285.

[17]FRANS V D B.An analysis of particle swarm optimizers[D].Department of Computer Science,University of Pretoria,South Africa,2002.

[18]TANG K,LI X D,SUGANTHAN P N,et al.Benchmark functions for the CEC’2010 special session and competition on large-scale global optimization[R].Nature Inspired Computation and Applications Laboratory,USTC,China,20092,1.

[19]BERGH F,ENGELBRECHT A P.Effect of swarm size on cooperative particle swarm optimizers[C]//Genetic and Evolutionary Computation Conference.2001:892-899.

董文永（1973-），男，河南南阳人，博士，武汉大学教授、博士生导师，主要研究方向为演化计算、智能仿真优化、系统控制、机器学习等。

康岚兰（1979-），女，江西赣州人，武汉大学博士生，江西理工大学讲师，主要研究方向为演化计算、机器学习等。

刘宇航（1979-），男，湖北孝感人，武汉大学博士生，主要研究方向为统计机器学习及相关应用。

李康顺（1962-），男，江西兴国人，博士，华南农业大学教授、博士生导师，主要研究方向为智能计算、多目标优化、视频流图像识别等。

Opposition-based particle swarm optimization with adaptive elite mutation and nonlinear inertia weight

An opposition-based particle swarm optimization with adaptive elite mutation and nonlinear inertia weight (OPSO-AEM&NIW) was proposed to overcome the drawbacks,such as falling into local optimization,slow convergence speed of opposition-based particle swarm optimization.Two strategies were introduced to balance the contradiction between exploration and exploitation during its iterations process.The first one was nonlinear adaptive inertia weight (NIW),which aim to accelerate the process of convergence of the algorithm by adjusting the active degree of each particle using relative information such as particle fitness proportion.The second one was adaptive elite mutation strategy (AEM),which aim to avoid algorithm trap into local optimum by trigging particle’s activity.Experimental results show OPSO-AEM&NIW algorithm has stronger competitive ability compared with opposition-based particle swarm optimizations and its varieties in both calculation accuracy and computation cost.

generalized opposition-based learning,particle swarm optimization,adaptive elite mutation,nonlinear inertia weight

The National Natural Science Foundation of China (No.61170305，No.61672024)

TP181

A

10.11959/j.issn.1000-436x.2016224

DONG Wen-yong1,KANG Lan-lan1,2,LIU Yu-hang1,LI Kang-shun3

(1.Computer School,Wuhan University,Wuhan 430072,China;2.Faculty of Applied Science,Jiangxi University of Science and Technology,Ganzhou 341000,China;3.College of Information,South China Agricultural University,Guangzhou 510642,China)

2015-09-22；

2016-09-09

康岚兰，victorykll@163.com

资助项目（No.61170305，No.61672024）