基于最大相关熵的通信辐射源个体识别方法

唐哲，雷迎科

（电子工程学院，安徽 合肥 230037）

基于最大相关熵的通信辐射源个体识别方法

唐哲，雷迎科

（电子工程学院，安徽 合肥 230037）

采用相关熵度量辐射源细微特征之间的相似性，提出一种基于最大相关熵的通信辐射源个体识别方法。首先提取矩形积分双谱特征来表征辐射源个体差异，并基于最大相关熵准则构造优化函数；其次利用半二次优化技术，将非线性的优化问题转化为加权线性最小二乘问题；最后利用有效集算法得到稀疏系数构造分类器，实现通信辐射源的个体识别。在实际采集的同厂家同型号的FM电台数据集上，验证了方法的可行性与有效性。

通信辐射源个体识别；最大相关熵；稀疏表示；半二次优化；线性互补问题；有效集算法

1 引言

早期的通信辐射源个体识别问题，主要结合“turn-on”暂态信号特征[2,3]和小波分析、分形等理论，针对不同型号的电台信号进行研究。但由于实际应用中暂态信号特征存在难以提取和难以用于识别同厂家同工作模式的辐射源个体等问题[4]，近年来，大部分研究主要利用稳态信号特征[5～7]对辐射源进行个体识别。由于双谱能够很好地抑制高斯噪声，被广泛用于表征信号的稳态特征，在双谱的基础上，矩形积分双谱（SIB,square integral bispectra）具有时移不变性、尺度变化性以及部分相位保持性等特点，并且不会漏掉或重复双谱信息。Xu等[8]在提取SIB特征的基础上，利用主成分分析（PCA,principal component analysis）进行特征降维，在实际采集的数据集上的识别率高达90%以上，但该方法的识别性能容易受PCA约简维数的影响，算法稳定性较差。针对高阶谱特征的高维特性，结合机器学习等相关理论来实现辐射源的个体识别逐渐成为新的研究热点[9,10]。在实际应用中，辐射源发射机产生的信号都是非平稳和非高斯的，导致其细微特征通常是不稳定、非高斯和非线性的，此时高阶谱特征并不能够很好地表征辐射源个体特征。信息论中的相关熵（correntropy）在处理非高斯噪声[11]、冲激噪声[12]以及度量局部相似度[13]方面具有良好的性能，从而能够深刻地表征信号的细微差异。He[14]将相关熵与稀疏表示（SR,sparse representation）[15]相结合，提出了基于相关熵的稀疏表示（CESR,correntropy-based sparse representation）算法，在人脸数据集上取得了顽健而高效的分类效果。

针对同型号同厂家同工作模式下的通信辐射源个体识别问题，本文提出基于最大相关熵的通信辐射源个体识别方法（MCER）。首先，在特征提取阶段利用SIB特征去除高斯噪声影响，来表征辐射源的个体差异，而在稀疏表示阶段利用最大相关熵模型去除非高斯噪声影响，增强算法的顽健性；其次，利用l2范数约束系数，挖掘样本之间的相关性来缓解“小样本”问题，并通过有效集算法得到稀疏系数；最后，进一步利用系数中的判别性信息，构造分类器。在实际采集的FM电台数据集下，验证了算法的有效性和实际应用价值。

2 基于最大相关熵的识别方法

2.1 最大相关熵表示算法

综合孵化器是专业孵化器的基础，专业孵化器是综合孵化器的升华。科学统筹综合孵化器和专业孵化器的发展，才能既推动孵化企业的繁荣，又助推孵化集群的显现。统筹综合孵化器与专业孵化器的发展，就是要针对两种孵化器特点，开展专业的协调和服务。

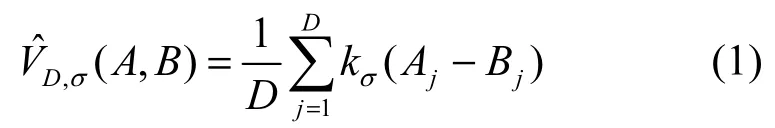
其中，kσ为高斯核函数。当两随机变量的相关性越强时，相关熵越大；反之，相关熵越小。假定在RD中训练集X=[x1,x2,…,xn]∈RD×n包含n个训练样本，y∈RD表示测试样本。则第i类训练子集包含ni个训练样本，，训练集由m类训练样本组成，即X=[X1,X2,…,Xi,…,Xm]由m个训练子集构成。通过最大化相关熵，可以得到对测试样本的表示系数，使训练样本的线性表示与测试样本的差异最小

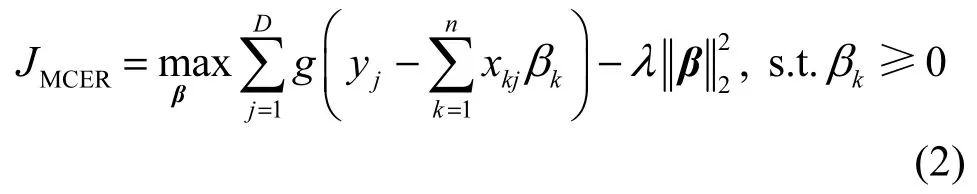
根据凸共轭函数[16]的性质，式(2)可转化为

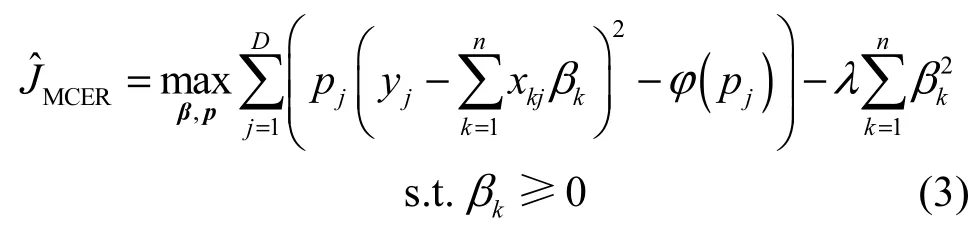
其中，p=[p1,p2,…,pD]T是由于半二次优化而引入的辅助变量，β为系统向量，当β固定时，，某一局部最大值(β,p)可以通过迭代计算

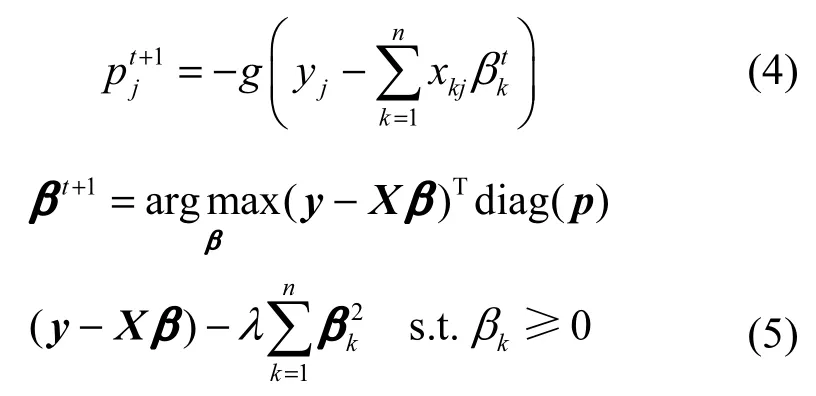
其中，t表示第t次迭代，diag(·)表示将向量p转换为一个对角阵。式(5)显示，在计算之后，辅助变量p在优化βt+1时退化为一权重系数。基于Karush-Kuhn Tucker （KKT）优化条件[17]，式(5)可以转化成以下单调线性互补问题。

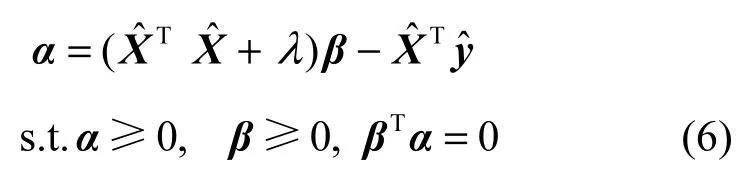
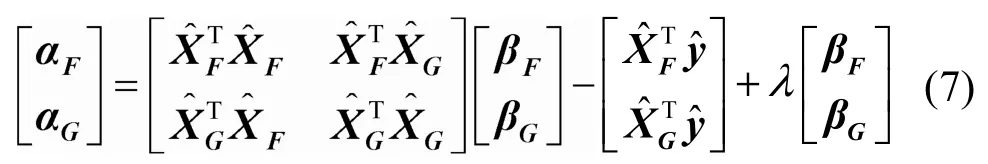
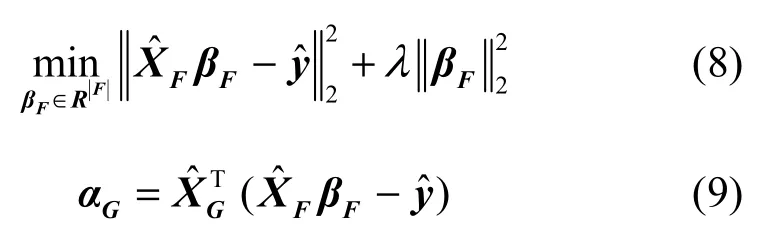
最终，最大相关熵表示算法（MCER）得到的优化结果可以写成。MCER中的核宽度可以表示为

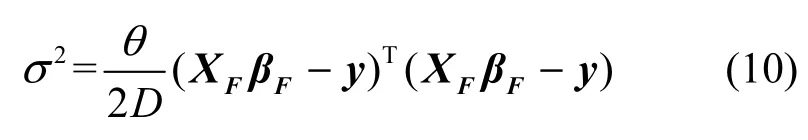
其中，θ为控制噪声的常数，D为训练样本量长度。为简化优化问题，本文令θ恒为1进行相关计算。

最大相关熵表示算法如下所示：步骤1到步骤4计算了在确定的tp下，目标函数的一个可行解β。在步骤5计算了第t+1次迭代中的辅助变量t+1p。该算法不断最大化目标函数式(3)直至其收敛，得到最终的系数β。

MCER算法如下。

输入训练集X，测试样本y，p1=−1，F=φ，，β=0，α=−XTy。

输出系数β。

步骤1计算。

步骤2计算最小项下标。如果，令；否则，停止算法：β∗=β即为最优解。

步骤3通过式(8)计算。如果，令转至步骤4；否则令r为

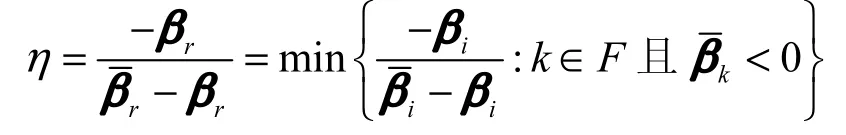
步骤3根据式(6)计算α。

步骤4分别根据式(4)和式(10)更新辅助向量t+1p和核尺寸σ。并返回步骤1。

在没有稀疏约束的条件下，MCER中的有效集算法保证了系数β的稀疏性，从而在l2范数的约束下同样得到了对测试样本的稀疏表示。

2.2 最大相关熵表示算法的分类器设计

在分类阶段，为了防止产生较大的系数，造成错误的分类结果，需要进一步利用系数β中包含的判别性信息，构造残差

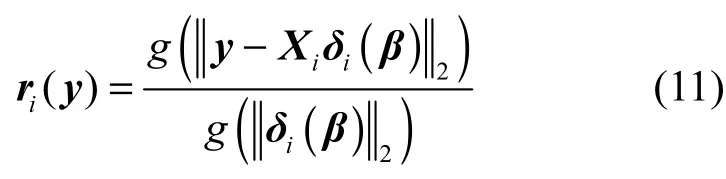
其中，δi(β)表示属于类别i的系数，g(·)中的2个核宽度计算如下

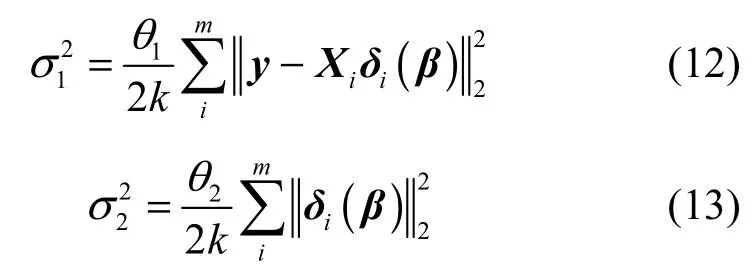
其中，k为测试样本长度，同样，本文将θ1和θ2设为1进行相关计算。最后，利用得到的每类样本的残差，实现对测试样本y的分类

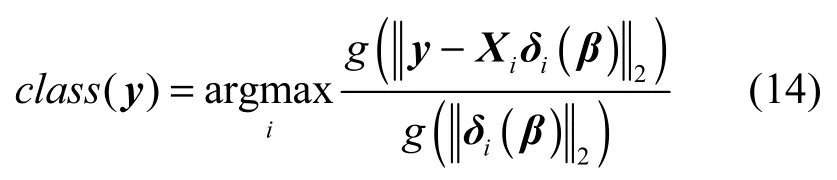
3 实验结果分析

实验数据为在相同工作模式下实际采集的10部同厂家同型号FM电台的零中频I/Q正交信号。信号的中心频率160 MHz，信号带宽为25 kHz，接收机的信道带宽为100 kHz。将信号降至零中频后，以204.8 kHz的采样频率对信号进行采样，采样2.5 s后，得到由511 829个样本点构成的样本序列，每个电台采集18个样本序列。

对于实际采集的FM复信号，瞬时相位包含了FM信号丰富的频率信息，反映了数据的实部和虚部之间的非线性比例关系以及频率合成器在调制信号时的工作特性。因此，本文选择FM复信号的瞬时相位来提取SIB特征作为辐射源的细微特征，用于表征通信辐射源的个体差异。SIB特征提取时，分别利用每部电台的18个样本序列进行SIB计算，共得到180个256维的SIB特征向量，构成总的SIB特征集，即为180×256的矩阵，如图1所示。

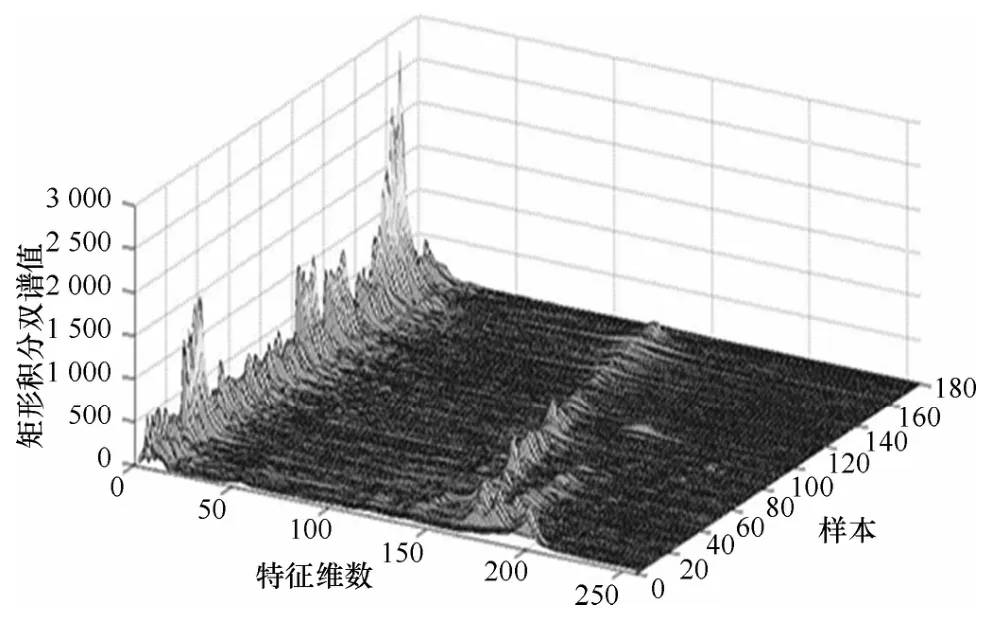
图1 180个原始信号SIB特征集

本文采用最大相关熵分类器（MCERC）对电台进行个体识别，而近邻数为1的最近邻分类器（NNC）、基于高斯核的支持向量机分类器（SVM）以及基于相关熵的稀疏表示分类器（CESRC）作为参考同样对提取的SIB特征进行分类。实验结果均为20次实验得到的平均值。

3.1 对10部FM电台的识别

为了衡量训练样本个数对分类结果的影响，将每部电台18个样本序列的SIB特征向量按比例随机划分为训练样本和测试样本，构成训练集和测试集，实验结果如表1所示。当训练样本较少（20～40）时，MCERC识别率在70%以下；当训练样本充足时，MCERC的识别率能够达到80%以上。

表1 10部FM电台的平均识别率

表1中的数据显示，在不同的实验中，随着训练样本的增多，SVM的识别效果最差，MCERC均取得最好的识别效果，比NNC的识别率高出10%左右。以训练样本个数为60（测试样本个数为120）为例，MCERC通过l2范数松弛对系数的稀疏约束，一定程度上缓解了识别过程中的“小样本”问题，从而得到更为优异的识别效果，比NNC高10%左右，比SVM高20%左右，而比CESRC高20%左右。

图2显示，在训练样本个数分别为20、80以及140时，MCERC和CESRC对不同电台的平均识别效果。电台1～3的识别难度最小，SIB特征能够很好地表征其个体差异；而电台6～8的识别难度较大，彼此的SIB特征较为相似并互相影响识别，使各自的分类识别效果较差。在对不同电台的识别中，采用l2范数松弛对系数的稀疏约束，通过有效集算法保证系数稀疏性，并利用系数内包含的判别性信息，MCERC的识别结果更为稳定优异。

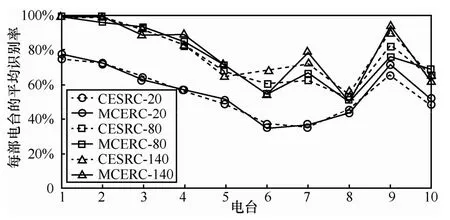
图2 对不同电台的平均识别率

3.2 算法的稀疏表示特性

通过计算系数β的稀疏度S，可以衡量算法对测试样本稀疏表示的能力，体现算法的稀疏表示特性，其计算式为

从图3中可以看到，当训练样本增多时，由于l2范数的稀疏约束弱于l1范数，CESR能够得到比MCER更为稀疏的系数。在不同训练样本个数的条件下， MCER算法与CESR算法所得的系数稀疏度相差约为5%，说明在没有稀疏约束的情况下，SIB特征的高维性和有效集算法弥补了l2范数的稀疏约束能力，保证MCER算法的稀疏表示特性。

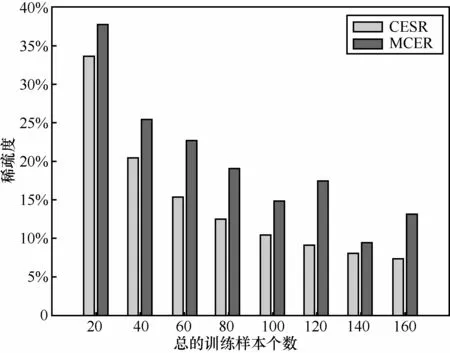
图3 ε=0.001时CESR和MCER算法的稀疏度

4 结束语

本文提出一种基于相关熵的通信辐射源个体识别方法，该方法提取FM信号瞬时相位的SIB特征来表征辐射源个体差异，在最大相关熵模型的基础上引入l2正则项来缓解“小样本”问题，通过有效集算法保证了系数的稀疏性，并利用系数内包含的判别性信息构造分类器，实现辐射源的个体识别。在实际的FM复信号数据集上取得了较好的识别效果，对实际应用当中的辐射源个体识别具有较强理论与应用价值。

[1]DIETRICH J.A wavelet analysis of transients in phase-locked loops[D].Winnipeg,Canada,University of Manitoba,1994.

[2]TEKBAS Ö H,ÜRETEN O,SERINKEN N.Improvement of transmitter identification system for low SNR transients[J].Electronics Letters,2004,40(3):182-183.

[3]SERINKEN N,ÜRETEN O.Generalised dimension characterisation of radio transmitter turn-on transients[J].Electronics Letters,2000,36(12):1064-1066.

[4]GERDES R,DANIELS T,MINA M,et al.Device identification via analog signal fingerprinting:a matched filter approach[C]//13th Annual Network and Distributed System Security Symposium.2006.

[5]蔡忠伟,李建东.基于双谱的通信辐射源个体识别[J].通信学报,2007,28(2):75-79.CAI Z W,LI J D.Study of transmitter individual identification based on bispectra[J].Journal on Communications,2007,28(2):75-79.

[6]张旻,钟子发,王若冰.通信电台个体识别技术研究[J].电子学报,2009,37(10):2125-2129.ZHANG M,ZHONG Z F,WANG R B.Research on the technique of individual communication transmitter identification[J].Acta Electronica Sinica,2009,37(10):2125-2129.

[7]顾晨辉,王伦文.基于瞬时包络特征的跳频电台个体识别方法[J].信号处理,2012,28(9):1335-1340.GU C H,WANG L W,Individual frequency hopping radio identification method based on instantaneous envelope characteristics[J].Signal Processing,2012,28(9):1335-1340.

[8]XU S H,HUANG B X,XU Z G.Identification of individual radio transmitters based on selected surrounding-line integral bispectra[C]//The 9th International Conference on Advanced Communication Technology.Gangwon-Do,South Korea,2007:1147-1150.

[9]WANG X B,WU Y Y,CARON B.Transmitter identification using embedded spread spectrum sequences[C]//2003 International Conference on Communication Technology.Beijing,China,2003:1517-1523.

[10]WANG X B,WU Y Y,CARON B.Transmitter identification using embedded pseudo random sequences[J].IEEE Transactions on Broadcasting,2004,50(3):244-252.

[11]LIU W,POKHAREL P P,PRINCIPE J C.Correntropy:properties and applications in non-Gaussian signal processing[J].IEEE Transactions on Signal Processing,2007,55(11):5286-5298.

[12]POKHAREL P P,LIU W F,PRINCIPLE J C.A low complexity robust detector in impulsive noise[J].Signal Processing,2009,89(10):1902-1909.

[13]LIU W F,POKHAREL P P,PRINCIPLE J C.Correntropy:a localized similarity measure[C]//2006 International Joint Conference on Neural Networks.Vancouver,Canada,2006:4919-4924.

[14]HE R,ZHENG W S,HU B G.Maximum correntropy criterion for robust face recognition[C]//IEEE Transactions on Pattern Analysis and Machine Intelligence,2011,33(8):1561-1576.

[15]WRIGHT J,YANG A Y,GANESH A,et al.Robust face recognition via sparse representation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2009,31(2):210-217.

[16]BOYD S,VANDENBERGHE L.Convex optimization[M].New York:Cambridge University Press,2004.

[17]WRIGHT S J.On reduced convex QP formulations of monotone LCPs[J].Mathematical Programming,2001,90(3):459-473.

[18]LEE H,BATTLE A,RAINA R,et al.Efficient sparse coding algorithms[C]//The Twentieth Annual Conference on Neural Information Processing Systems.Vancouver,Canada,2006:4-7.

唐哲（1991-），男，山东临沂人，电子工程学院硕士生，主要研究方向为通信信号处理。

雷迎科（1975-），男，安徽安庆人，博士，电子工程学院副教授，主要研究方向为通信信号处理。

Method of individual communication transmitter identification based on maximum correntropy

TANG Zhe,LEI Ying-ke
(Electronic Engineering Institute,Hefei 230037,China)

To measure the similarity between the fine features of communication transmitters,a method of individual communication transmitter identification based on maximum correntropy was put forward.Firstly,the square integral bispectra was extracted to characterise the communication transmitters,and then optimization function based on maximum correntropy criterion was constructed.Secondly,the half-quadratic technique transformed the nonlinear optimization problem to a weighted linear least squares problem.Finally,for identifying the communication transmitters,the sparse coefficient computed by active set algorithm was utilized to construct the classifier.Using the FM radios with same manufacturer and model,the actually collected data sets verified the feasibility and effectiveness of the method.

individual communication transmitter identification,maximum correntropy,sparse representation,half-quadratic,linear complementary problem,active set algorithm

s:National Defense Science and Technology Key Laboratory Fund Project (No.9140C130502140C13068),Preliminary Assembling Project Fund (No.9140A33030114JB39470),The National Natural Science Foundation of China (No.61272333)

TN911.7

A

10.11959/j.issn.1000-436x.2016283

2015-11-03；

2016-08-23

雷迎科，leiyingke@163.com

国防科技重点实验室基金资助项目（No.9140C130502140C13068）；总装预研基金资助项目（No.9140A33030114JB39470）；国家自然科学基金资助项目（No.61272333）