拉伸式3-D多涡卷混沌系统的设计及其在保密通信中的应用
马均澎,王丽丹,段书凯,吴洁宁
(西南大学电子信息工程学院非线性电路与智能信息处理重庆市重点实验室,重庆 400715)
拉伸式3-D多涡卷混沌系统的设计及其在保密通信中的应用
马均澎,王丽丹,段书凯,吴洁宁
(西南大学电子信息工程学院非线性电路与智能信息处理重庆市重点实验室,重庆 400715)
基于典型的Chua式电路,提出了一种拉伸式多涡卷混沌系统。首先,通过系统的对称性、不变性、耗散性、系统平衡点和稳定性,分析了混沌的分维特性、时域波形、Lyapunov指数谱等基本的混沌动力学特性。其次,利用PSPICE实现了该系统的混沌电路。最后,结合Lyapunov稳定性原理,运用单向耦合法,探究了该混沌系统的同步性问题,并采用该方法有效地实现了特定信号的加密、解密。数值仿真与实验结果保持一致,进一步证实了该方法的可行性。
Chua电路;保密通信;多涡卷混沌吸引子;电路实现
1 引言
自20世纪70年代中期,Lorenz[1]揭开混沌学研究的历史序幕至今,混沌科学得到十分迅猛的发展,目前已在电路、信息处理、人工神经网络等众多领域[2~4]得到了极为广泛的关注。1990年,Pecora等[5]首次研究了Newcomb电路的混沌同步,将其引入保密通信,打破了混沌研究与保密通信中存在的技术壁垒。自此,混沌保密通信技术的研究进入高速通道,成为世界各国的重要研究课题,并在该领域取得了巨大成就[6~8]。相较于传统密码学出现的自同步密码系统的传输错误以及有限的密钥空间,混沌同步保密通信由于其特殊的加密方式,不仅有效地避免了该错误扩散的产生[9],而且系统对应的密钥为一定范围内的实数集,其中的每一个值都可能被取到,进而提升了保密系统的密钥空间和破译难度等[9]。这些优势极大地促进了混沌理论和混沌加密在信息安全领域的研究,其中,如何构造复杂多变的混沌系统已成为国内外专家、学者研究的热点问题。
近年来,随着混沌控制理论趋于成熟,研究人员先后提出了Chen系统[10]、Jerk系统[11]、Lv系统[12]等。其中,Chua式多涡卷混沌系统一直是众多理论和实验研究的重点[13]。由于此类混沌系统可以展示出丰富的动力学特性以及多变的混沌结构[14,15],因而在保密通信和信息隐藏等方面具有极为广阔的应用前景[9]。目前,对于Chua式多涡卷混沌系统的研究,主要是利用间断函数[16]、sigmoid函数[17]、多重分段线性函数[18]等替代Chua式二极管,构建出了诸如变形Chua氏电路[19]、Chua氏对偶混沌电路[20]、多涡卷Chua氏电路[21]等多种涡卷混沌系统。但这类实验结果大多呈现出混沌涡卷的自我重复[22~25],而其他类型涡卷结构的提出,却鲜有报道。
针对以上问题,本文在Chua电路[13]的基础上,提出了一种拉伸式多涡卷混沌系统。该系统通过Heaviside函数将之前的涡卷结构拉伸为“半涡卷”状态,使其混沌轨迹由平面变为立体,从而成功地摆脱了多涡卷混沌吸引子在多方向上单一的涡卷复制结构。另外,改变系统的部分参数密钥还可以控制其混沌轨迹,使其出现更为复杂、多变的混沌结构。通过理论推导、数值仿真、Lyapunov指数谱等研究了该系统的基本动力学特性,同时,针对该系统设计了PSPICE电路。最后,利用线性反馈控制法探究了混沌系统的同步问题,并采用单向耦合法实现了特定的物理信号与混沌系统的加密、解密。由于该混沌系统展现出丰富的动力学特性,因而在保密通信中[26,27]具有更为优越的保密性能和保密效果[9]。
2 构造新型3-D多涡卷混沌吸引子
2.1 构造单方向多涡卷混沌吸引子
基于相关文献[28,29]的研究成果,在Chua式电路的基础上,利用多项式平移的方法在x方向上构造出多涡卷混沌吸引子,其无量纲状态方程如下
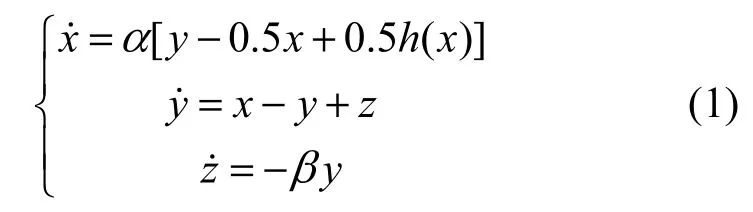
其中,x、y、z为状态变量,α和β为系统参数。h(x)的分段线性函数表示为
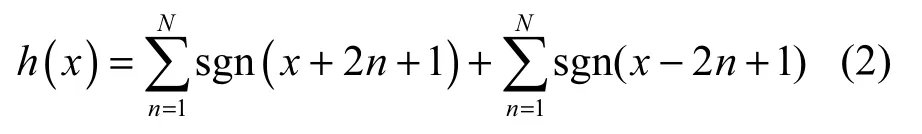
当x<0时,sgn (x) = −1;当x>0时,sgn (x)=1。该系统在x轴方向可产生2N+1个涡卷混沌吸引子。令N= 3,α= 10,β=16,根据式(1)和式(2),得到7涡卷混沌吸引子的数字仿真结果,如图1所示。
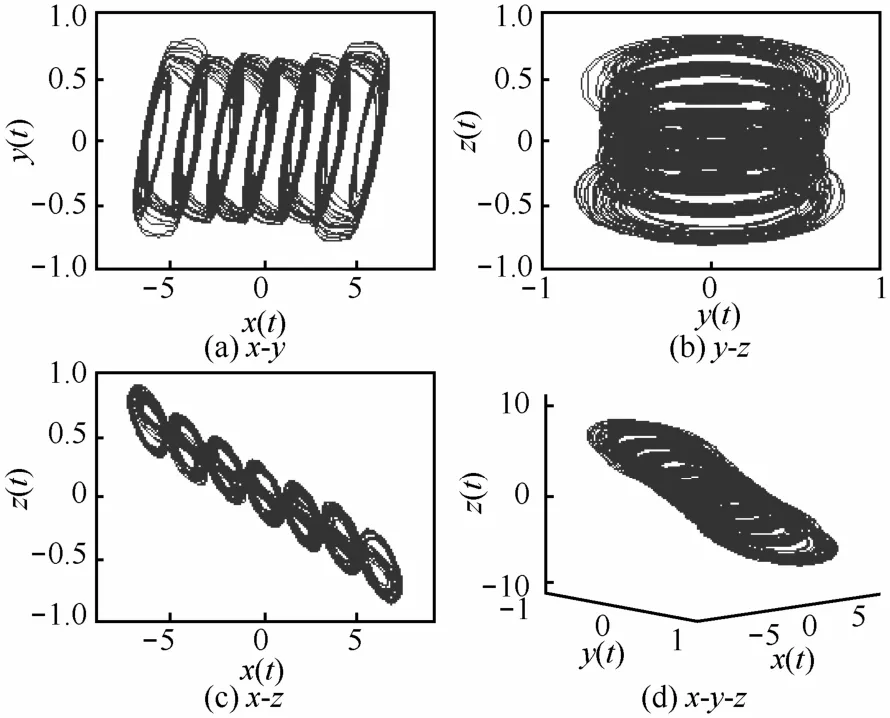
图1 系统(1)的混沌吸引子
2.2 构造拉伸式3-D多涡卷混沌吸引子
通过进一步研究,本文将同类型的分段函数f(x)和d(z)引入系统(1)中,可以使该混沌吸引子沿z方向进行拉伸扩展,从而构造出了拉伸式3-D多涡卷混沌吸引子,其无量纲方程式如下
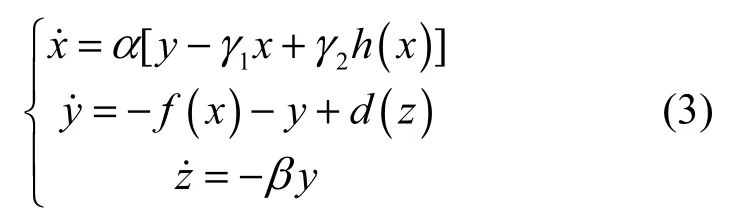
其中,h(x)如式(2)所示,f(x)、d(z)的分段线性函数表示如下
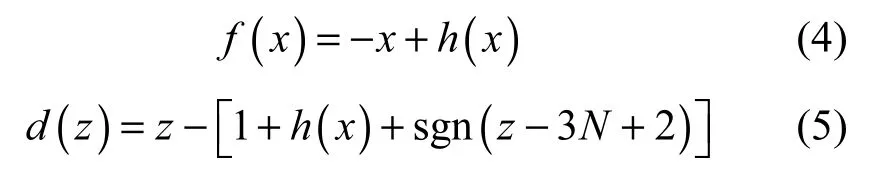
这里选取α= 10,β= 16,N =3,初值为 (2,0.5,0.005)。采用三阶Runge-Kutta算法,得到多涡卷混沌吸引子相图,如图2所示。通过对比系统(1)和系统(3)的结构不难发现:系统(1)只是单纯的涡卷横向扩展,而系统(3)则是在系统(1)的基础上对其进行了拉伸扩展,使该涡卷混沌系统变为“半涡卷混沌”系统,特别是在图1和图2(a)中的混沌结构发生了明显变化,可以观察到系统沿z方向上通过拉伸,使本该重叠在某一平面上的涡卷结构,产生了分离。这是之前很多混沌结构没有出现过的一种现象。同时,观察图2(b)~图2(d),γ1= 0.45固定不变,随着γ2的增大,特别是在y−z平面上,系统逐渐出现复杂的涡卷混沌特性。
3 基本动力学分析
3.1 对称性和不变性
由于在变换(x,y,z)→(−x, −y, −z)下,系统(3)的相图均保持不变,即系统的吸引子关于原点对称,并且这种自然的对称性对所有的系统参数都保持不变。
3.2 耗散性和吸引子的存在性
根据
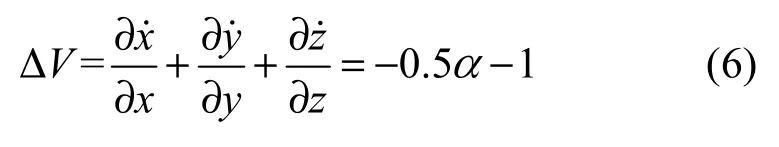
当0.5α+1 > 1时,则系统(3)是耗散的,以指数形式收敛。
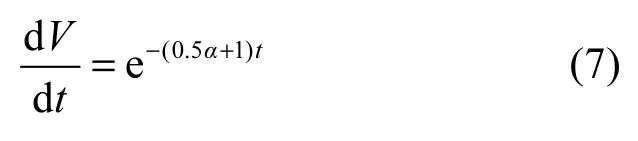
即体积元V0在t时刻收缩为体积元V0e−(0.5α+1)t。这意味着当t→∞时,包含系统轨迹的每个体积元以指数率−(0.5α+1)收缩到0。所有系统轨迹线最终会被限制在一个体积为0的集合上,并且其渐进运动固定在一个吸引子上。
3.3 平衡点及稳定性
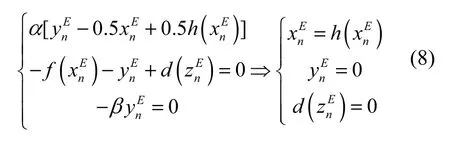
以N= 3的情况为例,通过对式(8)进行求解,可得系统(3)的平衡点分布如图3所示,图中“o”表示指标2的鞍焦平衡点。
通过对系统(3)进行线性化,可以得到其平衡点对应的雅可比矩阵为
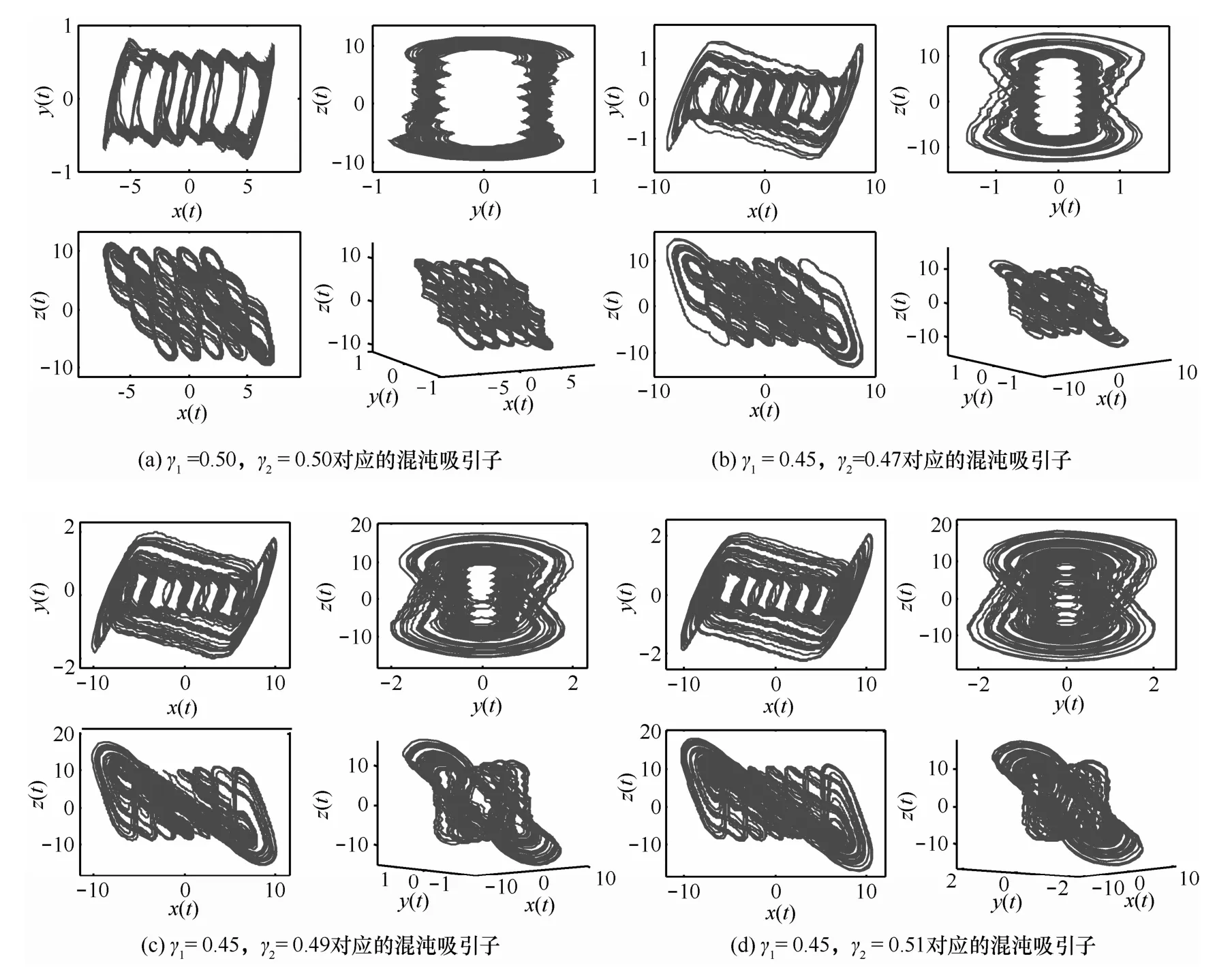
图2 γ1、γ2取不同值时,系统(3)产生的多涡卷混沌吸引子
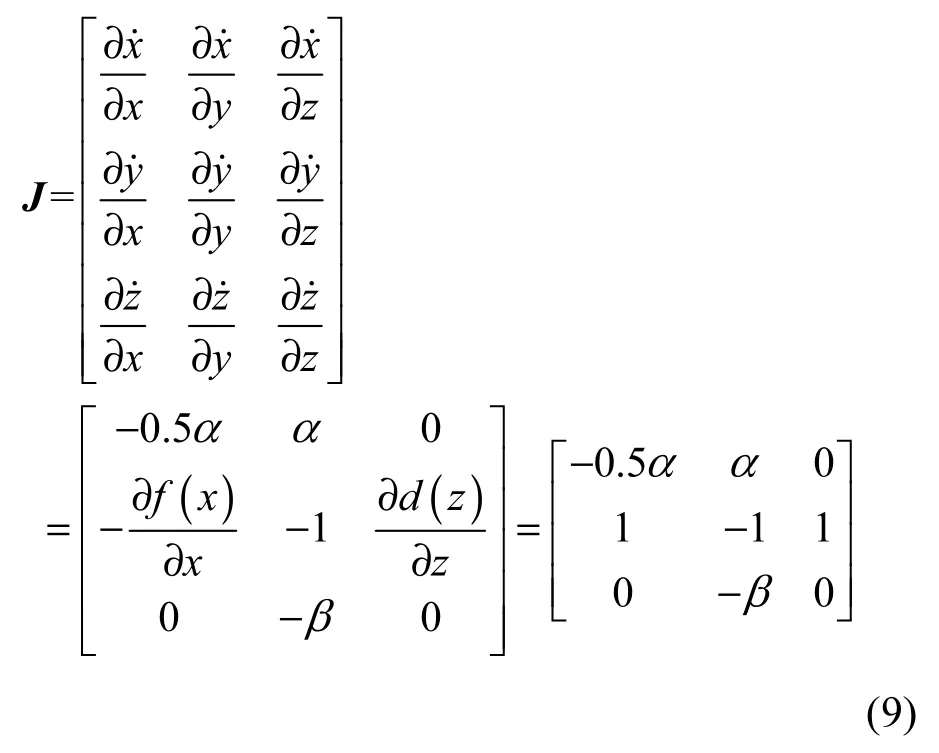
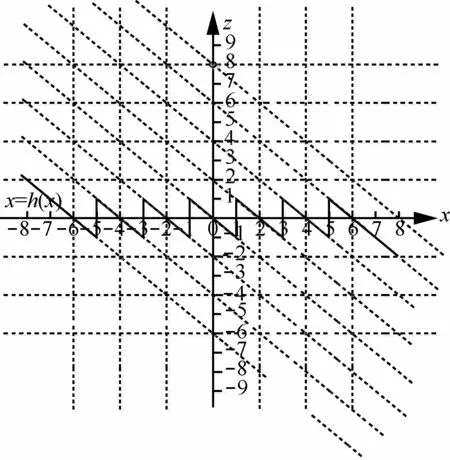
图3 系统(3)对应指标2的鞍焦平衡点分布
由于所得的雅可比矩阵是一个固定矩阵,故该矩阵与平衡点的具体数值无关,其对应的特征多项式为
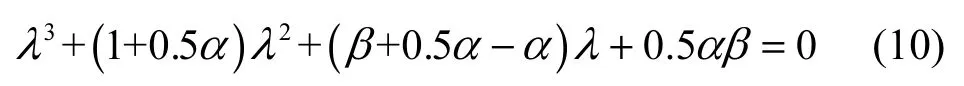
令α= 10,β= 16得出平衡点处矩阵的特征值分别为:γ= − 6.277 7,λ1= 0.138 9 + j3.567 1,λ2= 0.138 9 − j3.567 1。γ为负实根,λ1与λ2是一对具有正实部的共轭复根。因此,系统(3)的平衡点是不稳定的鞍焦点,满足Shilnikov定理,即对于三阶自治系统平衡点的特征值γ和σ± jw,若γσ< 0且|γ|>|σ|,则σ满足系统的矢量场产生混沌的鞍焦点条件,从而在理论上证明了系统(3)存在混沌的可能性。
3.4 Lyapunov指数、维数
Lyapunov指数是衡量系统动力学特性的一个重要定量指标,它表征了系统在相空间中相邻轨道间收敛或发散的平均指数率。本文利用三阶Runge-Kutta方法数值模拟求解新系统,从而得到系统的3个Lyapunov指数,如图4所示。其中,λL1=0.255 3,λL2= 0.007 8,λL3= − 6.263 3。由混沌理论可知,若系统是混沌的,则必须满足以下条件:1) 至少存在一个正的Lyapunov指数;2) 存在一个实数λi逼近于0;3) 所有Lyapunov指数之和为负。由λL1、λL2、λL3可得该系统是混沌的,则其对应的Lyapunov维数为
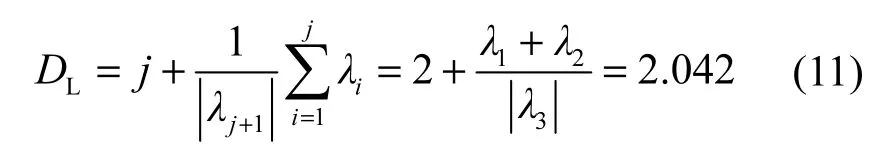
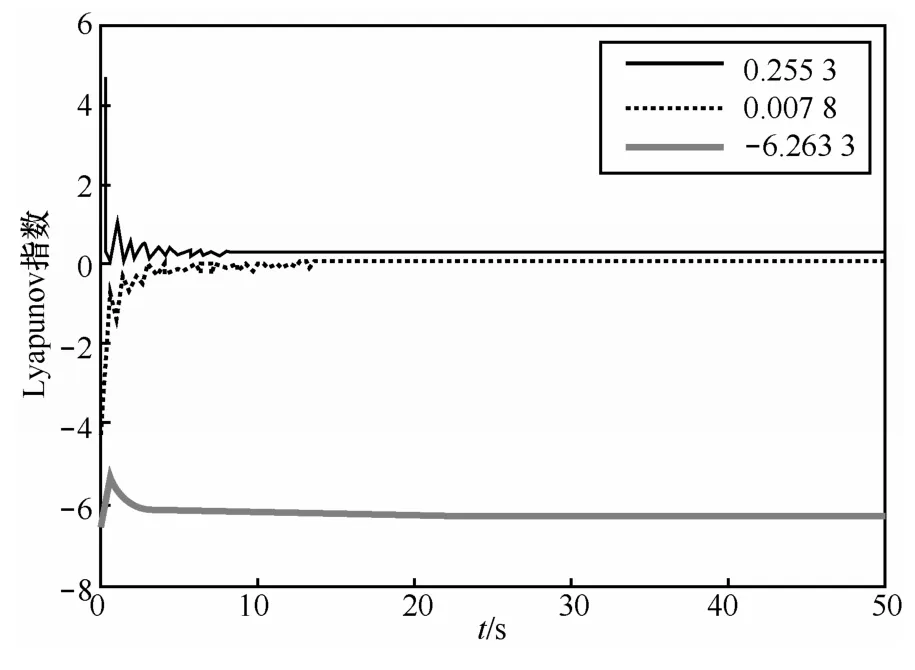
图4 系统(3)的Lyapunov指数谱
Lyapunov维数介于2到3之间,从而验证了该系统为混沌系统。
3.5 时域波形、功率谱、分岔图及最大Lyapunov指数谱
系统(3)产生的时间序列具有一定的非周期性,而且对初始值的改变也极为敏感。即使只对初始值中的某一个数做细微的调整,得到的时域波形也会有很大差别,如图5所示。这里将初始值分别取为(2,0.5,0.005)和(2,0.5,0.006)。在0 <t< 20 s时,两曲线没有明显的区别,而当t> 20 s时,两曲线表现出截然不同的时间演化曲线,这表明了系统的运动状态对初始条件极为敏感,其相轨道在一定的区域内无限填充或游荡,具有典型的非周期特性。图6为系统的功率谱,功率谱是研究系统从分岔走向混沌的重要方法。其中,周期运动对应尖锋,而混沌的特征则是谱中出现“噪声背景”和“尖峰”。不难看出,该系统在一定频率范围内是连续谱,并表现出明显的非周期混沌特性。由于该拉伸式多涡卷混沌系统的结构十分复杂,无法刻画出较大参数变化范围内的分岔图。因此,图7重点分析了参数β在[16,16.1]上的局部分岔结构以及对应的最大Lyapunov指数谱,其中,α= 10。混沌结构一般包含3种状态:稳态、周期态和混沌态。当系统处于稳态或周期态时,其对应的分岔图由一条或多条连续的线构成。而当系统进入混沌态时,在分岔图中存在无数个类随机点。通过观察不难发现,与一般的混沌结构不同,系统(3)的分岔图在该区间展现出多个分岔结构,并且均处于混沌态。与此同时其对应的最大Lyapunov指数在[16,16.1]范围内也基本为正数,从而进一步证明了新系统在该区间内是混沌的。
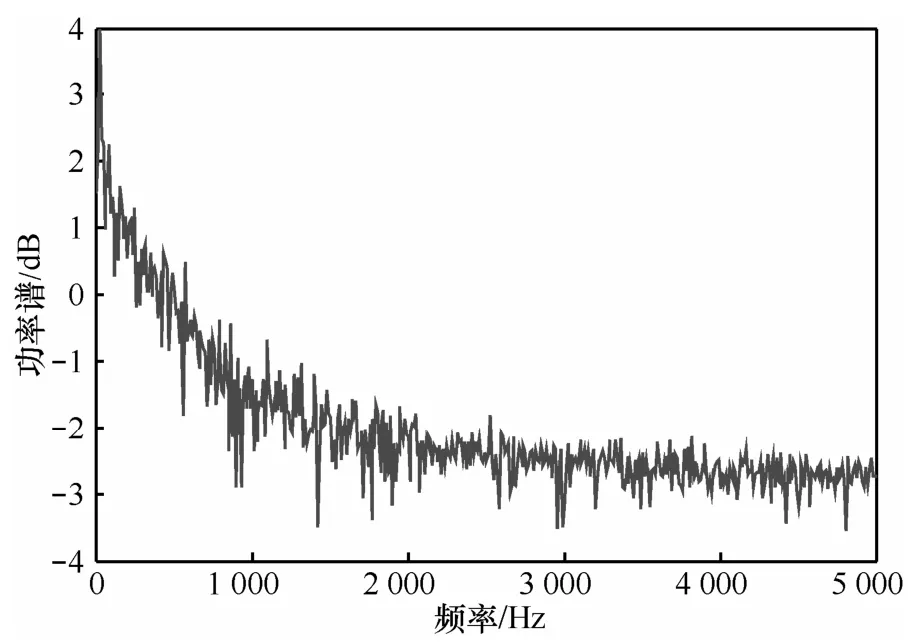
图6 系统(3)的功率谱
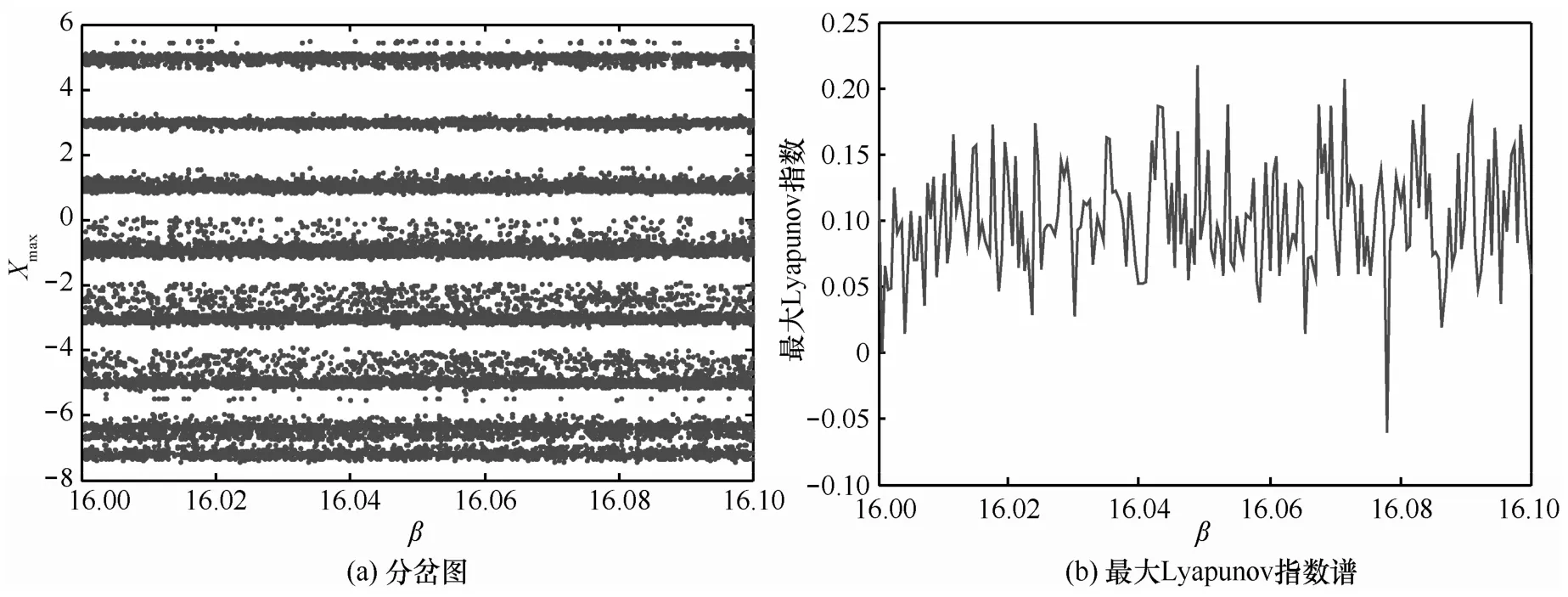
图7 系统(3)随β变化的分岔图和最大Lyapunov指数谱
由以上分析可知,本文所提出的新型多涡卷混沌系统,除了对初始值的取值极为敏感之外,参数α、β、γ1和γ2对系统状态影响也很大。不同的参数选取,会使该混沌系统的结构发生变化,从“半涡卷”混沌变为涡卷混沌。由于该混沌系统对初始值的极端敏感依赖性,同时还可以提供数量众多、非相关、类随机而又确定性的混沌信号。所以这种拉伸式多涡卷混沌吸引子在实际保密通信系统中具有一定的开发潜力。
4 电路仿真
混沌系统中最简单最直接的物理模型就是电路实现,许多混沌系统的动力学行为都是在电路上得到了验证。本文利用PSPICE软件对该系统进行了电路仿真。考虑到状态变量的取值应在集成电路允许的工作电压范围内,结合图2的相图大小,首先对其进行等比例压缩变换,这里将混沌系统均匀压缩至原系统的。然后采用线性电阻R、线性电容C以及运算放大器TL082实现了系统(3)的物理模型。其中,运放选取的电压值为±15 V,饱和值Vsat=±13.5 V。此外,τ0=R0C0既是时间尺度变化因子,也是积分器的积分常数。利用这一特性,可改变混沌信号在时域中变化的快慢以及混沌信号频谱的分布范围,所以合理地选择时间尺度变换因子的大小,对于混沌电路的设计以及实现至关重要。这里变换因子选取R24=R34=R42= 60 kΩ,C1=C2=C3= 210 nF。根据系统(3)设计的电路如图8所示。
−f(x)、−d(z)和h(x)是产生阶跃函数的发生电路。系统(3)等比例压缩后,由电路的基本理论及各个组件的特性,得到的电路方程为
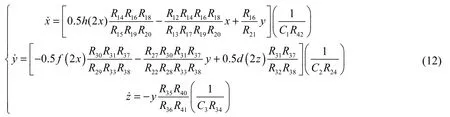
式(12)与式(3)对照,可得
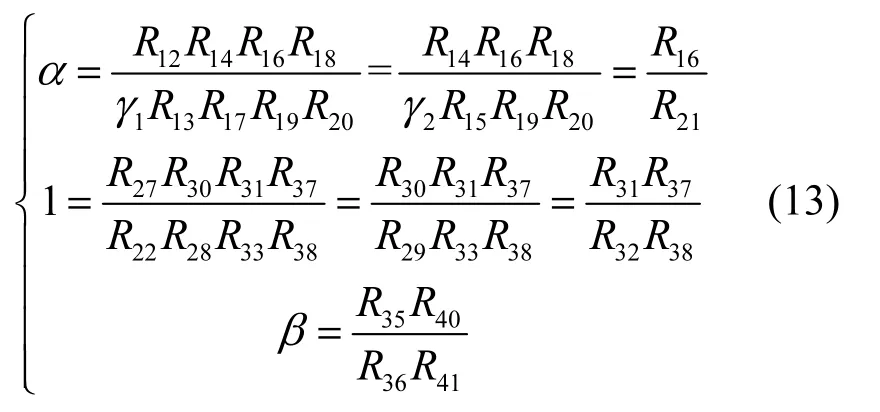
令α= 10,β= 16,N= 3。其中,R1~R6、R8~R11、R44、R45、R47、R50和R53均为13.5 kΩ,R15、R17、R20、R21、R26、R36、R39和R43均为10 kΩ,R14= 5 kΩ,R35= 160 kΩ,R7=R48= 0.94 kΩ,剩余电阻均为100 kΩ。根据图2的参数关系对R15和R17的取值进行修改。考虑到仿真时间、饱和度以及初值对仿真结果的影响,本次电路实验从3时刻开始,最大仿真步长设置为0.01 s,仿真时间为50 s,得到系统(3)的电路仿真结果如图9所示。可以观察到电路结果与数值仿真基本保持一致,从而验证了混沌系统在电路中的存在性。
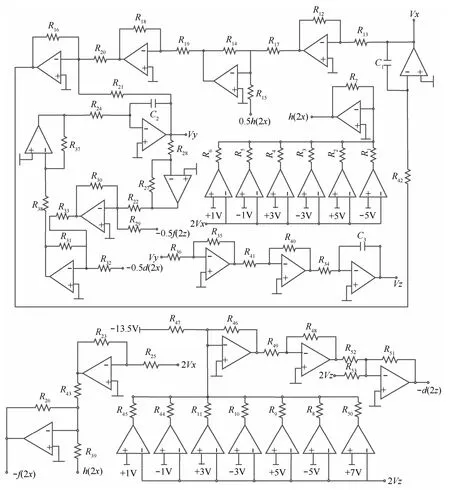
图8 系统(3)的电路原理
5 混沌系统的同步及保密通信
5.1 拉伸式多涡卷混沌系统的同步
目前,混沌主要以2种方式应用于保密通信中,一种是混沌同步;另一种是混沌映射。其中,混沌同步通过混沌载体流对接收端的驱动作用来实现,该加密方式是一种动态加密,并且处理速度和密钥长度无关。即使密文也参与了密钥流的生成,短时间内传输错误也不会引起错误扩散。因此,这种算法效率很高,特别适用于实时信号处理。同时,传统加密通信中经常采用频谱分析法对其进行破译,但此种方法对混沌加密后的传输信号却没有太大作用,主要是因为混沌传输信号具有类似噪声的宽频谱特点,传统方法无法基于频谱分析得到有用信息。另外,传统加密方式生成的加密信号与原始信号之间存在一定的相关性,这对实际保密通信系统的安全性是一个非常不利的因素。而对混沌保密通信来说,只要选取适当的密文变换函数,那么生成的加密信号就是遍历的、均匀分布的,该信号与原始信号之间的互相关性趋于零。所以人们越来越重视混沌系统在实际通信应用中的潜力。
基于以上混沌保密通信的研究成果,本文提出的拉伸式多涡卷混沌系统,结构复杂,且由于密钥参数的变化形成复杂多变的混沌系统,可以大大提高实际通信的保密效果和破解难度。为实现该系统的混沌同步,将系统(3)的驱动系统和响应系统的状态向量,分别取(x1,y1,z1)和(x2,y2,z2),则驱动系统的状态方程表示为
响应系统的状态方程表示为
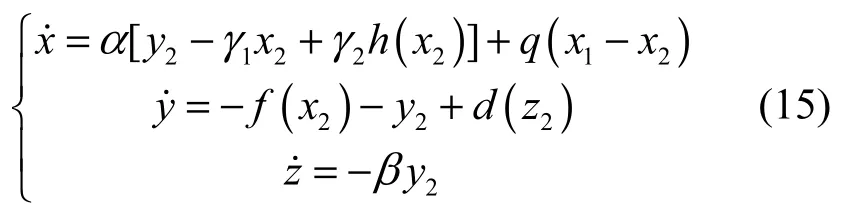
其中,q为耦合系数。
定义同步误差为
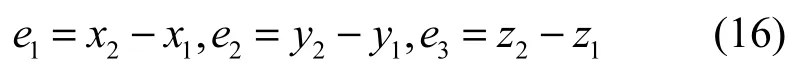
结合式(2)、式(4)和式(5),得到如下的同步误差系统。
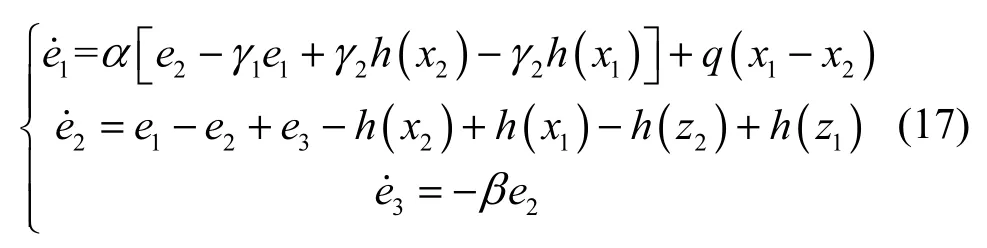
定理1对于混沌系统,当控制器取u = −qe1且q足够大时,得到的闭环系统是渐近稳定的,从而实现系统(14)和系统(15)之间的渐近同步。
证明上式非线性函数h(x)是Lipschitz函数,驱动系统和响应系统中的非线性部分,对于任意实数x1和x2,均满足Lipschitz条件
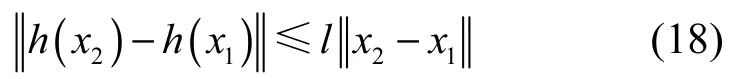
且l ≥ 0。
进而,对任意实数x1、x2和e1,都有
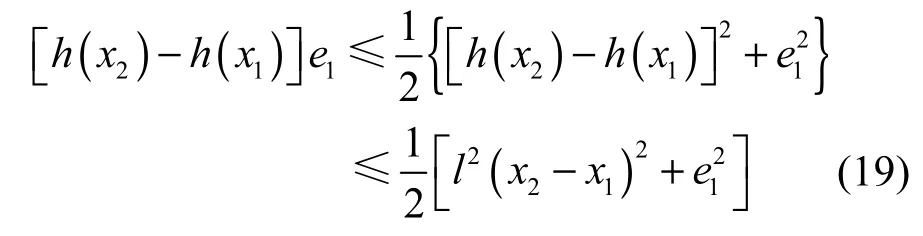
将控制器u = −qe1和式(19)代入式(17)中,得误差系统
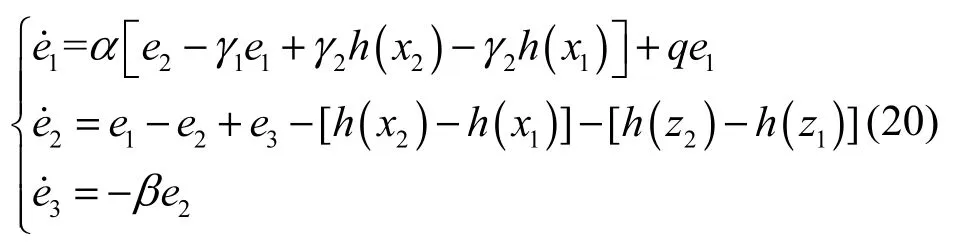
这里选取Lyapunov函数
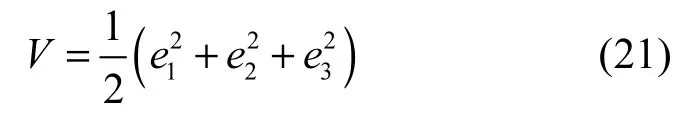
将V沿系统(3)的轨迹对时间t求导,得
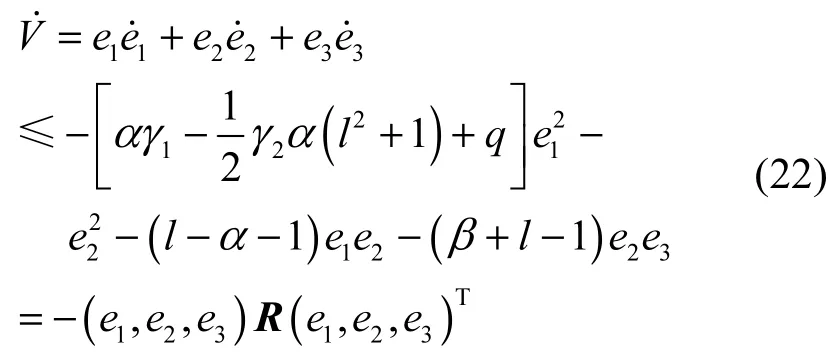
其中,
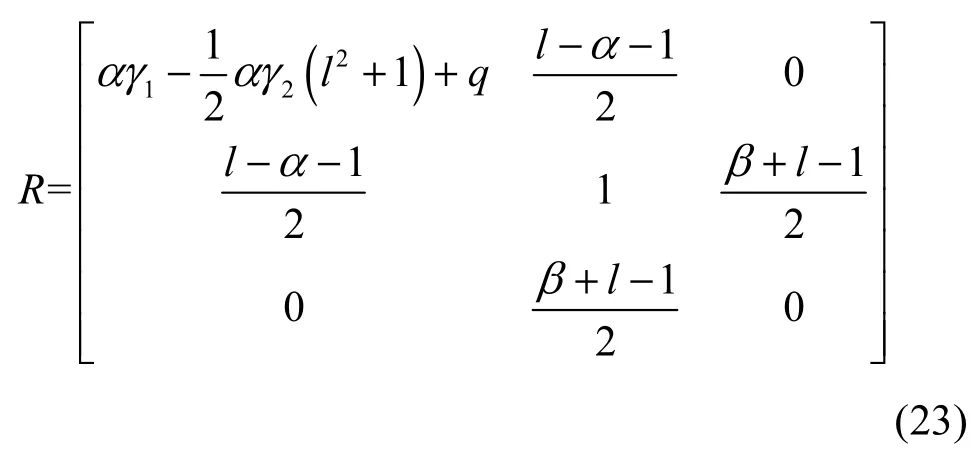
根据其对应的特征方程可得,只要选取适当的增益q,使
由Lyapunov稳定性理论可知,闭环系统(17)是渐近稳定的,从而证明了系统(14)和系统(15)可以实现同步。
5.2 数值仿真
利用Matlab,将系统参数分别设为:α = 10,β = 16,γ1= γ2= 0.50,N = 3,其中,系统(14)和系统(15)的初始条件为 (2,0.5,0.005)、(0.2,0.54,0.05)。令耦合系数q=10,在线性反馈控制下,驱动系统和响应系统的同步误差仿真曲线如图10所示。可以看出,经过一个暂态过程后系统(20)的误差变量e1、e2、e3全部趋于0,这说明驱动系统和响应系统已达到完全同步,进而验证了线性控制器的有效性。
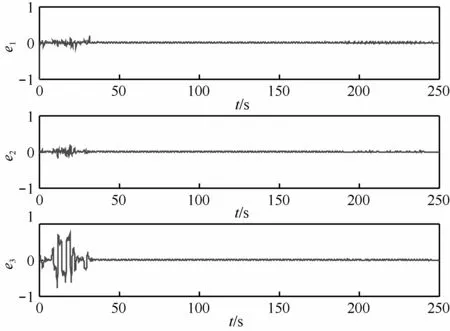
图10 驱动系统和响应系统对应的同步误差仿真
5.3 拉伸式多涡卷混沌系统在保密通信中的应用
利用以上驱动系统和响应系统的同步关系,在混沌控制的基础上进行了保密通信的应用,其加密、解密过程的原理结构如图11所示。
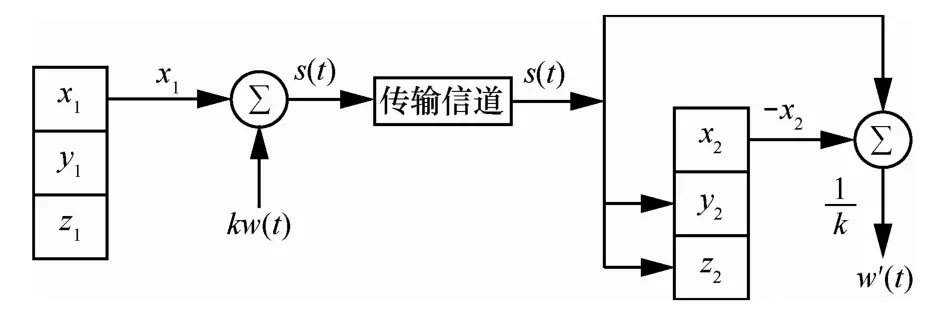
图11 新型多涡卷混沌同步系统的加密、解密原理
发射系统为
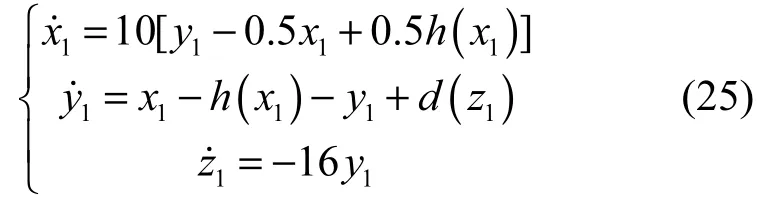
接收系统为

其中,h(x)、d(z)、s(t)分别为
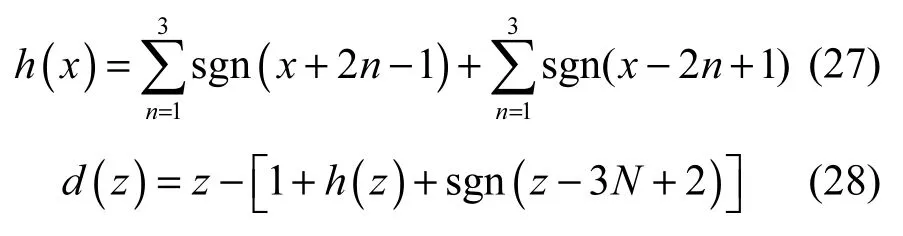
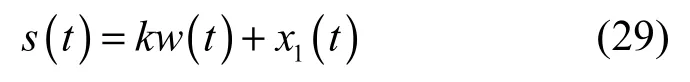
假设需要加密的信号为一段特定的数字信号w(t),由Matlab产生,如图12所示。这里系统的初始密钥为 (2,0.5,0.005) 和 (0.2,0.54,0.05),结合式(25)取q =10。在发送端将这一信号和驱动系统中的混沌信号x1叠加,并将产生的混叠信号s(t)发送到传输信道中,加密函数s(t)的选取比较灵活,可以是线性的,也可以是非线性的,可以是连续的,也可以是有断点的。本文选择了s(t) =kw(t) +x1(t)作为加密函数,采用发送端的非线性混沌信号作为密钥,将其同时发送到传输信道中,大大加强了信号的破解难度,同时,该加密函数还可以动态调整,一般地,为了对传输信号进行掩盖,传输信号的幅值不能太大,否则有用信号则不会被混沌信号很好地覆盖,故本文方案的幅值k为0.l。
与加密过程相似,解密是加密的逆过程,只要加密的过程是可逆的,解密就可以实现。混沌解密技术是将叠加的信号看成是对混沌轨迹的微扰,这种扰动将会导致系统相应的回归映射点偏离由纯净混沌系统得到的映射曲线,所以可以运用混沌同步原理,通过测量当前映射点相对纯净映射曲线的偏离程度,即可推出相应信号强度进而取出被掩盖的信号。因此,在接收端只需从s(t) 中减去受控系统产生的同步混沌信号x2(t),再扩大10倍,就可恢复出有用信号w'(t)。整个混沌同步保密通信的仿真结果,如图12~图15所示。不难发现,数字信号w(t)经过拉伸式混沌系统的加密、解密,迅速得到了当前信号w'(t),使该数字信号得到无失真传输,即w'(t)−w(t)→0,从而证明了该系统在保密通信应用中的可行性。
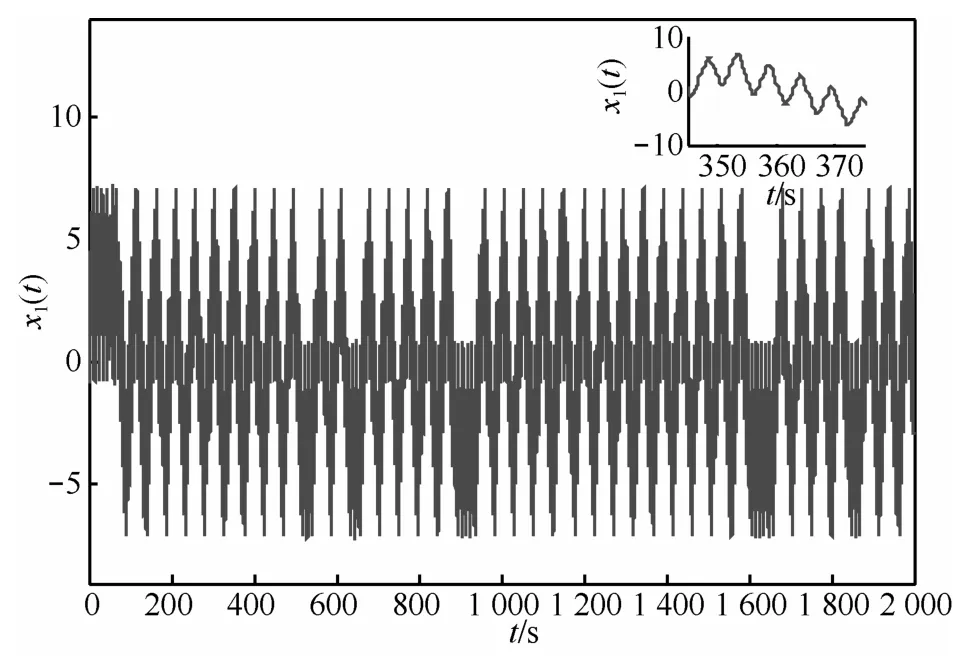
图12 加密前混沌信号x1(t)的时域波形
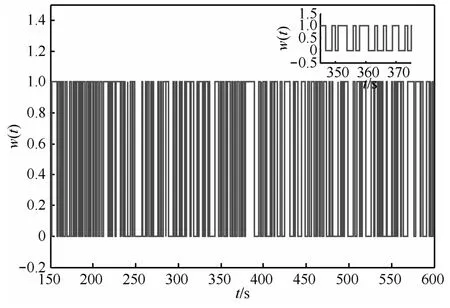
图13 数字信号w(t)的时域波形
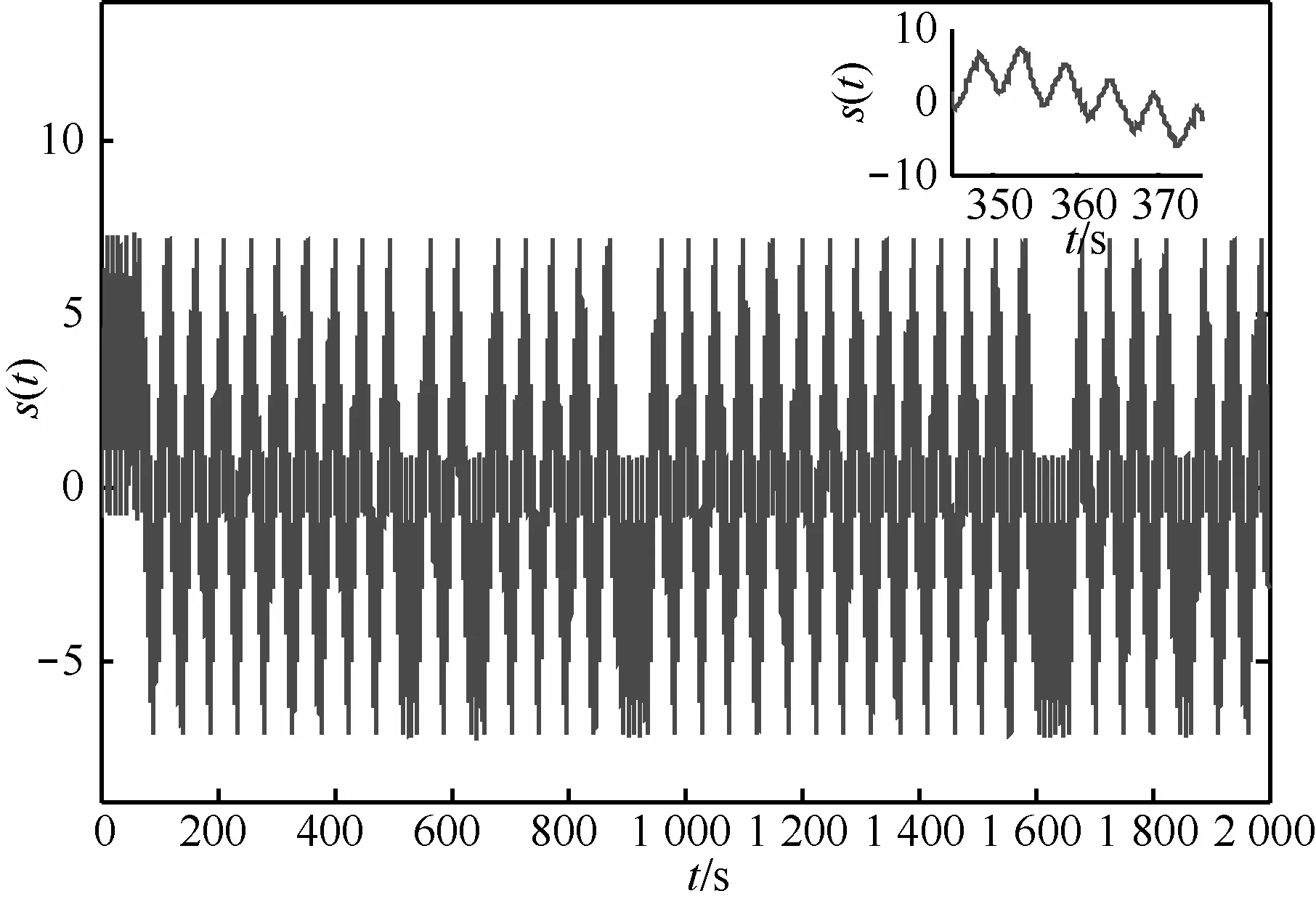
图14 加密后混沌传输信号s(t)的时域波形
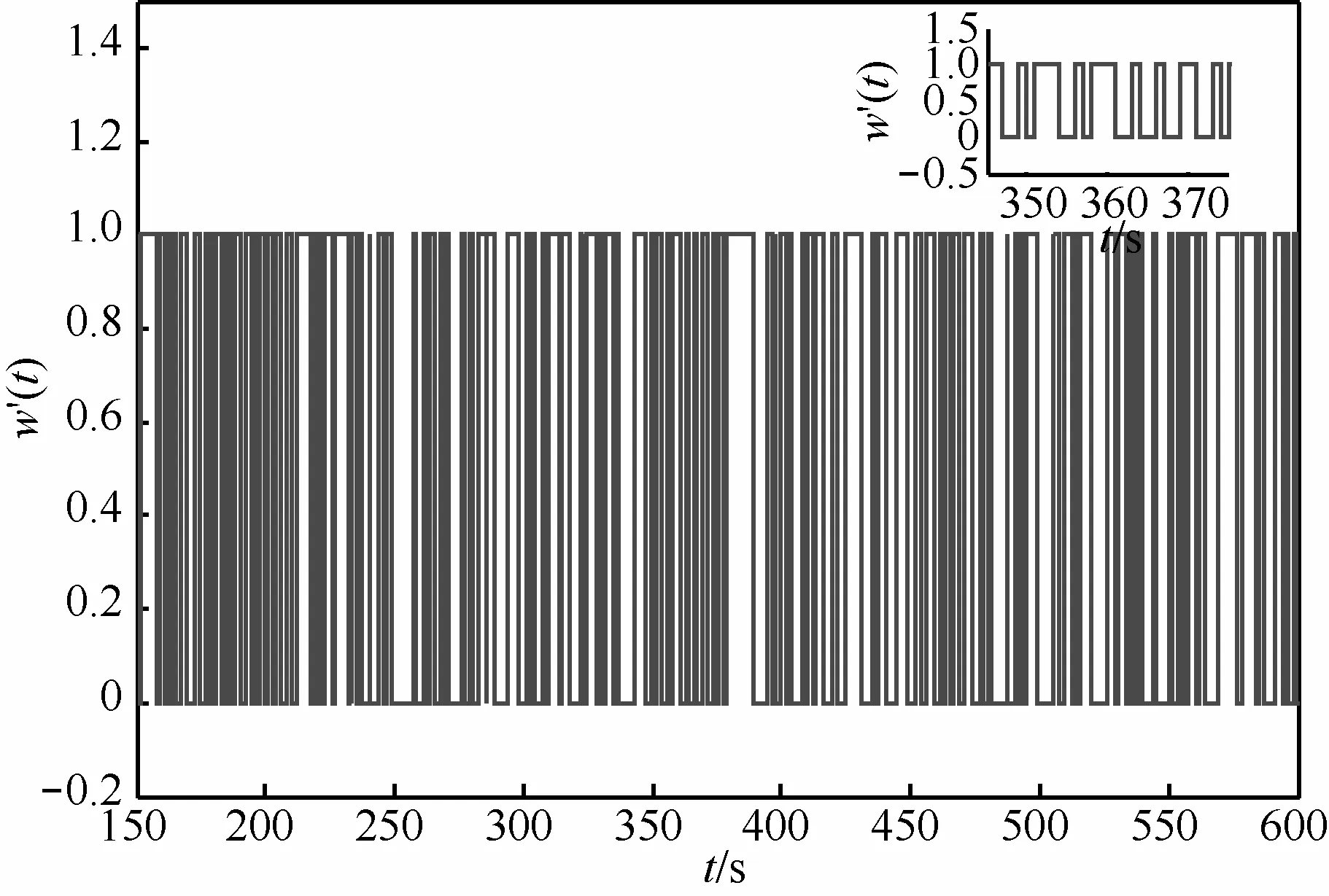
图15 解密后得到信号w'(t)的时域波形
5.4 拉伸式混沌保密通信的同步性能分析
由于混沌系统天然的初值敏感性、各态历经性和内随机性等特征共同影响着加密系统的混沌信号,稍有偏差就会对混沌序列产生很大影响,因此,混沌同步加密是一种保密性很高的方法。与传统依靠软件形成密码的方式不同,混沌加密重点依赖于系统的硬件密码,即混沌产生机制,这就使混沌加密的性能分析与传统密码学的分析研究有很大的区别[9]。结合5.3节混沌同步掩盖的加密、解密过程,本节主要从系统参数、初始密钥以及同步控制器u的选取3个方面对其进行了分析说明[30]。
5.4.1 系统参数γ对混沌同步系统性能的影响
结合2.2节中拉伸式3-D多涡卷混沌吸引子的多种混沌结构,即γ1= 0.45,γ2分别取0.47、0.49、0.51以及γ1= 0.50,γ2= 0.50,这4种情况进行加密仿真。令混沌同步加密系统误差,则其对应的误差曲线如图16所示。
由选取4种参数互不相同的混沌系统仿真结果显示,在一定的时间范围内均能完全满足同步要求。考虑到混沌结构对于系统参数的要求较高,特别是当一个系统中的多个参数同时变化时,极少能保证其产生的新型结构仍为混沌状态,而拉伸式3-D多涡卷混沌系统,却较好地实现了该多态特性。通过对比不难发现,图16(c)达到系统同步的时间最短,图16(b)对应的时间最长,可见该多涡卷混沌同步加密方式可以通过调节参数,实现4种加密系统,而同步时间的长短则需要针对不同的物理性能进行适当的选取,因此这种特性在实际加密、控制等方面应用前景较为广泛。同时图16(b)和图16(d)在t<34 s时,2个系统的误差曲线极为相似,这说明在一定范围内该多涡卷混沌系统当参数发生变化时还具有较强的顽健性。因此,将拉伸式多涡卷混沌系统应用在保密通信中,可以大大增加同步加密的选择性以及稳定性。
5.4.2 初始密钥对混沌同步系统性能的影响
当一个确定性系统的发展演化行为敏感地依赖于系统的初始条件时,则称这个系统是混沌的。混沌的这个特征暗示出:对于2个初始条件很相近的不同轨道,最终将会以指数的方式分离,只要初始条件稍微有所差别或微小扰动就会使系统的最终状态出现巨大的差异。因而,混沌系统的长期演化行为是不可预测的。5.3节正是利用该特性,将所提出的拉伸式多涡卷混沌系统运用到混沌保密系统中,实现了系统的加密、解密的整个过程。为了说明初始密钥对混沌同步系统的影响,以下对上述混沌同步加密系统进行了分析。
结合5.3节中加密、解密的应用系统,保持系统参数不变从同一个混沌同步加密系统的发送端,接收端中选取3组互不相同的初始密钥(x(0),y(0),z(0)),探究了在该条件下同步加密系统的误差曲线,如图17所示。
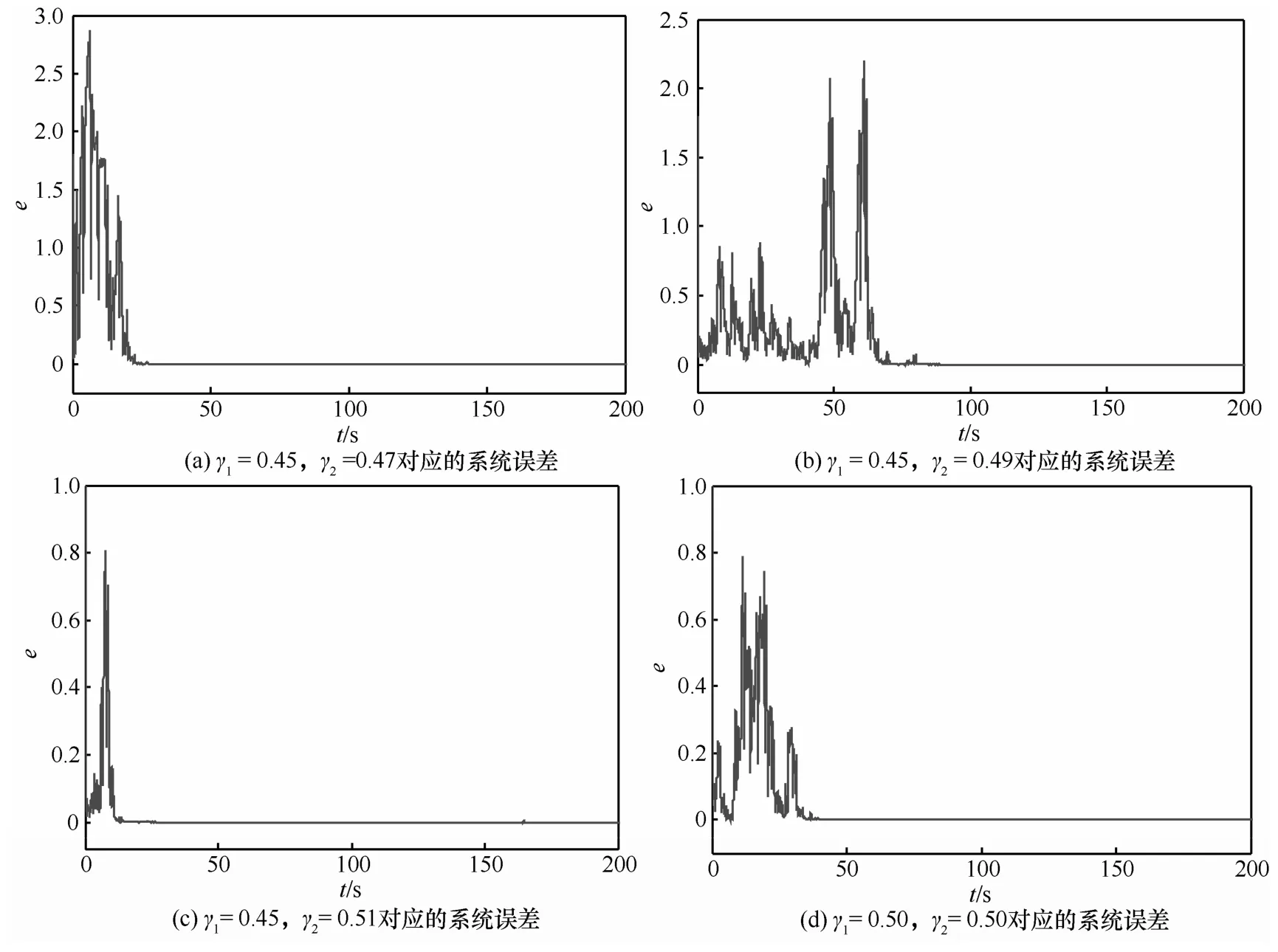
图16 γ1、γ2取不同值时,新型多涡卷混沌同步加密系统的误差曲线
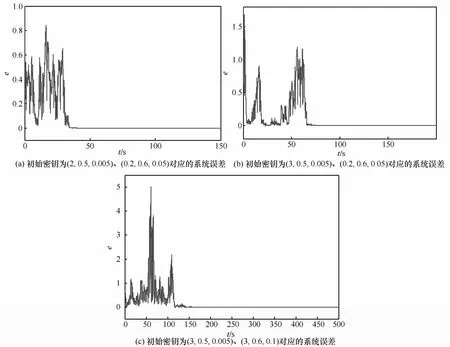
图17 发送端和接收端在不同初始密钥条件下,新型多涡卷混沌同步加密系统的误差曲线
3组初始密钥(x(0),y(0),z(0))分别为
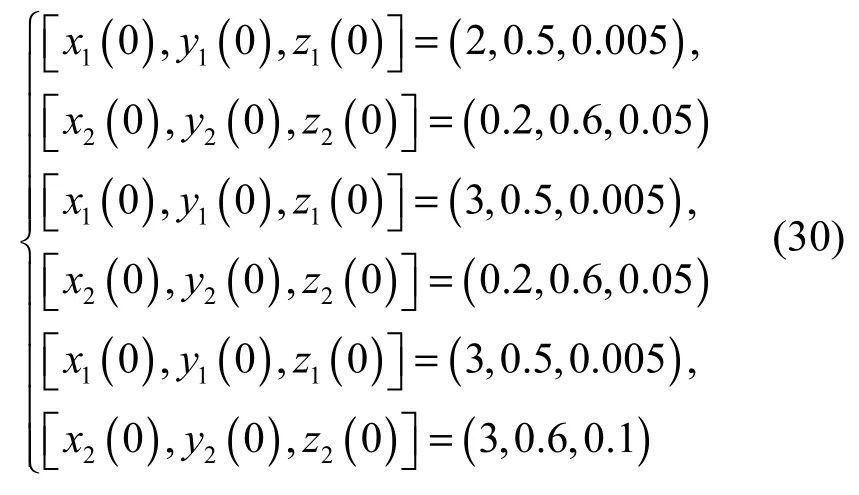
由图17可知,混沌同步加密系统的精确同步时间长度与初始条件下发送端和接收端两者的初始密钥的大小有关。当混沌系统初始密钥相差较小时,加密、解密达到系统同步所需要的时间较短,而当初始密钥相差较大时,系统同步所需要的时间也就越长。图17很好地证明了这一加密机制,随着3个初始密钥之间的差值由小变大,系统达到同步加密所需要的时间也逐渐变长。但总体来说,即使在初始密钥相差较大的情况下,也会达到令人较为满意的同步效果。可见当初始密钥发生变化时,会对系统趋于同步的时间产生一定影响,并不会改变加密系统最终的稳定状态。
5.4.3 控制器对混沌同步系统性能的影响
由于在拉伸式多涡卷混沌加密系统中,控制器u= −qe1且q的取值范围较广,为了便于理解控制器对该混沌加密系统的影响,这里利用李萨如图像及同步时域波形,对不同控制器下的同步加密系统性能进行了分析说明。
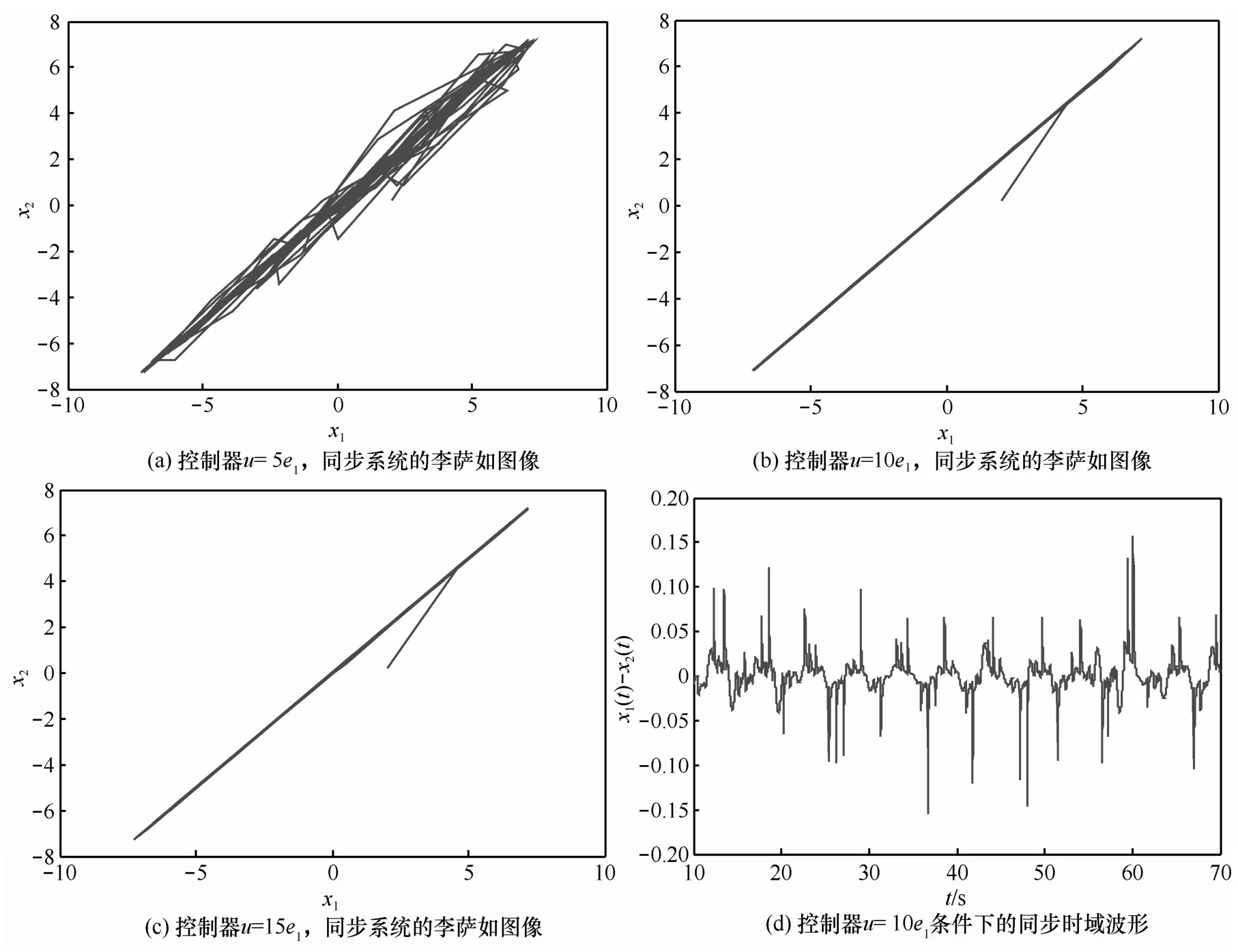
图18 不同控制器u对应的新型多涡卷混沌同步系统的李萨如图像及混沌同步的时域波形
图18中的混沌控制器分别为u= 5e1、u=10e1、u=15e1,仿真结果分别对应图18(a)、图18(b)、图18(c)。其中,γ1= 0.50,γ2= 0.50且初始密钥均为(2,0.5,0.005),(0.2,0.54,0.05)。不难看出,图18(a)由于控制器选取的不合理使系统并未达到预期的同步效果,同时还产生了大量扰动,非常不利于混沌同步加密系统的物理应用。而从图18(b)和图18(c)的李萨如图像可以看出,系统在相应控制器下达到了完美同步,由于同步加密系统的初始密钥相差较大,所以在系统刚开始加密时,存在一些偏差,随后很快实现完全同步。此外,图18还刻画了当控制器为u=10e1时,混沌同步加密系统对应的状态方程到达稳态的时域波形(如图18(d))。不难发现,当混沌驱动系统和响应系统实现同步时所产生的混沌时间序列并非完全一样,两者之间的稳态在零点附近存在微弱波动。这是由于初始密钥之间的微小差异一直伴随着混沌序列的整个过程,但对整个信号的正确加密、解密并没有太大影响。
综上所述,将拉伸式3-D多涡卷混沌吸引子应用在混沌保密通信中主要具有以下3点优势:1) 多变的系统参数,能够使其在同步加密中有更多可选的混沌空间,更加符合在实际应用中多变的系统环境;2) 由于多涡卷混沌同步加密信号存在初始密钥的敏感性、长期不可预测性、隐蔽性及高度复杂性等特性,即使破译者截获了其中的加密信息,在不知情系统的驱动——响应状态方程的情况下几乎不可能破译该密文,因而在信号传输过程中并不需要特殊的保密通道,特别适用于保密通信;3) 混沌同步加密系统中的控制器是不唯一的,从而进一步增强了破译者的破译难度。因此,拉伸式多涡卷混沌同步加密系统,无论在科研领域还是实际工程中都具有非常很好的研究价值和应用前景。
6 结束语
本文基于Chua电路的非线性特性,提出了一种拉伸式3-D多涡卷混沌系统。其复杂多变的混沌结构为多涡卷混沌吸引子的研究提供了新的思路。通过平衡点、分岔图、最大Lyapunov指数等,分析了该混沌系统的动力学特性。同时,结合混沌电路设计的理论研究,从参数的选取、电路调节到最后的仿真,实现了该混沌吸引子的电路仿真,很好地验证了系统电路的可行性。最后,采用单向耦合法实现了驱动系统与响应系统的同步,并结合混沌掩盖保密通信的具体实例和数值模拟进一步验证了所给方案的有效性。这对于多涡卷混沌系统在保密通信的研究和实际应用,具有一定的促进作用。
[1]LORENZ E N.Deterministic nonperiodic flow[J].Journal of the Atmospheric Sciences,1963,20(2):130-141.
[2]KOCAREV L,HALLE K S,ECKERT K.Experimental demonstration of secure communications via chaotic synchronization[J].International Journal of Bifurcation and Chaos,1992,2(3):709-713.
[3]LU J H,YU X H,CHEN G R.Chaos synchronization of general complex networks dynamical[J].Physica A,2004,334(1):281-302.
[4]TIMMER J,RUST H,HORBELT W,et al.Parametric,nonparametric and parametric modelling of a chaotic circuit time series[J].Physics Letters A,2000,274(3):123-134.
[5]PECORA L M,CARROLL T L.Synchronization in chaotic systems[J].Phys Rev Lett,1900,64(8):821-824.
[6]王兴元,段朝锋.基于线性状态观测器的混沌同步及其在保密通信中的应用[J].通信学报,2005,26(6):105-111.WANG X Y,DUAN C F.Observer based chaos synchronization and its application to secure communication[J].Journal on Communications,2005,26(6):105-111.
[7]WANG X Y,LI X G.Feedback control of Liu chaotic dynamical system[J].International Journal of Modern Physics B,2010,24(3):397-404.
[8]闵国旗,王丽丹,段书凯.离子迁移忆阻混沌电路及其在语音保密通信中的应用[J].物理学报,2015,64(21):210507.MIN G Q,WANG L D,DUAN S K.The chaotic circuit of ion migration memristor and its application in the voice secure communication[J].Acta Phys Sin,2015,64(21):210507.
[9]王兴元.混沌系统的同步及在保密通信中的应用[M].北京:科学出版社,2012:16-80.WANG X Y.The synchronization of chaotic system and its application in secure communication[M].Beijing:Science Press,2012:16-80.
[10]CHEN G,UETA T.Yet another chaotic attractor[J].International Journal of Bifurcation and Chaos,1999,9(7):1465-1466.
[11]YALCIN M E.Multi-scroll and hyper-cube attractors from a general jerk circuit using Josephson junctions[J].Chaos,Solitons &Fractals,2007,34(5):1659-1666.
[12]LU J,CHEN G.A new chaotic attractor coined[J].International Journal of Bifurcation and Chaos,2002,12(03):659-661.
[13]MATSUMOTO T,CHUA L O,TANAKA S.Simplest chaotic nonautonomous circuit[J].Physical Review A,1984,30(2):1155-1157.
[14]BILOTTA E,PANTANO P,STRANGES F.A gallery of Chua attractors:part I[J].International Journal of Bifurcation and Chaos,2007,17(1):1-60.
[15]SUYKENS J A K,CHUA L O.N-double scroll hyper-cubes in 1-D CNNS[J].International Journal of Bifurcation and Chaos,1997,7(08):1873-1885.
[16]LAMARQUE C H,JANIN O,AWREJCEWICZ J.Chua systems with discontinuities[J].International Journal of Bifurcation and Chaos,1999,9(4):591-616.
[17]MAHLA A I,BADAN PALHARES Á G.Chua's circuit with a discontinuous nonlinearity[J].Journal of Circuits,Systems,and Computers,1993,3(1):231-237.
[18]SUYKENS J A K,VANDEWALLE J.Generation of n-double scrolls[J].Circuits and Systems I:Fundamental Theory and Applications,IEEE Transactions on,1993,40(11):861-867.
[19]YIN Y Z.Synchronization of chaos in a modified Chua’s circuit using continuous control[J].International Journal of Bifurcation and Chaos,1996,6(11):2101-2117.
[20]刘明华,禹思敏.多涡卷高阶广义Jerk电路[J].物理学报,2006,55(11):5707-5713.LIU M H,YU S M.Multi-scroll high-order general Jerk circuits[J].Acta Phys Sin,2006,55(11):5707-5713.
[21]李亚,禹思敏,戴青云.一种新的蔡氏电路设计方法与硬件实现[J].物理学报,2006,55(8):3938-3944.LI Y,YU S M,DAI Q Y.A novel approach for Chua’s circuit design and its hardware implementation[J].Acta Phys Sin,2006,55(8):3938-3944.
[22]SAKTHIVEL G,RAJASEKAR S,THAMILMARAN K.Statistical measures and diffusion dynamics in a modified Chua’s circuit equation with multi-scroll attractors[J].International Journal of Bifurcation and Chaos,2012,22(1):1250004.
[23]TANG K S,ZHONG G Q,CHEN G.Generation of n-scroll attractors via sine function[J].IEEE Trans.Circuits Syst-I,2001,48(11):1369-1372.
[24]PENG Z,WANG C,LUO X.A novel multi-directional multi-scroll chaotic system and its CCII+ circuit implementation[J].Optik-International Journal for Light and Electron Optics,2014,125(22):6665-6671.
[25]WANG C,LUO X,WAN Z.Generation and circuit implementation of multi-block multi-directional grid multi-scroll chaotic attractors[J].Optic-International Journal for Light and Electron Optics,2014,125(22):6716-6721.
[26]毛学志,徐勇,刘建平.基于反正切的网格混沌吸引子及其保密通信[J].通信学报,2014,35(12):106-115.MAO X Z,XU Y,LIU J P.Grid chaotic attractors based on arc tangent and its secure communication[J].Journal on Communications,2014,35(12):106-115.
[27]于娜,丁群,陈红.异结构系统混沌同步及其在保密通信中的应用[J].通信学报,2007,28(10):73-78.YU N,DING Q,CHEN H.Synchronization of different structure chaotic systems and the application in secure communication[J].Journal on Communication,2007,28(10):73-78.
[28]MA Y,LI Y,JIANG X.Simulation and circuit implementation of 12-scroll chaotic system[J].Chaos,Solitons &Fractals,2015,75:127-133.
[29]LI H,WANG L,DUAN S.A memristor-based scroll chaotic system-design,analysis and circuit implementation[J].International Journal of Bifurcation and Chaos,2014,24(07):1450099.
[30]孙克辉.混沌保密通信原理与技术[M].北京:清华大学出版社,2015:58-110.SUN K H.Principle and technology of chaotic secure communication[M].Beijing:Tsinghua University Press,2015:58-110.

马均澎(1991-),男,山西运城人,西南大学硕士生,主要研究方向为混沌电路设计、非线性系统控制。

王丽丹(1976-),女,河南长垣人,西南大学教授、博士生导师,主要研究方向为人工神经网络、非线性系统与电路设计、忆阻器与忆阻系统。

段书凯(1976-),男,重庆人,西南大学教授、博士生导师,主要研究方向为智能信息处理、自动控制及检测系统。

吴洁宁(1991-),女,重庆人,西南大学硕士生,主要研究方向为忆阻混沌电路设计、复杂网络。
Design of a tensile-type 3-D multi-scroll chaotic system and its application in secure communication
MA Jun-peng,WANG Li-dan,DUAN Shu-kai,WU Jie-ning
(Chongqing Key Laboratory of Nonlinear Circuits and Intelligent Information Processing,School of Electronic and Information Engineering,Southwest University,Chongqing 400715,China)
A kind of tensile-type 3-D multi-scroll chaotic attractor based on Chua’s circuit was successfully designed.The chaos generation mechanism was studied by analyzing the symmetry and invariance,the existence of the dissipation,as well as the system equilibrium and stability.Then,some basic dynamical properties,such as Lyapunov exponents,fractal dimension,chaotic dynamical behaviors of the new chaotic system were introduced,either numerically or analytically.At the same time,the chaotic circuit of this system was realized by PSPICE.Finally,based on Lyapunov theorem and unidirectionally coupled method,the synchronization of the chaotic system has also been investigated.With this approach,the novel system can be applied to secure communication,which can achieve the purpose of covering specific signals.The experimental results are in agreement with numerical simulation results,which verifies the availability and feasibility of this method.
Chua’s circuit,secure communication,multi-scroll attractors,circuit realization
s:The National Natural Science Foundation of China (No.61372139,No.61571372),The Fundamental Research Funds for the Central Universities (No.XDJK2016A001,No.XDJK2014A009)
TP309
A
10.11959/j.issn.1000-436x.2016280
2015-10-26;
2016-09-06
王丽丹,ldwang@swu.edu.cn
资助项目(No.61372139,No.61571372);中央高校基本科研业务费专项资金资助项目(No.XDJK 2016A001,No.XDJK2014A009)

