两层和多层结构中盐指现象的数值模拟

李文婷， 李永放

(陕西师范大学 物理学与信息技术学院， 陕西 西安 710119)



两层和多层结构中盐指现象的数值模拟

李文婷， 李永放*

(陕西师范大学 物理学与信息技术学院， 陕西 西安 710119)

摘要：采用COMSOL有限元数值模拟的方法，研究了两层各自均匀溶液模型中不同参数对盐指现象的影响。结果表明，系统的热瑞利数RT、盐瑞利数RS、初始密度稳定率Rρ0均影响界面处产生的盐指现象。当RT、Rρ0增加时，盐指增长的速度会变慢，盐指的数量增多；当RS增加而Rρ0减小时，盐指增长的速度变快，盐指的数量增多；并且在RS增大到某一值(或Rρ0减小到某一值)时，盐指的性质会发生突变。进一步提出并研究了多层溶液结构模型中的盐指现象，结果表明相邻界面之间的相互作用对盐指的产生及形状有着重要的影响。

关键词:盐指； 双扩散； 有限元法； 数值模拟

盐指现象是指热且多盐的水层位于冷且低盐的水层之上时，在界面处发生盐度较大的水向下呈指状分布的现象[1]。发生在海洋系统中密度跃层的盐指被认为是热量和盐度在垂直和水平方向混合分布的重要作用机制。早在1967年Elder等人就对海洋中的这一现象进行了研究[2]。在大气系统中，由于空气同样存在密度梯度，因此形成的对流与海水中的对流有相似的现象[3]，人们利用这方面的研究制造了纹影摄影设备，该技术在军事领域得到了应用[4]。此外，人们还发现在低质量恒星以及星体内部的岩浆中因热对流等原因产生的盐指现象，并对其进行了研究[5-7]。

在20世纪60年代中期，人们第一次在实验室观察到了盐指现象，之后研究了盐指的各种特性和产生机制[8-10]。但由于热扩散的迅速性以及当时的观测仪器精确度的制约，有关这一现象的产生机制在当时还不能被确定。随着计算机技术的发展，在20世纪80年代后，人们开始利用计算机对盐指现象进行了一系列的数值模拟，来探究这一现象的作用机理[11-17]。

数值模拟是研究盐指现象的普遍方法，之前的研究大都是在某一确定参数(如瑞利数等)下对盐指形态随时间的演化研究，这涉及盐指从产生到消失的整个过程。为了更深入研究盐指产生的机理，我们忽略水平对流等作用对盐指的影响，集中研究盐指的产生和生长这两个相位阶段，分析两层和多层结构中盐指形成速度、数目(宽度)与瑞利数RT、RS和初始密度稳定率Rρ0这些无量纲参数的关系，旨在获得盐指现象的普遍性规律。

1 模型与方法

1.1模型简介

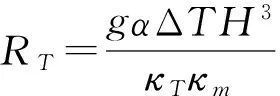
1.2方程与参数

如图1所示，定义水平向右的方向为x轴正方向，与水平方向垂直的竖直向上方向为y轴。则二维结构的盐指数值模拟方程就可以表达为如下三个方程

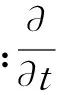
(1)

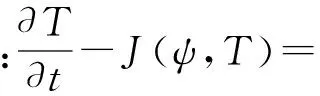
(2)

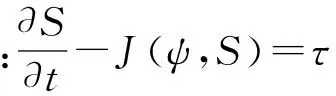
(3)

1.3模拟方法及COMSOL设置

COMSOL Multiphysics是以有限元法为基础的多物理场建模与分析的数值模拟仿真软件。其优势是可以设置多个物理场，通过耦合参数模拟复杂的物理环境。对于单场问题，通过求解偏微分方程，而对于多场问题，需通过求解偏微分方程组。模拟的一般步骤见图2。

由于该研究的过程涉及流体流动、热传导、盐扩散3个物理过程，分别对应3个偏微分方程。所以在模拟中，设置了3个物理场：(1) 用不可压缩的Navier-Stokes场来模拟流体流动，计算流体场各点的速度u、v。将涡量方程与模型场的默认方程进行对比，将差异项用体积力的方式修正，所以在不可压缩的Navier-Stokes场设置中，除了一般设置外我们加入了y方向的体积力，即

Fy=αgρTΔT-βgρSΔS。

(4)

其中ρ代表水的密度，通过温度场参数T和盐度场参数S实现了三个场的耦合。(2) 用对流与传导场来模拟热量的传递，计算温度场各点的温度T。(3) 用对流与传导场来模拟盐度的扩散，计算盐度场各点的盐度S。

2 盐指现象及其形成机理

2.1盐指现象的定义

为了研究简单盐指现象的形成，设下层溶液的温度Tb=273.15 K，盐度Sb=0.015 g/kg(除特殊说明外，后文中的Tb、Sb均不变)，上下层温度差ΔT=0.15 K，盐度差ΔS=0.03 g/kg，热瑞利数RT=7.09×106, 盐瑞利数RS=5.32×106,初始密度稳定率Rρ0=1.33。在此情况下，上层的溶液温度高、盐度高，下层的溶液温度低、盐度低。经过4 000 s之后，其温度和盐度的分布图如图3所示。只有在盐度的分布图中，可以明显观察到上下两层溶液以手指状的图案相互扩散的现象，而温度图中并没有出现这种瘦长的手指图案。可以看出当热的溶液处在上层时，双扩散中的热量扩散是线性的传递过程，而在温度图的同一水平位置的不均匀分布即图中的波动，是由于盐度的扩散所引起的扰动。因此，我们所说的盐指是指盐度在溶液中的指状分布，面的讨论中，除了特殊说明外，我们都用盐度分布图来讨论盐指现象。

2.2盐指现象的过程

上面产生盐指的模拟中，我们假设上层是热的盐度高的溶液，而下层则是冷的盐度低的溶液，也就是说，上下两层溶液同时存在着温度差和盐度差。为了理解盐指产生的过程以及机理，分别采用下面4组参数设置：(a)ΔT=0.15 K，ΔS=0 g/kg；(b)ΔT=0 K，ΔS=0.03 g/kg；(c)ΔT=-0.15 K，ΔS=0 g/kg；(d)ΔT=0 K，ΔS=- 0.03 g/kg；其中的负号表示上层的温度或盐度比下层低。计算结果如图4所示，其中图4a、c为温度分布图，图4b、d为盐度分布图。

对于图4a和c而言，两层都没有盐度差，温度差符号相反。图4a在t=4 000 s时得到的只是简单均匀的热扩散现象，而图4c在t=300 s时候出现了相互扩散的指状图案，这是由于图4a中初始状态热溶液已经位于上层时，便没有了因为阿基米德力引起的对流，因而只存在简单的热传递现象；而图4c中初始状态热的溶液位于下层，热的溶液受到阿基米德力的作用，有向上运动的趋势，一旦有一个位置出现了向上的微小对流，便会被放大，而紧邻的旁边位置，冷的溶液便会出现下沉，从而形成了上下层溶液相互交替分布的指状图案的现象。对于图4b

和d而言，上下层间都没有温度差，盐度差符号相反。图4b在t=1 000 s时就形成了明显的盐指现象，而图4d在t=4 000 s时只在分界面附近有微小的均匀扩散现象。这是由于盐度较大的溶液在重力场的作用下，会出现向下流动的趋势。所以盐度高的溶液处在上层的图4b出现了指状分布的现象，而盐度高的溶液处在下层的图4d则只是简单的分子扩散现象。同样是简单扩散，因为温度扩散系数κT比盐度扩散系数κS大，所以同样的时间，图4a的扩散要比图4d的扩散明显。并且图4b和c出现明显的指状扩散图案的时间都要比图3中的结果短很多。

由于阿基米德力和重力的作用，热的溶液有向上流动的趋势，而盐度高的溶液有向下流动的趋势。当上层的溶液温度和盐度都高于下层的溶液时，向上流动和向下流动的趋势同时存在于上下层的交界面处，这样两种趋势博弈的结果，进而产生了盐指现象。

3参数对两层结构中盐指现象的影响

当ΔT=0.05 K，ΔS=0.03 g/kg，此时系统热瑞利数RT=2.36×106，盐瑞利数RS=5.32×106，初始密度稳定率Rρ0=0.44(图5a)时，到了t=3 000 s出现了明显的盐指图案，在模拟区域范围内指状的扩散图案中的盐指数目比较少；而当ΔT=0.75 K，ΔS=0.075 g/kg，此时系统热瑞利数RT=3.54×107、盐瑞利数RS=1.33×107、初始密度稳定率Rρ0=2.67(图5b)时，在t=1 350 s时就出现了明显的盐指图案，且指状扩散图案中的盐指数量很大；所以，在不同瑞利数和初始密度稳定率下，盐指图案的差异主要在于形成明显盐指的时间和形成的指状扩散图案的盐指数量(或盐指的宽度)。为了进一步研究热瑞利数、盐瑞利数及初始密度稳定率对于盐指现象的具体影响，分别模拟了盐瑞利数不变、热瑞利数变化时以及热瑞利数不变、盐瑞利数变化时的盐指现象。进而研究参数对盐指的增长速度和指状扩散图案中盐指数量的影响。

3.1热瑞利数对盐指现象的影响

为了得到统一的结果，我们规定形成明显盐指的标志为盐指的平均高度达到标准长度(标准长度在每幅图中以黑色线条标出)，盐指数量n指向上和向下扩散形成的盐指总个数，其最小计数单位为0.5。边界处出现长度达到标准长度，但宽度为中间盐指宽度一半的盐指记作0.5个，其余正常计数。用tc表示明显盐指出现的时间。

固定RS=5.32×106(ΔS=0.03 g/kg)，变化RT(ΔT从0.150 K到0.525 K，每间隔0.075 K)选取共6组数值，计算明显盐指图案的形成时间以及盐度分布图，结果如图6所示，并通过前面的规定将结果整理成表2。图6中a—f分别对应RT=7.09×106、1.06×107、1.42×107、1.77×107、2.13×107以及2.48×107的情况。可以看出，随着温度差的增大，tc快速增加，n缓慢增加，且都大致线性增加。

tc的增大意味着盐指形成得更为缓慢，盐指的增长速度更小。从2.2的讨论中可以知道，热的溶液向上流动的趋势会阻碍重的盐水向下流动。所以当RT增加时，热效应对于盐度扩散的阻碍作用会更强，相应的盐指形成自然也会变慢；同时，由于盐指达到标准长度的时间较长，使得两层溶液交界面处出现了更多的微小扰动，进而被放大出现更多数目的盐指，盐指的宽度更小。

3.2盐瑞利数对盐指现象的影响

固定RT=1.42×107(ΔT=0. 3 K)，变化RS(ΔS从0.035 g/kg到0.060 g/kg，每间隔0.015 g/kg)选取共6组数值，同样地计算了明显盐指图案的形成时间以及盐度分布图，结果如图7所示。在图7中，由于每一幅图中上下层的盐度差并不相同，为了方便比较，将每一幅图盐度标尺的最大值St设为St=(Tb+ΔS+ 0.015)g/kg。图7中a—f分别对应RS=6.20×106、7.09×106、7.97×106、8.86×106、9.75×106以及1.06×107的情况。相应的St为0.065、0.070、0.075、0.080、0.085以及0.090 g/kg。同样将结果整理成表3。

从结果可以看到，当系统热瑞利数恒定，盐瑞利数增大时，产生的盐指数量逐渐增多，但产生明显盐指的时间越来越短。而且尽管产生盐指的数量也在增多，但增加的速度却不一样。在表3中，盐指的数量基本上是线性增加，而该结果中，盐指的数量在开始阶段并不增加，RS=8.86×106之后才急速增加。从盐度图中可以看得更明显，虽然表2和表3中最后一个结果的盐指数量相同，但从图7中的后几幅图看，盐指的数量增加得很快。

与热瑞利数不同，在盐瑞利数增大的过程中我们看到，盐指产生的速度明显加快。这是因为在热瑞利数恒定的情况下，热效应对于盐指向下扩散的阻碍不变，当盐瑞利数变大时，因盐度差而引起的向下扩散作用慢慢变强，所以产生盐指的速度越来越快。依照这种分析，当盐指形成的时间变短，两层溶液交界处产生的微小扰动会变少，相应地产生盐指的数量也会相应地减少，但得到的结果却是产生盐指的数量在增加。仔细分析，可以发现盐指数量在盐瑞利数较小时并不增加，而在RS>8.86×106之后则快速增加；与之对应的是，盐指产生的时间在RS较小时，减小的很快，但当RS> 8.86×106之后却减小的很慢；并且在RS>8.86×106之后产生的盐指图案并不像之前的那么规则，而是有高有低，弯曲参差地排布。这样的结果说明在RS>8.86×106之后产生的盐指性质发生了变化,可能存在某种相变。

4 多层结构中的盐指现象

4.1结构

由于海洋中的盐度和温度是垂向梯度分布的，这样产生的盐指存在跨越等密度面的混合，从而影响水团与水团之间的相互作用，改变水体的温度与盐度结构，进而影响大尺度环流甚至气候变化[18]。因而，研究自然情况下的海洋盐指有重要的意义。为了更接近实际，将理想的双层溶液模型改进为同时存在多层溶液， 其结构图如图8所示。将图1中的结构总体大小不变，上下分为4层，最下层溶液的温度和盐度分别为Tb=273.15 K、Sb=0.015 g/kg。每两层间的温度差为ΔT=0.30 K，盐度差为ΔS=0.03 g/kg。

4.2层间相互作用对盐指现象的影响

图9a和b表示4层溶液在不同时间的盐度分布图。结果显示，在每两层溶液的交界处，都产生了盐指现象，并且产生的指状图案在界面两端比界面中心处要长，中心处的盐指也要比两端处的宽，不同层产生的盐指在垂直方向上近乎严格的一致。在t=7 000 s时，每层的盐指较为分明；但当t=12 000 s时，所有层的盐指互相融合，形成了整体上从底部到顶部的指状图案，且两侧的指状图案比中间的明显且规整。虽然由于结构参数上的不同，无法定义与之前的讨论相一致的明显盐指，但与图6c对比仍然可以看出，在每相邻的两层溶液间盐度差和温度差相同的情况下，多层结构对盐指的产生速度并无明显影响。

与两层结构不同的是，由于多层溶液的存在，某一界面产生的向上或向下的微小扰动会受到相邻界面状态的影响，这使得中心部位的稳定性要更强。也就是说，某一界面处的微小扰动很可能会被相邻界面(同一竖直位置)处稳定的或者相反方向微小扰动的趋势所阻碍，从而导致在界面中心处出现明显的整体指状流动比两端要难且慢；同时这也导致了不同界面盐指在竖直方向上的严格一致，因为在某一水平位置，只有相邻几个界面在同一水平位置出现一致地向上或向下的微小扰动，才能产生盐指，否则不同界面处的微小扰动会相互抵消。从图9a和b中可以看出，对于内部的3个界面来说，中间界面在中心产生的指状图案明显要弱于上下界面在中心相同位置产生的指状图案。这是因为中间界面同时受到上下界面的影响，而上下界面分别只受到中间界面的影响。同时，在多层结构中，界面处的盐指形状不再是两层结构中瘦长的直条形，而是弯曲的弧形盐指，这同样也是因为多层界面之间的相互影响，导致这种弧形的盐指更容易产生。当时间足够长时，不同层之间形成的盐指会相互融合，产生贯穿所有层从底部到顶部的指状图案。而且，多层结构模型的模拟结果与Singh等人的实验结果更为接近[17, 19]。

5 结论

本文采用COMSOL有限元数值模拟的方法，研究了两层各自均匀溶液之间的盐指现象，结果表明：在重力场中，热的溶液有向上流动的趋势，盐度大的溶液有向下流动的趋势，当热的盐度高的水层处于冷的盐度低的水层之上时，向上流动和向下流动的趋势同时存在于上下层的交界面处，这样两种趋势博弈的结果，进而产生了盐指现象。通过对相关参数的研究表明，系统的热瑞利数RT、盐瑞利数RS、初始密度稳定率Rρ0均会影响界面处产生的盐指现象。当RT、Rρ0增加时，盐指增长的速度会变慢，盐指的数量会增多；当RS增加而Rρ0减小时，盐指增长的速度会变快，盐指的数量也会增多；并且在RS增大到某一值(或Rρ0减小到某一值)时，产生的盐指的性质会发生突变。对多层溶液中盐指现象的研究表明，相邻界面间的影响使得不同界面产生的盐指在竖直方向上严格地一致，而盐指的形状变成弧形且更明显地出现在界面的两端。为了更确切地模拟自然复杂环境下的对流，下一步将对溶液存在盐度和温度梯度的模型进行研究。

参考文献：

[1] KUNZE E.A review of oceanic salt-fingering theory[J]. Progress in Oceanography, 2003, 56: 399-417.

[2] EIDE J W. Transient convection in a porous medium[J]. Journal of Fluid Mechanics, 1967, 27(3): 609-623.

[3] TURNER S. 地球物理流体动力学的发展和室内实验研究的影响[J]. 力学进展, 2000, 30(3): 457-470.

[4] SETTLES G S. Schlieren and shadowgraph techniques: visualizing phenomena in transparent media[M]. Berlin: Springer-Verlag, 2001.

[5] PAVEL A D. Numerical simulations of thermohaline convection: implications for extra-mixing in low-mass RGB stars[J]. The Astrophysical Journal, 2010, 723: 563-579.

[6] DENISSENKOV P A, MERRYFIELD J.Thermohaline mixing: does it really govern the atmospheric chemical composition of low-mass red giants[J]. The Astrophysical Journal Letters, 2011, 727: L8 (1-4).[7] SCHMITT W. The characteristics of salt fingers in a variety of fluid systems, including stellar interiors, liquid metals, oceans, and magmas[J]. Physics of Fluids, 1983, 26: 2373.

[8] BAINES P G, GILL A E. On thermohaline convection with linear gradients[J]. Journal of Fluid Mechanics, 1969, 37(2): 289-306.

[9] STERN M E. Collective instability of salt fingers[J]. Journal of Fluid Mechanics, 1969, 35(2): 209-218.

[10] TURNER J S. Salt fingers across a density interface[J]. Deep-Sea Research, 1967, 14: 599-611.

[11] VERONIS G. The role of the buoyancy layer in determining the structure of salt fingers[J]. Journal of Fluid Mechanics, 1987, 180: 327-342.

[12] WHITFIELD D W A, HOLLOWAY G, HOLYER J Y. Spectral transform simulations of finite amplitude double-diffusive instabilities in two dimensions[J]. Journal Marine Research, 1989, 47(2): 241-265.

[13] OZGOKMEN T M, ESENKOV O E, OLSON D B. A numerical study of layer formation due to fingers in double-diffusive convection in a vertically-bounded domain[J]. Journal Marine Research, 1998, 56: 463-487.

[14] 罗莹莹, 詹杰民, 李毓湘. 多孔介质中盐指现象的数值模拟[J]. 物理学报, 2008, 57(4): 2306-2313.

[15] YOSHIDA J, NAGASHIMA H. Numerical experiments on salt-finger convection[J]. Progress in Oceanography, 2003, 56: 435-459.

[16] SREENIVAS K R, SINGH O P, SRINIVASAN J. On the relationship between finger-width, velocity and fluxes in thermohaline convection[J]. Physics of Fluids, 2009, 21(2): 026601-026615.

[17] SINGH O P, SRINIVASAN J. Effect of Rayleigh numbers on the evolution of double-diffusive salt fingers[J]. Physics of Fluids, 2014, 26: 062104.

[18] SHANG X D, QI Y F, CHEN G Y, et al. Observations of upper layer turbulent mixing in the southern South China Sea[J]. Acta Oceanologica Sinica. 2015, 34(11):6-13.

[19] SINGH O P.Dynamics of double diffusive finger convection: structures and convective fluxes[D]. Bangalore: Indian Institute of Science, 2006.

〔责任编辑 李博〕

Numerical study of salt-figuring phenomenon of bilayer and multilayer structure

LI Wenting, LI Yongfang*

(School of Physics and Information Technology, Shaanxi Normal University,Xi′an 710119， Shaanxi, China)

Abstract:The finite element method numerical simulation (COMSOL) is used to investigate the influent of parameter on salt-figuring phenomenon between homogeneous layers of solution. The results show that thermal Rayleigh numbersRT、salinity Rayleigh numbersRSand initial density stability ratioRρ0all influence the salt-figuring phenomenon. When bothRTandRρ0increase, the salt-figuring pattern emerges more slowly, and the number of figuring shaped pattern increase. When theRSincrease butRρ0decrease, the salt-figuring pattern emerges more quickly, and the number of figuring shaped pattern are also increased. In addition, there are phase transition of salt-figuring property while theRSis large enough. The study of multilayer salt-figuring phenomenon shows that the affection between adjacent interface are important to the shape and growth of salt-figuring.Keywords: salt-finguring phenomenon; double diffusion; finite element method; numerical simulationPACS: 47.11.Fg, 44.25.+f

文章编号：1672-4291(2016)03-0057-07

doi:10.15983/j.cnki.jsnu.2016.03.235

收稿日期：2015-11-10

基金项目：国家自然科学基金(11474191)

*通信作者:李永放，男，教授，博士生导师。E-mail:yfl@snnu.edu.cn

中图分类号:O351.3

文献标志码:A