广义时间分数阶Hirota-Satsuma耦合KdV系统新的精确解
王苗苗, 姚若侠
(陕西师范大学 计算机科学学院, 陕西 西安 710119 )
广义时间分数阶Hirota-Satsuma耦合KdV系统新的精确解
王苗苗, 姚若侠*
(陕西师范大学 计算机科学学院, 陕西 西安 710119 )
摘要:借助复杂分数阶变换和修正的Jumarie Riemann-Liouville分数阶导数,利用一个二阶常微分方程的解,基于G′/G有限级数展开法,对耦合的非线性广义时间分数阶Hirota-Satsuma-KdV系统进行研究,由此获得了该系统的若干双曲函数和三角函数形式精确解,丰富了其精确解系。关键词: 分数阶复杂变换; 广义时间分数阶Hirota-Satsuma-KdV系统;G′/G级数展开法; Jumarie Riemann-Liouville导数; 精确解
MR subject classification: 35Q20; 35J05
近年来,分数阶微分方程[1]在众多科学领域中被用来描述某些现象,主要原因在于分数阶微积分很适合刻画具有记忆[2-3]和遗传性质的材料和过程,并对复杂系统的描述具有建模简单、参数的物理意义清楚、描述准确等优势,是物理过程与复杂力学数学建模的重要工具之一,在力学、化学、生物学、经济学等领域发挥了非常重要的作用。故此,分数阶微分方程成为研究热点,并越来越多地用于图像处理[4]、生物医学工程[4]、征收统计、地震分析[5]、粘弹性阻尼器[6]、流体力学[6]、非局部现象、 电力分形网络[7]、多孔介质、信号处理和系统识别、振动与控制[8]分数阶正弦振荡器[8-9]以及反常扩散等领域。
分数阶偏微分方程大致分为三类[10-11]:空间分数阶偏微分方程、时间分数阶偏微分方程和时间-空间分数阶偏微分方程,可以用来描述具有分形结构的多孔介质中的反常慢扩散现象,而分数阶对流-扩散方程则可以用来描述介质中流体的反常渗透现象。
由于分数阶导数具有历史依赖性与全域相关性[10-11],故分数阶微分方程求解的复杂性明显增加。但由于大部分分数阶微分方程并没有精确解析解,故Crank-Nicholson格式法、预估校正算法、线性算法、变分迭代法[11]、同伦分析法[11]、Adomian分解法[12]、同伦摄动法[12]等一系列方法被用来获得方程的数值解和近似解析解。
本文利用G′/G展开法[13]求解如下耦合的广义时间分数阶Hirota-Satsuma-KdV系统[19-20],简称HS-KdV系统的精确解
(1)
其中0<α≤1,u=u(x,t),v=v(x,t)和w=w(x,t)。
1预备知识
分数阶微积分研究中提出了许多定义,目前最常使用的3种是Caputo定义、Grunwald-Letnikov定义[14-15]和Riemann-Liouville定义。
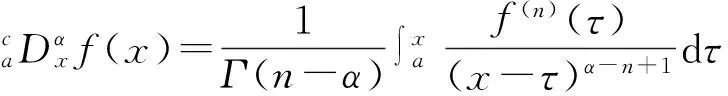
(2)
其中Γ(n-α)是伽玛函数,其广义定义为
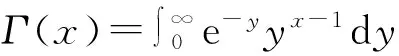
(3)
且Γ(x+1)=xΓ(x)。
当n∈N,有Γ(n)=(n-1)!。
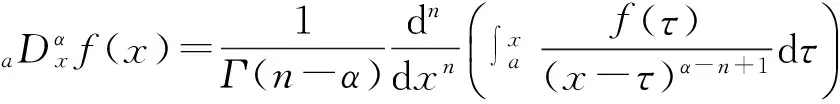
(4)
修正的Jumarie Riemann-Liouville分数阶导数[16-18]为
(5)
且其具有如下性质[18]:
dαx(t)=Γ(1+α)dx(t),
(6)
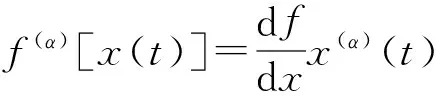
(7)
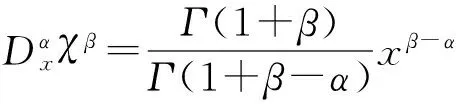
(8)
修正的Jumarie Riemann-Liouville分数阶导数具有Riemann-Liouville分数阶导数和Caputo分数阶导数二者的优点,并成功应用于分数阶拉普拉斯问题[21]、概率演算[22]、多变量的分数阶变分法[23]、分数阶变分迭代方法[24]和自然边界条件的分数阶变分法[25]等问题中。
2G′/G展开法概述
对于给定1+1维的非线性偏微分方程
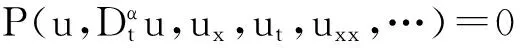
(9)
其中P是u及u关于x、t的各阶偏导数的多项式。该方法具体步骤如下:
步骤1文献[26]提到一个复杂分数阶变换可将分数阶偏微分方程转化为常微分方程。
复杂分数阶变换[26]为
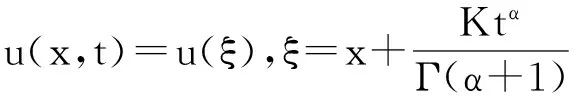
(10)
其中ξ为行波变量,K为任意非零常数。
将(10)式代入(9)式可得如下常微分方程
Q(u′,u″,u‴,…)=0。
(11)
步骤2设常微分方程(11)的解可表示为关于(G′/G)的多项式
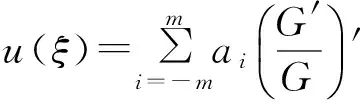
(12)
其中ai为待定常数且G=G(ξ)满足二阶线性常微分方程
G″(ξ)+λG′(ξ)+μG(ξ)=0。
(13)
步骤3(12)式中正整数m是由(11)式中线性最高阶导数项和非线性项,通过齐次平衡原理[27]确定。此处,假设u(ξ)的阶数为Deg[u(ξ)]=m,则其他表达式的阶数为
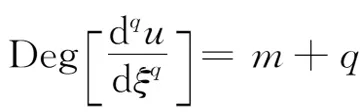
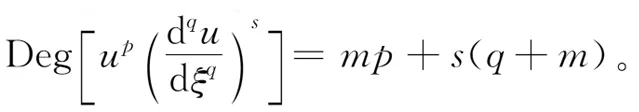
(14)
由此即可确定(12)式中m的值。
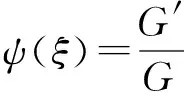
ψ′=-μ-λψ-ψ2。
(15)
因而,常微分方程(11)的解为
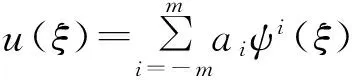
(16)
步骤5将(16)式代入(11)式,运用ψ(ξ)所满足的一阶常微分方程(15)来消除所有导数项,然后合并ψ(ξ)的相同幂次项,并令ψ(ξ)的各次幂的系数为零, 得到一个关于常量ai、K、λ、μ的非线性代数方程组。
步骤6求解上述代数方程组,将所得结果代入(16)式,并利用(13)式在不同情况下的通解,即可获得(9)式的多个不同类型的精确解。
3广义时间分数阶HS-KdV系统的精确解
对系统(1)引入复杂分数阶变换[26]
(17)
将(17)式代入系统(1),并结合上述修正的Jumarie Riemann-Liouville分数阶导数,系统(1)可转化为如下的常微分方程组
(18)
由于方程组(18)的精确解满足(16)式,则设解为
(19)
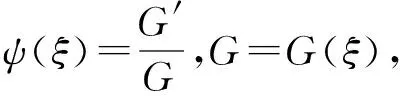
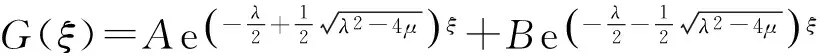
(20)
A、B为积分常数。故得
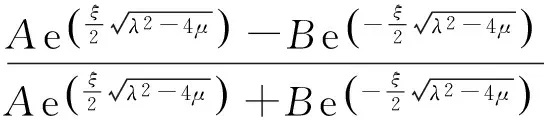
(21)
该解可表示为如下双曲函数形式
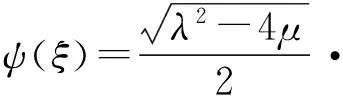
(22)
其中P=A-B,Q=A+B。
对方程组(18)应用齐次平衡原理[27]得,m=n=2,q为任意常数,此处取q=2。则系统(1)的解形式为
(23)
将(23)式分别代入常微分方程组(18)并利用(15)式化简可得关于ψ(ξ)的各阶幂次项,合并ψ(ξ)相同的幂次项,令ψ(ξ)的各次幂项的系数为零, 得到一个非线性代数方程组。使用符号计算系统Maple求解非线性代数方程组,可获得14组解。限于篇幅,本文仅列出耦合的广义时间分数阶Hirota-Satsuma-KdV方程的部分有物理意义的精确解。
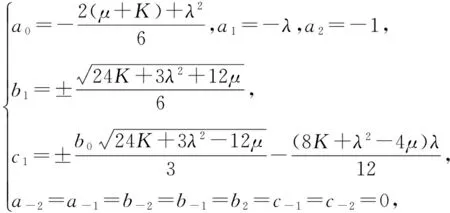
(24)
其中K、λ、μ为任意非零常数。将(24)式代入(23)式得
(25)
将(22)式代入(25)式,可在不同的参数约束条件下,获得系统(1)不同形式的精确解:
情形1-1当λ2-4μ<0,可得三角函数解
(26)
其中行波变量
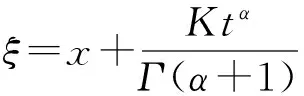
(27)
(28)
情形1-2当λ2-4μ>0,可得双曲函数解
(29)
其中,行波变量ξ以及S、H同(27)和(28)式。
对于情形1-2,考虑两种特殊情况,便可获得其如下形式的孤立波解。
情形1-2-1当A=B,即P=0,Q≠0,孤立波解为
(30)
情形1-2-2当A=-B,即P≠0,Q=0,孤立波解为
(31)

图1时间分数阶HS-KdV系统精确解(30)的三维图
(34)

情形2-2当λ2-4μ>0时,可得双曲函数解
(35)

对于情形2-2,考虑两种特殊情况,便可获得其如下形式的孤立波解。
情形2-2-1当A=B,即P=0,Q≠0,孤立波解为
(36)
情形2-2-2当A=-B,即P≠0,Q=0,孤立波解为
(37)
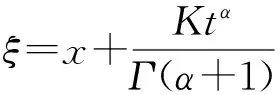

图2时间分数阶HS-KdV系统精确解(36)的三维图
(40)
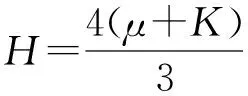
情形3-2当μ<0,可得双曲函数解
(41)
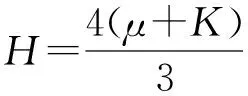
对于情形3-2,考虑两种特殊情况,便可获得其如下形式的孤立波解。
情形3-2-1当A=B,即P=0,Q≠0,孤立波解为
(42)
情形3-2-2当A=-B,即P≠0,Q=0,孤立波解为
(43)
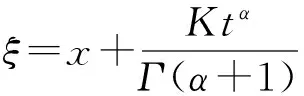
图3时间分数阶HS-KdVf(42)的三维图
(46)
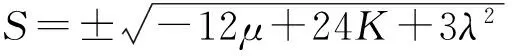
情形4-2当λ2-4μ>0,可得双曲函数解
(47)
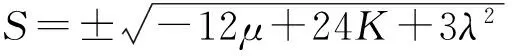
对于情形4-2,考虑两种特殊情况,便可获得其如下形式的孤立波解。
情形4-2-1当A=B,即P=0,Q≠0,孤立波解为
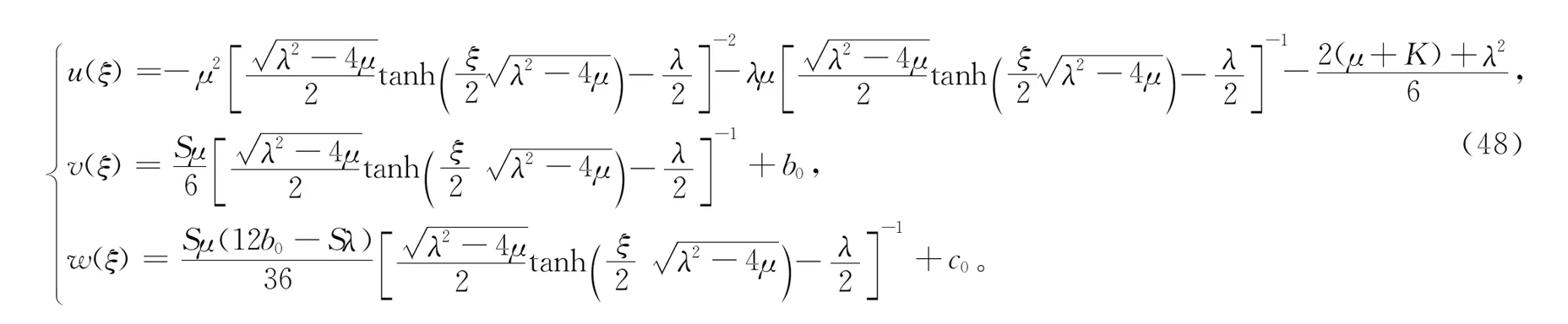
(48)
情形4-2-2当A=-B,即P≠0,Q=0,孤立波解为
(49)

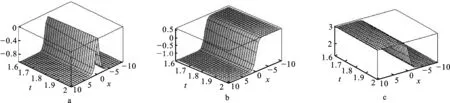
图4时间分数阶HS-KdV系统精确解(48)的三维图
(52)
4结语
本文利用复杂分数阶变量变换和修正的Jumarie Riemann-Liouville分数导数,并结合齐次平衡原理,通过(G′/G)展开法来求解广义时间分数阶Hirota-Satsuma耦合KdV系统的精确解,获得了该系统的含有多参数的新的双曲函数和三角函数形式精确解,且当双曲函数解取特殊值时即可获得其孤波解,从而丰富了广义时间分数阶Hirota-Satsuma耦合KdV系统的解系。限于篇幅,本文仅列出部分解。从求解过程及求得的精确解易知用此方法来求解这类非线性问题更直接、简洁和高效。但对于其他类问题能否适用还需进一步的研究。
参考文献:
[1] 郭柏灵. 分数阶偏微分方程及其数值解[M]. 北京:科学出版社,2011:2-30.
[2] 王在华. 分数阶微积分:描述记忆特性与中间过程的数学工具[J]. 科学中国人,2011(3):78-80.
[3] 邓伟华. 分数阶微分方程的理论分析与数值计算[D]. 上海:上海大学理学院,2007.
[4] 晏祥玉,周激流. 分数阶微积分在医学图像处理的应用[J]. 成都信息工程学院学报,2008,23(1):38-41.
[5] 宋建国,刘垒,李辉,等. 分数阶导数在地震奇异性分析中的应用[J]. 石油物探, 2009,48(1):90-93.
[6] 王少伟. 分数阶微积分理论在粘弹性流体力学及量子力学中的某些应用[D]. 济南:山东大学理学院,2007.
[7] 姚奎. 分形函数与分数阶微积分构造性方法的应用[D]. 杭州:浙江大学数学科学学院,2003.
[8] 王振滨,曹广益,曾庆山,等. 分数阶PID控制器及其数字实现[J]. 上海交通大学学报,2004,38(4):29-32.
[9] 袁晓,张红雨,虞厥邦. 分数导数与数字微分器设计[J]. 电子学报,2004, 32(10):75-82.
[10] PODLUBNY. Fractional differential equations[M]. New York:Academic Press,1999.
[11] 李娴娟. 分数阶偏微分方程的理论和数值研究[D]. 厦门:厦门大学数学科学学院,2009.
[12] 林玉闽. 时间分数阶偏微分方程的解及其应用[D]. 厦门:厦门大学数学科学学院,2008.
[13] WANG M L,LI X Z,ZHANG J L. The expansion method and traveling wave solutions of nonlinear evolution equations in mathematical physics[J]. Physics Letters A, 2008,21(4):417-423.
[14] 胡桐春,钱德亮,李常品. 分数阶微分方程的比较定理[J]. 应用数学与计算数学学报,2009(1):99-105.
[15] 林孔容. 关于分数阶导数的几种不同定义的分析与比较[J]. 闽江学院学报,2003,24(5):8-11.
[16] JUMARIE G. Modified riemann-liouville derivative an fractional taylor series of nondifferentiable functions further results[J]. Journal of Computational and Applied Mathmatics,2006,51(9/10):1367-1376.
[17] ATANGANA A,SECER A. A note on fractional order derivatives and table of fractional derivatives of some special functions[J]. Abstract and Applied Analysis,2013,2013:279681.
[18] LIU W J,CHEN K W. The functional variable method for finding exact solutions of some nonlinear time-fractional differential equations[J]. Indian Academy of Sciences,2013,81(3):377-384.
[19] GANJI Z Z,GANJI D D,ROSTAMIYAN Y. Solitary wave solutions for a time-fraction Hirota-Satsuma coupled KdV equation by an technique[J]. Applied Mathematical Modelling,2009,33:3107-3113.
[20] MERDAN M,GÖKDOAN A. Solution of time-fraction generalized Hirota-Satsuma coupled KdV equation by generalized differential transformation method[J]. Methods for Heat &Fluid Flow,2013,23(5):927-940.
[21] JUMARIE G. Table of some basic fractional calculus formulae derived from a modified Riemann-Liouville derivative for non-differentiable functions[J]. Applied Mathematics Letters,2009,22(3): 378-385 .
[22] JUMARIE G. New stochastic fractional models for Malthusian growth, the Poissonian birth process and optimal management of populations[J]. Mathematical and Computer Modelling, 2006, 44(3/4): 231-254.
[23] ALMEIDA R,MALINOWSKA A B,TORRES D F M. A fractional calculus of variations for multiple integrals with application to vibrating string[J]. Journal of Mathematical Physics,2010,51:033503.
[24] WU G C, LEE E W M. Fractional variational iteration method and its application[J]. Physics Letter A, 2010, 374: 2506-2509.
[25] WU G C. A fractional characteristic method for solving fractional partial differential equations[J]. Applied Mathematics Letters,2011,24(1):1046-1050.
[26] LI Z B,HE J H. Application of the fractional complex transform to fractional differential equations[J]. Science Letters Mathematics Physics and Mechanics,2011,2(3):121-126.
[27] 王明亮,李志斌,周宇斌. 齐次平衡原则及其应用[J].兰州大学学报,1999(3):8-16.
[28] 庞晶,靳玲花,应孝梅. 利用(G′/G)-展开法求解广义变系数Burgers方程[J]. 量子电子学报,2011,28(6):674-681.
[29] 郭冠平,周国中,何宝钢.(G′/G)-展开法对非线性耦Klein-Gordon方程组的精确解[J]. 浙江师范大学学报(自然科学版),2010,33(3):286-290.
[30] 尹君毅. 扩展的(G′/G)展开法和Zakharov方程组的新精确解[J]. 物理学报,2013, 62(20): 200202.
〔责任编辑宋轶文〕
New exact solutions of the coupled time-fractional generalized Hirota-Satsuma and KdV system
WANG Miaomiao, YAO Ruoxia*
(School of Computer Science, Shaanxi Normal University,Xi′an 710119, Shaanxi, China)
Key words:fractional complex transformation; time-fractional Hirota-Satsuma-KdV system;G′/G-expansion method; Jumarie′s Riemann-Liouville derivative; exact solution
Abstract:By means of the Jumarie′s modified Riemann-Liouville fractional derivative and the fractional complex transformation, using the solution of a second order ordinary differential equation and based theG′/G-expansion method, the coupled nonlinear time-fractional Hirota-Satsuma-KdV system is studied. Several hyperbolic function and trigonometric function exact solutions of this system are obtained, which enrich the exact solution family.
文章编号:1672-4291(2016)03-0022-10
doi:10.15983/j.cnki.jsnu.2016.03.135
收稿日期:2014-12-23
基金项目:国家自然科学基金(11471004,1172342);中央高校基本科研业务费专项资金(GK201302026)
*通信作者:姚若侠,女,教授,博士生导师。E-mail:rxyao2@hotmail.com
中图分类号:O175.6
文献标志码:A

