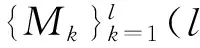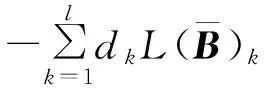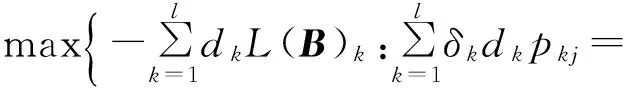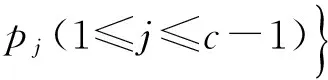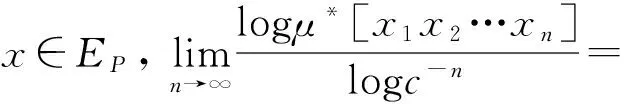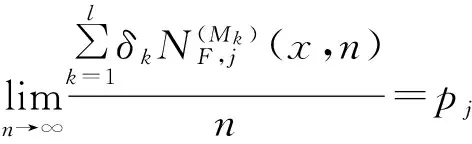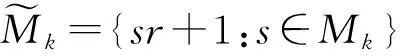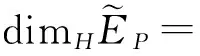加权Besicovitch-Eggleston集的Hausdorff维数
董秀英, 刘卫斌
(武汉大学 数学与统计学院, 湖北 武汉 430072)
加权Besicovitch-Eggleston集的Hausdorff维数
董秀英, 刘卫斌*
(武汉大学 数学与统计学院, 湖北 武汉 430072)
摘要:研究符号空间上的一类特殊的加权Besicovitch-Eggleston集,即具有右可重排性质的元胞自动机作用下的加权Besicovitch-Eggleston型集。通过构造一个概率测度及应用Billingsley定理,得到此类集合的Hausdorff维数dimHEF,P。关键词: 符号空间; 加权Besicovitch-Eggleston集; 元胞自动机; Hausdorff维数
MR subject classification: 28A78

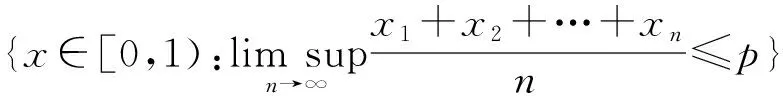
并在1934年证明了它的Hausdorff维数
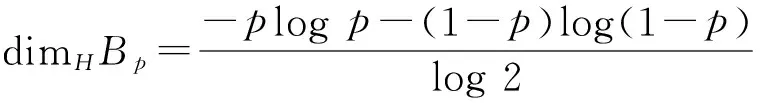




(i=0,1,…,c-1)},
Eggleston证明了

集合Eq亦被称作Besicovitch-Eggleston集。
文献[3]研究{0,1}N符号空间上的加权Besicovitch集,并计算其Hausdorff维数,本文主要将其向c个字符的符号空间作推广,研究符号空间Ω={0,1,…,c-1}N上在右可重排的元胞自动机作用下的加权Besicovitch-Eggleston集,并给出其Hausdorff维数的计算公式。
为方便起见,介绍文中用到的记号:


(本文假设每个dk均存在)。
(2) 令A={0,1,…,c-1},Ω=AN={0,1,…,c-1}N是c个字符的符号空间,∀x=x1x2…∈Ω,∀n∈N,Nk(n)表示集合{Mk∩[1,n]}的势,即


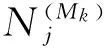
(0≤j≤c-1)。
(1)

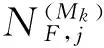
(2)
(4)ψkj(x,n)表示符号j在x的Mk∩[1,n]项中出现的频率,即
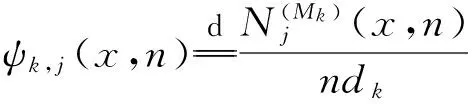
(5)B=(pij)l×(c-1)是一个矩阵且满足pij≥0


(1≤k≤l,规定0log 0=0)。



(3)
我们将确定它的Hausdorff维数。
从元胞自动机的观点看,易知(1)式等价于如下形式:
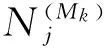
其中σ是Ω→Ω上的移位映射,σ(x)=(xi+1)i∈N,∀x=(xi)i∈N。注意到映射σ是具有右可重排性质的元胞自动机,因此(1)式只是(2)式的特殊形式。
1预备知识
有关Hausdorff测度及Hausdorff维数的相关的定义和性质参见文献[5],下面给出文中用到的性质、定义和引理:
定理1设D⊂Rn,若f:D→Rm为双利普希茨变换,即
c1|x-y|≤|f(x)-f(y)|≤
c2|x-y|(x、y∈D),
其中0 pij≥0(i=1,2,…,l;j=0,1,…,c-1), 令 则 详细证明见文献[4]中定理3。 有关符号空间的一些定义如下: d(x,y)=c-inf(i:xi≠yi}。 定义1设X是一个紧空间,T:X→X是连续映射,则称(X,T)是动力系统。对于两个动力系统(X,T)和(Y,G),如果存在一个连续的双射φ:X→Y满足φ∘T=G∘φ,则称(X,T)和(Y,G)共轭。 下面对元胞自动机作简单的介绍,关于元胞自动机的知识可参见文献[8-10]。 定义2如果存在半径r∈N和局部规则f:Ar+1→A使得 F(x)i=f(xi,…,xi+r), ∀x∈Ω。 称映射F:Ω→Ω为元胞自动机。 例1Ω上的移位映射 σ(x)=(x2x3x4…),其中x=(x1x2x3…)∈Ω,以及{0,1}N上的求和映射 F(x)i=xi+xi+1, (mod 2)=:(xi+xi+1)2, ∀i≥1其中x=(x1x2x3…)∈{0,1}N都是半径为1的元胞自动机。 Hedlund[10]给出了元胞自动机的一个判别法则。 定理2[10]映射F:Ω→Ω为元胞自动机当且仅当映射F在空间Ω上是连续的,并且与移位映射σ是可交换的,即F∘σ=σ∘F。 下面介绍一类重要的元胞自动机——具有右可重排性质的元胞自动机。 定义3如果∀u∈Ar和∀b∈A,都存在唯一的a∈A满足f(ua)=b,则称(Ω,F)具有右可重排性。 例2(1)Ω上的移位映射σ的局部规则是f(xi,xi+1)=xi+1,从而具有右可重排性。 (2) {0,1}N上的求和映射F具有右可重排性。 性质1具有右可重排性的元胞自动机(Ω,F)是满射,但不是单射。 引理2设F是Ω上半径r≥1的自动机,且具有右可重排性,那么(Ω,F)共轭于(Ω,σr)。 证明定义映射φ:Ω→Ω为 φ(x)=x1x2…xrF(x)1F(x)2…F(x)r… Fn(x)1…Fn(x)r…,x=x1x2…∈Ω。可以证明φ是一个连续的双射,且是等距映射,并且满足φ∘F=σr∘φ,由共轭的定义即得引理成立。 2主要结果及其证明 我们先证明当元胞自动机F取为移位映射σ时,集合EF,P的Hausdorff维数,即下面定理中集合EP的Hausdorff维数。 定理3令l是一个有限的正整数,P=(p1,p2,…,pc-1),0≤pj≤1(1≤j≤c-1),集合 则 证明(1) 因为 由Lagrange乘数法知 (k=1,2,…,l;j=1,2,…,c-1), (4) (j=1,2,…,c-1), (5) 由(4)、(5)式得 则 (j=1,2…,c-1),μ*a.e.x∈Ω。 因此, 此即证明了μ*(EP)=1。由Billingsley定理[4]即知 注1当l=1时,EP即是经典的Besicovitch-Eggleston集,定理3的结论与Eggleston定理[2]是一致的。 下面我们将对一般的具有右可重排性质的元胞自动机F确定集合EF,P的Hausdorff维数。 定理4设F是Ω上半径为r≥1的元胞自动机,并且具有右可重排性,对于给定的概率向量P=(p1,…,pc-1),其中0≤pj≤1(1≤j≤c-1)且 集合 则集合EF,P的Hausdorff维数为 证明由引理2知,存在等距映射φ:Ω→Ω定义为 φ(x)=x1x2…xrF(x)1F(x)2…F(x)r… Fn(x)1…Fn(x)r…,x=x1x2…∈Ω, 并且满足φ∘F=σr∘φ,则有如下等价关系: (1≤j≤c-1)⟺ pj(1≤j≤c-1)⟺ pj(1≤j≤c-1)⟺ 令 3结论 在右可重排元胞自动机作用下的Besicovitch-Eggleston型集的Hausdorff维数与元胞自动机的半径相关,与元胞自动机的具体形式无关。 参考文献: [1]BESICOVITCHA.Onthesumofdigitsofrealnumbersrepresentedinthedyadicsystem[J].MathematischeAnnalen,1934,110(1):321-330. [2]EGGLESTONHG.Thefractaldimensionofasetdefinedbydecimalproperties[J].QuarterlyJournalofMathematics(OxfordSeries),1949,20(2):31-36. [3]XIEYQ,WENZX,YUM.DimensionsofWeightedBesicovitchsets[J].ActaMathematicaSinicaEnglishSeries,2010,26(4):711-716. [4]XIEYQ,WENZX.DimensionsofmodifiedBesicovitch-Egglestonset[J].ScienceinChina:SeriesAMathematics,2006,49(2):245-254. [5] 文志英.分形几何的数学基础[M].上海:上海科技教育出版社,2000:43-49. [6]SHERESHEVSKYMA.Ergodicpropertiesofcertainsurjectivecellularautomata[J].MonatsheftefürMathematik,1992,114(3/4):035-316. [7]YUM,WENZX,XIONGY.TheHausdorffDimensionofweightedBesicovitchset[J].JournalofMathematics,2007,27(2):141-144. [8]LINDD,MARCUSB.Anintroductiontosymbolicdynamicsandcoding[M].Cambridge:CambridgeUniversityPress,1995. [9]KURKAP.Topologicalandsymbolicdynamics[M].Paris:CoursSpécialisés-CollectionSMF,2003. [10]HEDLUNDGA.Endomorphismsandautomorphismsoftheshiftdynamicalsystem[J].TheoryofComputingSystems,1969,3:320-375. 〔责任编辑宋轶文〕 Hausdorff dimensions of weighted Besicovitch-Eggleston sets DONG Xiuying, LIU Weibin* (School of Mathematics and Statistics, WuHan University, Wuhan 430072, Hubei, China) Keywords:symbolic space; weighted Besicovitch-Eggleston sets; celluar automata; Hausdorff dimension Abstract:A class of weighted Besicovitch-Eggleston sets by the action of cellular automata which is right permutive in symbolic space were studied.By constructing a probability measure and applying Billingsley′s theorem,we obtain explicit formulas for their Hausdorff dimensions dimHEF,P. 文章编号:1672-4291(2016)03-0011-06 doi:10.15983/j.cnki.jsnu.2016.03.133 收稿日期:2015-07-09 基金项目:国家自然科学基金(11171128); 中央高校基本科研业务费专项资金(2012201020204) *通信作者:刘卫斌,男,讲师,博士。E-mail:weibinliu@whu.edu.cn 中图分类号:O174.12 文献标志码:A