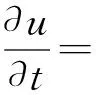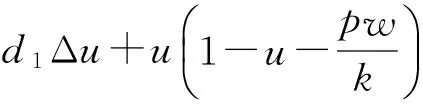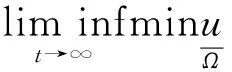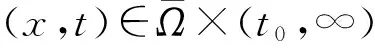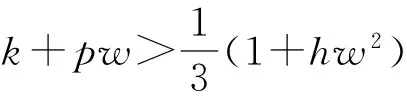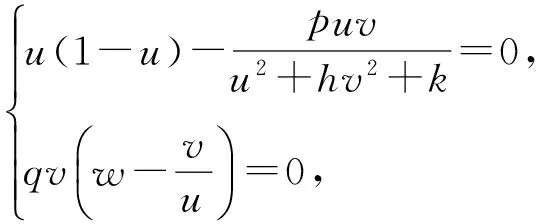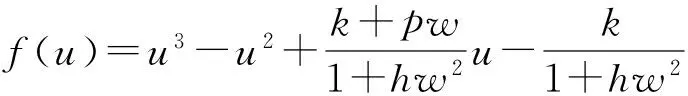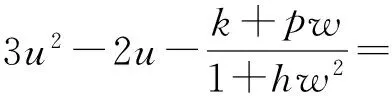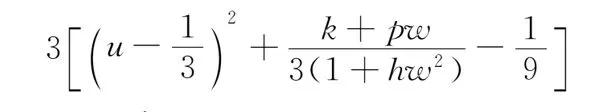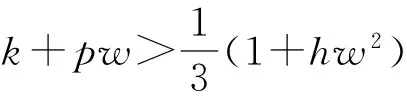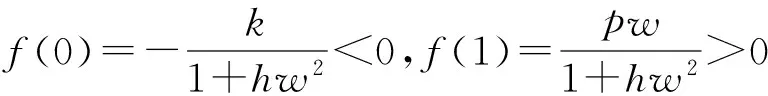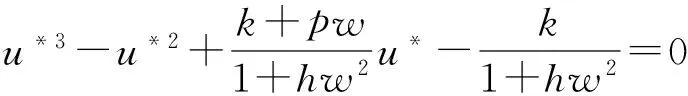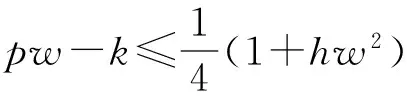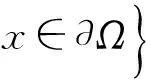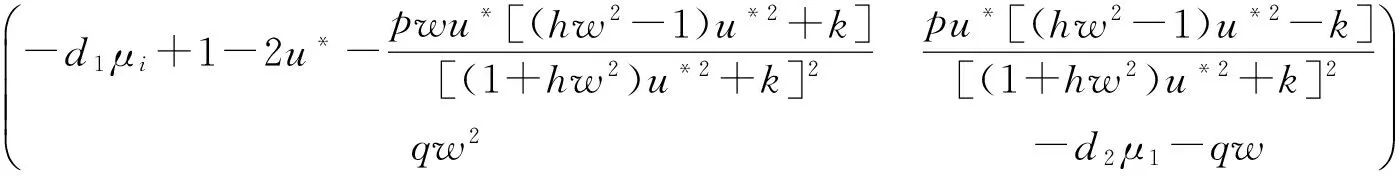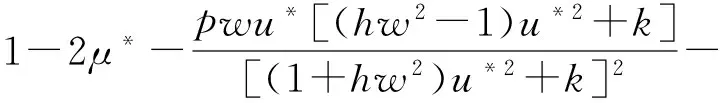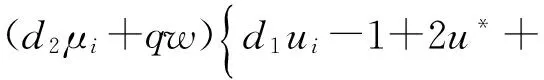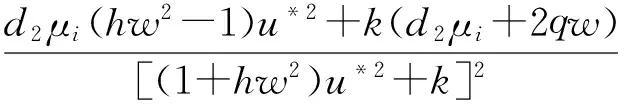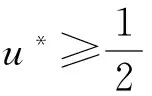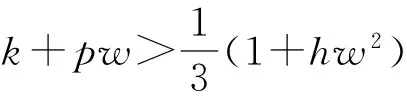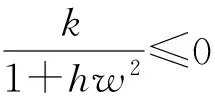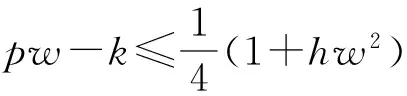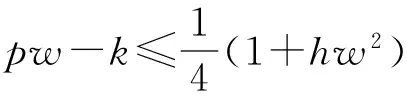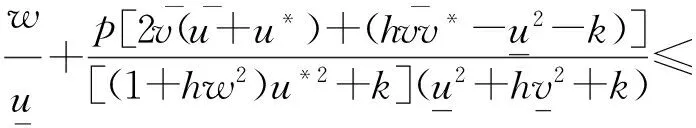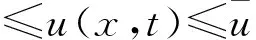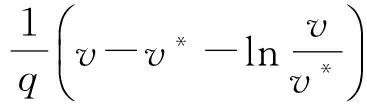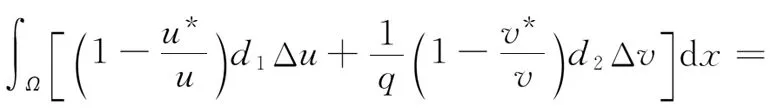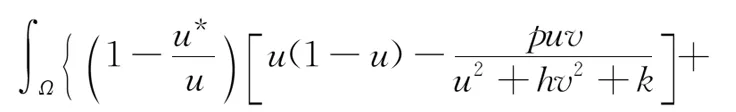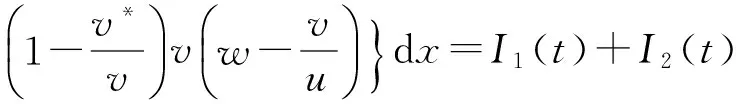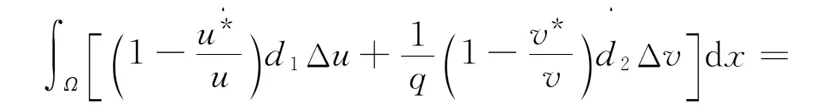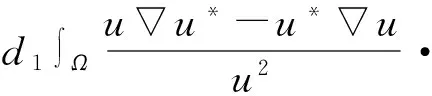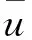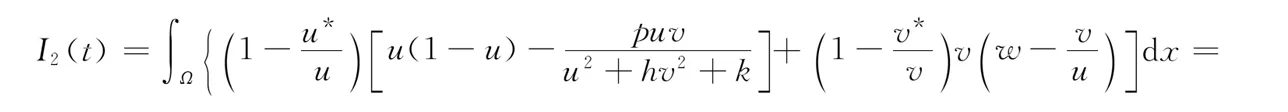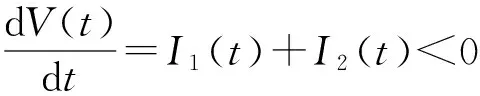一类扩散的食饵-捕食模型
高杏杏, 胡志兴, 廖福成
(北京科技大学 数理学院, 北京100083)
一类扩散的食饵-捕食模型
高杏杏, 胡志兴*, 廖福成
(北京科技大学 数理学院, 北京100083)
摘要:研究一类扩散并具有比率依赖功能反应函数的Leslie-Gower模型。 运用比较原理得到了系统的持久性。应用谱理论, 探讨正平衡点的局部渐近稳定性。利用李雅普诺夫函数研究了正平衡点的全局稳定性。关键词: Leslie-Gower模型; 扩散; 比率依赖
MR subject classification: 35K57
捕食关系一直是种群动力学中最基本而广泛的一个方面, 而经典的Leslie-Gower模型的特点在于捕食者满足Logistic增长规律, 其中捕食者的环境容纳量与食饵数量成正比。 对于改进的Leslie-Gower模型, 已有许多学者做过改进, 也取得不少成果[1-7]。
由于在捕食关系中, 空间对种群的各项形态特征有很大的影响, 因此, 在模型中考虑扩散很有必要,文献[1-3]在模型中均加入了扩散的影响。此外, 也有更多的研究表明, 捕食者在寻找食物时, 食饵和捕食者自身的种群密度都会对其造成影响, 即具有比率依赖的功能性反应函数可以更好地反映实际情况, 文献[4-6]在模型中均选择了具有比率依赖的功能反应函数。 文献[4]研究了具有比率依赖的Holling-Ⅲ功能性反应函数的Leslie-Gower模型
(1)
本文将(1)式的功能性反应函数进一步改进, 建立了新的模型。
1模型的建立
在模型(1)的基础上, 我们考虑将功能性反应函数变为具有比率依赖的Holling-Ⅳ型反应函数, 建立模型如下:
(2)
其中,u(x,t)、v(x,t)分别表示t时刻食饵与捕食者的种群密度; 正常数d1、d2分别为扩散系数;Δ为Laplace算子;Ω⊂Rn表示具有光滑边界∂Ω的有界开区域, 并满足齐次Neumann边界条件,即边界上没有种群迁移;n为∂Ω上的单位外法向量; 初始条件u0(x)、v0(x)均为非负连续函数;a、b、c、m、l、s、e均为正常数。
为了表示方便,作以下变换:
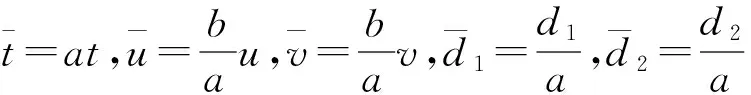
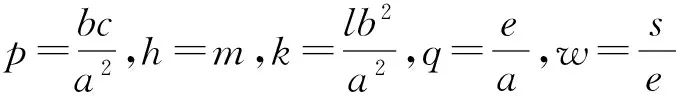
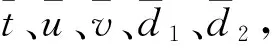
(3)
2系统的持久性
引理1[7]若z(x,t)满足以下方程组
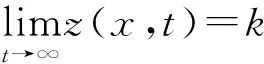
定理1系统(3)的解(u,v)满足以下两式:
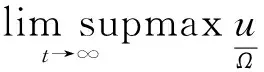
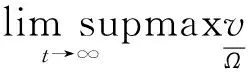
证明由系统(3)的第1式可得:
d1Δu+u(1-u),(x,t)∈Ω×[0,∞)。
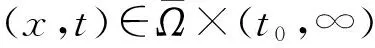
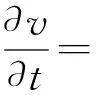
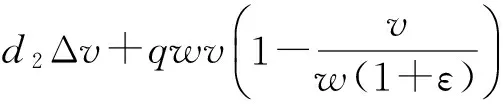
同理,由比较原则及ε的任意性可知,
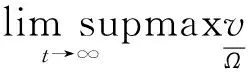
定理得证。
定义1[4]如果系统(3)的初始条件u0(x)、v0(x)非负且均不恒为0, 并存在正常数ε1、ε2,使得系统(3)的解(u(x,t),v(x,t)满足以下两式:
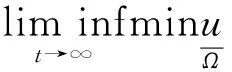
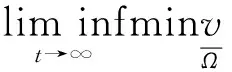
那么称系统(3)一致持久。
定理2如果pw 因此,当pw 3正平衡点的稳定性 3.1正平衡点的存在性 证明若系统存在唯一的正平衡点,则应满足 v*=wu*。 3.2正平衡点的局部稳定性 证明我们做出如下假设: (1) 满足齐次Neumann边界的条件下, 设0=μ0<μ1<μ2<…是Ω上-Δ的特征值。 (2)T(μ1)是相应于μ1的特征空间。i=0,1,2,…。 (3)Xij={kφij|k∈R2},其中{φij}是T(μi)的正交基,j=0,1,2,…;dim[T(μj)]。 将系统(3)在E*处线性化后可得 Zt=[DΔ+GZ(Z*)]Z 其中 Z=(u(x,t),v(x,t))T, D=diag(d1,d2)。 对于每个i≥1,Xi是算子DΔ+Gz(Z*)的不变子空间, 则λ是算子DΔ+GZ(Z*)在Xi上的特征值⟺λ是矩阵Mi=-μiD+GZ(Z*)的特征值, 其中 则det(λI-Mi)=λ2-λ·trMi+det Mi, 其中 (d1+d2)μ1-qw, (d2μi+qw)(d1μi-1+2u*)+pwu*· 3.3正平衡点的全局稳定性 定理5当满足如下条件(a)—(d)时,系统(3)正平衡点E*(u*,v*)全局稳定, 其中 (a)pw (b)w≤2, 证明令u(x,t),v(x,t)为系统(3)的一个正解, 考虑如下函数: V(t)=∫ΩM(u(x,t),v(x,t))dx。 则 首先,由格林公式及齐次Neumann边界条件, 可得 -d1∫Ωvdx= d1∫Ωvdx= 时,恒有I2(t)<0,则 因此,系统在E*处全局稳定。 4结论 本文研究了一类改进的Leslie-Gower模型, 其特点是考虑了扩散的影响并采用了具有比率依赖的功能性反应函数,更符合自然情况下种群捕食的实际情况。 首先, 分析了种群能够持续生存的条件; 其次, 研究了系统存在唯一正平衡点E*的条件; 最后,分别探讨了E*局部渐近稳定、全局稳定的情况。 研究表明,在一定的条件下, 捕食者与食饵能共存, 它们最终达到一定数量, 这将助于我们进一步研究自然界中种群的捕食关系。 参考文献: [1] TIAN Y L, WENG P X. Stability analysis of diffusive predator-prey model with modified Leslie-Gower and Holling-type Ⅲ schemes[J]. Applied Mathematics and Computation, 2011, 218: 3733-3745. [2] YANG W S. Global asymptotical stability and persistent property for a diffusive predator-prey system with modified Leslie-Gower functional response[J]. Nonlinear Analysis, 2013, 14: 1323-1330. [3] YIN H W, ZHOU J X, XIAO X Y, et al. Analysis of a diffusive Leslie-Gower predator-prey model with nonmonotonic functional response[J]. Chaos, Solitons & Fractals, 2014,65:51-61. [4] SHI H B, LI Y.Global asymptotic stability of a diffusive predator-prey model with ratio-dependent functional response[J]. Applied Mathematics and Computation, 2015, 250: 71-77. [5] WANG Q, ZHANG Y M, WANG Z J, et al. Existence and attractivity of a periodic solution for a ratio-dependent Leslie system with feedback controls[J]. Nonlinear Analysis, 2011, 12: 24-33. [6] 查淑玲, 李艳玲. 一类具有比率依赖反应函数的捕食模型的整体分歧[J].陕西师范大学学报(自然科学版),2009,37(4):17-20. [7] 叶其孝, 李正元, 王明新, 等.反应扩散方程引论[M]. 2版.北京: 科学出版社, 2011. 〔责任编辑宋轶文〕 A diffusive predator-prey model GAO Xingxing, HU Zhixing*, LIAO Fucheng (College of Mathematics and Physics, University of Science and Technology Beijing, Beijing 100083, China) Key words:Leslie-Gower model; diffusion; ratio-dependent Abstract:A diffusive Leslie-Gower model with ratio-dependent functional response is studied.The permanence of the system is obtained by using the comparison principle.Based on Spectrum Theory, locally asymptotic stability of the positive equilibrium is discussed.The Lyapunov function is used to analyze the Global stability of the positive equilibrium. 文章编号:1672-4291(2016)03-0017-05 doi:10.15983/j.cnki.jsnu.2016.03.134 收稿日期:2015-05-14 基金项目:国家自然科学基金(11471034,61174209); 北京科技大学冶金工程研究院基础研究基金(YJ2012-001) *通信作者:胡志兴,男,教授。E-mail:huzhixing@ustb.edu.cn 中图分类号:O175 文献标志码:A