炸药震源激发近区介质的粘滞性分析

陈　杰，翟开静，秦　龙

(西南石油大学　地球科学与技术学院，成都　610500)



炸药震源激发近区介质的粘滞性分析

陈杰，翟开静，秦龙

(西南石油大学地球科学与技术学院，成都610500)

摘要：在我国陆地石油勘探中，炸药震源依然是地震勘探的主要震源,炸药爆炸后会产生不同的分区，包括空腔、过渡区和弹性区。如今对地震子波产生机理的分析主要是基于等效球腔模型，忽略了过渡区对波传播特征的影响。为了定性描述过渡区的岩石破碎和永久形变对地震波传播特征的影响，将模型简化为粘弹性介质。这里在Kelvin粘弹性模型基础上推导了地震波传播的相速度和品质因子Q的表达式，并对Kelvin粘弹性模型进行数值模拟，从振幅、相位及频率的角度，分析品质因子Q对地震波传播特征的影响。结果表明，地震波在粘弹性介质中传播时，振幅、频率及相位特征是有变化的，这为研究炸药震源激发产生地震子波的机理提供了理论方向，为实际介质中的地震记录特征分析提供了理论基础，同时对补偿粘滞性因素的影响、提高地震资料的品质具有重要的实际意义。

关键词：炸药震源；Kelvin粘弹性模型；品质因子；数值模拟；波动方程

0引言

炸药作为陆上地震勘探的主要震源，是将炸药的化学能转换成机械能传向周围介质。为了知道炸药爆炸环境对地震子波的影响，国内、外学者建立了许多数学物理模型来模拟初始脉冲的激发过程。国外学者Sharp[1]和Blake基于无限大均匀弹性介质的假定，提出了“等效球腔半径”的概念，建立了许多函数来描述炸药爆炸后在球腔上形成的压力，并推导出了波动方程的位移位解；国内学者肖建华等[3]基于退行边界条件，得到了地震子波的解析解，定性讨论了子波随最大弹塑性半径不同而变化的情况；孙成禹等[4]得出了在等效球腔模型下腔壁压力随时间的变化关系，并推导出了在弹性介质中空腔震源产生地震子波位移的解析解；成景旺等[5]通过计算得到了均匀弹性介质中球腔震源作用下的位移公式，并分析了影响球腔震源子波的各个因素；於文辉[6]讨论了应力波的蜕变点落在塑性区中波的传播情况，并得出了塑性区波的传播与弹性区波的传播满足的线弹性波动方程是一致的，只是波的传播速度受塑性区塑性因子影响而比弹性区波的传播速度小的结论。

在对炸药震源爆炸模型的众多假设中，等效球腔半径模型被大量学者引用。这种模型避开了对破碎区和塑性区内地震波传播特征的讨论，它假设点震源爆炸后产生的球形空腔半径相对于炸药包半径是足够大的，以至于爆炸冲击波未能使空腔壁发生塑性变形，而是保持弹性变形。而实际炸药爆炸时在其周围介质中常会形成多个区(图1)：破碎区和塑性区(统称过渡区)，过渡区会影响波的动力学[7]和运动学特征。Farrokh Jalinoos等[8]从炸药爆炸后介质的受力和变形入手，将爆腔周围介质分为弹性区和粘性区(图2)，建立了弹性区和粘性区的应力应变方程组，进而分析了地震波的产生和传播情况。Victoria M.Yarushina等[9]根据波的加载和卸载过程，从弹塑性力学角度分析了波在弹塑性区的传播特征。

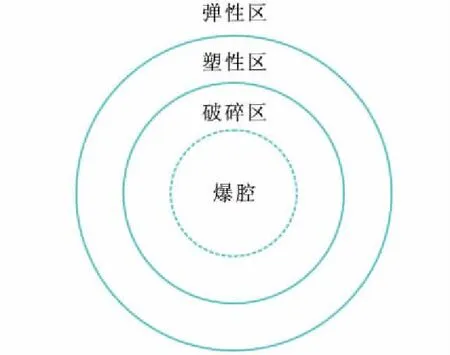
图1　爆炸分区Fig.1　The explosion partition

图2　爆炸分区简化模型Fig.2　The simplified model of explosion partition

作者根据Kelvin粘弹性模型理论，通过交错网格有限差分[10]数值模拟得到正演记录，从记录上提取地震道，然后分析品质因子Q对地震波振幅、频率及相位的影响，以定性说明过渡区中地震波传播的特征。

1Kelvin粘弹性介质理论

Kelvin粘弹性介质(又叫斯托克斯(Stocks)粘弹性体或佛格特(Voigt)粘弹性体[11])如图3所示，这种介质模型是用一个表示弹性的弹簧器和一个表示粘性的阻尼器并联来描述固体的非完全弹性特征。

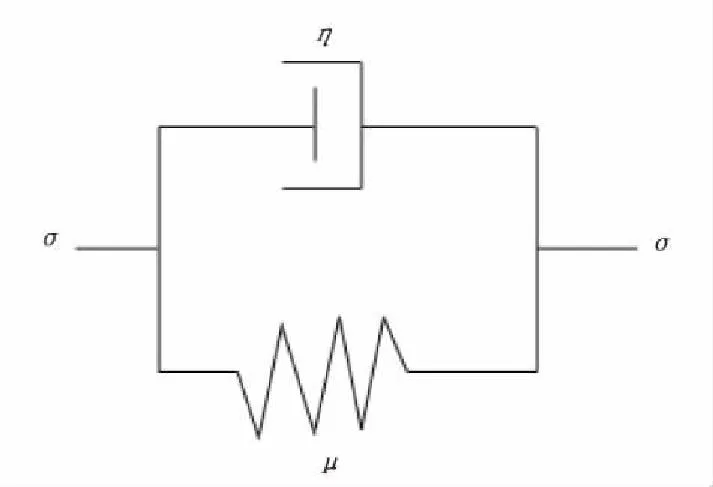
图3　开尔芬模型Fig.3　Kelvin model

为了与均匀各向同性的弹性介质模型做比较分析，给出了二维弹性波方程的表达式。在均匀各向同性介质中，矢量形式的弹性波动方程如式(1)所示。

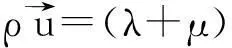
(1)

根据粘弹性理论，应变的大小不仅与载荷有关，还与形变历史有关。因此，根据Kelvin粘弹性介质模型，粘弹性波动方程的矢量表达式见式(2)。

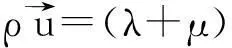
(2)

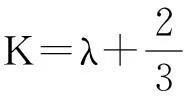
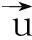
(3)

(4)

在各向均匀介质中，式(3)和式(4)的频率域形式见式(5)和式(6)。

(5)

(6)

(7)

引入衰减系数ηp，其表达式为式(8)，它表示波在粘弹性介质里传播时的衰减程度，值越大，衰减越严重。

(8)

定义品质因子为如式(9)所示。

(9)

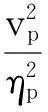
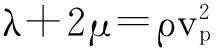
(10)

当Qp为常数时，式(10)在时间域的形式可以表示为式(11)。

(11)

(12)

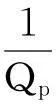
(13)

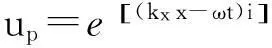
(14)

由式(13)可以看出，当Qp→∞时，式(14)可以看出，其实部描述了波振幅的衰减特性，由式(9)分析知道，波的高频成分较低频成分衰减快，而波的振幅是呈指数衰减，因此随着传播时间或距离的增加，波的能量分布频带朝着低频方向移动。同样，随着品质因子 的减小，波的能量分布频带也向着低频方向移动。

2模型试算

2.1两层均匀介质

为了在计算机中模拟地震波的传播，需要将微分方程离散化。目前用得最广泛的数值离散方法有虚谱法、有限元法和有限差分法[13]。这里采用有限差分法进行粘弹性波动方程的数值模拟。

用Kelvin粘弹性介质中进行正演模拟时，给定的参数需要满足稳定性条件：

(15)

当 Q→∞时，

(16)

此时，与弹性状态下的稳定条件一致。

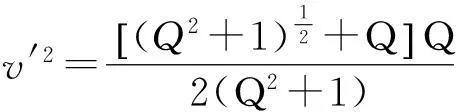
根据Kelvin模型稳定性条件(式15)，建立如图4所示的地质模型，模型大小为600 m×600 m，第一层速度为2 000 m/s，第二层速度为3 000 m/s。震源子波主频为50 Hz，时间步长为0.5 ms，纵向和横向网格大小均为3 m，配置纵波震源模拟炸药震源，震源位置位于模型网格(100，0)处，吸收边界采用PML边界条件。分析中横波的品质因子Qp=80。

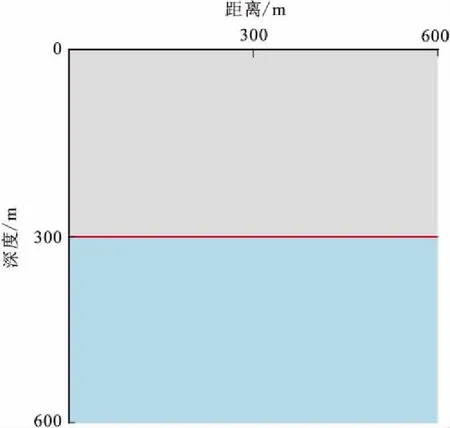
图4　地质模型Fig.4　The geological model

图5、图6为分别采用弹性波动方程和粘弹性波动方程正演得到的单炮记录。从图5、图6可以看出，粘弹性波的反射波同相轴能量比弹性波的反射波同相轴弱，波形和相位也发生畸变。图7为第40道弹性波记录和粘弹性波记录的对比。从图7可以看出，弹性波反射记录的振幅比粘弹性波反射记录的振幅大。图8为第40道弹性波记录和粘弹性波记录反射PP波的振幅谱。图8中，弹性波的主频在50 Hz，即震源子波的主频，而粘弹性波记录的主频向坐标左边移动，即变小，且振幅也减小。图9为不同的品质因子与PP反射波频谱的关系曲线，反射波主频向低频方向移动，频宽变窄；高频成分比低频成分衰减更快；品质因子越大(粘滞系数越小)，振幅越大，能量衰减越小，当品质因子增大到一定程度时，粘弹性波频谱曲线与弹性波频谱曲线基本重合，难以识别。

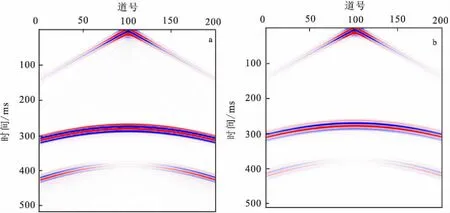
图5　垂直分量单炮记录Fig.5　Single shot simulated records of vertical component(a) 弹性波;(b) 粘弹性波(Qp=80)

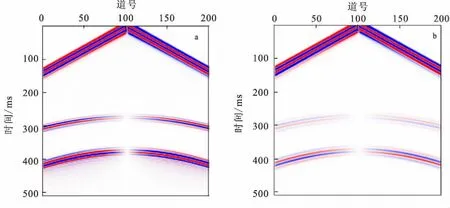
图6　水平分量单炮记录Fig.6　Single shot simulated records of horizontal component(a) 弹性波;(b) 粘弹性波(Qp=80)

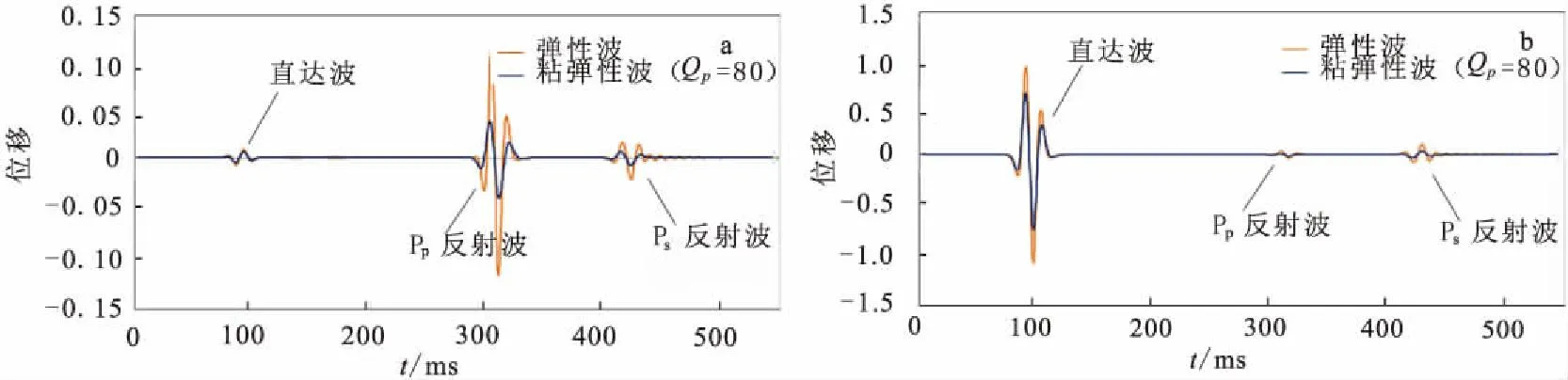
图7　第40道弹性波记录和粘弹性记录Fig.7　The forty trace records of elastic and viscoelasticity(a)垂直分量；(b)水平分量

2.2Marmousi复杂模型

采用复杂的Marmousi模型，使用弹性波动方程和粘弹性波动方程正演模拟得到单炮记录，从单炮记录上验证了粘弹性的对能量的衰减作用。Marmousi纵波速度模型如图10所示，模型横、纵向网格数为460×250，横、纵向网格步长均为6 m，时间步长为0.5 ms，密度为常数。采用纵波震源激发，子波为雷克子波，子波主频为50 Hz，在网格(230，0)处激发，其中粘弹性方程模拟时横波品质因子为常数Qs=120。边界吸收方式采用PML边界条件处理，差分精度为Ο(Δt2+Δx6)。

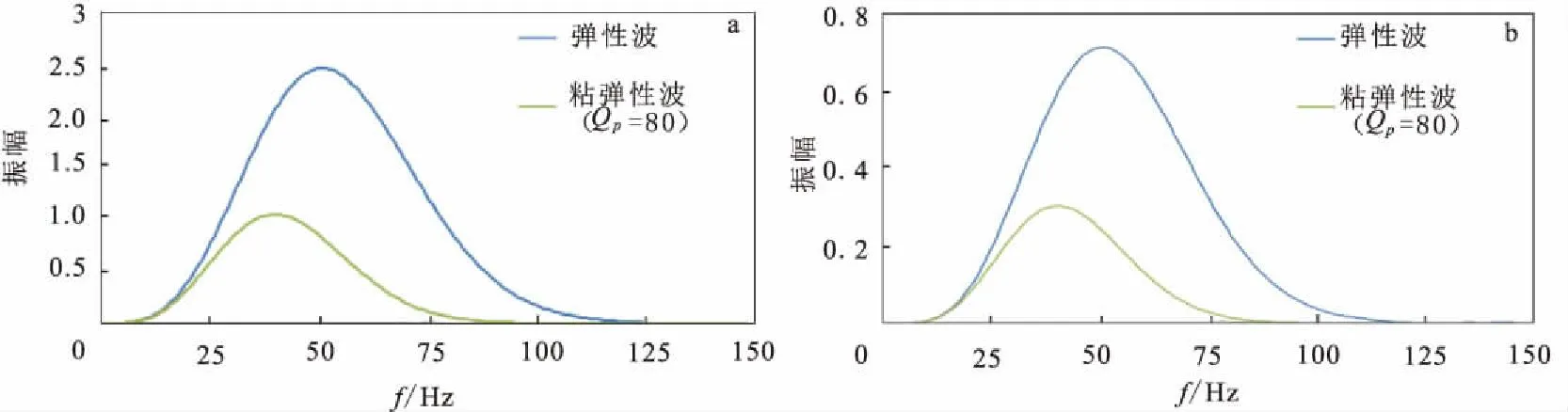
图8　第40道弹性波记录和粘弹性记录反射PP波振幅谱Fig.8　The forty trace amplitude spectrum of pp wave of elastic and viscoelasticity(a)垂直分量；(b)水平分量

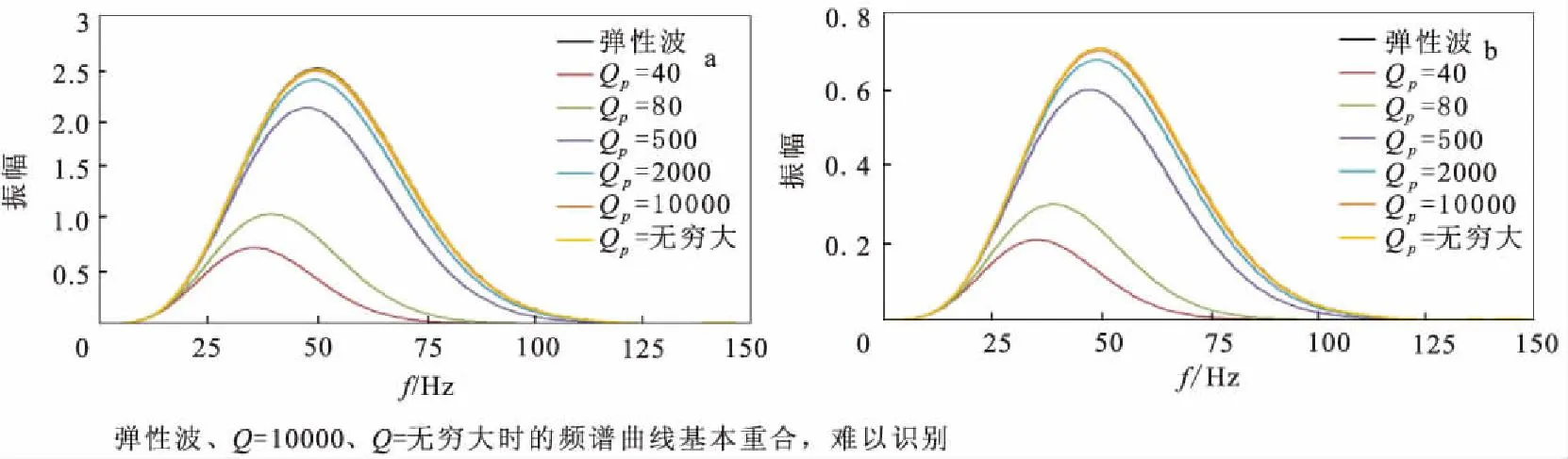
图9　PP反射波振幅谱与品质因子的关系Fig.9　The relationship between the amplitude spectrum and the quality factor of pp wave(a)垂直分量；(b)水平分量

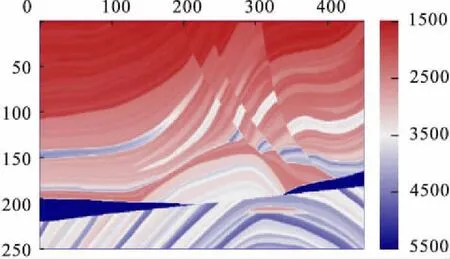
图10　Marmousi纵波速度模型Fig.10　Marmousi P wave velocity model

图11、图12是根据弹性波方程和粘弹性波方程正演得到的单炮记录。从图11、图12可以看出，在整个单炮记录上，粘弹性波动方程正演得到的单炮记录能量比弹性波方程的弱，从图11和图12中椭圆圈出来的部分可以明显看出，当品质因子为50时单炮记录的能量比品质因子为100时的单炮记录能量更弱。

3结论及讨论

作者用Kelvin粘弹性模型定性的模拟炸药震源激发后过渡区中地震波的传播特征，并与理想弹性介质中的地震波传播特征进行对比，分析品质因子Q对波传播特征的影响，得到了以下几点认识：

1)由于炸药震源爆炸后产生的过渡区具有类似于粘弹性介质的性质，在研究炸药震源爆炸产生地震子波机理时，不能忽略过渡区对波的吸收和衰减作用。

2)与弹性介质相比，粘弹性介质的PP反射波同相轴能量减弱，振幅衰减，且品质因子越小，衰减越严重，同时波形和相位也发生畸变。

3)与弹性介质相比，粘弹性介质的PP反射波主频降低，频宽变窄；随着品质因子的减小，主频向低频移动，频带也越窄。

4)当品质因子增大到一定程度的时候，介质的粘滞性对地震波的影响可以忽略；当其达到无限大时，粘弹性介质即退化为弹性介质。

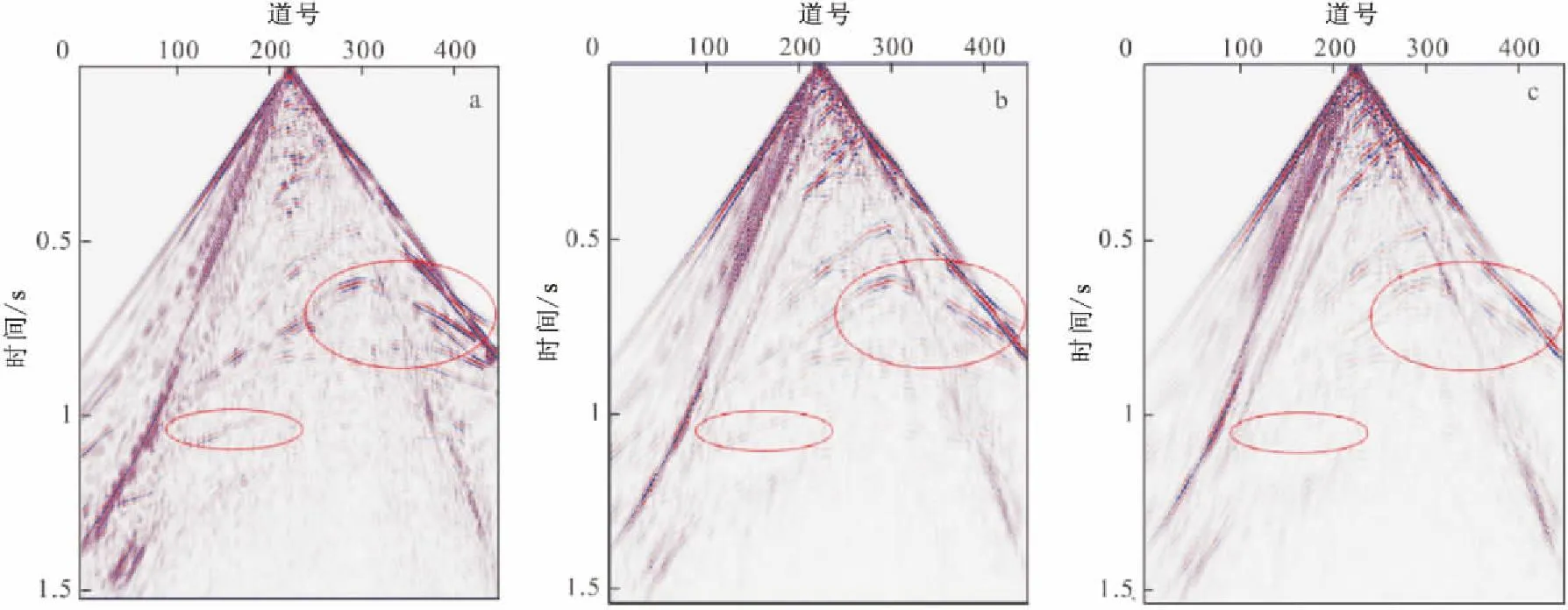
图11　Marmousi模型垂直分量单炮记录Fig11　Single shot simulated records of Marmousi model vertical component(a)弹性波单炮记录；(b)粘弹性波单炮记录(Qp=100)；(c)粘弹性波单炮记录(Qp=50)

图12　Marmousi模型水平分量单炮记录Fig12　Single shot simulated records of Marmousi model horizontal component(a)弹性波单炮记录；(b)粘弹性波单炮记录(Qp=100)；(c)粘弹性波单炮记录(Qp=50)

5)波在粘弹性介质中传播时，高频成分较低频成分衰减得更快。

通过对炸药震源激发过渡区的粘弹性特征的定性分析，一定程度上解释了近区能量快速衰减及地震资料主频低的原因。为了弄清楚介质的塑性变形和破碎对地震波的动力学影响，还应该建立更精确的物理量来描述过渡区介质的粘滞性，同时从弹塑性力学的角度分析应力应变的关系，从而给出准确的地震子波产生机理理论。

参考文献：

[1]SHARPE J A.The production of elastic waves by explosion pressures[J].Geophysics,1942,7(2)：144-154.

[2]BLODE F G.Spherical wave propogation in a sdici medium.Acoust.Soc.Am，1952,(24):211-215.

[3]肖建华,孙文涛.关于点爆炸震源产生 的地震子波[J].石油地球物理勘探,1997 ,32(6) :809-817.

XIAO J H,SUN W T.Seismic wavelet generated by point explosive source[J].Oil Geophysical Prospecting,1997,32(6) :809—817.(In Chinese)

[4]孙成禹,蔡纪琰.爆炸冲击波及地震子波的形成因素分析[J].石油地球物理探,2013,48(4) :513-518.

SUN C Y,CAI J Y.Explosive shock waves and factors generating seismic wavelets[J].Oil Geophysical Prospecting,2013,48(4) :513-518.(In Chinese)

[5]成景旺,顾汉明,徐照营.实际地层条件下爆炸震源子波模拟研究[J].工程地球物理学报,2009,6(5) :529-534.

CHENG J W,GU H M,XU Z Y.Simulation of Explosion Source Wavelet in the Actual Formation[J].Chinese Journal of Engineering Geophysics,2009,6(5) :529-534.(In Chinese)

[6]於文辉.地震勘探中震源机理的理论分析[J].石油物探,1992,31(1):24-28.

YU W H.Theoretical analysis of source mechanism in seismic prospecting[J].Geophysical prospecting for petroleum,1992,31(1):24-28.(In Chinese)

[7]任义庆,李勤学,马在田.地震爆炸震源模拟[J].石油物探,1998,37(3) :15-21.

REN Y Q,LI Q X,MA Z T.The Simulation of Seismic Explosive Source[J].Geophysical prospecting for Petroleum,1998,37(3) :15-21.(In chinese)

[8]FARROKH JALINOOS,J.E.White.Wave propagation from an explosive source[J].Geophysics,1986,51(3) :746-756.

[9]VICTORIA M.YARUSHINA,YURI Y.PODLADCHIKOV.Plastic yielding as a frequency and amplitude independent mechanism of seismic wave attenuation[J].Geophysics,2010,75(3) :51-63.

[10]奚先,姚姚.二维粘弹性随机介质中的波场特征分析[J].地球物理学报,2004,19(3) :608-615.

XI X,YAO Y.Forward modeling in the 2-D viscoelastic random medium[J].Progress in Geophysics,2004,19(3) :608-615.(In Chinese)

[11]牛滨华,孙春岩.半空间介质与地震 波传播[M].石油工业出版社,2002 .

NIU B H,SUN C Y.Half-space medium and seismic wave propagation[M] .Petroleum Industry Press,2002 .(In Chinese)

[12]何樵登.地震勘探原理和方法[M].北京：地质出版社,1986.

HE Q D.The Principle and Method of Seismic Exploration[M].Beijing:Geological Press,1986.(In Chinese)

[13]ZAHRADNIK J O,LEARY P AND SOCHACKI J.Finite-Difference schemes for clastic waves based on the integration approach[J].Geophysics,1974,39:834-842.

[14]孙成禹.地震波理论与方法[M].东营:中国石油大学出版社,2007 .

SUN C Y.Seismic Wave Theory and Method[M].Dongying:China University of Petroleum Press,2007.(In Chinese)

The analysis of the viscoelastic of medium in near area of explosive source excitation

CHEN Jie,ZHAI Kai-jing,QIN Long

(School of Geoscience and Technology,Southwest Petroleum University,Chengdu610500,China)

Abstract:In our country,an explosive source is the most commonly used excitation source in seismic exploration.Different partitions will be produced after the explosive,include cavity,transition zone and elastic zone.So far,to study how the seismic wave produced,the most commonly way is called “equivalent spherical cavity”，which ignores the impact of the transition zone.To descript the influence of cruse and permanent deformation of the transition area to the seismic wave qualitatively,the model can be simplified as viscoelastic model.In this paper,we deduce the phase velocity and the expression of Q based on the Kelvin viscoelastic model,then we use Kelvin viscoelastic model to forward modeling algorithm,and analyze the impact of quality factor Q on the basic frequency,amplitude and phase of seismic wave.The results show that the amplitude,frequency and phase of seismic wave are changed in the transition area,which provides a theoretical direction for the analysis of production of seismic wavelet,and also provides a theoretical basis for the analysis of seismic data collected in the actual medium.At the same time,it provides a meaningful actual value for the compensation of the influence on the viscosity factor and improving the quality of seismic data.

Key words:explosive source;Kelvin viscoelastic model;quality factor;numerical modeling;wave equation

收稿日期：2015-04-04改回日期：2015-05-25

作者简介：陈杰(1989-)，男，硕士，主要研究方向为应用地球物理方法和信号处理，E-mail:segzy520@yeah.net。

文章编号：1001-1749(2016)02-0252-07

中图分类号：P 631.4

文献标志码：A

DOI：10.3969/j.issn.1001-1749.2016.02.17