四两拨千斤

徐丽花

摘 要： 培养兴趣可以从对新奇事物的探究，巧设疑引发思考，在学生苦思冥想还不得要领之时，来个“山重水复疑无路，柳暗花明又一村”的欣喜，通过挖掘数学美、感受数学美，达到喜欢数学的目的，此外，通过变式训练，举一反三，理清问题的本质，提高学生的解题能力和运用数学的能力，也能增强信心；学有用的数学，能增强学生的应用意识，使学生变得乐学、好学，从而激发兴趣.

关键词： 数学教学 学习兴趣 教学方法

兴趣是开启智慧之门的金钥匙，是思维训练的突破口，在教学工作中，若能有效激发学生的学习兴趣，调动学生学习的积极性，将会对教学工作起到四两拨千斤的作用，那么采取什么方法激发学生学习的兴趣，从而调动学习的积极性呢？下面我谈谈在教学工作中的做法和体会.

一、设计惊诧，唤起兴趣

兴趣往往产生于对新奇事物的探究.苏霍姆林斯基说：“惊讶感情——是寻求知识的强大源泉.”因此尽量在学生面前展示一些有趣的新事物、新观点，或者一些稀奇惊讶的东西，驱使他们产生求知欲望.例如，在学习二次根式时，为更好地帮助学生纠错，我出示了一道证明题：请证明“1=2”，学生听后，先是惊讶，继而哗然，然后小组讨论.此时全班学生情绪高涨，这正是教师所期望得到的探究气氛.在“不愤不启，不悱不发”之际，我将证明过程写出：

四、感受唯美，提高兴趣

在教学过程中注意挖掘数学美的元素并将其展示给学生，让学生也能发现数学美，感知数学美.例如，在讲解一般三角形时，要把三角形的稳定美展示给学生，可以做一个三角形的支架模型和一个四边形的支架模型做比较.

学生会发现：当三角形的三边确定，它的形状、大小就固定下来了，而四边形的四边确定后，它的形状还会发生变化.而一般的三角形若加上一个条件：两条边相等，那么这个三角形是等腰三角形.很明显，等腰三角形有自身两边相等的匀称美.若沿顶角的平分线折叠，图形自身就会重合.由此发现它的一些性质：两条腰相等，两个底角相等，以及“三线合一”等.这样通过展示对称美，不仅能激发学生的学习兴趣，还能使他们比较直接地掌握教学内容.又如：不少数学概念、几何公理、定理的叙述，其语言的精炼美、形式的整齐美也随处可见，教学过程中若能点破其隐藏的数学美，对学生掌握数学知识是很有帮助的，如：公理“两点确定一条直线”“两点之间，线段最短”等，其语言简洁凝练，包含的内容却是十分丰富的.再如可以利用优化板书设计、运用现代教学手段，让数学美可视、可感、可知，培养学生对数学学习内容的兴趣.

五、变式求异，升华兴趣

通过一个问题的条件变式、结论变式、图形变式等能刺激学生的探索欲望，从而激发兴趣，调动学生学习的积极性.

例如课本上有这样一道题：求证：顺次连接任意四边形四边中点所得的四边形是平行四边形.讲完该题后，不失时机地进行变式，调动学生的思维兴趣.变式（1）顺次连接矩形四边中点所得四边形是什么图形？变式（2）顺次连接菱形四边中点所得四边形是什么图形？变式（3）顺次连接正方形四边中点所得四边形是什么图形？变式（4）顺次连接等腰梯形的四边中点所得四边形是什么图形？变式（5）顺次连接对角线相等的四边形的四边中点所得四边形是什么图形？顺次连接对角线互相垂直的四边形的四边中点呢？顺次连接对角线相等且互相垂直的四边形的四边中点呢？做完这一组练习后进一步引导学生概括，得出影响新图形形状的本质是“原四边形的对角线所具有的特征”.培养学生归类、总结的能力，达到调动学习积极性的目的.

又如应用题教学是初中数学教学中的一个难点，在教学中可以把同类型的题目通过变式的方式展现给学生，把学生的思维逐步引向深入.

例如在讲解《实际问题与一元一次方程》这节内容时，可以从奥运冠军刘翔与班级的一位跑步爱好者陈洁为题材编一道关于追及问题的应用题：陈洁与刘翔同在一起点，陈洁以每秒7米的速度先跑了30米，刘翔为了追上陈洁，他如果以每秒10米的速度跑多少秒才能追上陈洁？完成该题后再对本例做以下变式.

变式1：陈洁与刘翔同在起点，陈洁以每秒7米的速度先跑了30秒，刘翔为了追上快艇陈洁，他如果以每秒10米的速度跑多少秒才能追上陈洁？（从先行30米改为先行了30秒）

变式2：陈洁与刘翔同在起点，陈洁以每秒7米的速度先跑了30秒，刘翔想用55秒追上陈洁，他以每秒10米的速度跑了5秒后他发现用这样的速度不能在55秒内追上，请问他此时的想法对不对？如果他一定要在55秒内要追上，请你算一算刘翔后来要用多少速度才能在规定时间内追上陈洁？

这样的变式覆盖了同时出发相遇问题、不同时出发相遇问题、同时出发和不同时出发的追及问题等行程问题的基本类型.这样做一题通一类，弄清了问题的本质，今后碰到类似问题学生思维指向必定准确，很好地培养了学生思维的深刻性.

变式3：我们学校操场有300米的环形跑道，在比赛时经常会涉及相遇问题和追及问题.现有班上甲、乙两人比赛跑步，甲的速度是8米/秒，乙的速度是6米/秒，他们两人同地出发，

（1）若两人同时相向而行经过几秒两人相遇？

（2）若两人同时同向而行经过几秒两人第一次相遇？

（3）若乙先出发5秒，然后甲开始出发，问甲经过几秒两人第一次相遇？

变式3为学生熟悉的操场环形跑道问题，这三小题是一组变式题，（1）、（2）是同时同地出发的相遇和追及问题，（3）是不同时出发相遇和追及问题，本小题还蕴涵着分类讨论思想.

再如，原题：如图（1）正方形ABCD中，AE⊥BF，求证：AE=BF.

讲完该题后，可以进行以下几种变式探究：

现将BF平移至MN（如图（2），其他条件不变，问：此时MN与AE有怎样的位置关系？当学生回答出“垂直”以后，再给出如下变式题，即

变式1：如图（2），正方形ABCD中，MN⊥AE.此时MN=AE成立吗？若成立，给予证明；若不成立，说明理由.

再将AE作类似平移，即

变式2：如图（3）正方形ABCD中，MN⊥GH.

求证：MN=GH.

讲完后再进行如下变式：

变式3：如图（4），点H在正方形纸片ABCD的一边上，将纸片折叠，使点H正好与其所在边的对边上一点G重合，若折痕MN长为10cm，试求GH的长度，并说明理由.

通过不断变式，引发学生多方思考，触类旁通，培养发散思维能力，调动学生学习的积极性.

六、学以致用，保持兴趣

学有用的数学，是新课标的基本要求之一，数学在日常生活、工农业生产及现代科学技术中都有着重要而广泛的应用，授课时有意识地联系所学内容，有的放矢地介绍日常生活和科学领域中所用到的数学知识，或给出实际问题，利用数学知识解答，如学完三角形全等的有关知识后，告诉学生我们学校校内有一底部不能到达的建筑物，要想知道A、B两点间的距离（如图a），用什么方法可以做到？由于是实际问题，且建筑物就是学生熟悉的校园内的事物，学生讨论起来积极性特别高，他们跃跃欲试，也有准备下课后立即到实地测量的，在学生充分讨论，教师适时点拨之后，不难得出如图b的方法：在能同时到达A、B的地面上取一点O，连接AO并延长至C，使OC=OA，连接BO并延长至D，使OD=OB，连接CD，通过证明△OCD≌△OAB知，只需测量CD的长就能知道A、B两点间的距离.讲完之后，还可以告诉学生，随着将来所学知识的增多，方法也会越来越多.如，利用三角形的中位线或成比例线段等，进一步激发学生探求知识的欲望.此外，还能通过一些方案设计（如最短距离、最省费用等）题型让学生感受数学的广泛应用，保持及提高学生对数学的兴趣.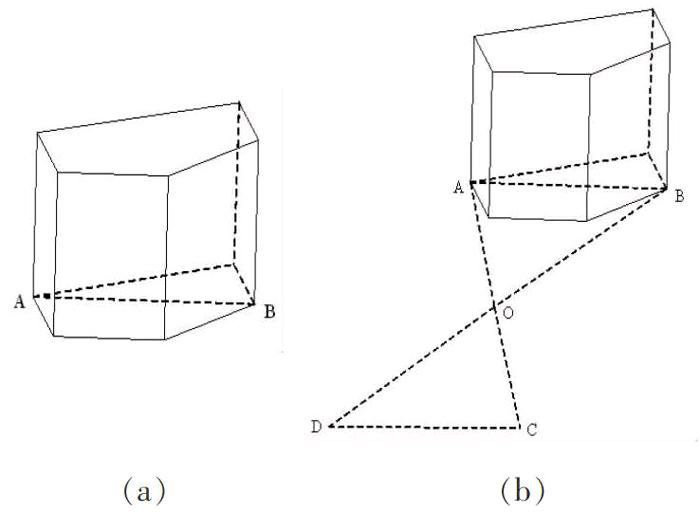

总之，只要充分培养学生的学习兴趣，才能真正调动学生学习的积极性.培养兴趣的方法很多，关键是教师要有足够的热心、爱心、耐心、信心，一定能找到适合自己、适合学生的好方法.

参考文献：

[1]李春山.中小学校本研究管理与实践.重庆大学出版社，2006.

[2]王尚志.数学教学研究与案例.高等教育出版社，2006.

[3]叶澜.教育研究方法论初探.上海教育出版社，2014.

[4]义务教育数学课程标准（2011年版）.