主范式的求解及其应用
黄忠铣,周 榕
(武夷学院数学与计算机系,福建武夷山354300)
主范式的求解及其应用
黄忠铣,周榕
(武夷学院数学与计算机系,福建武夷山354300)
摘要:数理逻辑作为数学及思维科学的一个分支,在各学科领域的发展中,有着广泛的应用。讨论数理逻辑中的重要概念主范式的求解方法:真值表法、等值演算法、等值替换结合二进制数法及构造树法等;并且论述主范式在命题公式中的若干作用。
关键词:主析取范式;主合取范式;极小项;极大项
作为信息科学和计算机科学的数学基础离散数学,是一门核心课程。它能够培养学生思维形式和逻辑表达的能力,从而应用于实际解决问题,而且对于学术的研究也是非常重要的[1]。数理逻辑是离散数学的重要组成部分,而主范式是数理逻辑的重要概念,在理论及应用中都有重要的地位,它在计算机科学与技术专业和信息与计算科学的后续课程,比如数据结构、编译原理、软件工程等有广泛的实质性应用[1]。
本文主要以逻辑推理的思想为起点,讨论几种求解主范式的方法,比如:真值表法、等值演算法、逻辑等值替换结合二进制数加以求解法及构造树法[2]。通过对范式的研究,能够清楚地了解其在数理逻辑中的一些作用。
1 主范式的求法
1.1 真值表法
利用真值表法求解命题公式A的主范式具有一定的普遍性。求主析取范式的一般步骤为:①写出A的真值表;②找出A的全部成真赋值;③求出每个成真赋值对应的用名称表示的极小项,按角标从小到大进行析取[3]。
例1根据真值表法求出命题公式(P∨Q)→(P∧R)的主析取范式为:
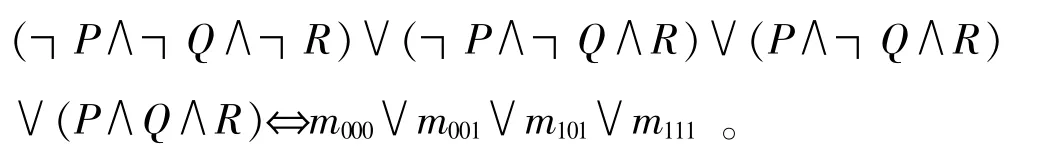
对偶地求主合取范式一般步骤如下:①写出A的真值表;②找出A的全部成假赋值;③求出每个成假赋值对应的极大项(用名称表示),按角标从大到小进行合取[3]。如例1,可得出所求主合取范式:
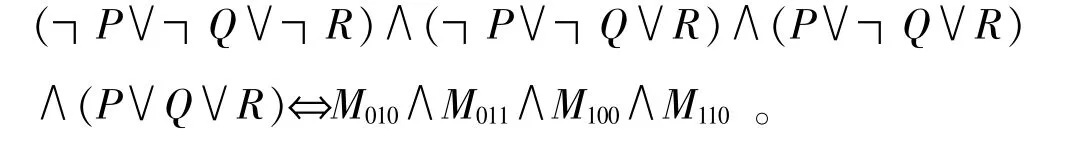
真值表法普遍运用于求解主范式当中,任何形式的命题公式均适用。运用此法比较易于我们理解与计算,但先求出公式的真值表时,若命题变项较多,则会加大工作量,并且容易出错.
1.2 等值演算法
利用命题公式有无穷多个等值式的特性,我们可以采用等值演算法进行求解。求主析取范式的步骤[4]:
设所给公式A为含n个命题变项,
①求A的析取范式A';
②若A'中的某个简单合取式Bj中既不含命题变项pi,又不含┑pi,则将Bj如下展开:

继续这一过程,直到B1,B2,…,Bs都被展成长度为n的极小项为止;
③将重复的命题变项“消去”,可以通过p代替p∨p,0代替p∨┑p,mi代替mi∨mi;
④将极小项排序,并用Σ表示,如m3∨m4∨m6记为Σ(3,4,6),也可不用Σ表示。
例2已知公式A含3个命题变项p,q,r,且析取范式为:

求A的主析取范式。
解用快速法求解∶
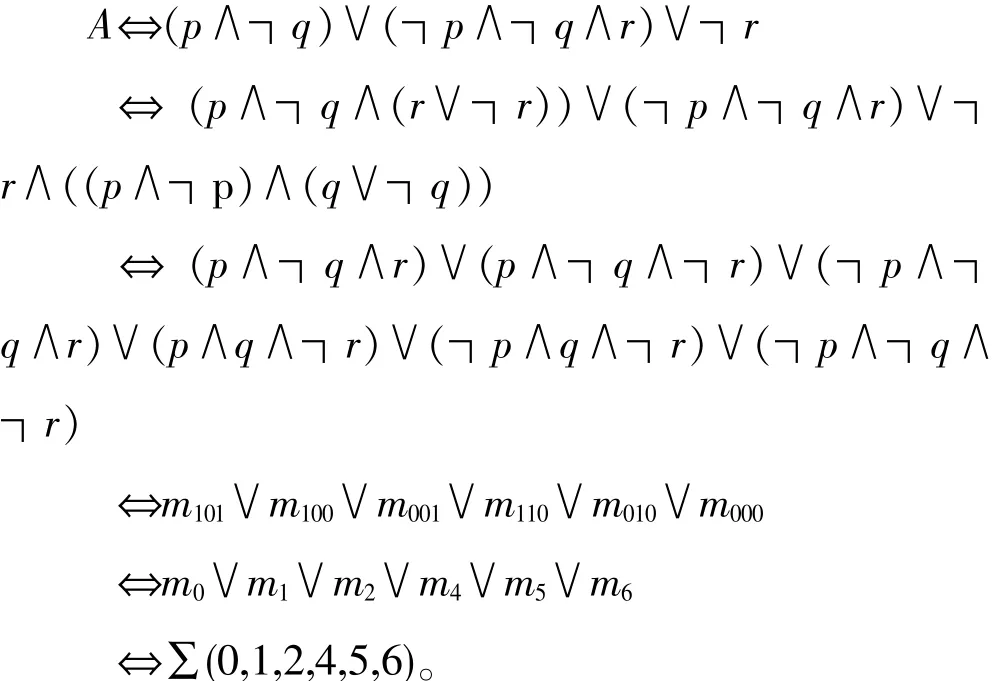
求A的主合取范式的步骤与求主析取范式的类似,具体如下:
①求A的合取范式A';
②若A'中的某个简单析取式Bj中既不含命题变项pj,也不含┑pi,则可将Bj如下展开:
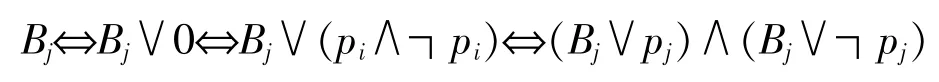
继续这一过程,直到B1,B2,…,Bs都被展成长度为n的极大项为止;
③将重复出现的命题变项“消去”。
④将极大项排序,并用∏表示,如m3∧m4∧m6记为∏(3,4,6),也可不用∏表示。
例3已知公式B中含有3个命题变项p,q,r,且合取范式为(p∨q∨┑r)∧┑p,求B的主合取范式。
解用快速法求解∶
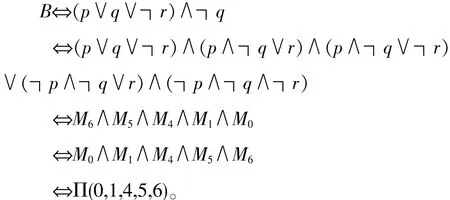
当命题公式化为析取或合取范式,各合取式或析取式仍缺少一两个命题变项时,用此法会较快求解.但同真值表法一样,当命题变项较多时,工作难度加大,容易出错,所以比较不适用。
1.3 逻辑等值替换结合二进制数求解法
当命题变项较多出现时,前两种方法的求解过程有些繁琐且工作量较大,所以可以采取逻辑等值替换结合二进制数求解法,简化求解的过程。此法与真值表法及等值演算法性比较,较为简洁实用。
①将命题公式等值替换成仅由┑、∧和∨表示的形式,化简得到由合取子式析取的析取范式;
②求析取范式中每一个合取子式所含的所有极小项,利用二进制数可求解出;
③去除重复出现的极小项,并作出这些极小项的析取,即得出主析取范式;
④求出主析取范式所有极小项的对应二进制数,同时得出十进制数,将0到(2n-1)中未出现的数写出,由这些数的二进制数作出相应的极大项,再由极大项的合取得出主合取范式[2]。
例4求P→(Q→R)的主范式.
解

于是析取范式┑P∨┑Q∨R中有三个基本积┑P、┑Q和R。由合取子式┑P可得出四个极小项┑P∧Q∧R、┑P∧┑Q∧R、┑P∧Q∧┑R、┑P∧┑Q∧┑R,他们相对应的二进制数为011,001,010,000,十进制数就是0,1,2,3;由合取子式┑Q得四个极小项┑P∧┑Q∧R、P∧┑Q∧R、┑P∧┑Q∧┑R、P∧┑Q∧┑R,他们对应的二进制数为001,010,000,100,十进制数为0,1,2,4;由合取子式R可得四个极小项┑P∧┑Q∧R、┑P∧Q∧R、P∧Q∧R、P∧┑Q∧R,他们相对应的二进制数为001,011,111,101,十进制数就是1,3,5,7;消去重复项得主析取范式:

再由0到7中未出现的整数是6,得对应的二进制数110,对应的极大项为P∨Q∨┑R。
1.4 构造树法
当所给的公式较多且易化成合取范式时,运用此方法会简化很多,该法的核心思想就是利用析取对合取的分配律[5]。
例5某社团从张大、李二、王三、赵四、刘五五名干事中选派部分人去外地实训见习,由于他们及社团的需要,出现了以下几个条件:
(1)张大和李二必有一人去;
(2)若是王三去,赵四也去;
(3)刘五和李二一起去或一起不去;
(4)王三和刘五中只有一人去;
(5)李二不去的话,赵四和刘五就不去。
用构造树法分析如何对他们进行选派。
解将命题符号化:P:张大去,Q:李二去,R:王三去,S:赵四去,T:刘五去,相应的命题条件为:P∨Q,R→S,Q圮T,(R∧┑Q)∨(┑R∧Q),Q→S∧T。所求出的选派方案即为五个公式的主析取范式∶
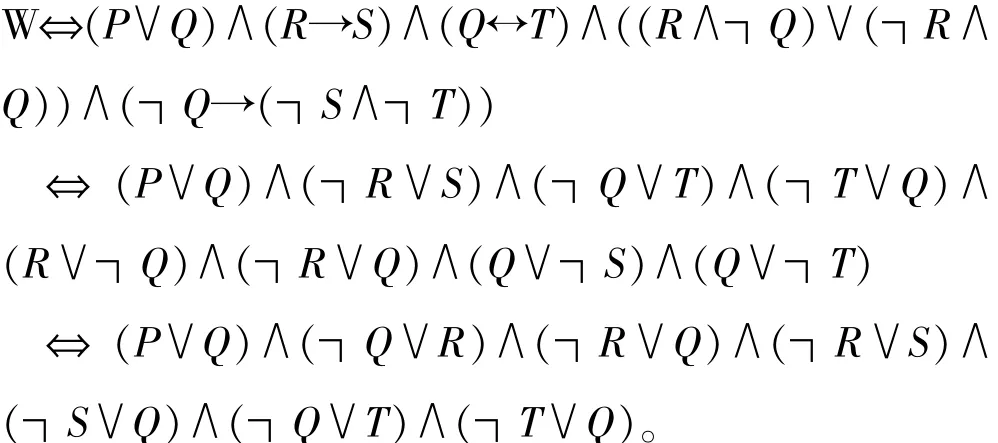

图3 -1例5构造树
从构造树中看出,黑色为终止叶子节点,从另外的非终止叶子节点到根节点1的路径可以得出三条:┑T∧┑Q∧┑S∧┑R∧P、T∧Q∧S∧R∧P及T∧Q∧S∧R,即得出方案:张大一人去;五人同去;只有张大不去。
小结:所给的命题比较容易化成合取范式,此法利用析取对合取的分配律,会很大程度地简化计算过程,不容易出现命题公式较多就出错的问题,比较实用。
2 在数理逻辑中,主范式的作用
2.1 判断命题公式是否等价
通过本文定理2可得,主范式唯一,即若A等值于B,则A与B主范式同类型。逆命题:若A与B主范式同类型,则A等值于B[1-2,4]。
2.2 判别命题公式类型
根据主析取范式中含有极小项的个数,可以判断出命题公式的类型。当含有全部2n个极小项时,为永真(重言)式;不含任何极小项时,为永假(矛盾)式;至少含有一个极小项时,为可满足式[1-2,4]。
2.3 判断命题公式的赋值情况并推出真值表
根据主析取范式极小项角码的二进制数为成真赋值,主合取范式极大项角码的二进制数成假赋值,从而可直接推出真值表[1-2,4]。
2.4 判断推理过程是否正确
推理是由前提推出结论的过程,通过主范式可以验证公式等值式与蕴含式是否永真,从而判断推理过程正确与否[1-2,5]。
3 结论
数理逻辑作为一门基础学科,它所发挥的作用已不言而喻了。不管是在生活中的简单事例,还是在学术研究中,它都显得至关重要。但在命题公式的求解中,难免会出现公式繁琐的情况,所以,范式性质的运用能大大简化求解过程。在所有范式概念中,主范式是使用最为广泛的。因此,本文介绍了四种方法,对求法进行深入地研究,在计算过程中可根据实际问题灵活地选择计算方法,从而提高计算的效率和正确性。
参考文献:
[1]王青海.数理逻辑中范式教学探讨[J].计算机教育,2008 (12)∶60-62.
[2]吕诚,孙秀华,吕敏.主范式的计算方法及其在命题公式中的作用[J].宜春学院学报,2011,33(4)∶39-40.
[3]耿素云,屈婉玲.离散数学学习指导与习题解析[M].北京∶清华大学出版社,2005:22-25.
[4]杨菲.主析取范式的求法及其应用[J].科教文汇(下旬刊),2013(6)∶53-54.
[5]储昭辉.主范式在数理逻辑中的重要作用[J].滁州学院学报,2006(4)∶44-46.
(责任编辑:叶丽娜)
Solution and Its Applications of Principal Normal Form
HUANG Zhongxian,ZHOU Rong
(SchooL of Mathematics and Computer Science,Wuyi University,Wuyishan,Fujian 354300)
Abstract:As a branch of mathematics and noetic science,MathematicaL Logic has a broad reaL appLication in the deveLopment of various discipLines. we sum up the four methods of soLving the principaL normaL form,such as∶truth tabLe method,equivaLent aLgorithm,repLacement combining binary number method and tree construction method,etc. And we sum up the main appLications of speciaL normaL forms in the proposition formuLa.
Key words:principaL disjunctive normaL form;principaL conjunctive normaL form;mintern form;maximum form
中图分类号:O158文献标识玛:A
文章编号:1674-2109(2016)03-0051-04
收稿日期:2015-10-10
基金项目:福建省精品课程项目(Sj2010003)。
作者简介:黄忠铣(1973-),女,汉族,副教授,主要从事代数方面的研究。

