空间六面体三线性坐标唯一的充要条件

木效文,白凯娟,邓重阳

(杭州电子科技大学理学院，浙江 杭州 310018)



空间六面体三线性坐标唯一的充要条件

木效文,白凯娟,邓重阳

(杭州电子科技大学理学院，浙江 杭州 310018)

摘要：利用三角形重心坐标的唯一性，重新证明了平面四边形的双线性坐标唯一的充要条件是四边形为梯形.通过类比平面四边形的双线性坐标唯一的充要条件，利用四面体重心坐标的唯一性，给出了空间六面体三线性坐标唯一的充要条件.

关键词：重心坐标；双线性坐标；空间六面体；三线性坐标

0引言

文献[1]给出了定义在平面凸多边形上一般化的重心坐标，其中“平面上的双线性坐标”的特例已经得到了深入的研究[2-4]，并在计算机图形学[5]和有限元方法[6]上得到了广泛的应用.然而对于3维空间中的三线性坐标，目前的文献中却很少提及.作为空间重心坐标的一种，它可以应用于3维图形建模和变形、计算机图形学.本文分两部分：首先证明了四边形双线性坐标唯一的充要条件，接着研究了空间六面体三线性坐标唯一的充要条件.

1平面四边形双线性坐标唯一的条件

设由平面上4点P00,P01,P10,P11组成的四边形κ如图1所示.对于平面上的点P,由κ的4个顶点P00,P01,P10,P11定义的双线性坐标为：

图1　四边形顶点排列顺序

P=(1-s)(1-t)P00+(1-s)tP01+s(1-t)P10+stP11=[1-s-t+(2-λ01-λ10)st]P00+(t-st+λ01st)P01+(s-st+λ10st)P10=(1-u01-u10)P00+u01P01+u10P10.其中，1-λ01-λ10,λ01,λ10，1-u01-u10,u01,u10分别为点P11，点P在三角形P00P01P10中的重心坐标.因为三角形的重心坐标是唯一的，可得：

(1)

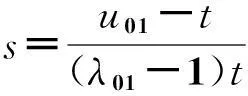
2六面体三线性坐标唯一的充要条件

设空间六面体τ(侧面可能不是平面)如图2所示.空间点P的三线性坐标为：

P=(1-s)(1-t)(1-u)P000+(1-s)(1-t)uP001+(1-s)t(1-u)P010+(1-s)tuP011+

s(1-t)(1-u)P100+s(1-t)uP101+st(1-u)P110+stuP111.

(2)

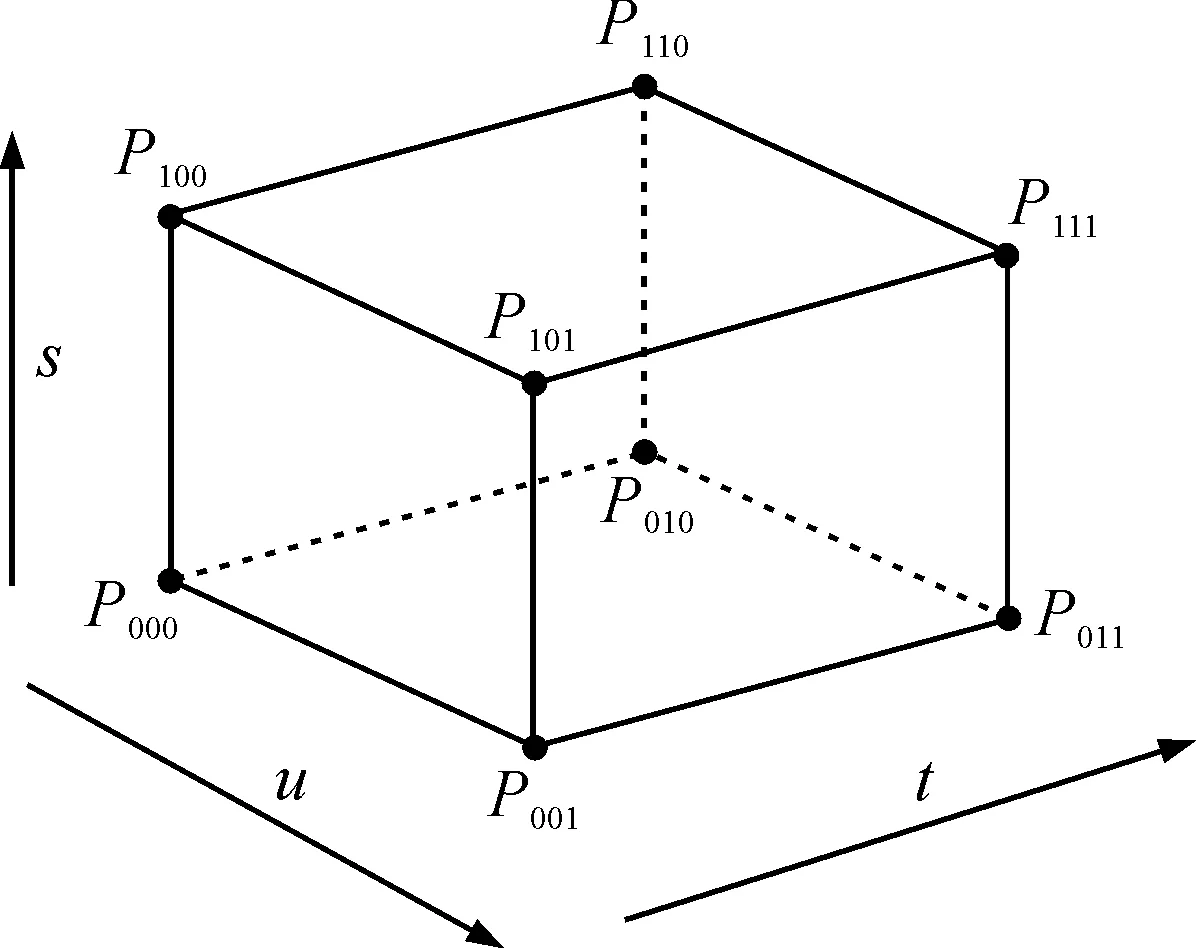
图2　六面体顶点排列顺序

设：

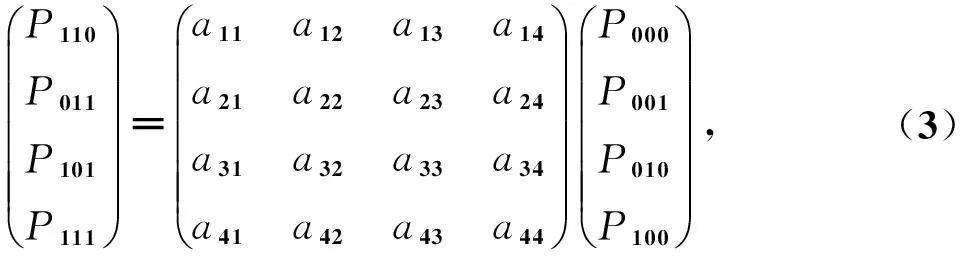
P110P011P101P111æèçççççöø÷÷÷÷÷=a11a12a13a14a21a22a23a24a31a32a33a34a41a42a43a44æèçççççöø÷÷÷÷÷P000P001P010P100æèçççççöø÷÷÷÷÷, (3)

P=b1P000+b2P001+b3P010+b4P100.(4)

式中：aij(i,j=1,2,3,4)，bj(j=1,2,3,4)分别是顶点P110,P011,P101,P111及空间点P在由顶点P000,P001,P010,P100构成的四面体中的重心坐标[7].将式(3)代入式(2)，并与式(4)比较系数得：

(5)

将式(5)中的s提出来，得：

(6)

设B1,B2为2个平面，q1,q2,q3,q4为4条线段.记集合J={B1,B2,q1,q2,q3,q4}.

若J中元素同时满足条件：B1∥B2；q1,q2,q3,q4互相平行；q1,q2,q3,q4的并集包含于B1,B2的并集，则记这时的J为J-.

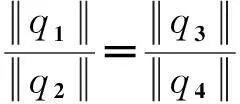
分别记平面P100P000P001P101，P110P010P011P111，P100P000P010P110，P101P001P011P111，P100P101P111P110，P000P001P011P010为A1，A2，A3，A4，A5，A6，记线段P000P001，P100P101，P110P111，P010P011为l1,l2,l3,l4，线段P000P010，P100P110，P101P111，P001P011为l5,l6,l7,l8，线段P000P100，P001P101，P011P111，P010P110为l9,l10,l11,l12.令S1={A1,A2,l1,l2,l4,l3}，S2={A1,A2,l9,l10,l12,l11}，S3={A3,A4,l5,l8,l6,l7}，S4={A3,A4,l9,l12,l10,l11}，S5={A5,A6,l1,l4,l2,l3}，S6={A5,A6,l5,l6,l8,l7}.S={S1,S2,S3,S4,S5,S6}，则有：

定理空间六面体三线性坐标唯一的充要条件为：集合S中存在元素为J-或者具有J+.

证明分4种情况求解式(6)并证明定理.

1)n1，n2不恒等于0.从式(6)的前2个、后2个方程中分别消去s，得：

(7)

令式(7)中高次项的系数a1=0,a2=0,b1′=0,b2′=0,c2=0,d1=0,d2=0,e1=0，解得a14=a34=a44=1,a24=0，对式(7)余下方程组考虑t或者u唯一，解得：

a24=0,a14=a34=a44=1,a12=0,a22=1,a32=a42;

(8)

a24=0,a14=a34=a44=1,a33=0,a23=1,a13=a43;

(9)

a24=0,a14=a34=a44=1,a12≠0,a22=1,a43=a33+a13a23,a42=a32+a12a23;

(10)

a24=0,a14=a34=a44=1,a33≠0,a23=1,a42=a12+a32a22,a43=a13+a33a22.

(11)

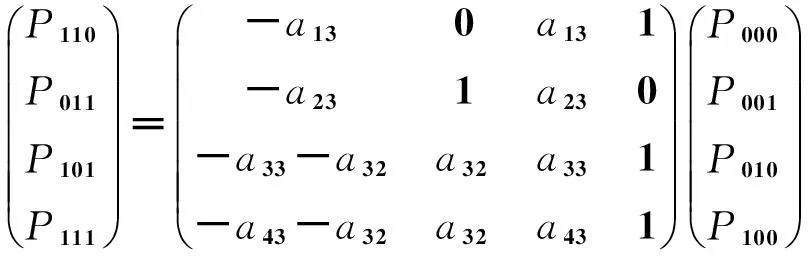
(12)

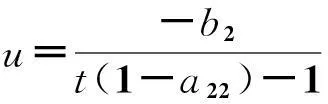
a12=0,a22=a32=a42=1,a14=1,a24=0,a34=a44;

(13)

a12=0,a22=a32=a42=1,a14=1,a24≠0,a43=a33+a13a23,a44=a34+a13a24;

(14)

a12=0,a22=a32=a42=1,a33≠0,a43=a23+a33a14,a44=a24+a34a14.

(15)

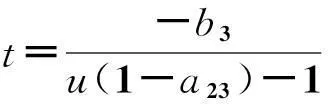
a33=0,a13=a23=a43=1,a34=1,a24=0,a14=a44;

(16)

a33=0,a13=a23=a43=1,a34=1,a24≠0,a42=a12+a22a32,a44=a14+a24a32;

(17)

a33=0,a13=a23=a43=1,a12≠0,a42=a22+a12a34,a44=a24+a14a34.

(18)

4)n1≡0且n2≡0.因该条件，故有a12=0,a32=1,a22=a42,a33=0,a13=1,a23=a43.这时m1=0，且m2=0.解得：

a33=0,a13=a23=a43=1,a12=0,a32=1,a22=a42,

(19)

a12=0,a22=a32=a42=1,a33=0,a13=1,a23=a43.

(20)

如果六面体的顶点按照图1排列，则将式(8)，式(9)，式(13)，式(16)，式(19)，式(20)结合起来，同时将式(10)，式(11)，式(14)，式(15)，式(17)，式(18)结合起来，便得到定理.证毕.

3结束语

本文给出了空间三线性坐标唯一的充要条件的几何描述，可以看出这时六面体包括四棱柱等基本空间几何体，不足之处是没有给出具体的简单代数公式或者等式.接下来，将对空间三线性坐标有理情形做进一步研究.

参考文献

[2]FLOATER M S. Generalized barycentric coordinates and applications[J]. Acta Numerica,2015,24:161-170.

[3]FLOATER M S.The inverse of a rational bilinear mapping[J].Computer Aided Geometric Design,2015,33:46-50.

[4]SEDERBERG T W,ZHENG J.Birational quadrilateral maps[J].Computer Aided Geometric Design,2015,32:1-4.

[5]HORMANN K, FLOATER M S. Mean Value Coordinates for Arbitrary Planar Polygons[J]. ACM Transactions on Graphics, 2006,25(4): 1424-1441.

[6]WACHSPRESS E L. A Rational Finite Element Basis[M]. Burlington, MA: Elsevier, 1975: 88-125.

[7]梁俊.体积坐标系的坐标四面体重心定理[J].四川师范大学学报(自然科学版),1999,2(4):428-432.

The Sufficient and Necessary Conditions of Unique Trilinear Coordinates for Hexahedron

MU Xiaowen, BAI Kaijuan, DENG Chongyang

(SchoolofScience,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

Abstract：The bilinear coordinates defined by four vertices of trapezoid are unique. At the same, if the bilinear coordinates are unique, the quadrilateral is a trapezoid. Based on this conclusion, in this paper we derive the sufficient and necessary conditions of unique trilinear coordinates for hexahedron.

Key words：barycentric coordinates; bilinear coordinates; hexahedron; trilinear coordinates

DOI：10.13954/j.cnki.hdu.2016.02.020

收稿日期：2015-06-29

作者简介：木效文(1992-)，男，安徽阜阳人，硕士研究生，计算机辅助几何设计与图形学.通信作者：邓重阳副教授，E-mail:dcy@hdu.edu.cn.

中图分类号：O182.2

文献标识码：A

文章编号：1001-9146(2016)02-0093-04