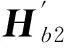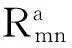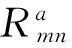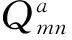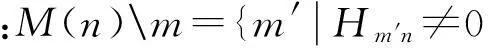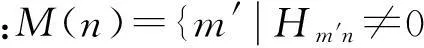多进制LDPC码编译码研究
陈志为
(中国电子科技集团公司第20研究所,西安 710068)
多进制LDPC码编译码研究
陈志为
(中国电子科技集团公司第20研究所,西安 710068)
摘要:低密度奇偶校验(LDPC)码是当前广泛应用的信道编码方式。多进制LDPC码在各类噪声的干扰下,纠错性能仍然极好,是如今信道编码学者重点研究方向。主要研究多进制LDPC码的编码和译码方法,通过软件仿真,分别对比不同编码和译码方法的纠错性能,并分析造成纠错性能差异的原因。主要对一种由二进制LDPC码中元素替换得到的四进制LDPC码,通过软件进行仿真分析,并最终得到5/6码率,采用16符号正交幅度调制(16QAM)方式的四进制LDPC码的编码结构。
关键词:信道编码;多进制低密度奇偶校验码;快速傅里叶变换-和积算法(FFT-SPA)译码
0引言
低密度奇偶校验(LDPC)码[1]的概念由Gallarger博士于1962年在其论文中提出[2],一并提出的还有最早的LDPC码的编译码方法,称为古典方法。但是由于当时落后的计算条件,学者并没有对LDPC码给予足够的重视。Mackay和Neal[3]对LDPC码进行了深入研究,并在1995年发现,经过改进的LDPC码译码算法,具有与Turbo码相当的性能,甚至在码长比较长时会超过Turbo码。这个重大发现立刻在整个编码界引发了重新研究LDPC码的热潮。2000年以后,经过全世界学者们的共同努力,人们发现比起传统的二进制LDPC码来,多进制LDPC码在同样信噪比条件下的误码率更低[4]。但是,多进制LDPC码的更低误码率是建立在过高的编译码复杂度和硬件复杂度的基础上,因此多进制LDPC码的发展遇到了前所未有的困难[5]。
本文针对多进制LDPC码的编译码算法进行仿真研究,通过软件仿真结果,说明多进制LDPC码在编码和译码算法不同时,其误码率性能也不同。再通过改变多进制LDPC码的码长和调制方式,来分析这些改变对码字性能的影响。
1多进制LDPC码的构造方法
多进制LDPC码可以通过对二进制LDPC码的校验矩阵中元素取值范围的改变来构造,由原来的FG(2)={0,1}变为FG(2m)={0,1,…,2m-1}。因此在多进制LDPC码中,一个码元表示的是一个以m个比特为总体的符号。本文采用IEEE 802.16e/D8中的构造方式进行二进制LDPC码校验矩阵H的构造,再以边缘熵最大为原则,对校验矩阵H中非零元素进行有限域FG(q)的替换[6],最终得到多进制LDPC码的校验矩阵H。IEEE802.16e/D8中LDPC码具有准循环的性质,其校验矩阵H的结构为:
(1)
式中:Pp(i,j)为z×z维矩阵,是全零矩阵或者由单位矩阵循环移位而来的矩阵,p(i,j)为单位矩阵循环右移次数。特别地,p(i,j)为-1时,代表Pp(i,j)为零矩阵。
校验矩阵H由基矩阵Hb进行矩阵扩展而形成。首先分别将基矩阵Hb中的0和1替换成-1和矩阵的循环右移的次数,得到的矩阵记为Hbm。再分别将矩阵Hbm中的-1和0扩展为z×z维零矩阵和单位矩阵,其余的元素扩展为循环移位矩阵,这样就可以得到最终的校验矩阵H。


(2)
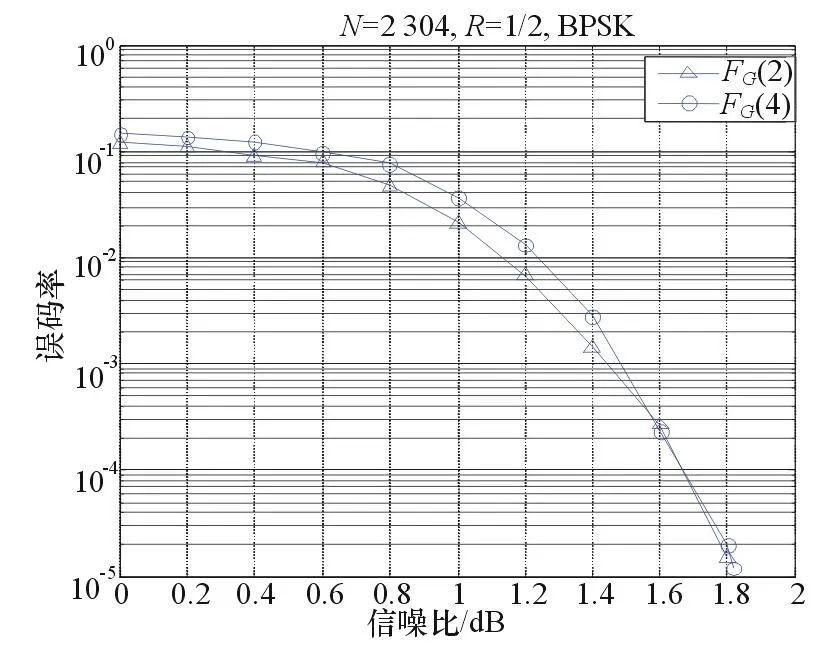
式中:hb(0)=hb(mb-1)=l,0≤l≤z,hb(i)=0,0 采用串行编码方法,将信息序列分成kb组,表示成u=[u(0),u(1),…,u(kb-1)],u中的每一个元素u(i)均为z维的列向量。校验矩阵Hbm在进行编码的时候,同样可以将校验序列v分成mb组z维的列向量,即v=[v(0),v(1),…,v(mb-1)]。具体的编码过程为: (1) 初始化,确定v(0) 把校验矩阵Hbm逐行相加,有: (3) 式中:1≤x≤mb-2,Pp(x,kb)表示由单位矩阵经过p(x,kb)次右循环得到的矩阵。 从而可以得到v(0),即: (4) (2) 递归计算,求v(i)的值 (5) (6) 用这个方法就可以计算得到所有校验比特v(i),i=1,2,…,mb-2的值。 2多进制LDPC码的快速傅里叶变化-和积算法(FFT-SPA)译码 假设采用二进制相移键控(BPSK)的调制方式,在加性高斯白噪声(AWGN)信道中传播。由于在多进制LDPC码中,每个符号可以取到的值范围是0,1,2,…,q-1,那么需要将每个符号变为二进制后,进行0→1,1→-1的映射。假设接收到的信号为yi,发送的信号为xi,ni是零均值、方差为σ2的高斯白噪声,于是有: (7) 高斯白噪声ni的概率密度函数(PDF)为: (8) 多进制LDPC码的FFT-SPA译码算法[7]具体步骤如下: (1) 初始概率计算 假设编码前每个符号出现概率相等,那么经转换的二进制序列中,0和1仍然是等概率的。以二进制形式来表示a=[a0a1…ap-1],ai∈{0,1},i=0,1,…,q-1。由于每个比特在传输中是相互独立的,那么: (9) 那么有: (10) (11) (2) 转置 (12) 式中:Hmn为校验矩阵H中第m行第n列的元素。 定义2个部分和的值,分别为: (13) (14) 根据部分和的定义,有: 颈椎轴性症状(axial symptoms,AS)评价采用四分法:优,术后无颈部不适症状;良,症状出现在劳累或受凉时,症状较轻,对生活工作影响不大,休息或卧位可缓解,无需服用止痛药物;可,症状出现较为频繁,但每年不超过约3个月,颈部可有压痛痉挛,服用止痛药物缓解;差,症状出现很频繁,超过3个月,颈部疼痛僵硬、麻木症状严重,止痛药物效果不佳。其中“优”和“良”定义为无轴性症状,“可”和“差”定义为有轴性症状【4】。 P(αm(n-1)+βm(n+1)+Hmna=0)= (15) (a) 对转置后的序列作FFT,有: (16) (b) 将FFT变换后的序列相乘,有: (17) (18) (4) 逆转置 逆转置是将转置运算的结果还原,相当于对有限域FG(q)上所有的元素除以Hmn。于是就有: (19) (20) (6) 计算后验概率,进行判决 后验概率为: (21) 3多进制LDPC码的对数似然比(LLR)-FFT-SPA译码算法 可以将多进制LDPC码的译码算法通过对数运算扩展到对数域[8],这样就把译码时的乘法运算变成了加法运算。定义对数似然比的形式如下: (22) (23) (24) (25) 4仿真结果及分析 将IEEE 802.16e中的二进制LDPC码(nb=24,kb=12,z=96,码长N=2 304,码率R=1/2=0.5)的校验矩阵H中非零元素进行有限域FG(q)的替换,得到码长N=1 192的四进制LDPC码。在调制时采用BPSK方式,噪声为AWGN信道,采用FFT-SPA算法进行译码,仿真结果如图1所示。 图1 LDPC码性能对比(0.5码率) 由图1可以看出四进制LDPC码的性能与原二进制码没有太大变化,仅仅在瀑布区下降速度更快。四进制的LDPC码比二进制的LDPC码拥有更大的编译码复杂度,但性能上没有提升,主要是由于以最大边缘熵原则进行非零元素替换得到的矩阵个数众多,此矩阵并不是使其能达到最优性能的矩阵。 改变以上条件下的参数,使kb=4,其他参数均不变,得到的是码长为N=1 152,码率为R=5/6=0.833 3的四进制LDPC码。在BPSK调制方式下,经过AWGN信道,仿真结果如图2所示。 图2 LDPC码性能对比(0.833 3码率) 编码速率由0.5提高到0.833 3,四进制LDPC码的误码率曲线已经在二进制LDPC码的左边较远的距离了。当误码率为10-5左右时,四进制LDPC码的信噪比约为2.80 dB,而二进制LDPC码的信噪比约为2.92 dB,性能提高约为0.12 dB。在实际应用中,0.12 dB的性能提升几乎感觉不到,但是多进制LDPC在高码率的情况下,其优势可见一斑。 如果采用16符号正交调幅(16QAM)的调制方式,重新对上面的四进制LDPC码进行仿真,仿真结果如图3所示。 图3 LDPC码性能对比(0.833 3码率,16QAM调制) 通过仿真结果可以看出,在码率提高到0.833 3之后,同时采用16QAM的高阶调制方式,多进制LDPC码的误码率曲线性能显著。在误码率为10-5左右时,四进制LDPC码的信噪比约为6.3dB,二进制LDPC码的信噪比约为7.1dB,二者差值约为0.8dB。通过与之前的仿真结果进行对比,说明多进制LDPC码在高码率、高阶调制方式的情况下,性能要比二进制LDPC码优越得多。 表1表示的是译码时的不同算法所需各种运算量的对比。 表1 多进制LDPC码译码算法运算量对比 接下来对比FFT-SPA和LLR-FFT-SPA2种译码算法。选取Mackay构造的基于有限域FG(4)上的四进制LDPC码,其参数为K=3 000,N=9 000,R=K/N=1/3,dc=4,dv=3。图4所示为2种译码算法的性能对比。 图4 四进制LDPC译码算法性能仿真比较 通过仿真结果可以看出,采用LLR-FFT-SPA算法的误码率曲线与之前的FFT-SPA算法的曲线大部分重合。在误码率为10-5左右时,2条曲线相差不到0.01dB,说明LLR-FFT-SPA算法在硬件复杂度大大降低的同时,只牺牲了不到0.01dB左右的性能,是一个好的算法。 5结束语 本文根据IEEE802.16e/D8中的二进制LDPC码,通过元素替换构造得到四进制LDPC码,比相应的二进制LDPC码性能有较大的提升,是一种在实际应用中可行的码字。 多进制LDPC码在高码率和高调制阶数的条件下,有比二进制LDPC码更好的纠错性能,但算法复杂度过高,导致实现时硬件复杂,是目前制约多进制LDPC码发展的最大阻碍,也是在未来研究中需重点攻克的难题。 参考文献 [1]GALLAGERRG.LowDensityParityCheckCodes[M].Cambridge,MA:MITPress,1963. [2]SHANNONCB.Amathematicaltheoryofcommunication[J].TheBellSystemTechnicalJournal,1948,27(3):379-423. [3]MACKAYD,NealR.Nearshannonlimitperformanceoflow-densityparitycheckcodes[J].ElectronicsLetters,1996,3(6):457-458. [4]DAVEYMC,MACKAYD.Low-densityparitycheckcodesoverGF(q)[J].IEEECommunicationsLetters,1998,2(6):165-167. [5]CALDERBANK A R.The art of signaling:fifty years of coding theory[J].IEEE Transactions on Information Theory,1998,44(6):2561-2595. [6]DECLERCQ D,FOSSORIER M.Decoding algorithms for nonbinary LDPC codes over GF(q)[J].IEEE Transactions on Communications,2007,55(4):633-643. [7]HAN G J,GUAN Y L,HUANG X M.Check node reliability-based scheduling for BP decoding of non-binary LDPC codes[J].IEEE Transactions on Communications,2013,61(3): 877-885. [8]DAVEY M C.Error-correction Using Low Density Parity Check Codes[D].Cambridge CB2 1TN,UK:University of Cambridge,UK,1999. Research into Encoding and Decoding of Non-Binary LDPC Codes CHEN Zhi-wei (The 20th Research Institute of CETC,Xi'an 710068) Abstract:Low density parity check (LDPC) code is a channel encoding mode commonly used at present.Non-binary (NB)-LDPC codes have great error correcting performance under various noises jamming,is an important research direction of channel encoding researchers.This paper mainly studies the encoding and decoding methods of NB-LDPC codes,compares the error correcting performance of different encoding and decoding methods through software simulation,and analyzes the reason leading to the difference of error correcting performance,mainly performs simulation analysis to 4-ary LDPC codes that are gained by replacing elements in binary LDPC,finally gains the encoding structure of 4-ary LDPC codes with the code ratio of 5/6 by using 16-quadrature amplitude modulation (16QAM) mode. Key words:channel encoding;non-binary low density parity check code;fast Fourier transform-sum-product algorithm decoding 收稿日期:2016-02-23 中图分类号:TN919.3 文献标识码:A 文章编号:CN32-1413(2016)02-0053-05 DOI:10.16426/j.cnki.jcdzdk.2016.02.014