紊流空间相关系数对大跨度三塔悬索桥抖振响应的影响

茅建校， 王　浩， 陶天友， 徐梓栋， 李爱群

(东南大学 混凝土及预应力混凝土结构教育部重点实验室，南京　210096)

紊流空间相关系数对大跨度三塔悬索桥抖振响应的影响

茅建校， 王浩， 陶天友， 徐梓栋， 李爱群

(东南大学 混凝土及预应力混凝土结构教育部重点实验室，南京210096)

摘要：鉴于紊流空间相关系数尚难以准确获取的现状，以泰州长江公路大桥为研究对象，采用谐波合成法模拟了该桥的三维脉动风场，并基于ANSYS平台进行了该桥非线性抖振响应时域分析。在研究过程中，以Davenport相干函数中的无量纲衰减因子λ为控制参数，重点分析了紊流空间相关系数对大跨度三塔悬索桥风致抖振响应的影响。研究结果表明，紊流空间相关系数对桥梁抖振响应影响较大，主梁跨中侧向与扭转位移响应随着衰减因子的增大而减小，竖向抖振位移响应随着衰减因子的增大而略有增加，且不同的衰减因子λ所造成的抖振响应计算值的差值可达50%以上。结论可供大跨度三塔悬索桥的风致抖振研究参考。

关键词：三塔悬索桥；紊流空间相关系数；抖振响应；风场模拟；相干函数

近年来，随着国民经济的增长以及现代材料和施工技术的发展，桥梁结构日益向着大跨、柔性、轻质和低阻尼的方向发展，在一些特殊情况下多塔悬索桥已成为设计必选方案之一[1]，其中尤以三塔双跨悬索桥方案备受工程师们的青睐。与两塔悬索桥相比，三塔悬索桥中间塔柱在纵桥向缺少重力式锚碇的强大约束，结构整体刚度急剧下降，使得桥梁结构对风荷载的敏感性显著增加。然而，目前大量的研究工作主要针对传统的两塔悬索桥而开展[2-5]作为一种新型桥梁体系，三塔悬索桥风致抖振研究目前尚无完善的资料可以参考，使得开展此类桥梁的风致抖振及其精细化研究工作尤为迫切。

紊流空间相关性是指同一时刻不同空间点脉动风速的相关性，常用紊流空间相关系数对其进行描述。紊流空间相关系数对工程结构的抗风设计与计算至关重要，然而由于紊流空间相关系数测试及分析工作的复杂性，使得获取准确可靠的紊流空间相关系数尚存在一定难度，紊流空间相关系数的研究工作也因此成为结构风工程领域的研究热点和基础性工作之一[6-13]。现场实测和经验公式是紊流空间相关系数研究中常用的两种取值手段，然而由于现场实测难度较大，且每次实测只能获得某次强风的相关性记录，使得该方法不具备通用性[14]。因此国际上目前普遍采用经验公式进行计算，并且提出了很多经验公式，其中以Davenport相干函数最为常用[2]。

在紊流空间相关性及其对结构风振的影响方面，国内外学者已采用理论分析、数值计算、风洞试验以及现场实测等手段进行了一些研究。例如，Larose[9]深入研究了不同湍流特性和不同高宽比的梁截面对桥跨方向抖振力分布的影响，据此提出了相关的经验公式。许志豪等[10]进行了不同风场下昂船洲大桥缩尺模型的风洞试验，并对抖振力沿桥跨方向相关性的衰减系数进行了拟合。黄东梅等[11]重点研究了大气边界层风速的竖向空间相干曲线，给出了修正的指数衰减函数，指出了用传统的简化指数衰减函数来进行拟合时在低频处的不足。于永帅[12]以某两塔钢桁架悬索桥为背景，研究了脉动风速空间相关系数对该桥主梁抖振位移的影响。Song等[13]以澳门友谊大桥为背景，采用两个三维超声风速仪基站对2008年的鹦鹉台风的紊流相关性进行了实测研究。然而至今为止，利用紊流空间相关系数对大跨度三塔悬索桥抖振响应影响的研究工作尚鲜见报道。

针对以上问题，本文选取泰州大桥为研究对象，基于Matlab编制程序，进行了该大跨度三塔悬索桥的三维随机脉动风场的模拟，在此基础上利用ANSYS建立了该桥的三维空间有限元模型，并进行了其抖振响应的非线性时域分析。其中以我国《公路桥梁抗风设计规范》所采用的Davenport指数衰减模型为对象，通过变化衰减因子λ取值，重点研究了紊流空间相关系数对大跨度三塔悬索桥抖振响应的影响，以期推进大跨度三塔悬索桥抖振响应的精细化研究，为该类型桥梁的抗风设计及研究提供参考。

1工程背景

泰州长江公路大桥位于江苏省境内长江中段，为三塔双跨悬索桥，主跨跨径布置为2×1 080 m，两锚相距2 940 m(见图1)。泰州大桥为世界首座千米级三塔悬索桥，也是目前世界上最大跨度的三塔悬索桥，国内首次采用人字形钢塔，具有世界上最大的沉井基础。其加劲梁采用封闭式流线型扁平钢箱梁，加劲梁设上斜腹板及下斜腹板构成导风嘴。钢箱梁节段标准长度为16 m，中心线处梁高3.5 m。主缆在设计成桥状态矢跨比为1/9，两根主缆横向间距为35.8 m。桥塔均采用门式框架结构，两边塔为混凝土结构，顺桥向呈单柱形；中塔为钢结构，顺桥向呈人字形，以增强纵向刚度。

图1　泰州长江大桥结构布置图(m)Fig.1 Layout of Taizhou Yangtze River Bridge (m)

2泰州大桥有限元模型

基于大型有限元分析软件ANSYS平台建立了泰州大桥的有限元计算模型，如图2所示。其中加劲梁采用鱼骨梁式简化模型，加劲梁和桥塔等构件简化为空间梁单元，加劲梁按吊杆的吊点进行离散。主缆、吊杆则简化为空间杆单元，主缆按吊杆的吊点进行离散，其弹性模量采用Ernst等效弹模公式进行计算。根据结构设计，耦合了主梁与边塔在竖向、横桥向以及绕顺桥向的转动自由度，并耦合了主梁与中塔在横桥向的自由度。由于该桥基础刚度足够大，在保证精度的同时为了简化计算，主缆和桥塔底部完全固结，未考虑土-桩-结构相互作用[15]。

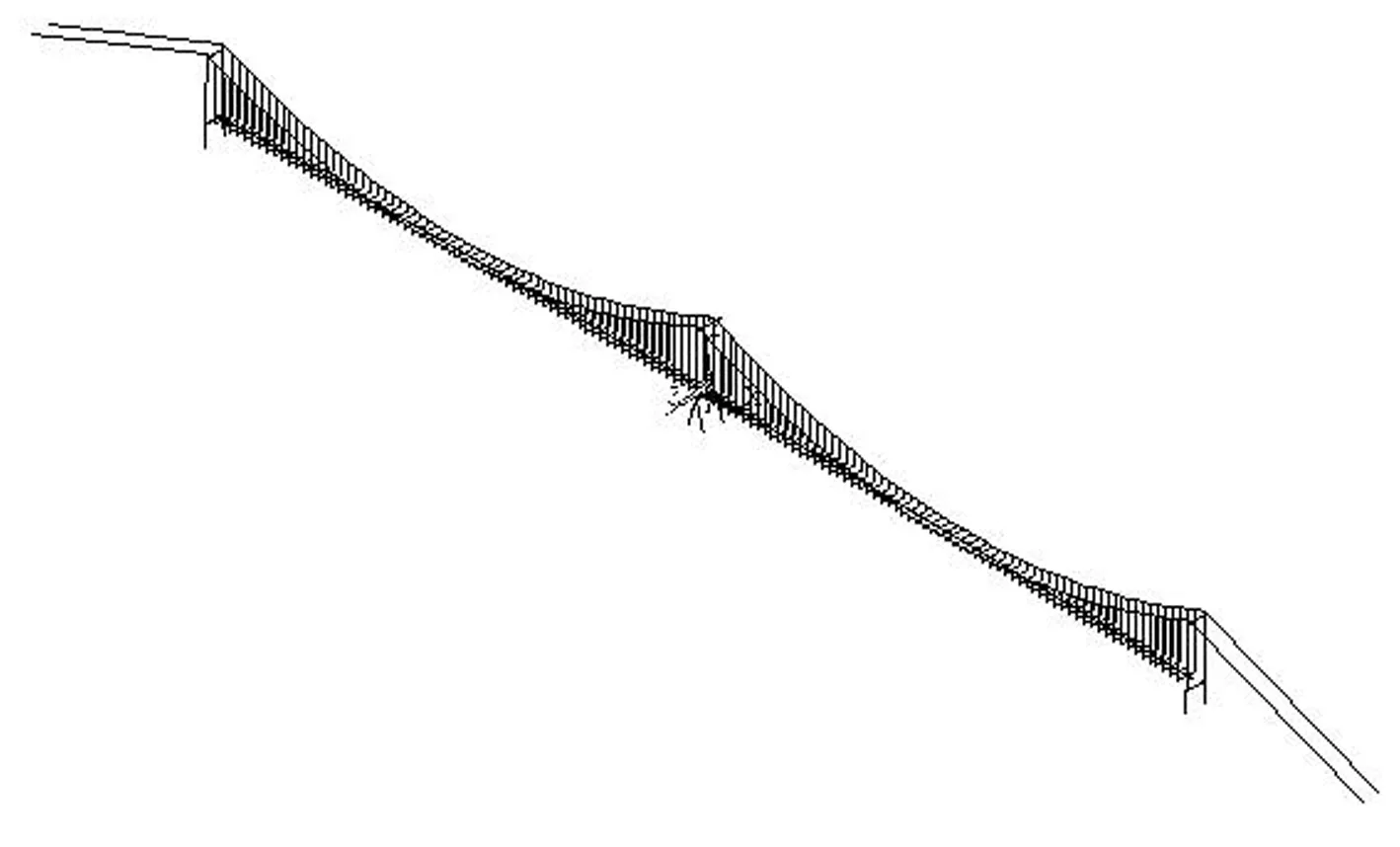
图2　泰州大桥空间有限元计算模型Fig.2 Spatial finite element(FE)model of taizhou bridge

3泰州大桥三维脉动风场模拟

3.1风场简化

考虑到泰州大桥主梁为顺桥向线状结构，可忽略顺桥向脉动分量v的作用；桥塔为竖向线状结构，且主缆对其约束较强，可仅考虑横桥向脉动分量u的作用。因此，该桥三维脉动风场可简化5个独立的一维多变量随机风场，如表1所示。其中主梁沿跨度方向80 m等间距分布、主塔沿竖向30 m等间距分布，模拟点分布如图3所示。

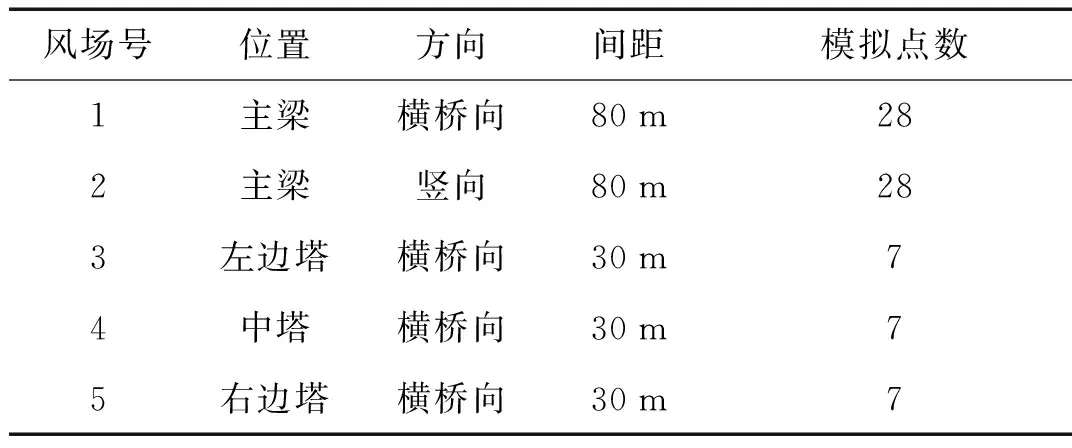
表1　简化的5个独立的一维脉动风场

图3　三维脉动风场模拟点布置 (m)Fig.3 3D fluctuating wind field simulation points arrangement (m)

该桥三维脉动风场模拟时，采用Davenport提出的指数衰减模型描述脉动风速的空间相关性[2]，其中空间相关函数Cohij(f)的近似表达式为：

(1)

3.2主梁风场模拟

采用谐波合成法模拟了该桥主梁的三维脉动风场[7,16]，根据《公路桥梁抗风设计规范》，顺风向和竖向分别以Kaimal谱[17]和Panofsky谱[18]为目标谱，脉动风速的空间相关性采用Davenport相干函数模拟[2]。在进行风谱模拟和相关函数的计算时，主要参数如下：主梁模拟点数nB取28，衰减因子λ取7，截止频率ωu取4π，频率分段数N取1 024，样本时距Δt取0.25 s，选用时段长30 min。取桥址区100年重现期的设计基准风速作为模拟风速，即V10为27.1 m/s，风速沿高度分布采用指数形式变化规律。总计生成50个模拟风场样本，通过时间总体平均，获得模拟风速时程的自谱和自相关函数，并与相对应的目标谱和目标相关函数进行比较，如图4和图5所示。

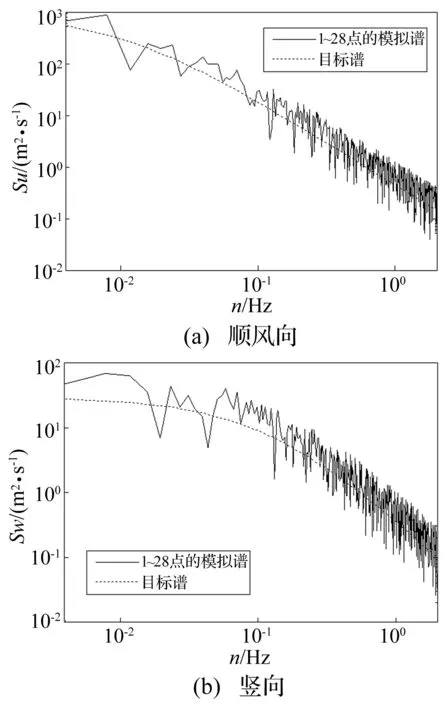
图4　主梁模拟谱与目标谱对比Fig.4 Comparison of power spectra of the girder

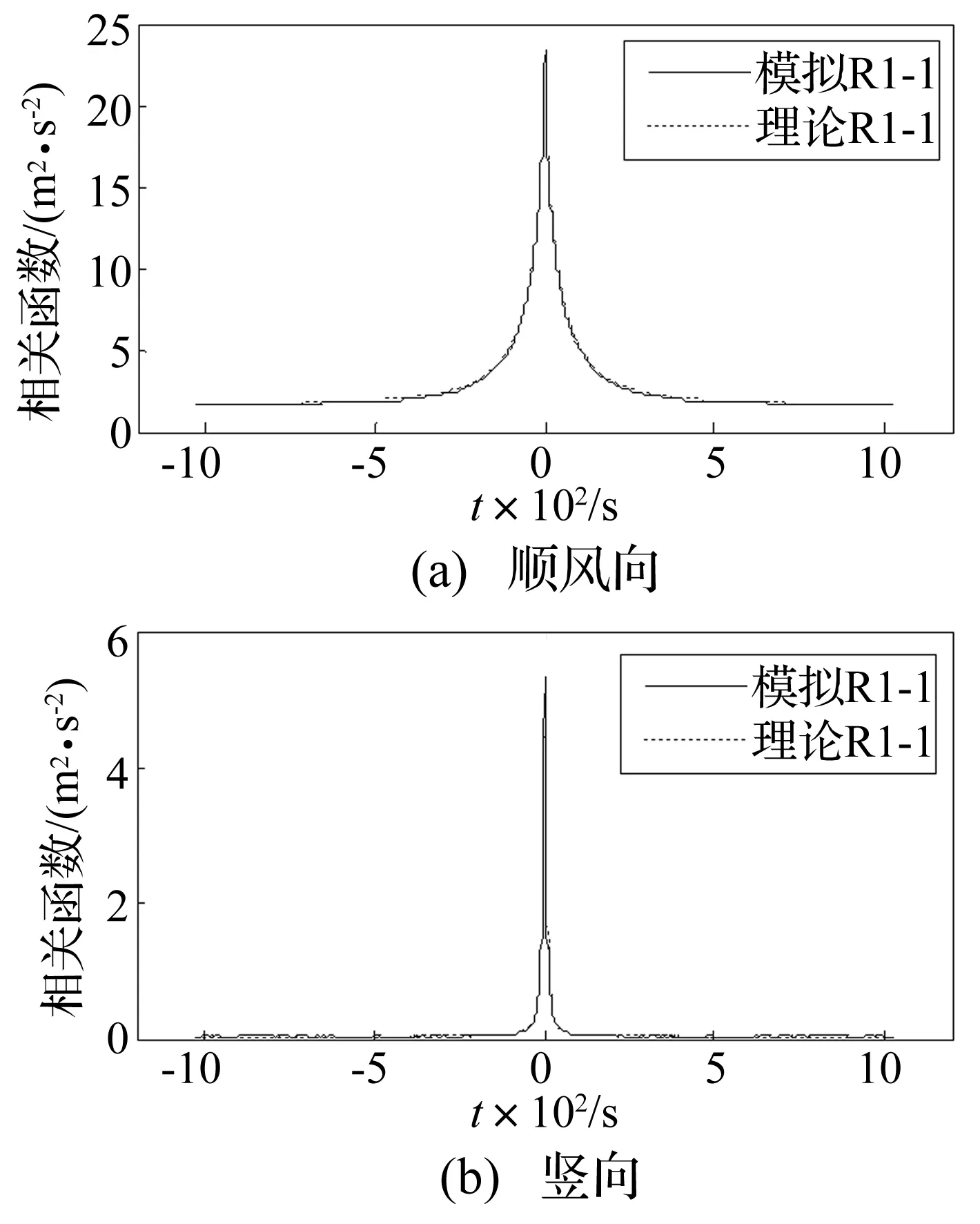
图5　主梁自相关函数对比Fig.5 Comparison of autocorrelation function of the main girder

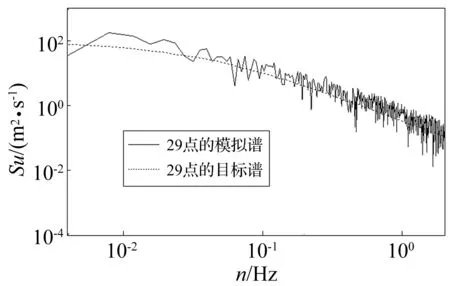
图6　中塔模拟自谱与目标谱对比Fig.6 Comparison of power spectra of the mid-tower

图4和图5表明，主梁模拟谱和目标谱以及自相关函数的模拟值与理论值的吻合程度均较高，从而验证了该桥三维脉动风场模拟方法的准确性。

3.3主塔风场模拟

由表1可知，本文仅考虑横桥向脉动风场对主塔的作用。为此，以Kaimal谱为目标谱进行风场模拟，其他参数与主梁风场模拟一致，共生成了50个风场样本。图6和图7分别给出了中塔顺风向脉动风功率谱以及相关函数模拟值与目标值的对比情况。由图可知，模拟风速时程的功率谱及相关函数均与理论值均吻合较好，进一步验证了本文风场模拟方法的有效性和可靠性。

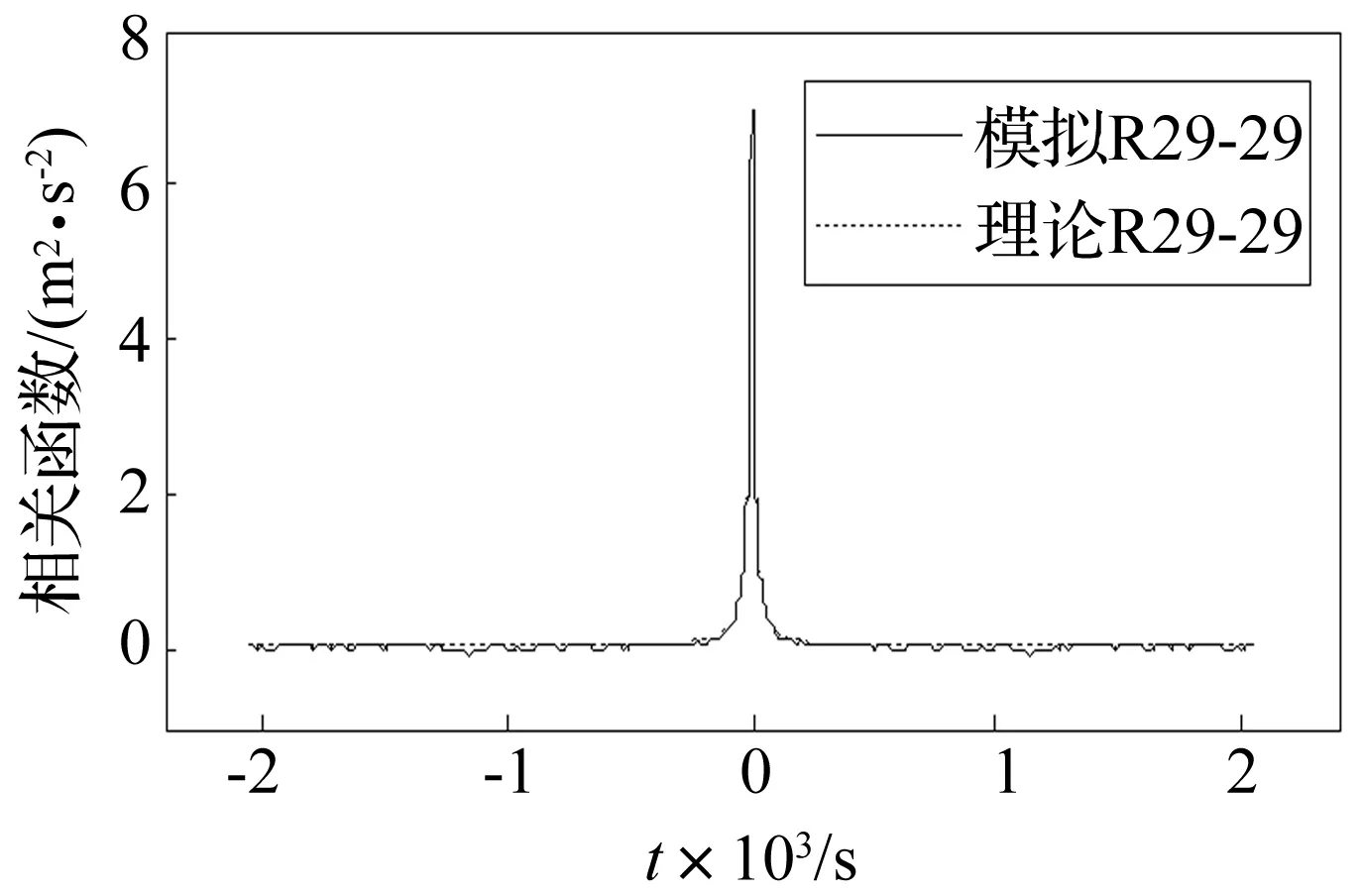
图7　中塔自相关函数对比Fig.7 Comparison ofautocorrelation function of the mid-tower

4空间相关系数对三塔悬索桥抖振响应的影响

无量纲衰减因子λ是描述脉动风速空间相关特性的重要参数，对实际的桥梁结构而言，λ的取值存在较大的不确定性。已有研究常根据实测和经验采用不同的λ值，如文献[13]对大气边界层风速的竖向空间相关性进行了研究，其中根据实测结果将顺风向λ取为10.2，横风向λ取为4.34；文献[12]在研究钢桁架悬索桥抖振响应与脉动风速空间相关性系数的关系时，分别取为5，7，9；文献[19]在进行苏通大桥主塔风速模拟时，参考桥址区多次台风实测值将λ取为10。总体而言，对大跨度桥梁脉动风场的空间相关特性的研究尚未深入。因此，将λ分别取7、10、15以及20，以研究空间相关系数对大跨度三塔悬索桥抖振响应的影响规律。

4.1基于ANSYS的大跨度三塔悬索桥抖振时程响应时程分析

在三维脉动风场模拟的基础上，利用ANSYS的瞬态动力学分析功能，对泰州大桥进行了抖振响应非线性时域分析，得到了大桥主梁各模拟点竖向、横向以及扭转抖振位移响应，其中λ=7时该桥主梁跨中各向位移响应如图8所示。时域分析中，采用Matrix27矩阵单元模拟主梁气动自激力，主梁断面的气动力系数和颤振导数均通过同济大学土木工程防灾国家重点实验室的同行们所进行的风洞试验获得[19]。

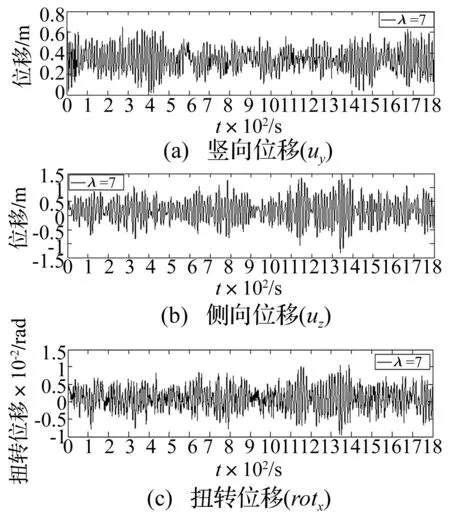
图8　不同紊流相关系数下主梁跨中抖振位移响应时程图Fig.8 Time-history of buffeting displacements response at the mid-span of girder with different turbulence correlation coefficients

4.2紊流空间相关系数的影响

基于快速傅里叶变换(FFT)技术对主梁跨中竖向、横向以及扭转抖振位移时程进行了功率谱分析，比较了无量纲衰减因子λ不同取值时的功率谱密度函数，对比结果如图9所示。同时对大桥主梁沿跨度方向各模拟点抖振位移响应RMS值进行统计，并针对不同相关系数下RMS值进行对比，对比结果如图10所示。

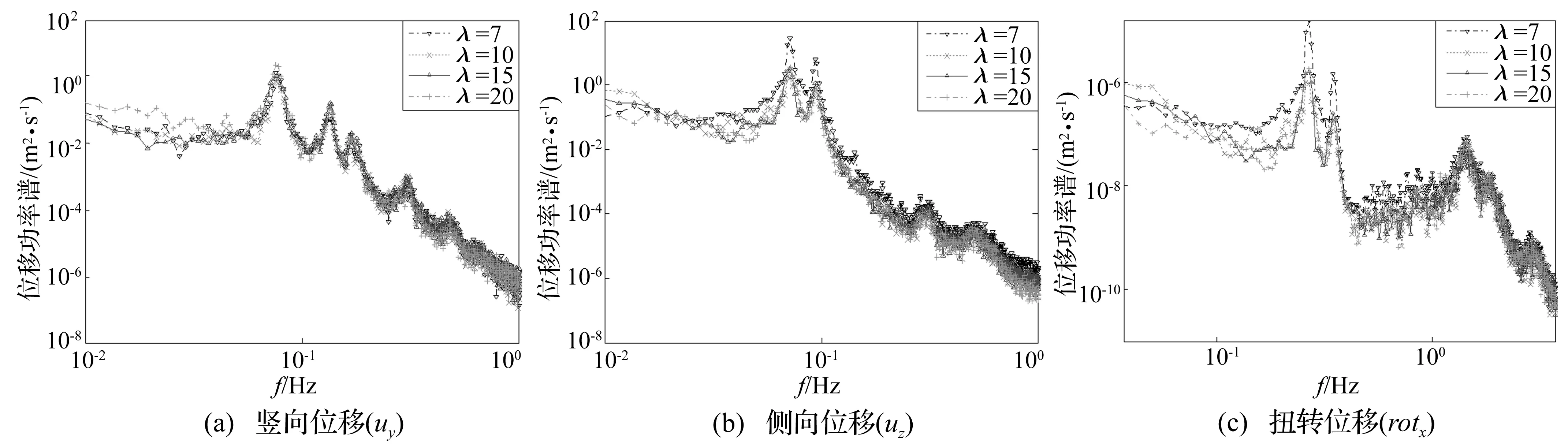
图9　不同紊流相关系数下主梁跨中抖振位移响应的功率谱密度比较Fig.9 Comparison of the PSDs of buffeting displacement at the mid-span of girder with different turbulence correlation coefficients

由图9可知，不同的紊流空间相关系数下，各方向位移功率谱整体趋势及峰值出现位置基本一致，但在λ=7时，竖向位移响应的功率谱整体低于其他取值情况，且λ取值越大，竖向位移响应功率谱越高；侧向位移和扭转位移的功率谱值在λ=7时均高于其他取值情况，且随着λ的取值增大，侧向位移和扭转位移响应的功率谱值逐渐降低。同时，由图9中各方向位移功率谱第一个峰值对应的频率可知，该桥主梁的竖向抖振响应主要由结构第一阶反对称竖弯振型控制，侧向抖振主要由结构第一阶反对称侧弯振型控制，扭转抖振响应主要由结构第一阶反对称扭转振型控制。主梁各方向的抖振响应主要由第一阶振型控制，高阶振型参与效应较小。

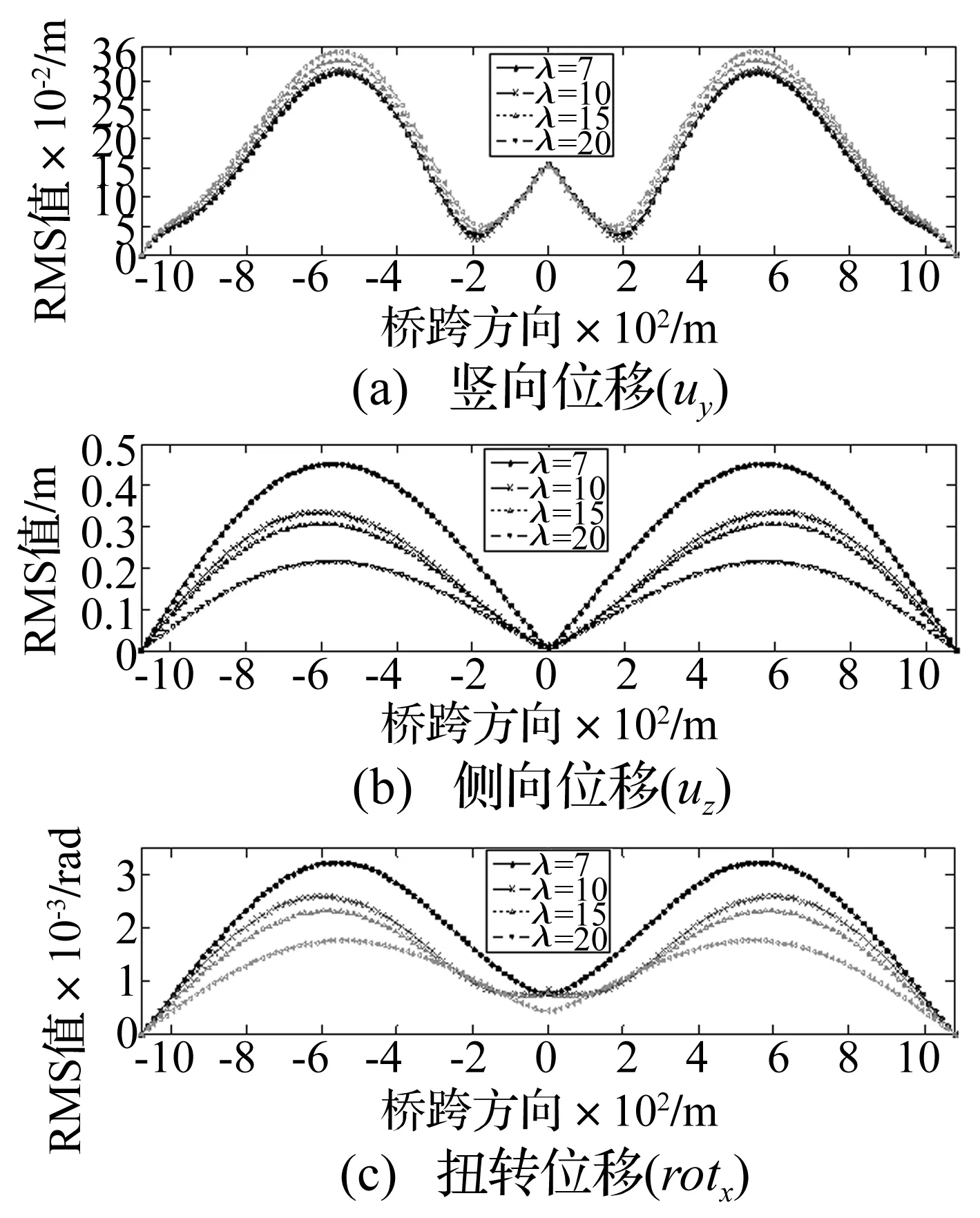
图10　不同紊流相关系数下主梁沿跨度方向各点抖振位移响应RMS值分布图Fig.10 RMS value distribution of buffeting displacement of girder along the span with different turbulence correlation coefficients

由图10可知，采用不同的紊流空间相关系数时，桥梁结构的抖振响应差异比较明显：其中竖向位移抖振响应RMS值随着空间相关系数的增大而略有增大，侧向位移与扭转位移的响应RMS值随着紊流相关系数的增大而减小。其中竖向位移的影响规律与现有研究结果有所出入[12]，可能与三塔悬索桥的结构形式和动力特性相关。该大跨度三塔悬索桥的一阶竖弯振型为反对称竖弯，而传统两塔悬索桥的一阶竖弯振型为正对称竖弯，这点值得引起注意。当紊流相关系数按照7、10、15、20依次变化时，主梁跨中竖向位移、侧向位移与扭转位移的RMS值分别为0.314 5 m、0.319 6 m、0.335 2 m、0.350 7 m；0.453 0 m、0.334 9 m、0.307 5 m、0.215 6 m；3.238 5×10-3、2.590 8×10-3、2.327 3×10-3、1.754 8×10-3。将λ=20与λ=7的结果相比，各方向差别分别为11.51%、-52.41%与-45.81%，以上数据表明，紊流空间相关系数对大跨度三塔悬索桥的抖振响应影响较大，要获得桥梁抖振响应的可靠值，就必须采用准确的紊流相关系数。

5结论

(1) 不同紊流空间相关系数下，主梁跨中抖振位移响应功率谱变化的整体趋势及峰值出现位置基本吻合。随着空间相关系数λ的增大，侧向位移和扭转位移响应的功率谱值逐渐降低，但竖向位移响应的功率谱略有增大，这点值得引起关注。

(2) 泰州大桥主梁的竖向抖振响应主要由结构第一阶反对称竖弯振型控制，侧向抖振主要由结构第一阶反对称侧弯振型控制，扭转抖振响应主要由结构第一阶反对称扭转振型控制。主梁各方向的抖振响应主要由第一阶振型控制，高阶振型参与效应较小。

(3) 主梁跨中竖向位移抖振响应RMS值随着衰减因子的增大而增大，侧向位移与扭转位移的响应RMS值随着衰减因子的增大而减小。可以看出，λ=7时主梁跨中竖向位移RMS值出现略小于其他取值情况，因此笼统地认为λ=7偏于保守的说法有待商榷。

(4) 紊流风的空间相关系数对大跨度桥梁的抖振响应影响显著，就本次算例而言，不同的衰减因子λ的取值所造成的大桥关键部位抖振响应计算差值可达50%以上，因此要精确分析大跨度桥梁的抖振响应，就必须采用准确的衰减因子。

参 考 文 献

[1] 伊藤学, 川田忠树. 超长大桥梁建设序幕——技术者的新挑战[M]. 刘健新, 和丕壮,译. 北京: 人民交通出版社, 2002.

[2] Simiu E, Scanlan R H. Wind effects on structures [M]. New York: JohnWiley & Sons, INC, 1996.

[3] Scanlan R H. The action of flexible bridge under wind Part 2: Buffeting theory [J]. Journal of Sound and Vibration, 1978, 160(2): 201-211.

[4] 项海帆. 现代桥梁抗风理论与实践[M]. 北京: 人民交通出版社, 2005.

[5] 陈政清. 桥梁风工程[M]. 北京: 人民交通出版社, 2005.

[6] 李永乐, 周述华, 强士中. 大跨度斜拉桥三维脉动风场模拟[J]. 土木工程学报, 2003, 36(10): 60-65.

LI Yong-le, ZHOU Shu-hua, QIANG Shi-zhong. Simulation of three-dimensional fluctuating wind field for large span cable-stayed bridge[J]. China Civil Engineering Journal, 2003, 36(10): 60-65.

[7] 曹映泓, 项海帆, 周颖. 大跨度桥梁随机风场的模拟[J]. 土木工程学报, 1998, 31(3): 72-79.

CAO Ying-hong, XIANG Hai-fan, ZHOU Ying. Simulation of stochastic wind field on long-span bridge [J]. China Civil Engineering Journal, 1998, 31(3): 72-79.

[8] 阎启, 李杰. 随机风场空间相干性研究[J]. 同济大学学报:自然科学版, 2011, 39(3): 333-339.

YAN Qi, LI Jie. Research on spatial coherence of stochastic wind field [J]. Journal of Tongji University:Natural Science, 2011, 39(3): 333-339.

[9] Larose G L. The dynamic action gusty winds on long-span bridge [M]. Copenhagen:Technical University of Denmark, 1997.

[10] 许志豪. 紊流风对大跨度分体双箱梁桥梁的作用[D]. 上海:同济大学, 2006.

[11] 黄东梅, 朱乐东, 丁泉顺. 大气边界层风速竖向相干函数实验研究[J]. 实验流体力学, 2009, 23(4): 34-40.

HUANG Dong-mei, ZHU Le-dong, DING Quan-shun. Experimental research on vertical coherence function of wind velocities in atmospheric boundary layer wind field [J]. Journal of Experiments in Fluid Mechanics, 2009, 23(4): 34-40.

[12] 于永帅, 钢桁架悬索桥抖振响应及其影响参数分析[D]. 湖南: 湖南大学, 2011.

[13] Song Li-li, Pang Jia-bin, Jiang Cheng-lin, et al. Field measurement and analysis of turbulence coherence for Typhoon Nuri at Macao Friendship Bridge [J]. Science China Technological Sciences, 2010, 53(10): 2647-2657.

[14] Toriumi R, Katsuchi H, Furuya N. A study on spatial correlation of natural wind [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2000, 87(2000): 203-216.

[15] Wang Hao, Zou Ke-guan, Li Ai-qun, et al. Parameter effects on the dynamic characteristics of a super-long-span triple-tower suspension bridge [J]. Journal of Zhejiang University Science A, 2010, 11(5):305-316.

[16] Shinozuka M, Jan C M. Digital simulation of random processes and its application [J]. Journal of Sound and Vibration, 1972, 25(1): 111-128.

[17] Kaimal J C. Spectral characteristics of surface layer turbulence [J]. Journal of the Royal Meteorological Society, 1972, 98(1): 563-589.

[18] Panofsky H A. McCormick R A. The spectrum of vertical velocity near the surface [J]. Journal of the Royal Meteorological Society, 1960, 86(370): 546-564.

[19] 王浩, 李爱群, 焦常科, 等. 基于规范及实测风谱的苏通大桥抖振响应对比研究[J]. 土木工程学报,2011,44(10):91-97.

WANG Hao, LI Ai-qun, JIAO Chang-ke, et al. Comparable study of the buffeting response of Sutong Bridge based on specification and measured wind power spectrum [J]. China Civil Engineering Journal, 2011, 44(10): 91-97.

Effects of the turbulent spatial correlation coefficient on buffeting responses of a triple-tower suspension bridge

MAO Jian-xiao, WANG Hao, TAO Tian-you, XU Zi-dong, LI Ai-qun

(Key Laboratory of Concrete and Prestressed Concrete Structures of Ministry of Education, Southeast University, Nanjing 210096, China)

Abstract:In order to obtain the accurate spatial correlation coefficients of turbulent flow and to investigate its effect on buffeting responses of bridge, the Taizhou Yangtze River Highway Bridge was taken as a reasearch example. The three-dimensional fluctuating wind field of the bridge was simulated with the harmonic synthetic method. And the nonlinear buffeting analysis on the bridge was conducted in time domain based on the ANSYS. In the research the dimensionless decay factor λ of Davenport correlation function was set as the control parameter and the influence of the spatial correlation coefficient of fluctuating wind on wind-induced buffeting responses of the long-span triple-tower suspension bridge was analysed. The results show that the spatial correlation coefficient of fluctuating wind has great influence on the wind-induced buffeting responses of bridge. The lateral and torsional buffeting displacements at the mid-span decrease with the augment of the decay factor, while the vertical one increases only slightly when the decay factor turns larger. The difference of buffeting responses caused by various decay factors could reach 50%. The results can provide references to the wind-induced buffeting analysis of long-span triple-tower suspension bridges.

Key words:triple-tower suspension bridges; turbulence spatial correlation coefficient; buffeting response; wind field simulation; correlation function

基金项目：国家973计划青年科学家专题(2015CB060000)；国家自然科学基金项目(51378111)；教育部新世纪优秀人才支持计划资助项目(NCET-13-0128)；霍英东青年教师应用研究项目(142007)；同济大学桥梁结构抗风技术交通行业重点实验室开放课题资助项目(KLWRTBMC12-02)

收稿日期：2015-02-26修改稿收到日期：2015-04-05

通信作者王浩 男，博士，研究员，博士生导师，1980年9月生

中图分类号:U448

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.10.032

第一作者 茅建校 男，博士生，1990年11月生

E-mail: wanghao1980@seu.edu.cn