电压跌落对风力机叶片振动影响分析

尹尧杰， 廖明夫， 吕　品， 刘展翅, 王四季

(西北工业大学 动力与能源学院，西安　710029)

电压跌落对风力机叶片振动影响分析

尹尧杰， 廖明夫， 吕品， 刘展翅, 王四季

(西北工业大学 动力与能源学院，西安710029)

摘要：风力机单机容量不断增大，装机容量不断增长，风力机与电网之间的耦合效应越发突出。电网的干扰以及故障会对风力机机械部件产生冲击。为了获得叶片在电网电压跌落时的动态响应，把叶片简化为悬臂梁，用3D Timoshenko梁进行离散化建模，建立了叶片运动的动力学方程，基于某1.5 MW风力机低电压穿越测试得到的转速，变桨曲线，获得叶片所受时变载荷的基础上，运用Newmark法对叶片在电压三相对称跌落与不对称跌落下的动态响应进行了计算。结果表明电压的跌落会对叶片产生冲击效应，在叶片拍打方向振动幅值比挥舞方向更大。叶片振动变化的总体特征随着风机载荷和电压跌落的幅值增大而增大的。同等工况和跌落幅度下，三相对称跌落时振动的变化要大于不对称跌落的振动变化。

关键词：电压跌落;风力机;叶片;Timoshenko梁模型;动态响应

随着风力发电技术快速发展，风力机单机容量不断增大，风电装机容量高速增长，风能已经成为重要的能源供应选择[1]。

图1　风力机与电网之间的耦合[3]Fig.1 Interaction between wind turbine and grid

过去风力机的设计要求主要关注风力机自身的安全性能，并没有考虑其对电网的影响[2]。然而，随着风力机装机容量的大规模增加，风力机与电网的耦合性增强，如图1所示，风力机的动态特性影响并网电能质量，而电网的干扰以及故障也会对风力机电气部件以及机械构件产生影响。

许多国家修订与更新了风力机并网要求[4]，其中的一个重要方面就是要求风力机具备低电压穿越能力，即当电网故障或扰动引起风电场并网点电压跌落时，在一定的电压跌落范围内，风电机组能够不间断并网运行[5]。如图2所示为中国国家电网对风力机低电压穿越的要求，曲线上方区域的跌落不允许风机脱网。

图2　风力机低电压穿越要求[6]Fig.2 Wind turbine LVRT requirements

低电压穿越能力在风力机的设计标准中也有体现。例如IEC 61400-1在风电场外部电网条件评估中规定为保证电气设计条件的兼容性，外部电网条件中要考虑当地电网对低电压穿越特性的要求[7]。

电网电压跌落引发风力机机械、电气功率的不平衡，使得机组载荷发生振荡，严重时导致机组切除。电压跌落导致风力发电机组脱网的原因不仅与电气部件有关，也可能与机械振动或附属系统的低电压承受能力有关。因此在风力发电机组进行低电压测试时，也要进行风电机组载荷相关测试[8]。在风力机的设计中需要评估电压跌落对风机各个部件动力学的影响。

双馈风力发电系统如图3所示作为一种主流机型采用齿轮箱升速，通过控制转子励磁电流的频率，使定子频率恒定，实现变速恒频发电[9]。双馈风机定子侧直接联接电网，这种直接耦合使得电网电压跌落直接反应在电机定子端电压上，使得其对电网故障比较敏感，双馈风力发电系统的低电压穿越特性也成为了研究热点。

图3　双馈风力发电系统Fig.3 Double-fed wind power generation system

风力机主要结构部件中，叶片是个展向长，弦向短的柔性体，很容易发生振动与变形[10-11]。叶片结构的变形和振动，不仅会对叶片自身的气动性能产生影响，也会对风机电能质量产生影响。

因此本文建立了3D Timoshenko梁的风力机叶片有限元模型，基于在某风场对某型1.5 MW双馈风力发电机组低电压穿越特性的测试数据[12]，计算与分析了对称电压跌落与不对称电压跌落对风力机叶片动态特性的影响。

1风力机叶片建模

1.1风力机坐标系统

图4　叶片坐标系Fig.4 Coordinate of the blade

本文采用德国GL[13]认证所定义的坐标系作为叶片计算的坐标系，整个坐标系统如图4所示，其中ZR沿叶片展长方向，XR垂直于ZR指向塔架方向，YR由右手规则确定，垂直于机舱主轴。

1.2叶片有限元模型

叶片展弦比很大，可以将叶片简化为悬臂梁[14]，大型风力机的叶片越来越长，柔性增强，空腹特性突出，使得剪切变形不能忽略，因此采用考虑剪切变形的2节点3D Timoshenko梁单元进行离散化，离散化后的叶片如图5所示。每个单元有2个节点，每个节点有6个自由度(3个位移，3个转角)。

图5　叶片离散化简图Fig.5 Discretization of the blade

1.3梁单元的刚度矩阵与质量矩阵

叶片离散化后，需要建立梁单元的刚度矩阵与质量矩阵。考虑剪切变形影响时，梁的法向位移(挠度)可以表示为两部分的叠加。

ω=ωb+ωs

(1)

式中，ωb是弯曲变形的法向位移；ωs是剪切变形的法向位移。

(2)

式中，Nb为Hermite插值函数；Ns为拉格朗日插值函数。

将式(2)代入梁弯曲最小势能原理的泛函式(3)

(3)

从δΠ=0可推导出Timoshenko梁的刚度矩阵[15]，具体表达形式见附录。

(4)

质量矩阵可以根据Hamilton原理推导，考虑梁的平移与旋转具体推导过程可参考文献[16]。

平移质量矩阵：

(5)

旋转质量矩阵：

(6)

式中，l为单元长度；ρ为材料密度；A为截面面积；Ir为回转半径；Nv,Nθ为插值形函数；ξ为无量纲局部坐标。

单元刚度矩阵为：

M=[Mt]e+[Mr]e

(7)

单元质量矩阵为对称矩阵，具体表达形式见附录。

(8)

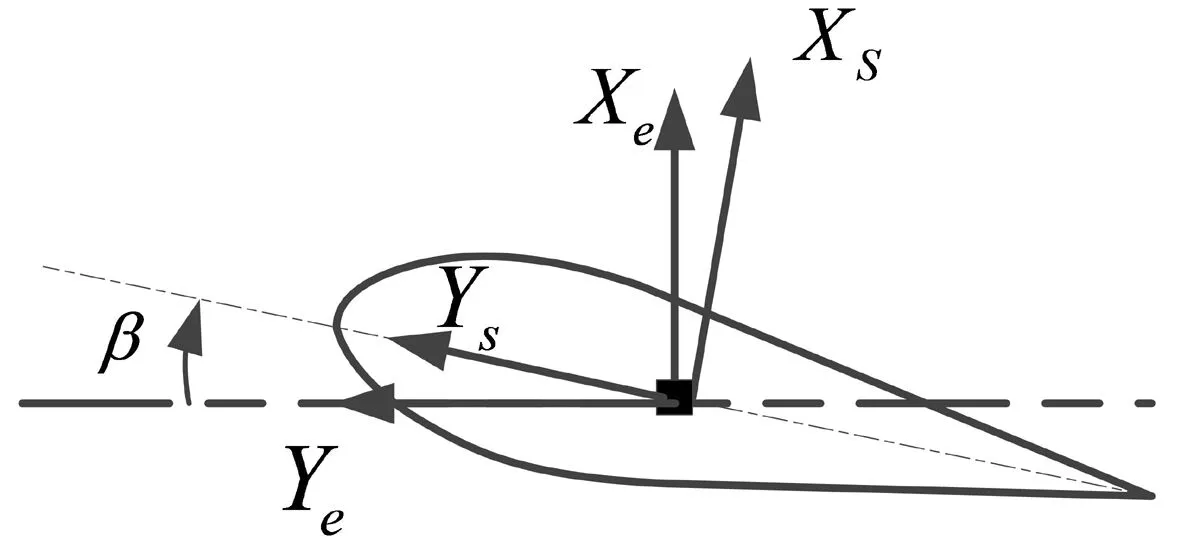
图6　叶片截面图Fig.6 Section of the blade

叶片抗弯刚度一般按截面主惯性轴(Xe-Ye)给出，需要分解到总体坐标系(Xs-Ys)上如图6所示，公式按式(9)给出[17]。

EIx=EIyecos2β-EIxesin2β

EIy=EIyesin2β+EIxecos2β

(9)

式中：Ixe,Iye为主惯性轴上的截面惯性矩；β为叶片截面扭角；E为材料弹性模量。

叶片旋转过程中产生的离心力会影响结构的刚度，产生离心刚化作用，影响叶片结构动力特性。离心刚化作用产生的单元应力刚度矩阵[18]为：

(10)

式中：

(11)

(12)

(13)

式中：F为作用于单元的轴向力；L为单元长度；Jz为极惯性矩。

将刚度矩阵与单元应力刚度矩阵相加得到单元组合刚度矩阵即：

Ke=K+Kσ

(14)

2叶片运动方程

组装单元的刚度矩阵与质量矩阵可以得到叶片整体的刚度矩阵与质量矩阵。根据最小势能原理可有导出叶片在时变载荷下的动力学运动方程为：

(15)

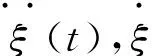
2.1空气动力学载荷

风力机气动性能计算方法采用叶素动量方法(BEM)，它综合了动量理论和叶素理论，考虑了叶尖损失、叶栅效应、失速修正、间隙修正及偏航角等因数的影响，可以比较精确地计算风轮转子的气动性能，所以在风力机设计和气动计算中得到广泛的应用。另外，还考虑了风剪、偏航、风轮的结构参数和风力机安装参数等[19]。在动态工况下，必须考虑动态入流与动态失速的影响对动量叶素-理论进行修正，具体的求解方法请参考文献[20]。如图7所示，叶片半径r的位置，来流风速为U∞，叶片旋转角速度为Ωr。轴向和切向诱导因子分别为a，a′。气流轴向速度为U∞(1-a)，气流的切向速度Ωr(1+a′)，合成的相对速度为W，由于风速方向的改变，将导致攻角α改变，定义来流角φ=α+β，β为安装角和截面扭角之和。L和D是叶素的升力和阻力。

图7　叶片的气动力Fig.7 Aerodynamic loads of the blade

应用叶素动量理论，考虑叶尖与轮毂损失F，速度诱导因子求解公式为[21]，

如果a≤ac时，

(16)

如果a>ac时

(17)

式中，ac≈0.2

F为损失因子，表达式为，

(18)

σ为实度系数，表达式为，

(19)

式中，c为翼型弦长。

Cn为法向力系数，表达式为，

Cn=CLcosφ+Cdsinφ

(20)

式中，CL,Cd为截面升力系数与阻力系数。

(21)

经过迭代可以求得叶素轴向与切向诱导因子。根据叶素-动量理论，单位长度的叶片在推力方向(X)与切向方向(Y)的力为:

(22)

式中：CL,Cd为截面升力系数与阻力系数；W为气流相对速度；φ为截面入流角；ρ为空气密度；c为翼型弦长。

2.2重力载荷

叶片旋转中，始终受到重力的作用，

重力在三个方向的分量表达式为：

(23)

2.3离心力载荷

叶片旋转过程中产生的离心力沿叶片展向向外，离心力的表达式可以表示为：

(24)

式中，ω为叶片旋转角速度。

根据求解得到的空气动力学载荷、重力载荷、离心力载荷可以得到单位长度叶片所受的载荷，

(25)

3叶片固有属性计算

采用建立的有限元模型对某1.5 MW的叶片动态特性进行计算，叶片R=35 m，其中轮毂半径Rhub=1.75 m。计算得到的自振频率与NREL软件BModes[22]进行对比如表1所示，可以看出对于叶片常关注的前几阶自振频率计算的误差很小,验证所建的Timoshenko梁模型的正确性。

表1　计算自振频率与BModes对比

4叶片的动态响应

中国电科院在其低电压穿越能力测试规程[23]规定，当风力发电有功功率输出分别在以下范围内时，测试风力发电机组在电网电压跌落时的响应特性：① 大功率输出0.9Pn之上;② 小功率输出0.1Pn到0.3Pn之间。响应测试内容既包括电压，有功功率，无功功率，电压，电流等电学参数，还需要测试风力机的运行参数，例如转速，变桨角的时间序列。规定的测试电网电压跌落规格如表2所示。

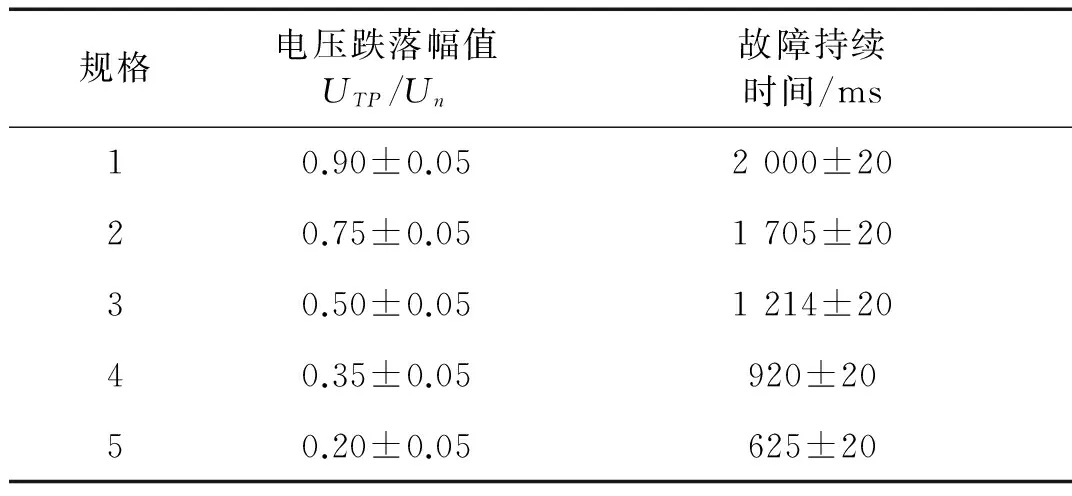
表2　电网电压跌落规格

对某型1.5 MW低电压穿越测试得到的转速与变桨响应曲线[12]，加载到所建立有叶片限元模型中，计算得到叶片所受的时变力，采用Newmark法积分可以得到叶片在低电压穿越时的动态响应。

由于振动的变化具有一定的规律性，因此在进行不同机组工况振动分析时，只对同一机组工况的两个极端电压跌落情况(最大跌落和最小跌落)进行对比分析，如表3所示。

表3　低电压穿越测试工况

4.1工况1与工况3对比分析

对比分析：工况1与工况3跌落幅值与跌落时间相同，只有机组的工况不同，工况1机组额定状态，工况3机组偏载状态。图8与图9可以看出，工况1机组工作在额定状态，电压的跌落引起了转速的波动，转速控制与变桨控制同时作用，而工况3机组工作在偏载状态，转速波动，并未变桨。

图10与图11可以看出平面外即叶片拍打方向振动的幅值比平面内即挥舞振动的幅值大。冲击的幅值即电压跌落时的振动到电压恢复时的振动，工况1在拍打方向是工况3的2倍，挥舞方向为1.5倍，跌落影响逐渐变小后，工况1中叶片的振动仍然为工况3的1.5倍左右。

4.2工况2与工况4的对比

对比分析：工况2与工况4跌落幅值与跌落时间相同，只有机组的工况不同，工况2机组额定状态，工况4机组偏载状态。图12与图13可以看出，工况2机组工作在额定状态，电压的跌落引起了转速的波动，转速控制与变桨控制同时作用，而工况4机组工作在偏载状态，转速波动，并未变桨。

图14和图15可以看出叶片的冲击效应很明显，叶片拍打方向的振动幅值比挥舞方向的振动大。冲击的幅值工况2在拍打方向是工况4的3.5倍，挥舞方向为4倍，跌落影响逐渐变小后，振动仍然为工况4的2倍。

4.3工况2与工况6的对比

对比分析：工况2与工况6机组工况，跌落时间相同，电压跌落的形式不同，工况2是电压对称跌落，工况6是不对称称跌落。从图12和图16可以看出两组工况电压的跌落使得转速控制与变桨控制同时作用。

从图17与图18可以看出，两组工况振动规律相似，都有明显的冲击现象，同样的叶片拍打方向的振动要比挥舞方向大。工况2比工况6在平面外方向的冲击幅值高出约12%，平面内方向高出约13%。

4.4工况1与工况2的对比

对比分析：工况1与工况2机组工况相同，电压跌落的幅值与跌落的时间不同。从图8和图12中可以看出，两组工况转速与变桨发生振荡。

从图19和图20可以看出， 冲击幅值在平面外方向工况2是工况1的1.8倍，平面内方向为2倍。

所有工况中工况2的电压跌落冲击效应最明显。图21，图22为叶尖振动的速度与加速度，可以看出振动变化很大。

图8　工况1的电压跌落曲线、转速与变桨角响应曲线Fig.8 Curve of voltage drop,speed and pich of test 1

图9　工况3的电压跌落曲线转速与变桨角响应曲线Fig.9 Curve of voltage drop,speed and pich of test 3

图10　叶尖平面外方向响应Fig.10 Dynamic response of blade tip in flap wise

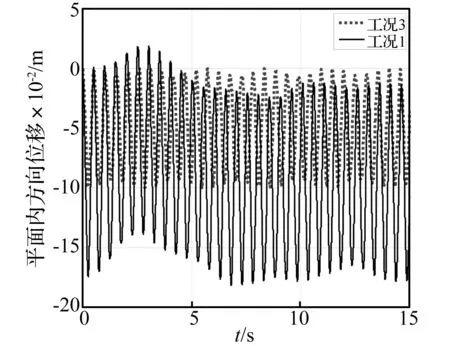
图11　叶尖平面内方向响应Fig.11 Dynamic response of blade tip in edgewise

4.5低穿过程中叶片振动的机理解释

当电网电压发生跌落时，发电机端的电磁转矩会瞬间变小，使得气动转矩与发电机转矩产生不平衡，叶轮转速增加，如果机组工作在偏载工况下，风力机组只有转速控制，如果机组工作在满载工况下，当转速瞬间发生较大的波动时，转速控制与变桨控制同时作用。

如上文叶片载荷分析，可知作用在叶片上的力，尤其是气动力与转速以及变桨角密切相关，并且是强烈的非线性关系，转速与变桨角波动，引起作用于叶片上的气动力发生波动，进而激起叶片发生振动。

另外从结构特性分析，当变桨角发生改变时候，叶片挥舞与拍打方向的刚度分布会发生改变，使得叶片的自振频率发生改变，如图23所示，也是引起叶片振动的原因。

图12　工况2的电压跌落曲线转速与变桨角响应曲线Fig.12 Curve of voltage drop,speed and pich of test 2

图13　工况4的电压跌落曲线转速与变桨角响应曲线Fig.13 Curve of voltage drop,speed and pich of test 2

图14　叶尖平面外方向响应Fig.14 Dynamic response of blade tip in flap wise

图15　叶尖平面内方向响应Fig.15 Dynamic response of blade tip in edgewise

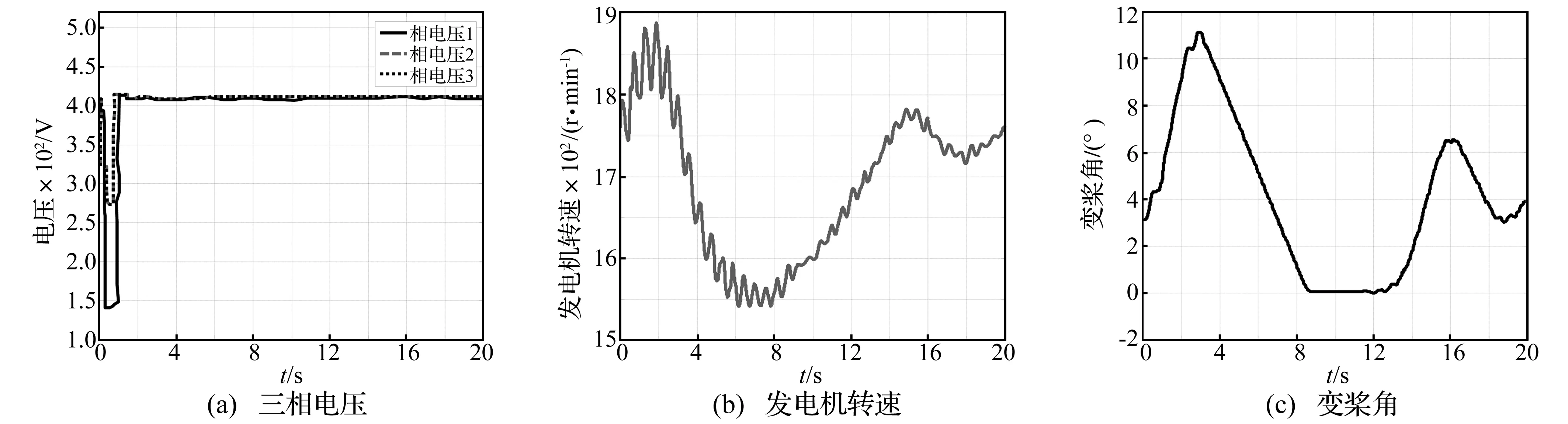
图16　工况6的电压跌落曲线 转速与变桨角响应曲线Fig.16 Curve of voltage drop,speed and pich of test 2

图17 叶尖平面外方向响应Fig.17Dynamicresponseofbladetipinflapwise图18 叶尖平面内方向响应Fig.18Dynamicresponseofbladetipinedgewise图19 叶尖平面外方向响应Fig.19Dynamicresponseofbladetipinflapwise

图20 叶尖平面内方向响应Fig.20Dynamicresponseofbladetipinedgewise图21 叶尖振动速度Fig.21Vibrationofbladetip图22 叶尖振动加速度Fig.22Vibrationaccelerationofthebladetip

图23　变桨角对叶片自振频率的影响Fig.23 The impact of pitch angle on the blade natural frequency

叶片的振动会与气动力形成耦合，使得叶片的振动超标引起机组的振动报警，影响机组的安全稳定运行。

5结论

通过以上的建模计算，结果的对比与分析可以得出以下结论：

(1) 风力机在低电压穿越过程中，由于载荷发生振荡，叶片的振动具有明显的冲击。其中叶片拍打方向振动幅值更明显，叶片拍打方向的载荷变化会引起风力机整机轴向载荷的变化，影响机组的安全稳定运行。

(2) 叶片振动变化的总体特征是随着电压跌落的幅值增大而增大的。同等工况下叶片的振动在电压跌落90%工况下，振动变化不是很明显，在电压跌落20%工况下，出现较大的冲击振动，其冲击振动是90%跌落的2倍。

(3) 叶片振动变化随着风机载荷的增大而增大。跌落90%时额定工况是偏载工况的2倍，跌落20%时额定工况是偏载工况的3.5倍.电压跌落影响逐渐消失，振动仍然是分别跌落前的1.5倍与2倍。

(4) 同等工况和跌落幅度下，三相对称跌落时振动的变化要比不对称跌落的振动大10%左右。

参 考 文 献

[1] Gasch R,Twele J.Windkraftanlagen: Grundlagen, Entwurf, Planung und Betrieb[M].Berlin：Springer Vieweg，2013.

[2] Fadaeinedjad R,Moschopoulos G,Moallem M.Investigation of voltage sag impact on wind turbine tower vibrations[J].Wind Energy,2008，11(4):351-375.

[3] Burton T,Jenkins N,Sharpe D,et al. Wind energy handbook[M].2nd ed.Chichester:John Wiley&Sons，2011.

[4] Hansen A D,Cutululis N A,Markou H,et al.Grid fault and design-basis for wind turbines—Final report[R]. Risφ-R-1714, Roskilde:RisφNational Laboratory for Sustainable Energy Technical University of Denmark，2010.

[5] 廖明夫,Gasch R,Twele J.风力发电技术[M].西安：西北工业大学出版社，2009.

[6] 国家电网公司风电场接入电网技术规定[S].北京：国家电网中国电力科学研究院，2009.

[7] IEC 61400-1.Wind turbine-part1:design requirements[S]. Geneva: International Electrotechnical Commission,2005.

[8] IEC-61400-21-2008. Part 21: Measurement and assessment of power quality characteristics of grid connected wind turbines[S]. Geneva: International Electrotechnical Commission,2008.

[9] Heier S.Grid integration of wind energy conversion systems[M]. 2nd ed. Chichester:John Wiley&Sons, 2006.

[10] 刘雄,李刚强,陈严,等.水平轴风力机叶片动态响应分析[J].机械工程学报，2010，46(12)：128-134.

LIU Xiong, LI Gang-qiang,CHEN Yan,et al. Dynamic response analysis of the blade of horizontal axis wind turbines[J]. Journal of Mechanical Engineering, 2010,46(12)：128-134.

[11] 黄巍.大型水平轴风力机整机动力学研究[D].西安：西北工业大学，2012.

[12] 廖明夫，金路，刘展翅.某1.5MW风力机低电压穿越测试报告[R].西安：旋转机械与风能装置测控研究所，2010.

[13] Guideline for the Certification of Wind Turbine [S].Hamburg:Germanischer Lioyd,2004.

[14] Gasch R,Twele J.Wind power plants—fundamental,design,construction and operation[M].Berlin:Solarpraxis AG,2002.

[15] 王勖成.有限单元法[M].北京：清华大学出版社，2003.

[16] Yokoyama T.Vibrations of a hanging Timoshenko beam under gravity[J].Journal of Sound and Vibration,1990,141(2):245-258.

[17] 李立本，宋宪耕，贺德馨，等.风力机结构动力学[M].北京：北京航空航天大学出版社，1999.

[18] 王新敏，李义强，许宏伟.ANSYS结构分析单元与应用[M].北京：人民交通出版社，2011.

[19] 金鑫,何玉林,刘桦,等.风力发电机耦合振动分析[J].振动与冲击，2007，26(8)：144-148.

JIN Xin，HE Yu-lin，LIU Hua，et al.Coupled vibration analysis of wind turbine[J].Journal of Vibration and Shock, 2007，26(8)：144-148.

[20] 董礼.水平轴变速变桨风力机气动设计与控制技术研究[D].西安：西北工业大学，2011.

[21] Hansen M O L.Aerodynamics of wind turbines[M].London:Earthscan,2008.

[22] Bir G S.User’s guide to bmodes[R].Golden:National Renewable Energy Laboratory,2007.

[23] NB/T 31051-2014. 风电机组低电压穿越能力测试规程[S].北京：中国电科院，2014.

附录：

刚度矩阵具体形式

其中：A为截面面积；E为弹性模量；L为单元长度；G为剪切模量；J为扭转惯性矩。

ay=a(Iy,φx)

ax=a(Ix,φy)

by,bx,cy,cx,dy,dx,ey,ex,fy,fx形式同ay,ax

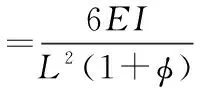
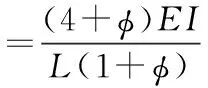
其中：

其中：Ix为x方向的截面惯性矩；Iy为y方向的截面惯性矩；kx为x方向的剪切系数；ky为y方向的剪切系数。

质量矩阵具体形式

其中：

Ay=A(ry,φx)

Ax=A(rx,φy)

By,Bx,Cy,Cx,Dy,Dx,Ey,Ex,Fy,Fx形式同Ay,Ax

其中：

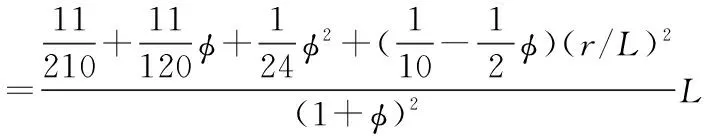
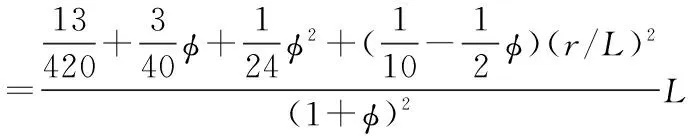
F(r,φ)=

其中：Jz为极惯性矩；rx为回转半径；ry为回转半径。

Investigation of voltage sag impact on wind turbine blade vibrations

YIN Yao-jie, LIAO Ming-fu, LÜ Pin, LIU Zhan-chi,WANG Si-ji

(School of Power and Energy, Northwestern Polytechnical University, Xi’an 710129, China)

Abstract:Recently the size and the capacity of wind turbines increase rapidly, the interactions between the wind turbines and the electric grid becomes more obvious. The disturbances from the grid and the faults of the grid will have impact on mechanical components of wind turbines. In order to obtain the dynamic responses of the blade under voltage sag, the blade was modeled as a cantilever and discretized by applying 3D Timoshenko beam element, considering the centrifugal stiffening of the rotating blade. The structural dynamic equation of the blade was established and the time-varying loads acting on the blade were calculated based on the data from a 1.5 MW wind turbine LVRT(low voltage ride through) test. The dynamic responses of the blade under the three-phase symmetrical voltage dip and three-phase asymmetry dip were calculated by applying Newmark method. The results show that, the voltage dip produces the transient loads and excites the vibrations of the blade. The amplitude of vibration in the flap wise is bigger than that in the edgewise. The vibration increases with the increase of the load of wind turbine and the magnitude of voltage drop. The dynamic responses of the blade under the three-phase symmetrical voltage dip are larger than those under three-phase asymmetry dip.

Key words:voltage sag; wind turbine; blade; Timoshenko beam ; dynamic response

基金项目：中央高校基本科研业务专项资金资助(310201513J(Ⅱ)CG015)

收稿日期：2015-07-28修改稿收到日期：2015-10-13

通信作者廖明夫 男，博士,教授，博士生导师，1960年2月生

中图分类号:TK83

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.10.031

第一作者 尹尧杰 男，博士生，1987年11月生