基于里兹法研究复合材料层合板的动力屈曲问题

李　楠 ， 韩志军 ， 路国运

(1. 太原理工大学 力学学院，太原　030024; 2. 太原理工大学 建筑与土木工程学院，太原　030024)

基于里兹法研究复合材料层合板的动力屈曲问题

李楠1， 韩志军1， 路国运2

(1. 太原理工大学 力学学院，太原030024; 2. 太原理工大学 建筑与土木工程学院，太原030024)

摘要：考虑应力波效应，引用棣莫弗公式与里兹法结合来研究复合材料板的动力屈曲问题。设板的试函数为含有时间项的三角函数形式，通过对试函数奇偶性的判断得出有效的动力屈曲解。应用棣莫弗公式对控制方程进行化简，通过对化简所得的微分方程解的讨论，得出了应力波反射前复合材料层合板的临界动力屈曲载荷表达式,并探讨了不同铺层角度对于临界动力屈曲的影响。将里兹法获得的屈曲载荷值曲线与分离变量法所得的曲线进行对比,两条曲线几乎完全重合，同时应用ABAQUS有限元软件对不同角度下复合材料层合板进行动力屈曲模拟，将临界屈曲载荷模拟值与里兹法得出的理论值进行对比，二者误差不超过百分之五，说明棣莫弗公式与里兹法结合可有效应用于复合材料板动力屈曲的研究。

关键词：棣莫弗公式；里兹法；应力波；临界动力屈曲载荷

复合材料层合板以其高比强度、高比刚度等诸多优点被广泛应用于航空、航天、军工、机械等领域，由于板结构在工作过程中存在动力载荷作用下的屈曲现象，如航天器翼板结构在升空中遭受的冲击载荷作用，军事目标物存在的炮弹冲击屈曲问题，因此针对复合材料板的动力屈曲研究已成为工程部件设计、研究的关键性问题[1-3]。Shariyat[4-6]在其一系列文章中提出了一种双叠加高阶global-local理论来研究有缺陷复合材料板、黏弹性复合材料板在热-力载荷作用下的动力屈曲与后屈曲问题。Czechowski等[7-8]研究了均匀温度载荷与动力轴向压力作用下复合材料功能梯度板的动力屈曲问题，研究假定材料特性在板厚范围内均匀变化且不依赖于温度的影响。秦建兵[9]在考虑应力波效应的前提下使用分离变量法求出了复合材料层合板的临界动力屈曲解，但只局限于对称屈曲的情况。张小波[10]采用有限元软件对正交各项异性蜂窝材料壁板的动力屈曲性能进行研究，讨论了冲击载荷类型、壁板几何尺寸、铺层等因素对动力屈曲的影响。

目前针对动力屈曲的求解方法有分离变量法[9, 11-12]、双特征参数法等。本文考虑应力波效应，将棣莫弗公式与里兹法结合来研究轴向阶跃载荷作用下的复合材料板的动力屈曲问题。设板的试函数为三角函数与时间项相乘的形式，通过函数奇偶性判断得出满足不同边界条件和波阵面约束条件的准确试验函数形式。基于棣莫弗公式对复合材料板的控制方程进行化简，得出了应力波反射前复合材料板临界动力屈曲载荷的表达式。应用MATLAB软件将本法与分离变量法所得的临界载荷值曲线进行对比，二者几乎完全重合。同时应用ABAQUS有限元软件对复合材料板的动力屈曲进行模拟，将本法得到的理论值与有限元模拟值进行对比，二者误差在允许范围内，可见棣莫弗公式与里兹法结合可有效应用于复合材料板动力屈曲的研究。

1复合材料板的控制方程

如图1所示，复合材料层合板在x=0,y=0以及y=b处为简支边界条件，在x=a处为固支边界条件，此类板简称为SFSS板；复合材料层合板在x=0处为夹支边界条件, 在y=0以及y=b处为简支边界条件，在x=a处为固支端边界条件，此类板简称为CFSS板。

图1　SFSS板、CFSS板加载示意图Fig.1 SFSS and CFSS plate under the axial step load

图1中轴向阶跃载荷作用于板的夹支或简支端，产生的应力波沿x方向在板中传播。应力波反射前，层合板中各段的单位轴力为：

(1)

复合材料层合板的本构方程为：

(2)

式中，Aij为拉伸刚度，Dij为弯曲刚度，Bij为弯曲拉伸耦合刚度

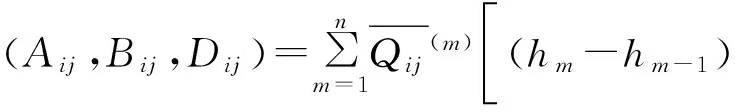
对于各向同性对称层合板、特殊正交各向异性对称层合板以及正规对称正交铺设层合板来说，刚度矩阵D16,D26,A16,A26都为0，而正规对称角铺设层合板的D16,D26,A16,A26相对较小计算中可简化[13-14]。这样考虑转动惯量不计轴向惯性，由Hamilton原理可以导出层合板的控制方程，进一步化简为:

D11wxxxx+(2D12+4D66)wxxyy+D22wyyyy+Nwxx+

(3)

2基于里兹法分析复合材料板的动力屈曲

2.1由函数奇偶性确定复合材料板动力屈曲解

由于里兹法研究动力屈曲的关键在于给出试函数的精确性，因此本文通过对试函数奇偶性的判定来得出有效准确的动力屈曲解。以CFSS板为例，假设应力波反射前复合材料板发生动力屈曲，设试函数即屈曲解为：

(4)

式中，n1,n2与m是屈曲模态阶数，A与B为相关待定系数。式(4)应满足CFSS板的边界条件与波阵面约束条件式(5)与(6)。

(5)

(6)

将式(4)代入式(5)中可得：

(7)

(8)

式中n1=m=(1,2,3…),n2=n1+2

同理可得复合材料SFSS板的屈曲试函数为：

(9)

式中，n1=m=(1,2,3…),n2=n1+1

2.2基于棣莫弗公式化简板控制方程

由棣莫弗公式(10)可以得出式(11)与(12)

(cosθ+isinθ)n+cos(nθ)+isin(nθ)

(10)

(11)

(12)

由式(11)可以得到

(13)

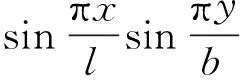
(14)

进一步化简式(14)可得微分方程：

(15)

其中

解该微分方程式(15)可知当(α-β)<0时方程解为指数形式，表明运动无界的系统呈现不稳定的状态。当(α-β)>0时系统围绕平衡位置做微小扰动，系统处于稳定平衡[11]。当(α-β)=0时为板屈曲临界状态，由此可导出应力波反射前复合材料CFSS板临界动力屈曲载荷表达式为：

(16)

式中，n1=m=(1,2,3…),n2=n1+2

同理可以求出应力波反射前复合材料SFSS板临界动力屈曲载荷表达式：

(17)

式中，n1=m=(1,2,3…),n2=n1+1

应用文献[9, 11-12]中分离变量法可以得出应力波反射前复合材料CFSS板与SFSS板临界动力屈曲载荷表达式：

(18)

其中CFSS板n1=m=(1,2,3…),n2=n1+2

SFSS板n1=m=(1,2,3…),n2=n1+1

3数值计算

本文应用MATLAB软件对里兹法与分离变量法所得结果进行对比。算例设定层合板长a=0.5 m,板宽b=0.3 m，板厚h=0.005 m,层厚t=0.001 m,材料选取碳环氧树脂复合材料，具体材料参数如下：

E1=139 GPa,E2=E3=9.4 GPa,μ23=0.33μ12=μ13=0.309 5,G12=G13=4.5 GPa,G23=2.98 GPa，ρ=1 583 kg/m3

图2与图3是分别用分离变量法和里兹法在MATLAB软件中得到的临界屈曲载荷与临界屈曲长度的关系曲线图。

图2　CFSS层合板临界屈曲载荷与屈曲长度的曲线图Fig.2 Relationship between the critical load and length of CFSS plates

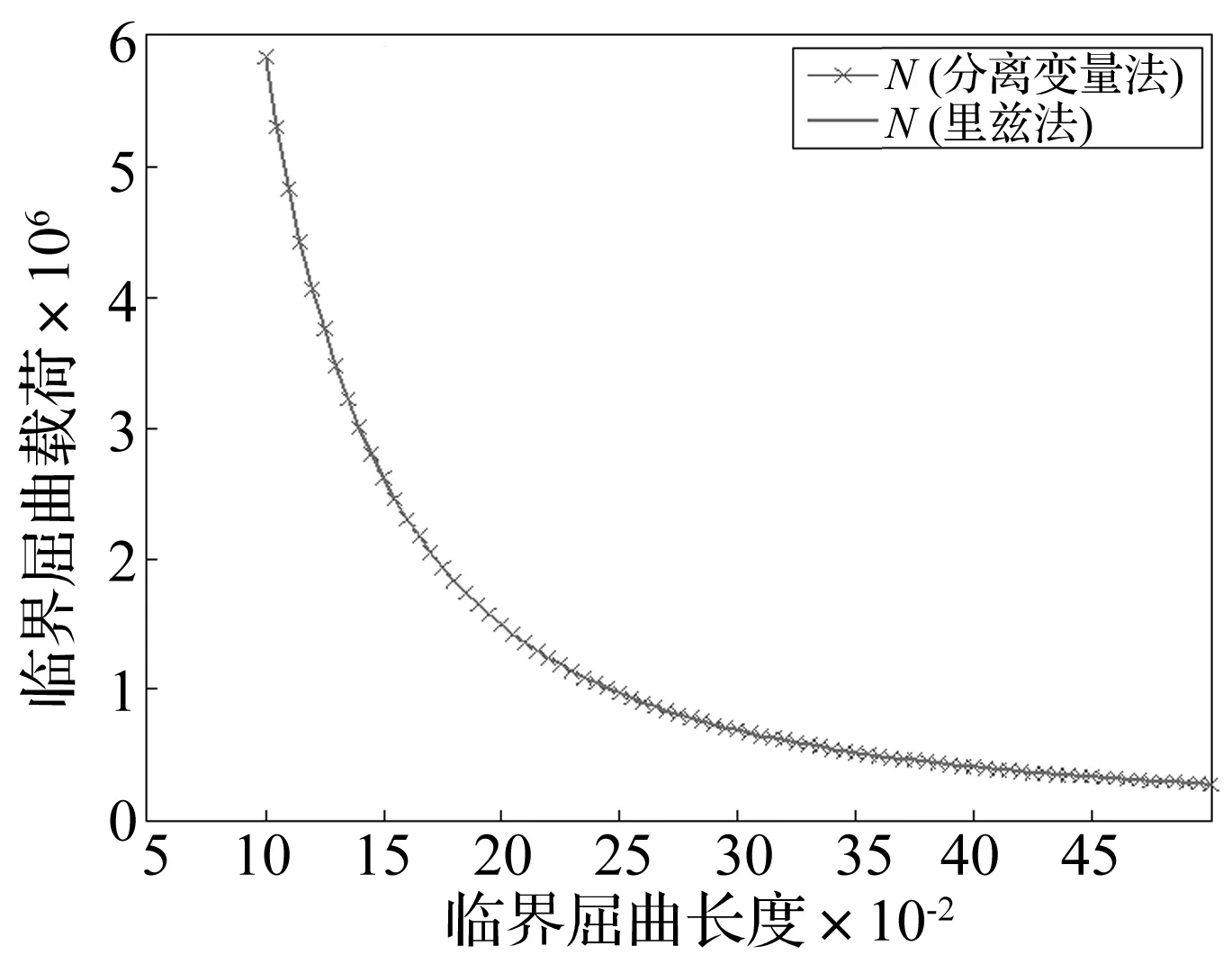
图3　SFSS层合板临界屈曲载荷与屈曲长度的曲线图Fig.3 Relationship between the critical load and length of SFSS plates

图2与图3表明，不论是SFSS板还是CFSS板，应用里兹法与分离变量法所得出的曲线图几乎完全重合。这表明在不考虑剪切效应的情况下，两种方法在动力屈曲的研究上具有同样的精度，在本文研究中式(18)多出的有关D22一项相比较前两项来说对结果的影响非常小可忽略。

图4是应力波反射前，不同铺层组的正规对称角铺设层合板的临界动力屈曲载荷值与临界屈曲长度的关系图线，层合板铺层组如图4所示。

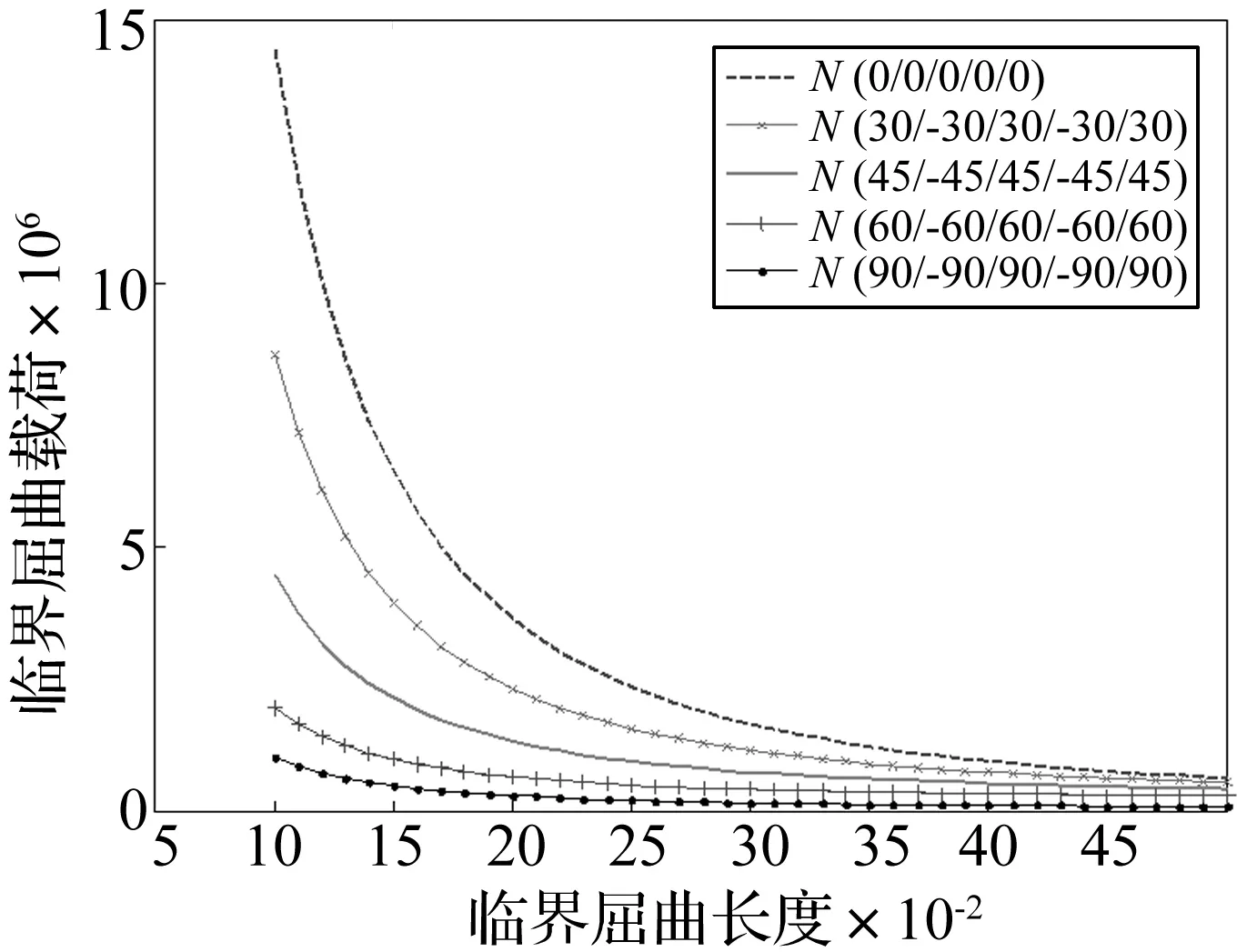
图4　不同铺层组合下临界屈曲载荷值与临界长度的关系图线Fig.4 Relationship between the critical load and length with different lay-up angle of composite laminated plates

图4表明正规对称角铺设层合板的临界动力屈曲载荷值随临界屈曲长度的增大而减小，在屈曲临界长度相同的情况下，临界载荷则随着铺层角度的增大而逐渐减小，并且这种减小趋势也随之呈现逐渐递减的趋势。

4有限元模拟

应用ABAQUS有限元软件模拟不同铺层角度下板的动力屈曲。模型采用ABAQUS/Explicit中的S4R有限元单元(见图5)，材料选用碳环氧树脂复合材料, 模拟中在板的夹支或者简支端作用阶跃载荷，使用幅值曲线使载荷在极短时间内达到幅值。应用ABAQUS后处理软件获得了板关键单元(对称)上下层应变时程曲线，当层合板未发生动力屈曲时，两条应变时程曲线始终重合；当板在一定载荷作用下发生动力屈曲时，层合板上下层关键单元的应变时程曲线将出现如图6所示的分叉现象，此时对应的时间(提取了上下层分叉曲线的数据，找出最先出现稳定分叉的时刻点)是临界动力屈曲时间，其载荷是临界动力屈曲载荷模拟值。将临界屈曲时间代入屈曲载荷表达式即可解得临界屈曲载荷的理论值。

图5　有限单元模型图Fig.5 The finite element model of laminated composite plates

图6　复合材料层合板动力屈曲分叉图Fig.6 The bifurcation of dynamic buckling on the laminated composite plate

表1是不同铺层角度下SFSS碳环氧树脂层合板的屈曲载荷理论值与模拟值的对比表。

表1　SFSS层合板临界屈曲载荷的理论值与模拟值对比

表1表明理论值与模拟值基本一致，其误差均未超过5%，在许可范围内。综合考虑表1、图2以及图3，表明采用里兹法与棣莫弗公式相结合来求解复合材料板的动力屈曲是可行的。

5结论

依据理论研究、MATLAB数值分析以及有限元模拟，本文得出以下结论：

(1) 考虑应力波效应，采用棣莫弗公式与里兹法结合的方法来研究复合材料板的动力屈曲，得出了应力波反射前复合材料层合板的动力屈曲临界载荷表达式。应用MTALAB软件将里兹法得出的临界屈曲载荷表达式的关系曲线与分离变量法得出的表达式的关系曲线进行对比，结果两条曲线几乎完全重合，说明新方法具有与分离变量法同等的精度。

(2) 应用MTALAB软件讨论了层合板不同铺层组对于屈曲临界载荷的影响，曲线图表明在临界屈曲长度相同的情况下，临界载荷则随着铺层角度的增大而逐渐减小，并且这种减小趋势也随之呈现逐渐递减的趋势。

(3) 应用ABAQUS有限元软件模拟不同铺层角度下复合材料板的动力屈曲。将临界动力屈曲载荷模拟结果与理论结果进行对比，误差均未超过百分之五，表明采用棣莫弗公式与里兹法结合的方法可以有效应用于复合材料板动力屈曲的研究。

参 考 文 献

[1] 唐文勇,张圣坤,陈铁云. 复合材料层合板条的流固耦合动力屈曲分析[J]. 上海交通大学学报, 2000,34(1):46-50.

TANG Wen-yong,ZHANG Sheng-kun, CHEN Tie-yun.Analysis of solid-fluid interaction dynamic buckling of a laminated composite strip[J]. Journal of Shanghai Jiaotong University, 2000,34(1):46-50.

[2] 彭诚洋. 船舶结构在流-固冲击作用下的动力屈曲[D].哈尔滨：哈尔滨工程大学，2005.

[3] 肖刚. 结构在约束下和动力作用下屈曲的数值模拟[D].上海：上海交通大学，2008.

[4] Shariyat M. Non-linear dynamic thermo-mechanical buckling analysis of the imperfect sandwich plates based on a generalized three-dimensional high-order global-local plate theory[J].Composite Structures, 2010,92(1):72-85.

[5] Shariyat M. A double-superposition global-local theory for vibration and dynamic buckling analyses of viscoelastic composite/sandwich plates: a complex modulus approach [J].Archive of Applied Mechanics, 2011,81(9):1253-1268.

[6] Shariyat M. A nonlinear double-superposition global-local theory for dynamic buckling of imperfect viscoelastic composite/sandwich plates: a hierarchical constitutive model [J]. Composite Structures, 2011,93(7):1890-1899.

[7] Czechowski L,Kowal-Michalska K. Static and dynamic buckling of rectangular functionally graded plates subjected to thermal loading [J]. Strength of Materials, 2013,45(6):666-673.

[8] Kowal-Michalska K,Mania R. Static and dynamic thermo-mechanical buckling loads of functionally graded plates [J]. Mechanics and Mechanical Engineering, 2013,17(1):99-112.

[9] 秦建兵. 复合材料层合板的屈曲及侵彻行为研究 [D]. 太原：太原理工大学, 2013.

[10] 张小波. 复合材料蜂窝结构面外静、动力屈曲研究[D].武汉：华中科技大学,2013.

[11] 韩志军. 直杆的撞击屈曲及其应力波效应的实验和理论研究[D].太原：太原理工大学, 2005.

[12] 康超. 轴向冲击复合材料杆的动力屈曲及静力作用下层合板屈曲研究[D].太原：太原理工大学, 2011.

[13] Reddy J N. Mechanics of laminated composite plates and shells: theory and analysis[M] . Boca Raton: CRC Press, 2004.

[14] 沈观林,胡更开. 复合材料力学[M].北京：清华大学出版社，2006.

Dynamic buckling analysis of laminated composite plates by using Ritz method

LI Nan1, HAN Zhi-jun1, LU Guo-yun2

(1. College of Mechanics, Taiyuan University of Technology, Taiyuan 030024, China;2. College of Architecture and Civil Engineering, Taiyuan University of Technology, Taiyuan 030024, China)

Abstract:Taking into account the effect of stress wave, the dynamic buckling of laminated composite plates under axial step loading was analysed theoretically by using Ritz method. The trigonometric function including time items was used as a trial function and the effective dynamic buckling solution was deduced by analyzing the parity of trial function. Based on the Abraham de Moivre’s formula, the governing equations of plates were simplified and a differential equation was obtained. Through the discussion of solutions to the differential equation, the critical buckling load can be got and will be reached before the reflection of the stress wave. The influence of plies angle on the critical buckling load was discussed. Comparing the new Ritz method with variable separation method, the critical buckling load curves of both methods are in good coincidence. The dynamic buckling of laminated composite plates with different plies angles were simulated and analysed by using ABAQUS. The maximum error is less than 5 percent and it indicates that the theoretical values are consistent with the simulated ones. The results show that the Ritz method combined with Abraham de Moivre’s formula is effective and feasible.

Key words:Abraham de Moivre’s formula; Ritz method; stress wave; the critical dynamic buckling load

基金项目：国家自然科学基金(11372209);山西省自然科学基金(2010011005)

收稿日期：2015-03-27修改稿收到日期：2015-05-13

通信作者韩志军 男，博士，教授，硕士生导师，1964年10月生

中图分类号:O344.1;TB33

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.10.029

第一作者 李楠 男，硕士生，1987年8月生