基于环境振动测试的框架结构主裙楼动力特性分析

刘　佩， 连鹏宇

(1. 北京交通大学 土木建筑工程学院, 北京　100044; 2.结构风工程与城市风环境北京市重点实验室, 北京　100044)

基于环境振动测试的框架结构主裙楼动力特性分析

刘佩1,2， 连鹏宇1

(1. 北京交通大学 土木建筑工程学院, 北京100044; 2.结构风工程与城市风环境北京市重点实验室, 北京100044)

摘要：对某未设防震缝的钢筋混凝土框架结构主楼和裙房进行环境振动测试，并对其动力特性进行分析。测点分别布置在主楼左右两个楼梯间、顶层楼板和裙房井字梁大跨楼板上。利用实测加速度数据并通过改进的频域分解法，识别得到了结构的五阶模态参数。识别结果表明：各测试方案得到的识别结果一致，自振频率的变异性较阻尼比的变异性小；前四阶模态由主楼的振动引起，第五阶模态为裙房楼板的一阶竖向振动模态；由于结构的不对称性，识别得到的前三阶振型均带有扭转效应；模态参数识别过程中的可疑模态可能来源于主楼和裙房的动力相互作用。建立了所测结构的有限元模型，得到了五阶自振频率和振型，与识别结果吻合较好；分析了主楼和裙房之间的不同连接方式对整体结构自振频率和振型的影响，结果表明主楼和裙房的固结连接与铰接连接对自振频率基本没有影响，而设置防震缝与否对自振频率影响较大，且振型出现顺序均不会发生变化。

关键词：环境振动测试；主裙楼；模态参数识别；频域分解法；动力相互作用

主裙楼是一种常用的建筑结构形式，在地震作用下主楼和裙房易发生相互碰撞。对于通过在主楼和裙房之间设置防震缝来避免地震作用下两者碰撞破坏的方法，一直以来都存有争议[1]。由于建筑使用功能上的需要，主楼和裙房之间一般不设防震缝，主裙楼连为一体，由于整体刚度不均匀，地震时将引起强烈的扭转效应[2-4]，因此在地震区采用这种建筑结构形式时其动力特性值得进一步探讨，以便为研究主楼和裙房之间的碰撞机制提供依据。

由于不需要昂贵的激振设备，不需要在实验室内搭建结构模型，不需要中断结构的正常使用，直接利用环境激励下的振动响应数据对结构进行监测近年来受到高度重视。利用环境振动测试数据，结合模态参数识别方法，可以对结构实际的动力特性进行评估，如相关学者开展的钢筋混凝土框架结构、框架剪力墙结构、塔、主次结构、耦合楼板体系，钢电视塔、古建塔、砌体结构等的环境振动测试和模态参数识别工作[5-13]。

本文通过对某未设防震缝的框架结构主裙楼足尺模型进行现场环境振动测试，利用改进的频域分解法对其模态参数进行识别，来对整体结构实际的动力特性进行评估；通过建立的经实测数据验证的有限元模型，对主裙楼之间的不同连接方式及设缝与否对整体结构动力特性的影响进行了分析，为该类结构进行动力有限元模型修正、预测地震作用下的响应提供依据，为研究其动力相互作用及碰撞机制提供参考。

1框架结构主裙楼环境振动测试

对某钢筋混凝土框架结构主裙楼进行了环境振动测试。所测主楼为办公楼，地上4层；裙房为大空间实验室，设有吊车梁并装有吊车，内部放置大型实验设备，层高约对应主楼两层层高，采用井字梁大跨楼盖，东西向长14.4 m，南北向长12.6 m；主楼和裙房之间无防震缝；主楼和裙房均无地下室，均采用柱下独立基础。所测主楼和裙房见图1(a)和(b)，平面示意图见图2，正立面图见图3，三层结构平面布置图见图4。

图1　所测钢筋混凝土框架结构主裙楼Fig.1 Tested main building and podium of reinforced concrete frame structure

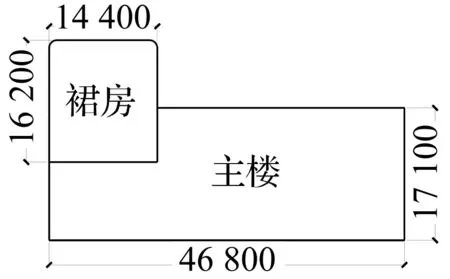
图2　所测主裙楼平面示意图(mm)Fig.2 Plan of the tested main building and podium(mm)

测试采用的振动信号采集设备为北京东方振动和噪声研究所出厂的INV3018C型8通道24位信号采集仪，利用软件DASP-V10对信号进行实时采集及记录。采用的传感器为中国地震局工程力学研究所出厂的941B型拾振器。

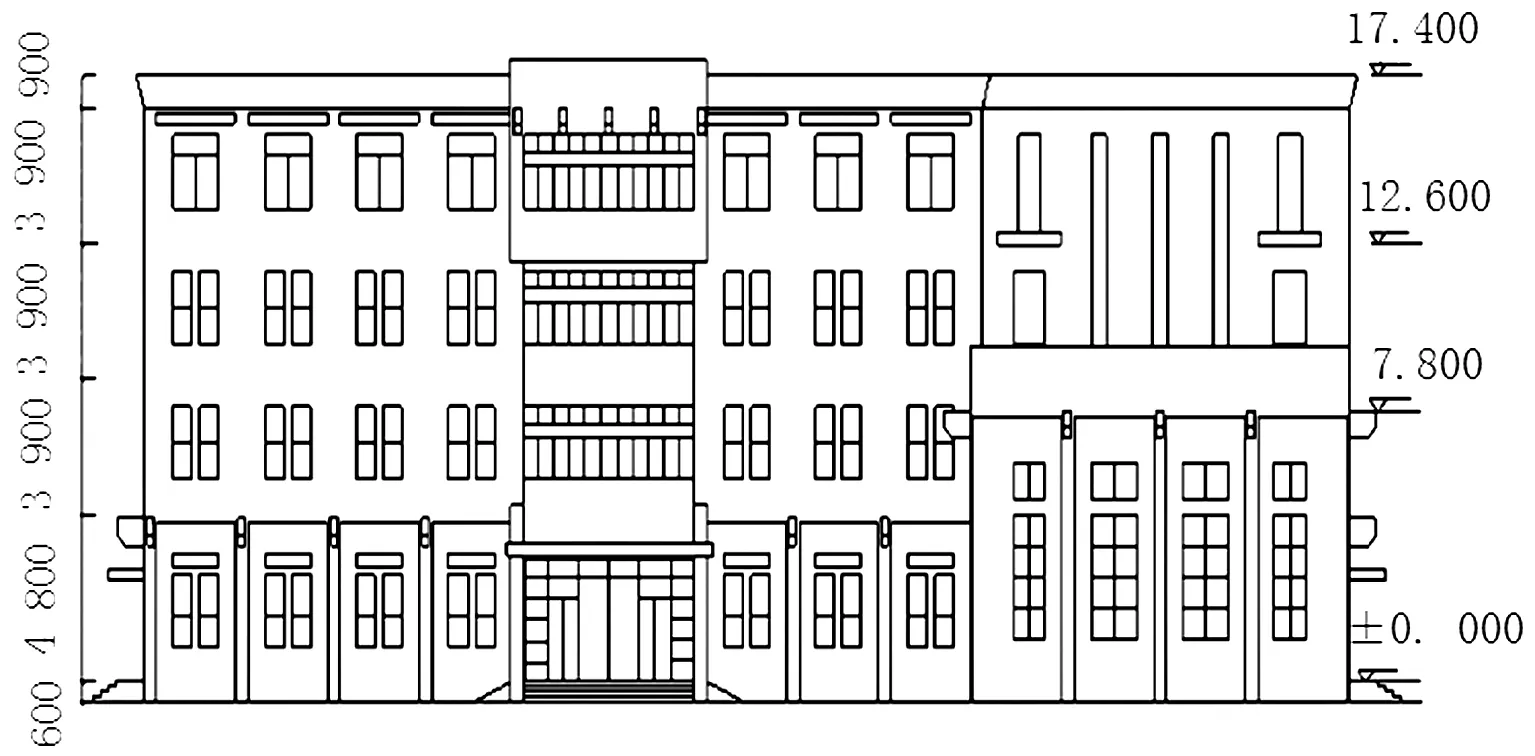
图3　所测主裙楼正立面图Fig.3 Elevation of the tested main building and podium

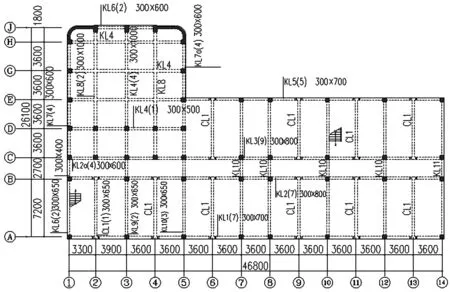
图4　三层结构平面布置图Fig.4 Structure layout of the third floor

图5　裙房楼板测点布置图Fig.5 Sensor array on the floor slab of the podium

测试分为以下五种工况进行：① 测点布置在主楼东侧(右侧)楼梯间，每层朝北(y向)和朝东(x向)各放置一个水平加速度传感器；② 测点布置在主楼西侧(左侧)楼梯间，每层朝北和朝东各放置一个水平加速度传感器；③ 测点布置在主楼四层楼道四个角点，各角点朝北和朝东各放置一个水平加速度传感器；④ 测点布置在裙房楼板顶部，在图5所示23个测点均布置竖向加速度传感器，由于测试通道数的限制，以7点为参考点，分三组进行测试：第一组测点包括7、8、9、12、14、17、18、19，第二组测点包括7、13、15、16、20、21、22、23，第三组测点包括7、1、2、3、4、5；⑤在图5所示7、9、17、19号测点朝北和朝东各放置一个水平加速度传感器。设置五种测试工况用于全面反应整体结构的动力特性，且各工况所得结果可相互验证。由于裙房为放置大型试验设备的实验室，且采用大跨井字梁楼盖，测试得到裙房楼板竖向自振频率，可以为防止由于设备振动引起楼板共振导致其开裂提供依据。

为了减小外界干扰对测试结果的影响，测试选在零点至凌晨5点进行。每种工况测试20 min，采样频率为512 Hz。裙房楼板测试之前部分测点布置如图6所示。根据环境振动测试所得各测点的加速度时程，利用改进的频域分解法可对所测主裙楼进行模态参数识别。

图6　裙房楼板上的部分测点Fig.6 Some sensors on the tested floor slab of podium

2模态参数识别的改进频域分解法

频域分解法[14]的基本思想为：利用奇异值谱的峰值识别得到结构的振型；利用奇异值谱峰值附近数据的相关函数的跨越零点次数确定自振频率；利用相关函数的包络线结合对数衰减技术得到阻尼比。由于数据的截断及理论依据不充分等原因，通过相关函数识别得到的自振频率和阻尼比误差较大，因此本文通过最小二乘技术[15]识别结构的自振频率和阻尼比，对频域分解法进行改进。

2.1振型的识别[14]

结构测试得到的响应y(t)与未知的输入x(t)之间的关系为

(1)

式中Gxx(iω)为输入功率谱密度矩阵；Gyy(iω)为响应功率谱密度矩阵；H(iω)为频响函数矩阵，上标“-”和“T”分别表示共轭和转置，通过极点-留数形式可表示为

(2)

式中M为振型数；λm=-σm+iωdm为第m阶极点，σm,ωdm分别为阻尼系数和阻尼模态频率；Rm为第m阶留数矩阵。

假定输入为白噪声，在特定频率处起控制作用的模态用Sub(ω)表示，对于阻尼比较小的结构，响应功率谱密度矩阵可以表示为

(3)

式中cm为实数标量，φm为第m阶振型。在第m阶模态处，上式可简化为

(4)

响应功率谱密度矩阵在ωk处的估计值通过奇异值分解可以表示为

(5)

式中S(ωk)为包含标量奇异值skj的对角阵， U(ωk)为包含奇异向量ukj的酉矩阵，j=1,…,M。

对结构响应功率谱密度矩阵进行奇异值分解得到奇异值谱曲线，在某个峰值处，若仅第m阶模态起控制作用，

(6)

则结构第m阶振型的估计值可通过最大奇异值对应的酉向量得到为

(7)

2.2自振频率及阻尼比的识别[15]

模态参数可以通过最大奇异值谱曲线得到，当峰值附近的两条谱线对应的奇异向量的相似度较高时，其奇异值属于同一模态，可以通过MAC进行判断。MAC定义为

(8)

其中‖ ‖为2范数；ur1为峰值谱线处的奇异向量，uk1为峰值谱线频率附近点ωk对应的奇异向量。当MACk≥Ω时(可设Ω=0.85～0.95)，认为ωk点与峰值谱线点为同模态的点。

对比式(4)和式(6)，得

即

将其整理成矩阵形式为

(9)

设该第m阶模态峰值谱线附近满足MAC值条件的频率点为ωk(k=1,2,…,p)，对应的最大奇异值为sk1，分别代入式(9)形成如下矩阵方程：

Ax=y

(10)

其中：

(11)

其最小二乘解为：

x=(ATA)-1ATy

(12)

3模态参数识别结果

根据环境振动测试所得加速度时程，计算得到各工况的功率谱密度(PSD)及最大奇异值(SV)谱曲线见图7。其中计算功率谱密度时采用平均周期图法，快速傅里叶变换数据点数取8 192，加汉明窗，窗长取8 192，重叠部分的数据点数取8 192/4。

利用改进的频域分解法，识别得到的各阶频率和阻尼比见表1和表2，可以看出各种工况识别得到的结果一致，第2阶模态在工况5中及第3阶模态在工况2中未识别得到，可能与这两种工况测点布置位置对相应振型不敏感且测试时环境振动信号的相应模态信噪比不高有关；各阶自振频率的变异性明显小于阻尼比的变异性，说明自振频率的识别精度较高，而由于结构的阻尼机制较为复杂，故阻尼比的识别精度相对较差，但识别得到的阻尼比均小于0.05，符合混凝土材料的阻尼特性。

图7　各测试工况的功率谱密度和最大奇异值谱Fig.7 Power spectral density and the maximum singular value spectra for all the cases

Hz

表2　各工况识别得到的阻尼比

由工况1和工况4识别得到的各阶振型见图8，可以看出所测结构的第1阶振型由主体结构的y向一阶平动引起，伴随一定的扭转效应；第2阶振型由主体结构的x向一阶平动引起，伴随一定的扭转效应；第3阶振型由主体结构的扭转引起；第4阶振型由主体结构的y向二阶平动引起；第5阶振型由裙房楼板的局部振动引起，为其一阶竖向弯曲振型，可以看出该振型很好的被识别得到，这与传感器的精确布置有很大关系，该振型为利用工况4的三组数据通过参考点组合得到。

在模态参数识别过程中，由于机械设备振动、外界扰动、电磁干扰等因素会引起噪声模态，如果这些噪声模态远离结构的真实模态，则不会对识别结果造成影响，如工况1、工况2、工况3、工况5的奇异值谱曲线在频率7 Hz附近出现的峰值，以及工况4第一组、工况4第三组、工况5的奇异值谱曲线在频率14 Hz附近出现的峰值，这些峰值对应的模态是由于谐振频率产生的噪声模态，这类峰值非常陡峭，并且对应的阻尼比非常小。另外，对于土木工程结构来说，由于相邻结构的动力相互作用也可能产生噪声模态[16]，如工况3的奇异值谱曲线在2.5～5 Hz、工况5的奇异值谱曲线在2.5～5 Hz和10.5～12.5 Hz之间出现了许多比较接近的峰值，这些峰值对应的模态有一些是结构的固有模态，另外一些可能是由于主楼和裙房的动力相互作用产生的。

图8　识别得到的各阶振型Fig.8 Identified mode shapes

4有限元模型模态分析结果

利用sap2000建立有限元模型，计算模型的钢筋混凝土梁、柱、楼板均采用C30混凝土，梁柱的纵筋采用HRB335级钢筋，箍筋采用HPB235级钢筋，板内配筋均采用HPB235级钢筋；主楼楼板厚120 mm，裙房楼板厚80 mm；填充墙采用炉渣盲孔空心砖，外墙厚300 mm，内墙厚200 mm；主楼框架柱截面尺寸为500 mm×500 mm，裙房框架柱截面尺寸为800 mm×500 mm，梁截面尺寸见图4。

计算模型的基本假定为：① 仅考虑上部结构，计算模型底部固接；② 梁、柱、楼板均为线弹性体；③ 考虑填充墙对结构抗侧刚度的影响；④ 结构楼板上施加均布荷载且按测试时的实际情况考虑。

计算模型具体的计算参数见表3。

表3　有限元模型计算参数

梁和柱通过框架单元进行模拟；楼梯简化为斜板进行模拟，且楼梯斜板、楼板、剪力墙和填充墙通过壳单元进行模拟。

利用所建有限元模型得到整体结构的五阶自振频率见表4，可以看出计算所得前三阶自振频率与识别结果吻合较好，第4阶自振频率与识别结果存在一定的误差，第5阶自振频率与识别结果之间的误差居中。

计算所得整体结构的五阶振型见图9，可以看出前四阶振型均为由主体结构振动引起的整体振动，第5阶振型为裙房楼板的局部振动，与识别结果一致，前两阶振型的扭转效应与识别结果相比不明显。

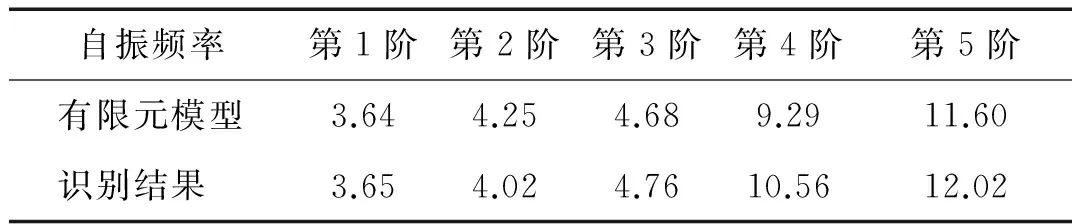
表4　有限元模型计算所得自振频率

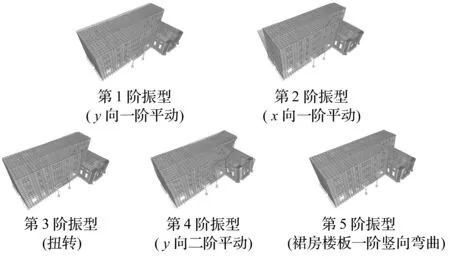
图9　有限元模型计算所得振型Fig.9 Mode shapes calculated from the finite element model of the tested structure

以所建的主楼与裙房固接模型为基准，计算了主楼和裙房之间采用不同连接方式时整体结构的自振频率，具体结果见表5，其中主楼与裙房铰接模型与固接模型相比释放了交界处x向梁的扭矩以及主楼楼板y向梁的弯矩，设置防震缝模型为设缝后的主楼模型，此时主楼和裙房假定为两个独立部分。从表5中可以看出主楼和裙房之间采用固接连接还是铰接连接对整体结构的自振频率基本没有影响；设置防震缝后主楼的前三阶自振频率较主裙楼小，而第4阶频率则基本没有变化，说明裙房对提高整体结构的刚度贡献较大，影响整体结构的一阶模态，而对二阶模态基本没有影响；设置防震缝后裙房楼板一阶竖向自振频率为11.27 Hz，较主裙楼小，说明主楼对裙房楼板的抗弯刚度有较大影响。三种不同的连接方式对振型的出现顺序没有影响。

表5　主楼和裙房之间采用不同连接方式时结构的自振频率

5结论

本文对某钢筋混凝土框架结构主裙楼进行了五种工况的环境振动测试，并对其模态参数进行了识别，结果表明：各测试方案得到的识别结果一致，自振频率的变异性较阻尼比的变异性小；前四阶模态由主楼的振动引起，第5阶模态为裙房楼板的一阶竖向振动模态；由于结构的不对称性，识别得到的前三阶振型均带有扭转效应；模态参数识别过程中的可疑模态可能来源于主楼和裙房的动力相互作用。

建立了所测无防震缝框架结构主裙楼的有限元模型，得到了五阶自振频率和振型，与识别结果吻合较好；分析了主楼和裙房之间的不同连接方式对整体结构自振频率和振型的影响，结果表明主楼和裙房的固结连接与铰接连接对自振频率基本没有影响，而设置防震缝与否对自振频率影响较大，且振型出现顺序均不会发生变化。

所测裙房井字梁大跨楼板竖向弯曲模态的识别有助于避免机械设备的振动引起楼板的共振，造成楼板的开裂。利用模态参数识别结果对所建有限元模型进行后续的修正可进一步提高有限元模型的精度，使其更符合实际情况。研究结果为该类主裙楼结构的动力相互作用特性、在地震作用下的反应预测及碰撞机制研究提供了基础。

参 考 文 献

[1] 张保良, 张鹏飞. 带裙房高层建筑的沉降缝设置探讨[J]. 建筑结构, 1996, 26(6): 21-26.

ZHANG Bao-liang, ZHANG Peng-fei.Discussion on presence of settlement joint for high-rise buildings with podium [J]. Building Structure, 1996, 26(6): 21-26.

[2] 刘德稳, 郭春丽, 陈虎, 等. 主裙楼不同连接方式对L型带裙房高层建筑结构-基础-地基共同作用影响研究[J]. 科学技术与工程, 2013, 13(21): 6156-6163.

LIU De-wen, GUO Chun-li, CHEN Hu, et al. Concurrent functional influence research of L-shaped podiums high-rise structure connected in different ways [J]. Science Technology and Engineering, 2013, 13(21): 6156-6163.

[3] 郗俊玲. 高层建筑结构主体与裙楼非独立布置方案研究[D]. 西安：西安理工大学, 2008.

[4] 刘晶波, 汪勇. 主-裙楼结构体系的动力特性及地震反应分析[J]. 建筑结构学报, 2000, 21(2): 36-43.

LIU Jing-bo, WANG Yong. Dynamic properties and seismic response of high-rise building with podium [J]. Journal of Building Structures, 2000, 21(2): 36-43.

[5] Soyoz S, Taciroglu E, Orakcal K, et al. Ambient and forced vibration testing of a reinforced concrete building before and after its seismic retrofitting [J]. ASCE Journal of Structural Engineering, 2013, 139(10): 1741-1752.

[6] Sahin A, Bayraktar A, Özcan D M, et al. Dynamic field test, system identification, and modal validation of an RC Minaret: preprocessing and postprocessing the wind-induced ambient vibration data [J]. ASCE Journal of Performance of Constructed Facilities, 2011, 25(4): 336-356.

[7] Au S K, Zhang F L. Ambient modal identification of a primary-secondary structure by fast Bayesian FFT method [J]. Mechanical Systems and Signal Processing, 2012,28(4): 1318-1325.

[8] Au S K, Ni Y C, Zhang F L, et al. Full scale dynamic testing and modal identification of a coupled floor slab system [J]. Engineering Structures, 2012, 37(4): 167-178.

[9] Chen W H, Lu Z R, Lin W, et al. Theoretical and experimental modal analysis of the Guangzhou New TV Tower [J]. Engineering Structures, 2011, 33(12): 3628-3646.

[10] Foti D, Diaferio M, Giannoccaro N I, et al. Ambient vibration testing, dynamic identification and model updating of a historic tower [J]. NDT & E International, 2012,47(4): 88-95.

[11] 孙雷, 刘福胜, 王少杰, 等. 短周期村镇砌体建筑振动特性实测与抗震性能分析[J]. 土木工程学报, 2013,46(增刊2): 57-62.

SUN Lei, LIU Fu-sheng,WANG Shao-jie, et al. Dynamic characteristic test and seismic performance analysis of short-period masonry [J]. China Civil Engineering Journal, 2013, 46(Sup2): 57-62.

[12] 非明伦, 周光全, 卢永坤,等. 昆明高(超高)层建筑环境振动特性实测与统计分析[J]. 地震研究, 2012, 35(1): 117-127.

FEI Ming-lun, ZHOU Guang-quan, LU Yong-kun, et al. Actual measurement and statistical analysis of ambient vibration characteristics of the high-rise (skyscraper) buildings in Kunming [J]. Journal of Seismological Research, 2012, 35(1): 117-127.

[13] 施卫星, 王进. 钢筋混凝土框架结构动力特性研究[J]. 地震工程与工程振动, 2010, 30(6): 87-91.

SHI Wei-xing, WANG Jin. Research on dynamic characteristics of reinforced concrete frame structures [J]. Journal of Earthquake Engineering and Engineering Vibration, 2010, 30(6): 87-91.

[14] Brincker R, Zhang L M, Anderson P. Modal identification of output-only systems using frequency domain decomposition [J]. Smart Materials and Structures, 2001,10(3):441-455.

[15] 陈刚，吴小辰，柳勇军,等. 基于频域分解法和广域稳态量测的低频振荡模式辨识[J]. 电力系统保护与控制, 2011, 39(12): 1-6.

CHEN Gang, WU Xiao-chen, LIU Yong-jun, et al. Identification of low-frequency oscillation modes based on frequency domain decomposition method and wide area ambient measurement [J]. Power System Protection and Control, 2011, 39(12): 1-6.

[16] Michel C, Guéguen P, Bard P Y. Dynamic parameters of structures extracted from ambient vibration measurements: an aid for the seismic vulnerability assessment of existing buildings in moderate seismic hazard regions [J]. Soil Dynamics and Earthquake Engineering,2008,28(8):593-604.

Dynamic characteristics analysis of a frame structure with the main building and podium based on ambient vibration test data

LIU Pei1,2, LIAN Peng-yu1

(1. School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China;2. Beijing’s Key Laboratory of Structural Wind Engineering and Urban Wind Environment, Beijing 100044, China)

Abstract:Ambient vibration tests of a frame structure consisting of the main building and podium without seismic joint were conducted and the dynamic characteristics of the structure were analyzed. The sensors employed in the tests were mounted on the right and left stairwells, the fourth floor of the main building and the large span floor of the podium with grillage beams. With the measured acceleration data and by using an improved frequency domain decomposition method, the modal parameters of five modes were identified. Consistent identification results were obtained by different test schemes. The fluctuation of identified natural frequencies is smaller than that of damping ratios. The first four modes are induced by the vibration of the main building. The fifth mode is the first vertical bending mode of the podium. The torsional behavior appears in the first three modes due to the asymmetry of the structure. The spurious modes during identification may be due to the dynamic interactions between the main building and podium. A finite element model of the tested structure was constructed and five modes were obtained, which agree well with the identification results. The influence of different connection forms between the main building and podium on the natural frequencies and mode shapes of the structure were analyzed. Results show that fixed or pinned connections between the main building and podium have almost no influence, while presence of seismic joint has large influence on the natural frequencies of the structure. The order of the mode shapes does not change for all the cases.

Key words:ambient vibration test; main building and podium; modal parameter identification; frequency domain decomposition method; dynamic interaction

基金项目：中央高校基本科研业务费 (2014JBM100) 资助项目

收稿日期：2015-04-15修改稿收到日期：2015-05-26

中图分类号:TU311

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.10.028

第一作者 刘佩 女，博士，副教授，1982年12月生

E-mail: liupei0130@126.com