基于双树复小波的重叠块阈值降噪方法

吴定海, 张培林, 杨望灿, 齐蕴光

(军械工程学院 车辆与电气工程系,石家庄　050003)

基于双树复小波的重叠块阈值降噪方法

吴定海, 张培林, 杨望灿, 齐蕴光

(军械工程学院 车辆与电气工程系,石家庄050003)

摘要：针对机械早期故障信号受到强背景噪声影响导致故障特征不明显的问题，提出一种基于双树复小波包的重叠块阈值降噪方法。利用有限冗余双树复小波包变换对信号进行具有平移不变性的稀疏分解，结合双树复小波包变换系数所具有的稀疏集簇和邻域相关性特点，建立重叠块阈值估计模型，通过最小化包含块稀疏模型的适应度函数获得估计信号，分析了重叠块阈值降噪各参数对降噪效果的影响和参数优化原则，仿真与实测信号实验结果表明，该方法在不同信号和不同噪声水平下均有效地抑制了噪声干扰，提高了信噪比。

关键词：机械振动；状态监测；重叠块阈值；双树复小波包；降噪

复杂装备机械系统经常在复杂恶劣工况下运行，其核心部件如发动机、变速箱不可避免地产生不同程度的损伤或故障。为避免重大事故，开展机械在线监测与故障诊断研究具有重要意义。振动监测是行之有效的手段，然而机械故障信号往往被强背景噪声所淹没，造成征兆不明显，信号特征较微弱，大大增加了设备在线故障的识别难度[1-2]。

小波变换被广泛运用于机械信号处理，振动信号在小波域进行稀疏分解，基于信号与噪声在不同分解尺度上不同传递特性进而实现信噪分离。在小波变换系数处理方法方面，阈值处理方法如统一阈值、无偏估计阈值等，具有处理速度快、效率高被广泛应用到在线监测信号处理中。以往的信号处理都是考虑单个系数和逐一进行处理，Chen等[3]考虑了邻域小波系数的影响，提出了重叠块阈值的信号降噪方法，以一个系数块为单位进行考虑和处理，进一步提高阈值估计的精度和去噪效果。

受到传统离散小波变换下抽样而导致伪吉布斯现象的影响和限制，近年来，许多学者主要研究利用冗余小波变换[4-5]如非下抽样小波变换、多小波变换等所具有的平移不变性来提高信号处理的效果，但同时数据运算量也大为增加。

信号的稀疏分解不仅有利于数据压缩，更有利于后续的降噪和特征提取。本文结合双树复小波的平移不变性、小波系数稀疏集簇和邻域相关特性，提出了基于双树复小波包的重叠块阈值降噪方法，通过最小化凸优化函数获得估计信号，避免人工分块对降噪效果的影响，并分析了该降噪算法的参数优化原则，仿真和实测信号验证了该方法的有效性。

1双树复小波包的信号稀疏分解

双树复小波变换是一种有限冗余的信号处理方法，具有近似平移不变性[6-7]，降低了冗余度和计算量。双树复小波包二层分解与重构过程如图1所示。

图1　双树复小波包二层分解与重构过程Fig.1 Decomposition and reconstruction of two level DT-CWPT

为实现这样的特性，双树复小波包变换采用两棵并行的实小波变换树来实现对信号的分解，分别为树a和树b，树b的采样部位始终位于树a的中间，实现两棵树的信息互补。

双树复小波变换的系数以树a为实部，以树b为虚部，可表示为：

(1)

式中，l为变换尺度因子，J为最大变换尺度。

第一层分解采用非下抽样小波变换，滤波器采用传统的滤波器组，进行奇偶分离后，分别进行基于Mallat算法的分解与重构，第二层以上双树复小波包节点尺度或小波系数表示如下：

(2)

(3)

信号重构时对树a和树b进行联合重构：

(4)

第二层以上分解与重构的关键是滤波器组形成Hilbert变换对：

ψg(t)=H[ψh(t)]

(5)

即在对应滤波器构造时形成半采样延迟：

g0(n)≈h0(n-0.5)

(6)

2重叠块阈值降噪方法

对于原始信号x，叠加的噪声假设为高斯白噪声w，则含噪信号y可表示为：

y(i)=x(i)+w(i)i∈I

(7)

小波分解变换后的小波系数，具有一定的统计规律，可以用非高斯多参数概率密度模型来表示：

x∈Rd

(8)

对于通过收缩阈值函数的方法来估计x通常可以表示成以下优化问题[3]：

(9)

对于双树复小波变换后的系数，不仅具有稀疏特性，而且具有集簇特性，变换域的相邻系数之间存在一定的联系，若其相邻的小波系数的幅值较大时，那么该点的小波系数幅值也较大，针对以上特点，重叠块阈值的降噪方法，对小波系数进行阈值处理不是逐个处理，而是先进行分块，再逐块处理，阈值估计时，考虑到邻域小波系数的影响，可通过一个滑动窗(长度为k)对系数进行分块处理，J代表分块。惩罚函数可以表示成：

(10)

式中，i是小波系数块的索引，i={0,1,…,N-1}，j是系数块i中的小波系数索引，j={0,1,…,K-1}。对于块边缘采用补零的方式处理。

F(x)=

(11)

因此，可以获得该信号的适应度函数F(x)，且容易证明该函数为凸函数。对式(11)求偏导，得

(12)

令偏导为0，进而可以求解得到

(13)

基于双树复小波包变换的重叠块阈值降噪方法，主要涉及到3个参数，即分块长度、迭代次数、λ，参数的选择直接影响到信号降噪的效果。

从式(12)来分析，可知λ与信号降噪后的信噪比相关，但是两者并没有直接确定的关系表达式，那λ该如何选取，才能保证所有的噪声被消除？无法像软阈值那样来确定阈值的大小T，但是λ的取值却与原信号的噪声水平息息相关，令

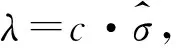
(14)

则λ的取值转化为信号噪声方差系数c，在重叠块阈值中，λ和重叠块k均影响到了阈值的大小，应该综合来考虑。以Heavysine仿真信号为例，图2给出了参数λ和重叠块k对降噪后信噪比的影响，(迭代次数选择为10)，可知c和k的取值相对于信噪比的变化趋势都是先增大后减小，在联合分布中取信噪比最大时的c和k，确定为[0.37,6]。

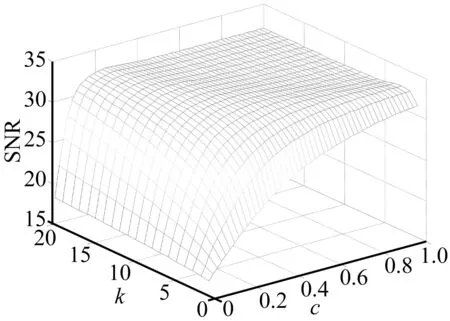
图2　参数λ与重叠块k对信噪比的影响Fig.2 Effect of parameter λ and overlappling group k for signal noise ratio

重叠块阈值采用迭代优化，根据降噪原理，随着迭代次数N的增加，系数x可由以下公式获得

(15)

根据上述公式，进而可以推导出，初始值为0的系数在迭代过程中始终为0，非零系数在迭代过程中始终非零，那么该方法如何实现降噪呢？对于被认为是噪声的小系数，由于考虑了邻域系数的影响，在迭代过程中迅速减小，逐渐趋近于0，从而实现抑制噪声干扰的作用。

(16)

通过大量仿真分析发现，在迭代一定程度以后，迭代次数N的变化对λ和k的选择影响并不大，可以最后进行优选，因此，参数优化原则为：先确定好λ和重叠块k，再优化迭代次数N，以适应度函数最小值为标准选择合适的迭代次数。

3计算结果分析与比较

3.1仿真信号分析

下面用典型的非平稳信号heavysine信号、doppler信号、blocks信号、bumps信号来验证本文降噪方法的效果，通过加入白噪声生成具有不同信噪比的含噪信号，并采用双树复小波包变换方法进行分解，用重叠块阈值方法进行降噪处理，并通过2.2节确定和优化相关参数，降噪效果如图3～图6所示，并引入信噪比(SNR)和均方误差(RMSE)作为评价标准。

图3　Heavysine信号的双树复小波包降噪Fig.3 Denoising of Heavysine signal based on DT-CWPT

图3～图6列出了4种仿真信号的降噪效果。由图3所知，对于信噪比为17.165 8 dB的Heavysine信号，经过本文方法降噪后，噪声信号明显得到良好的抑制，信噪比提升至32.799 4 dB，相比之下，文献[7]能够将Heavysine染噪信号的信噪比由17dB优化至27.146 9 dB。

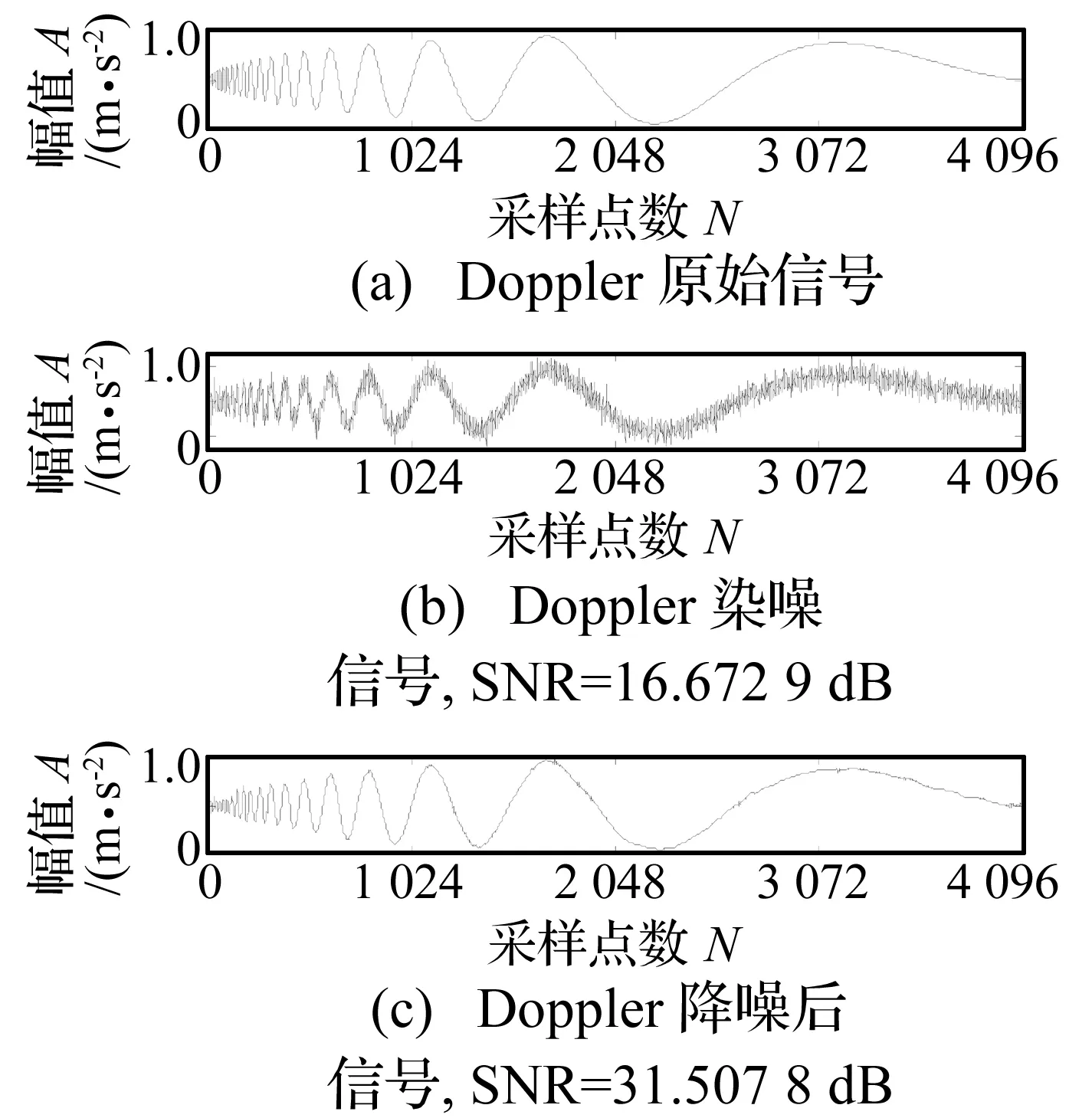
图4　Doppler信号的双树复小波包降噪Fig.4 Denoising of Doppler signal based on DT-CWPT

在图4中，对于信噪比为16.672 9 dB的Doppler信号，降噪后信噪比提升至31.507 8 dB，对比文献[8]方法能够将Doppler染噪信号的信噪比由16 dB提升至26.441 9 dB，本文降噪方法具有较好的效果。

对于Blocks信号，文献[9]方法能够将Blocks染噪信号的信噪比由15 dB提升至21.27 dB，而本文可以优化至25.559 1 dB，可知本文方法能够较好地去除背景噪声，抑制波形失真，保留有用信息。

另外，为测试本降噪方法在低信噪比条件下的降噪能力，图6设置仿真信号Bumps染噪信噪比为0.83 dB，经本文方法降噪后，信噪比可提升至11.930 5 dB，说明在较低信噪比条件下，本文降噪方法同样能够取得较好的降噪效果。

表1列出了利用本文降噪方法对不同信噪比典型非平稳信号的降噪效果， 给出了优化后的各参数和降

图5　Blocks信号的双树复小波包降噪Fig.5 Denoising of Blocks signal based on DT-CWPT

图6　Bumps信号的双树复小波包降噪Fig.6 Denoising of Bumps signal based on DT-CWPT

噪结果，通过对比，本文所提降噪方法要明显优于文献[8-9]的方法，有效地抑制了噪声的干扰，更好地保留了波形特征，取得更优的降噪效果。

表1　典型非平稳信号的降噪效果

3.2实测信号分析

实测振动信号来自一个滚动轴承故障模拟实验台，加速度传感器安装在轴承座上，电动机转速控制在1 772 r/min左右，轴承型号为SKF6205，滚动轴承在轴承内圈、外圈和滚动体上分别加工一个微小的沟槽来模拟早期故障，采样频率为12 kHz，轴承内圈故障频率为160.0 Hz。

轴承内圈故障的原始时域波形和频谱如图7所示，由于故障较为微弱，轴承运动时产生的冲击被淹没在强背景噪声下。从原信号的频谱(只给出0～500 Hz频段)中没能体现出相应的故障特征频率，难以直接判别该滚动轴承是否存在故障。

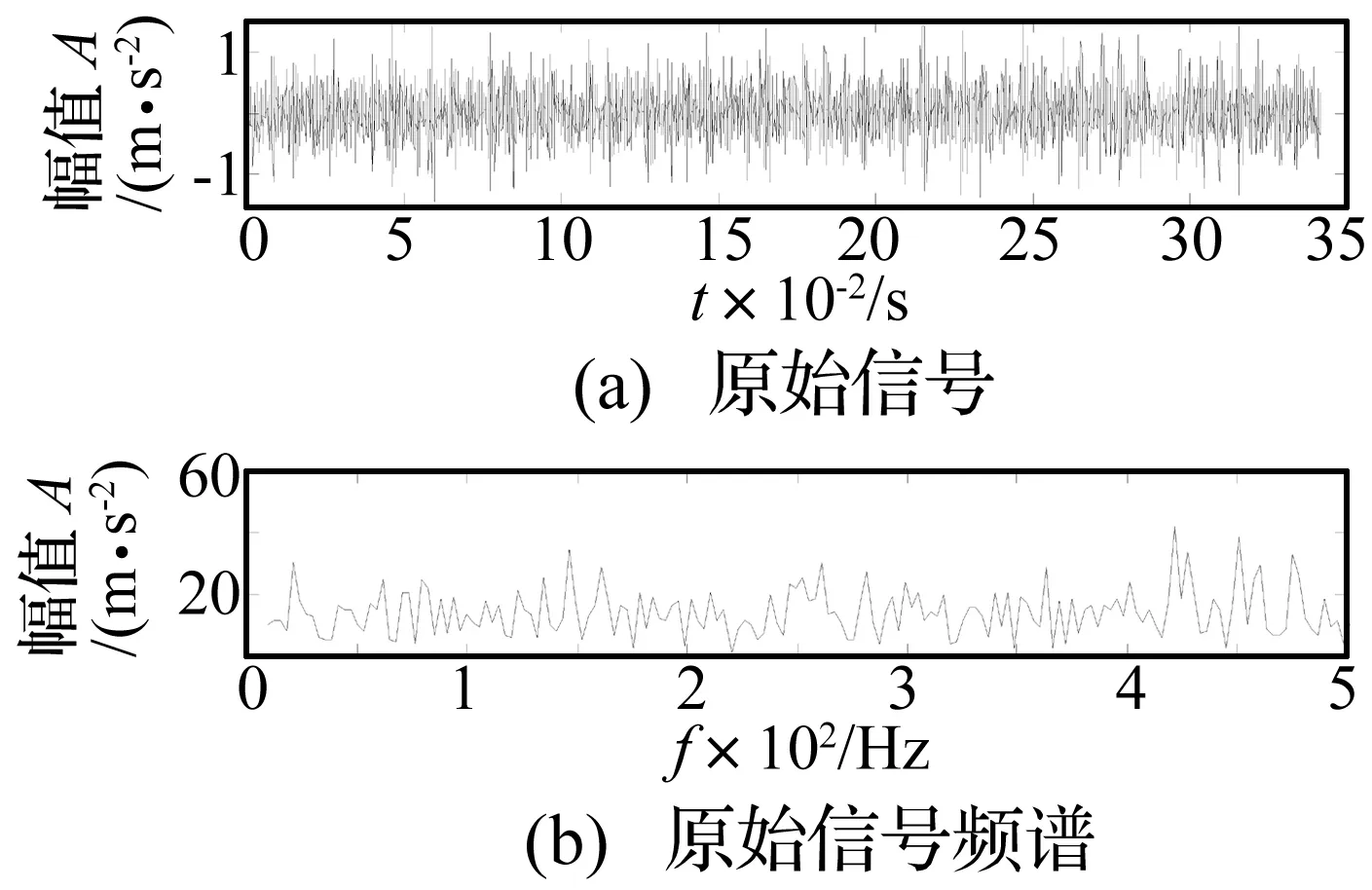
图7　实测故障信号及频谱Fig.7 Signal and frequency spectrum of bearing fault

为突出故障特征，图8首先采用双树复小波包的Neighcoeff分块阈值降噪方法对信号进行降噪，分解层数设置5层，获得降噪后信号和包络频谱，由图可见噪声被大量去除，但从频谱来看仅保留了转频的2倍频60 Hz，故障信息被当作噪声滤除，未能识别其他有效信息。

图8　双树复小波包分块阈值降噪后信号及频谱Fig.8 Denoised signal and frequency based on daul-tree complex wavelet packet transform and NeighCoeff

采用本文方法对该故障信号进行分析，分解层数设置5层，重叠块长度选择为3，噪声方差系数c取0.45，迭代次数为15，降噪后的信号及包络谱如图9所示。从时域图中可以看到，降噪后，信号机械冲击特征得到较好的保留，周期性特征较为明显，信号中的故障信息已经突显出来，对其进行包络解调，从包络谱图中可以清晰地看到倍频60 Hz和故障频率160 Hz，与轴承内圈故障频率一致，而且干扰频率很少。

图9　本文方法降噪后信号及频谱Fig.9 Denoising signal and frequency based on the proposed method

4结论

(1) 提出基于双树复小波包变换的重叠块阈值降噪方法，重叠块阈值降噪方法利用分块和迭代计算，有效地利用了双树复小波包变换系数间的相关性特征，结合了双树复小波包变换所具有的平移不变性，提高了信号的降噪效果。

(2) 重叠块阈值降噪方法包括参数较多，体现阈值水平的λ和分块长度k对信噪的降噪效果具有较大的影响，需合理选择。

(3) 本文降噪方法能够有效抑制早期机械故障信号中强背景噪声，突出有用信息，对提高早期故障特征提取能力具有重要意义。

参 考 文 献

[1] 陈彬强, 张周锁, 何正嘉. 双密度双树复小波变换及其在机械故障微弱特征提取中的应用[J]. 机械工程学报, 2012, 48 (9): 57-63.

CHEN Bin-qiang, ZHANG Zhou-suo, HE Zheng-jia.Enhancement of weak feature extraction in mechinery fault diagnosis by using double density dual tree complex wavelet transform[J]. Journal of Mechanical Engineering,2012,48(9):57-63.

[2] 孙海亮, 訾艳阳, 袁静,等. 非抽样多小波和Hilbert-Huang时频分析在行星减速器早期故障诊断中的应用[J]. 机械工程学报, 2013, 49 (2): 56-63.

SUN Hai-liang, ZI Yan-yang, YUAN Jing, et al.Undecimated multiwavelet and Hilbert-Huang time-frequency analysis and its application in the incipient fault diagnosis of planetary gearboxes[J]. Journal of Mechanical Engineering, 2013,49(2): 56-63.

[3] Chen P Y, Selesnick I W. Translation-invariant shrinkage/thresholding of goup sparse signals[J]. Signal Processing, 2014, 94: 476-489.

[4] Chen Jing-long, Zi Yan-yang, He Zheng-jia, et al. Adaptive redundant multiwavelet denoising with improved neighboring coefficients for gearbox fault detection[J]. Mechanical Systems and Signal Processing, 2013,38: 549-568.

[5] Wang Xiao-dong, Zi Yan-yang, He Zheng-jia. Multiwavelet denoising with improved neighboring coefficients for application on rolling bearing fault diagnosis[J]. Mechanical Systems and Signal Processing, 2011,25:285-304.

[6] Barri A, Dooms A, Schelkens P. The near shift-invariance of the dual-tree complex wavelet transform revisited[J]. Journal of Mathematical Analysis and Applications,2012,389:1303-1314.

[7] 吴定海, 张培林, 任国全,等. 基于双树复小波包的发动机振动信号特征提取研究[J]. 振动与冲击, 2010, 29(4): 160-165.

WU Ding-hai, ZHANG Pei-lin, REN Guo-quan, et al. Feature extraction of an engine vibration signal based on dual-tree wavelet package transformation[J]. Journal of Vibration and Shock, 2010, 29 (4): 160-165.

[8] 陈志新, 徐金梧, 杨德斌. 基于复小波块阈值的降噪方法及其在机械故障诊断中的应用[J]. 机械工程学报, 2007, 43(6): 200-205.

CHEN Zhi-xin, XU Jin-wu, YANG De-bin.Denoising method of block thresholding based on DT-CWT and its application in mechanical fault diagnosis[J]. Journal of Mechanical Engineering, 2007, 43(6): 200-205.

[9] 向东阳, 吴正国, 侯新国,等. 改进的多小波变换系数相关去噪算法[J]. 高电压技术, 2011, 37(7): 1728-1733.

XIANG Dong-yang, WU Zheng-guo, HOU Xin-guo, et al. Improved denoising method using the correlation of multiwaveleti coefficient[J]. High Voltage Engineering,2011, 37(7): 1728-1733.

Overlappling group thresholding denoising method based on dual-tree complex wavelet packet transform

WU Ding-hai, ZHANG Pei-lin, YANG Wang-can, QI Yun-guang

(Department of Vehicle and Electrical Engineering, Ordnance Engineering College, Shijiazhuang 050003, China)

Abstract:In order to solve the problem that the early mechanical fault characteristics are usually indistinct due to strong background noise, an overlappling group thresholding denoising method based on dual-tree complex wavelet packet transform was proposed. The signal was sparsely decomposed by using the dual-tree complex wavelet packet which has the characteristic of shift-invariant and limited redundancy. The overlappling group thresholding denoising method based on dual-tree complex wavelet packet transform was developed which can capture the neighborhood correlation and large-amplitude coefficients form clusters, and a denoising model was built based on the minimization of a convex cost function incorporating with a mixed norm. Then the parameters optimization of the denoising model was discussed. The simulation and experimental results show that the noise reduction effect of the presented method is satisfactory for different signals with different level of noise, the background noise is restrained effectively and the signal noise ratio can be well improved.

Key words:machinery vibration; condition monitoring; block threshloding; dual-tree complex wavelet transform; denoising

基金项目：国家自然科学基金资助项目(51305454)

收稿日期：2015-04-08修改稿收到日期：2015-05-26

中图分类号:TH165；TP206

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.10.026

第一作者 吴定海 男，博士，讲师，1981年10月生

E-mail：wudh81@163.com