滚动轴承复合故障诊断的自适应方法研究

马新娜, 杨绍普

(1.石家庄铁道大学 信息科学与技术学院，石家庄　050043； 2.石家庄铁道大学 机械工程学院，石家庄　050043)

滚动轴承复合故障诊断的自适应方法研究

马新娜1, 杨绍普2

(1.石家庄铁道大学 信息科学与技术学院，石家庄050043； 2.石家庄铁道大学 机械工程学院，石家庄050043)

摘要：铁路货车滚动轴承检测中多种故障共存的情况普遍存在。针对单通道情况下复合故障难分离和诊断的问题，提出了基于陷波器的自适应复合故障诊断方法。该方法首先对滚动轴承的复合故障振动信号进行经验模态分解(Empirical Mode Decomposition, EMD)，根据各个本征模态函数与原始信号的相关系数最大化原则对信号进行重构，进一步通过频谱分析识别出滚动轴承主故障。在此基础上，利用自适应陷波器系统对原始振动信号的主故障信号进行陷波处理。然后再对筛去主故障信息的信号进行次故障诊断。通过仿真和实验分析，结果表明基于陷波器的自适应复合故障诊断方法能在一定程度上满足复合故障信号分离和故障诊断的要求，具有一定的实用性。

关键词：复合故障;滚动轴承;陷波器;经验模态分解

滚动轴承是旋转机械设备中的常见零部件，其运行状态直接影响着整个系统的性能。因此，对滚动轴承的状态监测和故障诊断是十分有必要的[1]。针对滚动轴承单一故障的特征提取，研究人员提出了共振解调[2]、小波变换[3-4]、快速谱峭度[5]以及经验模态[6]等方法，并取得了较好的应用效果。但在铁路车辆检修过程中，同一个滚动轴承多种故障并存的现象普遍存在。对多种故障形成的复合信号进行分离是正确判断复合故障的前提[7-9]。Anton等[10-11]提出的盲源信号分离方法有较好的效果，但状态监测的实际环境往往不能满足多通道检测的需求。沈国际等[12-13]研究发现，复合故障形成的多源振动信号并不一定具备利用经验模态方法正确分解的充分条件。胥永刚等[14-16]研究了小波在复合故障诊断中的应用，但是小波基的选择和分解层次的确定具有很大难度。

在分析复合信号频率特征基础上，结合滚动轴承复合故障特征，利用陷波器对信号的过滤作用，提出了基于陷波器的滚动轴承复合故障诊断的自适应方法，用于研究轴承复合故障的分离与诊断问题。通过大量的仿真和实例分析，表明基于陷变器的自适应诊断方法能较好地分离复合故障，具有一定的应用价值。

1自适应陷波器

陷波器是一种特殊的滤波器，理想情况下其阻带只有一个频率点。理想陷波器的频率特征只在陷波频率处等于1，其他频率处为0[17]。理想陷波器的设计必须满足两个基本条件[18]：

(1) 为使陷波器在陷波频率处的衰减无穷大，传递函数z的零点在单位圆上。即传递函数的分子多项式系数具有对称性：

A(z-1)=1+a1z-1+a2z-2+…+anz-n+…+

a2z-2n+2+a1z-2n+1+z-2n

(2) 为保证陷波器只在陷波频率处有效，对其他频率信号无效，传递函数的零极点要相互匹配。即零点位置Pi和极点位置Zi满足如下关系：

Pi=ρ-1Zi,i=1,2,…,n

其中,ρ为陷波带宽的大小。

自适应陷波器能使陷波频率跟随输入信号自动变化。自适应陷波器的传递函数为：

B(z-1)=1+ρa1z-1+ρ2a2z-2+…+ρnanz-n+…+

ρ2n-2a2z-2n+2+ρ2n-1a1z-2n+1+ρ2nz-2n

自适应陷波器的陷波频率为：

因为自适应陷波器计算量小且平、摒弃了小波变换中的基函数选择问题，逐渐广泛的应用于信号分析中固定信号的提取或滤除。

2自适应故障诊断方法

当轴承表面发生多个故障，在滚动体和内环、外环相互作用的运动过程中，形成相互叠加的复合故障。复合故障中不同故障的故障特征频谱结构和时间尺度不同。采用整体频域的分析只能将复合故障信号的特征表达在同一分析过程中，能量小、信号弱的故障特征可能被能量大、信号强的故障特征或噪声信号所淹没。因此，应该尽可能的将复合故障信号特征进行分离，表达在不同的频域后，再通过频谱分析，有针对的提取某一种故障特征。

假设滚动轴承的复合故障由多种典型故障构成，将故障特征最明显，易提取的故障称为主故障；将故障信号较明显，不易提取的故障称为次1故障；将故障信号微弱，不易提取的故障称为次2故障。以此类推，按照故障信号的特征强弱进行逐个命名分析。

利用自适应陷波器的滤波作用，将逐个识别出的故障信号从振动信号中滤除，再进一步分析下一种故障。以达到分离复合故障的目的。归纳为基于陷波器的自适应故障诊断方法，流程图如图1所示。

图1　自适应故障诊断流程图Fig.1 The procedure of adaptive fault diagnosis

首先利用经验模态分解技术(EMD)[19]根据信号的时间尺度特征，将各频段信号分解为由高到低的信号频率成分构成的多个本征模函数。然后将各本征模函数与原始信号进行相关性分析。依据相关系数极值，将噪声信号从采集的振动信号中剔除。得到包含原始信号主要信息的本征模函数，并进行包络谱分析，识别主故障。

将主故障的特征频率及其倍频作为自适应陷波器的陷波频率对轴承振动信号进行滤波。从原采样得到的信号中剔除主故障信息后，再进行频谱分析，识别和诊断次1故障的存在情况。

将识别出的次1故障的特征频率及其倍频作为自适应陷波器的陷波频率对上次陷波后的信号进行滤波。从剔除主故障信息后的原采样信号中又剔除了次1故障信息。再对陷波后的信号进行频谱分析，识别和诊断次2故障的存在情况。

以此类推，利用自适应陷波器对轴承复合故障信号中的已识别故障进行滤波，可以弥补特征明显的故障信号掩盖微弱故障频谱特征的问题，以达到分离复合故障特征，诊断多种故障类型的目的。同时，也避免了小波变换中小波基的选择困难以及EMD正确分解多个混合的多频信号所需要的充分条件问题。

3仿真分析

3.1复合故障信号的仿真

不考虑轴承系统的非线性因素，近似表示轴承系统的复合振动信号如下：

x(t)=x0(t)+xx1(t)+xx2(t)+…

(1)

式中,x0(t)为系统自身的振动信号，可用随机信号描述。xx1(t)、xx2(t)为不同种类故障引起的振动信号。采用冲击信号仿真故障信号[20]，如下式：

xx(t)=dexp(-c(t-Tn))sin(2πf(t-Tn))

Tn=Tn-1+1/Tn=1,2,…

(2)

式中,d为幅值，c为衰减系数，f为固有频率，故障冲击周期为T，Tn为故障冲击发生的时间。

考虑两个不同周期、幅值冲击序列构成的复合故障信号。设第一个故障冲击信号的幅值为20，基频为169 Hz；第二个故障冲击信号的幅值为5，基频为37 Hz。轴承系统自身振动采用幅值为[-30,30]间的随机数表示。复合故障的仿真信号时域图,如图2所示。

图2　复合故障的仿真信号Fig.2 Complex fault signal of simulation

3.2复合故障的诊断

以3.1中的复合故障信号为研究对象，采用自适应复合故障诊断方法进行分析。将复合故障信号进行经验模态分解，得到六个本征模函数IMF1～IMF6，如图3所示。

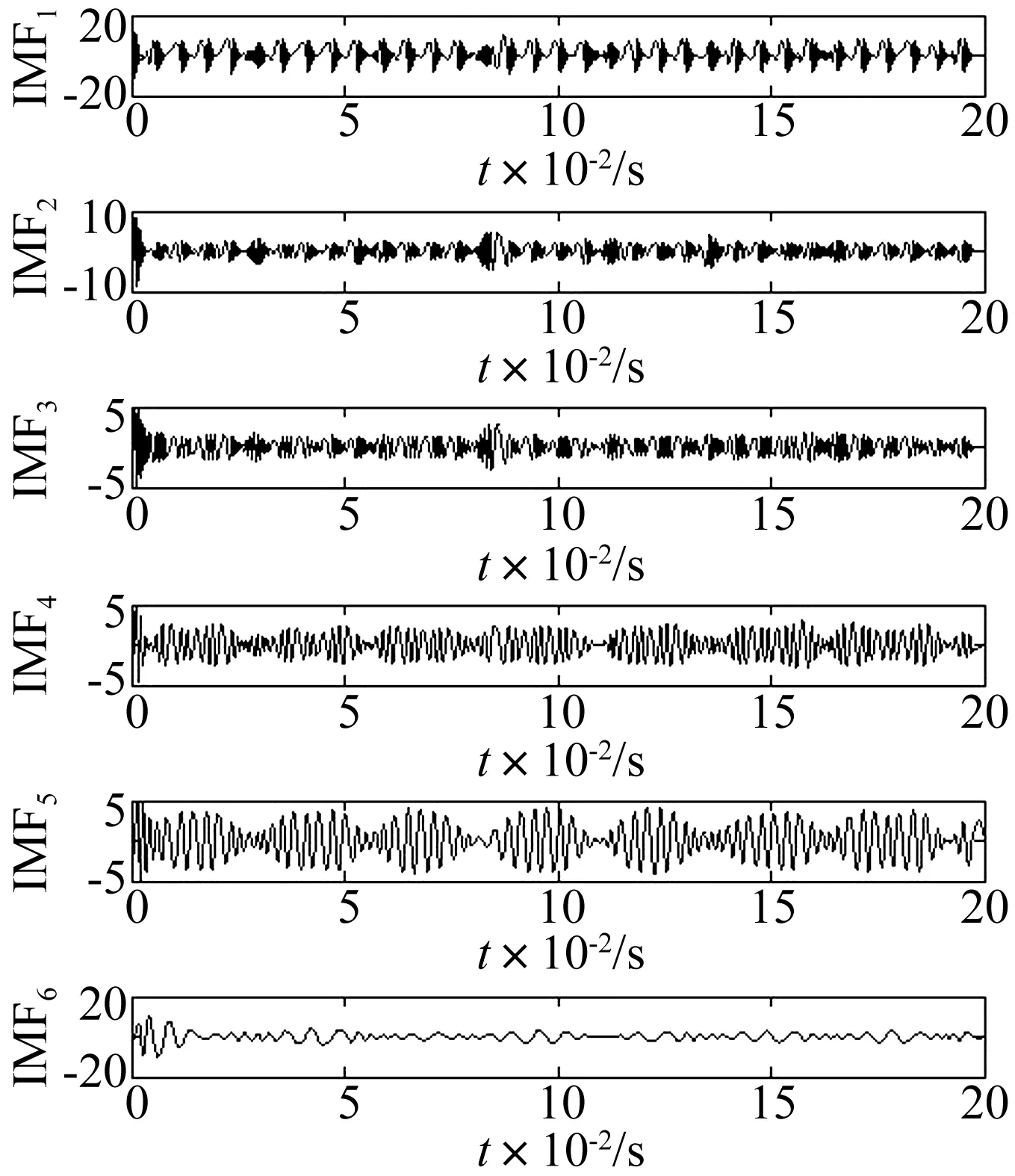
图3　仿真信号的经验模态分解Fig.3 EMD of simulation signal

求各本征模函数与原始仿真信号间的相关系数，如表1所示。

表1　本征模函数与原始仿真信号的相关性

根据相关系数最大化原则，选取IMF1和IMF2对信号进行重构，频谱分析结果如图4所示。从图4中可以找到主故障频率169 Hz及其二倍频338 Hz、三倍频507 Hz。

图4　重构信号的频谱分析Fig.4 Spectrum analysis of denoised signal

以169 Hz及其各倍数为自适应陷波器的陷波频率，对原始仿真信号滤波。滤波后进行包络谱分析，如图5所示。

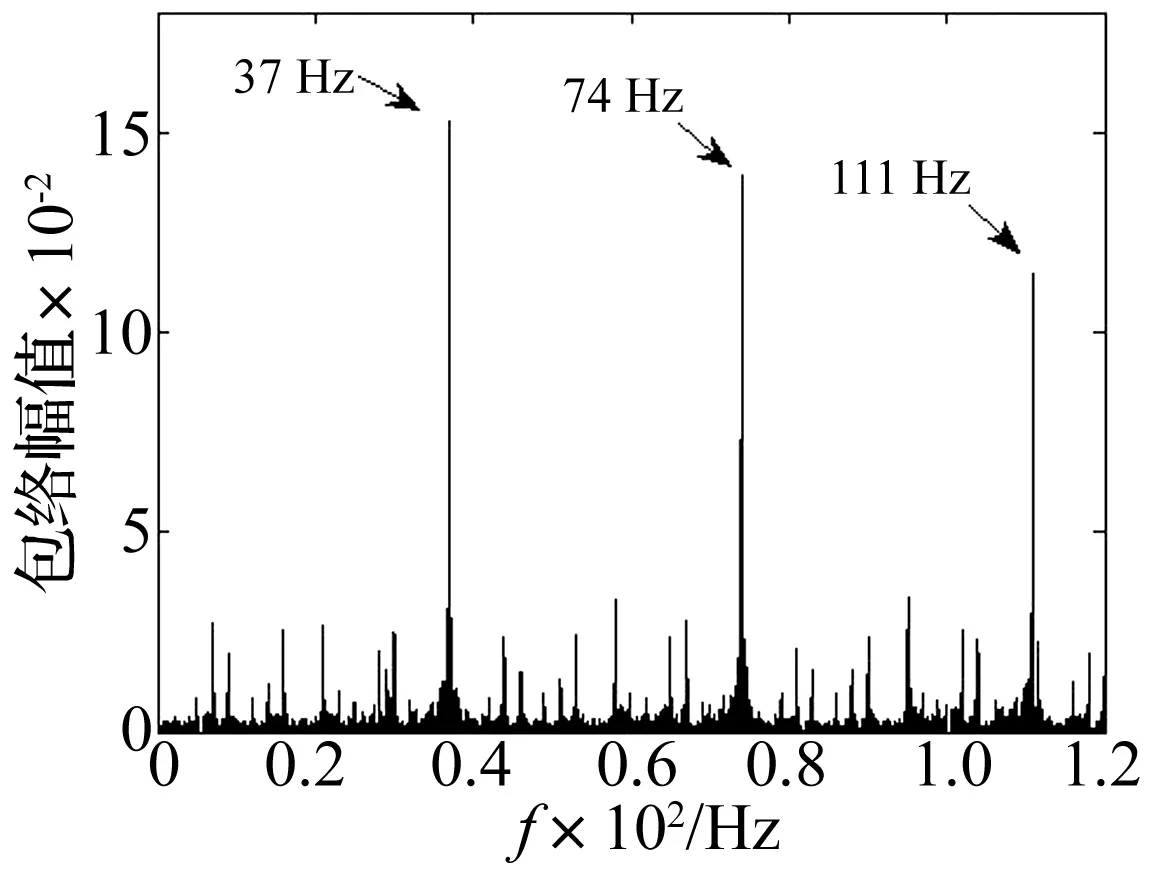
图5　陷波后频谱分析Fig.5 Spectrum analysis after notch filter

从图5中可以清晰的看到次故障频率37 Hz及其二倍频74 Hz、三倍频111 Hz。在识别出主故障后，利用自适应陷波器能够突出次故障的冲击信息，能够较好的检测和诊断出次故障的存在。

4实例验证

4.1实验环境

为了检验自适应复合故障诊断方法的有效性。采用352226X2-RZ型铁路货车轮对滚动轴承为研究对象，通过铁路货车轮对滚动轴承故障诊断实验台进行振动测试实验。所用滚动轴承在实际运行过程中自然产生了严重的外圈剥离和轻微的滚动体电蚀，形成复合故障。

实验过程中，轴承恒定转速为467 r/min，对轴承的加速度振动信号采集，采样频率为5 120 Hz，每次采样点数为102 400，采集数据20组用于检验自适应复合故障诊断方法的有效性。可以通过计算得到外圈故障特征频率为67.327 Hz，滚动体故障特征频率为27.314 Hz。选取其中一组数据进行说明。原始振动信号的局部时域图如图6所示。

图6　复合故障信号局部时域图Fig.6 Complex fault signal in time domain

4.2主故障的诊断

对实验所得振动信号进行经验模态分解，得到各IMF信号如图7所示。

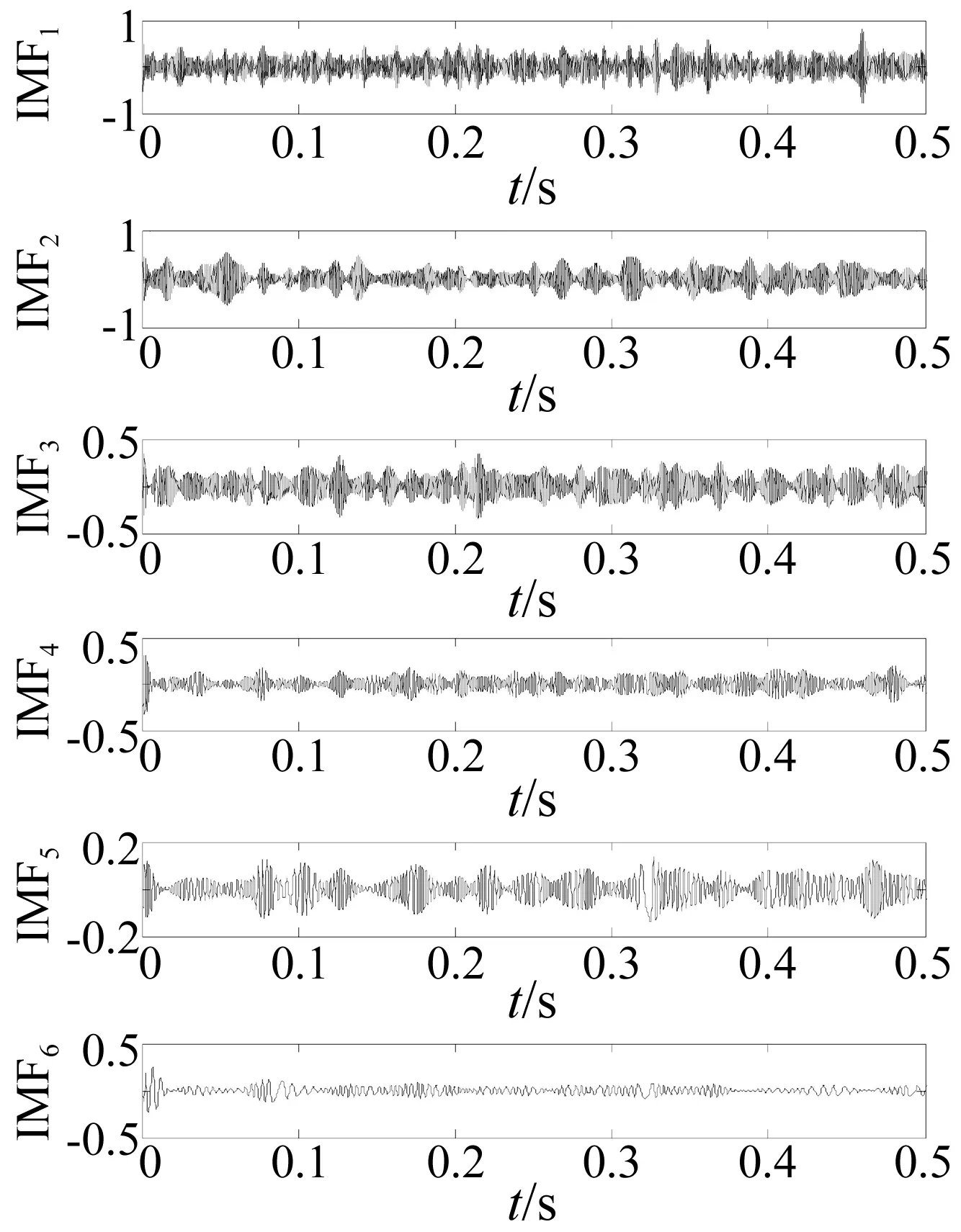
图7　实验信号的经验模态分解Fig.7 EMD of experimental signal

求得各IMF信号与原始实验振动信号之间的相关系数，如表2所示。

表2　 本征模函数与原始实验信号的相关性

根据相关性最大化原则，选取IMF1、IMF3对信号进行重构。对重构后的信号进行包络分析如图8所示。

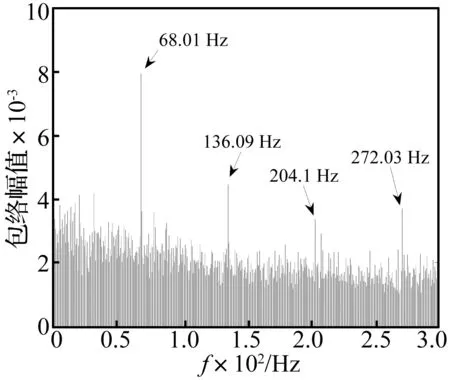
图8　重构信号的频谱分析Fig.8 Spectrum analysis of denosied signal

从图8中可以清晰的看到故障频率68.01 Hz及其各倍频136.09 Hz、204.1 Hz、272.03 Hz。其中68.01 Hz与计算所得外圈故障特征频率相近，可以诊断出滚动轴承存在外圈故障。

4.3陷波器设计

以故障频率及其倍频为陷波器的陷波频率，需要陷波的频率为68.01 Hz、136.09 Hz、204.1 Hz、272.03 Hz……多个频率需要同时进行陷波，采用陷波器串联的形式实现。以陷波器过渡带宽度设计尽量小为原则。陷波器阻带要求在陷波频率的±5 Hz以内。因此各个陷波器的阻带为：

多个陷波器组合形成的滤波特性曲线见图9。

图9　滤波特性曲线Fig 9 Characteristic curve of notch filter

对原始振动信号进行陷波处理。处理后的信号和处理前的信号对比如图10所示。

图10　陷波前后信号对比Fig.10 The contrast of signal before and after notch filters

经过陷波后，68.0 Hz及其倍频处的谱线长度变为0，在[68.0-5，68.0+5]Hz范围内谱线长度均存在一定衰减，其他处的谱线长度不变。实际陷波器的衰减带宽允许陷波频率存在3 Hz误差，因此能够在故障特征频率倍频的正负3 Hz误差范围内进行正确陷波处理。陷波后，基本保留了除主故障及其倍频外的其他频率处的幅频特征。

4.4次故障的识别

对经过陷波后的信号去噪，进行包络谱分析，如图11所示。

图11　次故障诊断Fig.11 Subordinate fault diagnosis

从图中能够找到故障频率27.7 Hz，与计算得到的轴承滚动体故障特征频率接近。可以诊断为滚动轴承存在次故障类型为滚动体故障。

4.5效果分析

(1) 主故障频率的准确性直接影响着次故障的检测结果。如果主故障的识别存在错误，直接导致次故障的分析错误。

(2) 理想陷波器的阻带宽度仅仅限于陷波频率。但实际陷波器的阻带宽度存在一定误差。如果主故障和次故障的频率过于接近，则在利用陷波器滤波时，可能将次故障的特征滤掉。

(3) 陷波器越接近于理想程度，效果越好，但是倍频往往存在误差。因此陷波器的理想度和倍频误差间存在矛盾。

5结论

针对轴承复合故障在单通道检测环境下的分离和诊断困难问题，本文引入了陷波器的思想。在分析复合故障信号特征的基础上，结合比较成熟的经验模态分解方法，提出了基于陷波器的自适应复合故障诊断方法。在分析理想仿真信号后，为了验证算法的可行性，在货车滚动轴承实验台上进行轴承的复合故障振动测试。将自适应复合故障诊断方法应用到复合故障检测中，能够较好地识别出滚动轴承的主故障和次故障的故障类型。从仿真和实验两方面验证了滚动轴承复合故障自适应诊断方法的有效性。

参 考 文 献

[1] 崔玲丽，吴春光，邬娜. 基于EMD与ICA的滚动轴承复合故障诊断[J]. 北京工业大学学报，2014,40(10)：1459-1464.

CUI Ling-li, WU Chun-guang, WU Na.Composite fault diagnosis of rolling bearing based on EMD and ICA algorithm[J]. Journal of Beijing University of Technology, 2014,40(10)：1459-1464.

[2] 唐德尧，王定晓，杨政明，等. 共振解调技术与机车车辆传动装置故障诊断[J]. 电力机车技术，2002,25(5)：1-5.

TANG De-yao, WANG Ding-xiao, YANG Zheng-ming, et al. Demodulated resonance technique and tailure diagnosing of the gearing on the rolling stock[J]. Technology for Electric Locomotives, 2002, 25(5):1-5.

[3] 林京. 连续小波变换及其在滚动轴承故障诊断中的应用[J]. 西安交通大学学报，1999，33(11)：108-110.

LIN Jing. Continuous wavelet transform and its application for bearing diagnosis[J]. Journal of Xi’an Jiaotong University, 1999, 3(11):108-110.

[4] 陈彬强，张周锁，訾艳阳，等. 机械故障诊断的衍生增强离散解析小波分析框架[J]. 机械工程学报，2014,50(17)：77-86.

CHEN Bin-qiang, ZHANG Zhou-suo, ZI Yan-yang, et al. Novel ensemble analytic discrete framelet expansion for machinery fault diagnosis[J]. Journal of Mechanical Engineering, 2014, 50(17):77-86.

[5] Antoni J. The spectral kurtosis: a useful tool for characterising non-stationary signals[J]. Mechanical Systems and Signal Processing, 2006, 20(2):282-307.

[6] 周智，朱永生，张优云，等. 基于EEMD和共振解调的滚动轴承自适应故障诊断[J]. 振动与冲击，2013,32(2)：76-80.

ZHOU Zhi, ZHU Yong-sheng, ZHANG You-yun, et al. Adaptive fault diagnosis of rolling bearings based on EEMD and demodulated resonance[J]. Journal of Vibration and Shock, 2013, 32(2):76-80.

[7] Patel T H, Darpe A K. Coupled bendling-torsional vibration analysis of rotor with rub and crack[J]. Journal of Sound and Vibration, 2009, 326(3/4/5):740-752.

[8] Jalan A K, Mohanty A R. Model based fault diagnosis of a rotor-bearing system for misalignment and unbalance under steady-state condition[J]. Journal of Sound and Vibration, 2009, 327(3/4/5):604-622.

[9] Hong H, Liang M. Separation of fault features from a single-channel mechanical signal mixture using wavelet decompositon[J]. Mechanical Systems and Signal Processing, 2007, 21(5):2025-2040.

[10] Antoni J. Blind separation of vibration components: principles and demonstrations[J]. Mechanical Systems and Signal Processing, 2005, 19(6):1166-1180.

[11] Peled R, Braun S, Zachsenhous A. A blind deconvolution separation of multiple sources with application to bearing diagnostics[J]. Mechanical Systems and Sigtnal Processing, 2005, 19(6):1181-1195.

[12] 沈国际，陶利民，陈仲生. 多频信号经验模态分解的理论研究及应用[J]. 振动工程学报，2005,18(1)：91-94.

SHEN Guo-ji, TAO Li-min, CHEN Zhong-sheng.Theoretical research on empirical mode decomposition of multi-frequency signal and its application[J]. Journal of Vibration Engineering, 2005, 18(1):91-94.

[13] 蔡艳平，李艾华，石林锁，等. 基于EMD与谱峭度的滚动轴承故障检测改进包络谱分析[J]. 振动与冲击，2011,30(2)：167-172.

CAI Yan-ping, LI Ai-hua, SHI Lin-suo, et al.Roller bearing fault detection using improved envelope spectrum analysis based on EMD and spetrum kurtosis[J]. Journal of Vibration and Shock, 2011,30(2):167-172.

[14] 胥永刚，孟志鹏，赵国亮. 基于双树复小波变换的轴承复合故障诊断研究[J]. 仪器仪表学报，2014,35(2)：447-452.

XU Yong-gang, MENG Zhi-peng, ZHAO Guo-liang. Study on compound fault diagnosis of rolling bearing based on dual-tree complex wavelet transform[J]. Chinese Journal of Sicentific Instrument, 2014, 35(2):447-452.

[15] 崔玲丽，高立新，殷海晨，等. 基于第二代小波的复合故障诊断方法研究[J]. 中国机械工程，2009,20(4)：442-446.

CUI Ling-li, GAO Li-xin, YIN Hai-chen, et al.Research on composite fault diagnosis method based on the second generation wavelet[J]. China Mechanical Engineering, 2009, 20(4):442-446.

[16] 张超，陈建军，郭讯. 基于第2代小波和EMMD的转子系统复合故障诊断[J]. 振动、测试与诊断，2011,31(1)：98-103.

ZHANG Chao, CHEN Jian-jun, GUO Xun. Complex fault diagnosis for rotor systems using the second generation wavelet and extremum field mean mode decomposition[J]. Journal of Vibration, Measurement & Diagnosis, 2011,31(1)：98-103.

[17] 储昭碧. 基于自适应陷波滤波器的电力信号时频分析[D]. 合肥:合肥工业大学，2009.

[18] Mojiri M, Karimi-ghartemani M, Bakhshai A. Time-domain signal analysis using adaptive notch filter[J]. IEEE Transactions on Signal process, 2007, 55(1):85-93.

[19] 张志刚，石晓辉，施全，等. 基于改进EMD和谱峭度法滚动轴承故障特征提取[J]. 振动、测试与诊断，2013,33(3)：478-482.

ZHANG Zhi-gang, SHI Xiao-hui, SHI Quan, et al. Fault feature extraction of rolling element bearing based on improved EMD and spectral kurtosis[J]. Journal of Vibration, Measurement & Diagnosis,2013, 33(3)：478-482.

[20] 明安波，褚福磊，张炜. 滚动轴承复合故障特征分离的小波-频谱自相关方法[J]. 机械工程学报，2013,49(3)：80-87.

MING An-bo,CHU Fu-lei, ZHANG Wei. Compound fault features separation of rolling element bearing based on the wavelet decomposition and spectrum auto-correlation[J]. Journal of Mechanical Engineering, 2013, 49(3): 80-87.

Adaptive compound fault diagnosis of rolling bearings

MA Xin-na1, YANG Shao-pu2

(1. School of Information Science and Technology, Shijiazhuang Tiedao University, Shijiazhuang 050043, China;2. College of Mechanical Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China)

Abstract:In the process of bearing inspection of freight cars, compound faults are prevalent. Aiming at improving the difficulty of separating the compound fault features from a single-channel vibration signal, an adaptive fault diagnosis method based on notch filter was proposed. The original compound fault vibration signals were decomposed by using the empirical mode decomposition (EMD). Then the vibration signals were reconstructed in accordance with the principle of maximum correlation coefficients between the intrinsic mode functions (IMFS) and the original signal and the spectrum analysis was utilized to identify the primary fault. Then, the primary fault signal was filtered out from the original signal with the adaptive notch filter system, and subordinate faults were diagnosed through the filtered signal. The results of simulation and experimental signals indicate that the adaptive fault diagnosis method based on notch filer can extract the features of primary and subordinate faults from compound fault signals and is valuable for engineering application.

Key words:compound fault; rolling bearing; notch filter; empirical mode decomposition

基金项目：国家自然基金项目(11372197;11227201)；河北省自然基金项目(E2014210078)

收稿日期：2015-04-02修改稿收到日期：2015-06-19

中图分类号:TP391.9; TH133.33

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.10.023

第一作者 马新娜 女，博士，副教授，1978年生