磁流变减振器高频硬化特性建模及优化

左曙光， 毛　钰， 吴旭东， 蒋维旭， 韦锡晋

(同济大学 新能源汽车工程中心，上海　201804)

磁流变减振器高频硬化特性建模及优化

左曙光， 毛钰， 吴旭东， 蒋维旭， 韦锡晋

(同济大学 新能源汽车工程中心，上海201804)

摘要：为准确反映磁流变减振器(MRD)的高频输出特性，基于考虑液体流动惯性和可压缩性的基本磁流变减振器模型，结合高频情况下的MRD内部流动特征，引入流动局部损失成分并考虑磁流变减振器液室内压力分布规律提出了修正的高频模型。为验证模型的准确性，采用动态分层的动网格方法进行了在活塞高频往复运动下磁流变液室内流动情况的计算流体力学(CFD)仿真并获得阻尼力输出。仿真结果表明，提出的模型能够反映磁流变减振器的高频动态硬化情况并准确地预测高频特性曲线中峰值对应频率和峰值大小。最后基于修正的理论模型在保证低频使用性能的前提下以改善高频动态硬化为目标对MRD结构参数进行了优化设计，改善了其高频硬化特性，为MRD的应用和设计提供了参考。

关键词：磁流变减振器(MRD)；高频硬化；压力分布；CFD；结构优化

磁流变减振器作为一种阻尼连续可调的阻尼器具有响应迅速(ms级)、所需能耗低(5 V，2 A)、阻尼调节范围大等优势[1]，因其在低频工作环境下可以实现在共振频率附近处的大阻尼，并且在其他频段有较大的阻尼调节范围以获得较为突出的减振效果，在针对中低频率范围内(30 Hz以内)的隔振场合得到了广泛的应用[2-5]。近几年，随着研究的深入，磁流变减振器的应用场合得到了极大的拓展，如在航空航天、船舶潜艇、轮毂电机驱动电动汽车悬架系统以及发动机悬置等领域，在这些工作环境下存在比较复杂和宽频的外界激励，对于磁流变减振器的性能要求更高，但其中高频动态硬化特性的存在也影响了其使用性能。因此为更好地满足磁流变减振器用以衰减宽频振动激励的需求，对磁流变减振器的高频动态特性展开研究成为必要。

Pierrick等[6]考虑将磁流变减振器应用于火箭发射中卫星的半主动隔振系统并进行了六角隔振装置模拟试验研究，结果表明在宽频激励下，磁流变减振器的隔振性能衰减，对高频激励响应较慢。张步云等[7]在自由悬挂的铝制圆筒梁两端安装磁流变减振器研究其隔振性能，发现磁流变减振器在低频段具有良好的隔振性能，在80 Hz以上基本丧失阻尼可控性，而在235 Hz以上的高频段隔振效果不明显。Brigley等[8]在分析磁流变液常见的三种工作模式时指出流动模式的隔振器在受到高频小振幅激励时，在两个磁极间隙间会产生动态硬化现象，磁流变液将不再发生流动。上述研究从试验现象的角度揭示了磁流变减振器运用于高频隔振场合存在的动态硬化现象及其具体表现，为减振器高频隔振性能的研究了提供基础和参考。但文献对于该现象的深层次机理缺乏探究，未能从理论的角度给出动态硬化的描述并给出结构设计改进的指导意见。

涂奉臣等[9-10]分析了磁流变减振器的高频动刚度硬化产生的机理并在考虑流动惯性的基础上建立了相应的集总参数模型。Alexander等[11]考虑液体可压缩性和流动惯性建立了类似于质量弹簧阻尼系统的高频零场磁流变减振器模型。Gololasz[12]在其基础上提出了多个上述质量弹簧阻尼单元串联的液压网络模型并通过CFD仿真进行验证。对比分析表明：随着液压单元个数的增加，模型与CFD结果接近程度提高，但阻尼力频率曲线峰值处的阻尼力和对应的频率还是存在明显的误差。上述文献基于简单流动机理所建立高频模型在一定程度上反映了高频动态硬化，但由于对减振器内部一些高频流动现象(如局部损失，液室压力不均匀分布等)的简化，模型分析结果与试验或有限元仿真结果之间存在明显误差，模型准确性有待于提高。在高频动态硬化现象的优化改进的研究方面，Zhu等[13]提出了一种新型的磁流变流体挤压油膜阻尼器，利用较低的磁流变液初始黏度和较大的活塞与阻尼器的径向间隙以缓解阻尼器的高频动态硬化。Sung等[14]设计制造了一个具有混合工作模式的磁流变减振器，将线圈分布在活塞的左右两侧进行缠绕，通过对比发现在输出同样阻尼力的情况下，动态硬化现象得到了缓解。Brigley等[8]利用弹性体和活塞杆串联并且采用多种模式并用的结构，得到了一个可以缓解动态硬化，并且在动态硬化后可以利用弹性体提供较小的动刚度的减振器结构。上述改进方案多是根据定性的设计准则从结构布置形式的改进角度对减振器进行优化，使结构变动较大。

因此，本文将考虑流动的局部损失和液室内压力分布建立能够准确反映高频动态硬化的理论模型，并通过在FLUENT中仿真验证模型预测高频阻尼力的准确度，最后基于理论模型在保证低频使用性能的前提以改善高频动态硬化为目标对磁流变减振器结构参数进行了优化设计。

1磁流变减振器高频模型

1.1磁流变减振器结构简化

不同于传统的液压减振器，磁流变减振器不存在复杂的阀结构，节流作用仅来自于中间的环形孔口，典型的磁流变减振器结构如图1所示，对于一些非圆环型液流间隙结构本文的模型可以类推。环形通道沟通了压缩腔和扩张腔，随着活塞的往复运动，两液室(即压缩腔和扩张腔)体积发生变化，使得流体流经环形通道。氮气填充的储能器主要作用是针对单杆式结构补偿由于活塞杆引起的液室体积变化，关于氮气的影响可按理想气体的绝热过程计算气体压力变化并折算成阻尼力，因此在建模时将活塞杆和储能室一并不予考虑，将模型简化为如图2所示，由两液室、环形通道和往复运动的活塞组成。

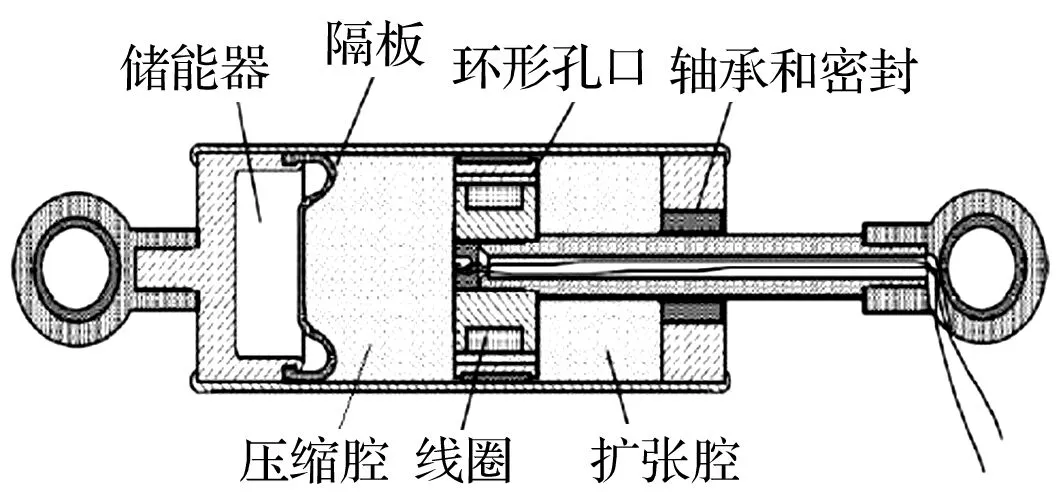
图1　磁流变减振器Fig.1 MR damper

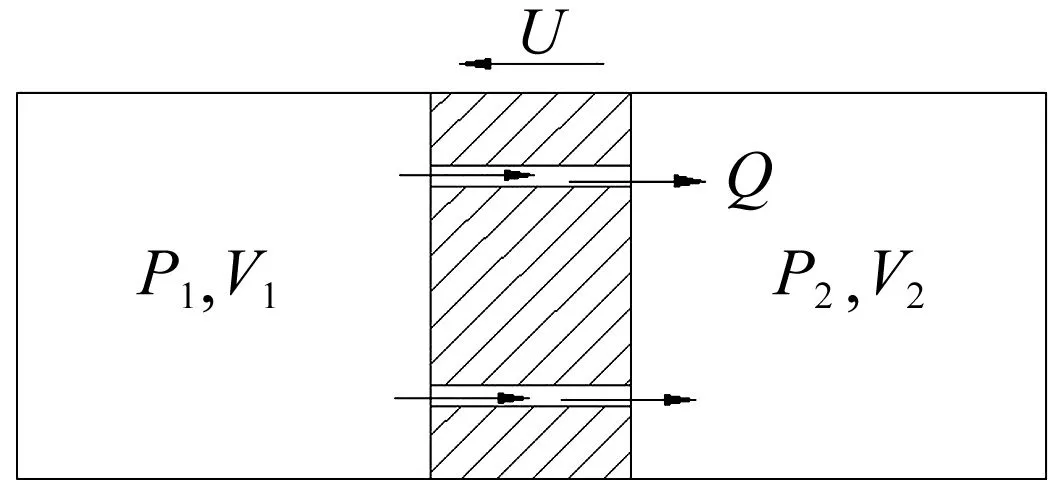
图2　磁流变减振器结构简图Fig.2 Structure diagram of MR damper

1.2磁流变减振器高频特性模型

液体的可压缩性和流动惯性对减振器高频输出特性有较大的影响，在此参照文献[11]建立集总参数模型。假定① 通道内流动为充分发展层流；② 压缩腔(扩张腔)内压力一致，不随轴向位置发生变化。由流动的连续性方程和动量方程得(对非圆环型液流间隙结构按其相应结构修改沿程水力损失即可，具体可参考文献[15]：190-191)

(1)

式中ρ、η、β分别为磁流变液密度、动力黏度和体积模量，hg、Lg、Ag为环形通道间隙、长度和面积，L、Ap为液室长度和面积，V1、V2为左、右液室体积，P1、P2为左、右液室压力，hL为沿程水力损失，ΔPη为通道沿程损失压降，U为活塞运动速度，Q为通道内流量，g为重力加速度，F为输出阻尼力。

1.3考虑局部损失的模型修正

在上述推导中假设间隙通道处流动为充分发展层流，而实际上环形通道入口与出口两端处流通截面面积有突变，在附近会引起复杂流动。

图3为有限元仿真得到的减振器内局部流动速度矢量图，从中可以看出在通道末端存在较强的涡流。涡流的运动会消耗能量造成流体在液室内的流动损失，从而改变通道两端压降并进而影响阻尼力输出。为体现这一影响需在模型动量方程中引入涡流损耗带来的压降项。该减振器内部涡流源于流通截面的突变，可按局部损失处理。

图3　减振器中局部流动速度矢量图Fig.3 Local flow velocity vector diagram in a damper

由流体力学相关理论[15]可确定管道截面突然扩大或缩小情况下的局部水力损失。在减振器活塞运动过程中两种情况都存在，所以由局部损失引起的压降为

(2)

式中hj1为突扩管局部水力损失，hj2为突缩管局部水力损失，ΔPj为局部损失引起的通道两端压降，其余参数与式(1)中一致。考虑局部损失后则式(1)中动量方程修正如下

(3)

1.4考虑压力分布的模型修正

在上述两模型中，均假定两液室内压力不随位置发生变化，而在减振器实际工作过程中在两液室内也存在较为复杂的流动，因此压力是随位置而变化的。下面将基于流体力学基本方程推导液室内压力的分布情况。

图4　液室内流体微元分析图Fig.4 Fluid infinitesimal analysis diagram

对流体微元运用动量方程和连续性方程得

(4)

(5)

式中ω为活塞运动频率，p1、p2为待定系数，由边界条件x=0处为刚性壁面，即Q= 0得p1=p2。令移动边界x=L处的压力为P1(t)。则压缩腔中的压力p(x,t)为

(6)

根据体积弹性模量的定义式可积分得到密度与压力的关系

(7)

对整个压缩腔运用质量守恒方程得

(8)

式中W为活塞运动位移。联立式(6)～式(8)得

(9)

同理对扩张腔进行分析可得

(10)

相应地修正式(1)中的第3、4个表达式得到在引入局部损失的模型中考虑液室内压力分布的模型为

(11)

2模型验证分析

2.1CFD建模仿真

为验证所提出模型相对之前模型的精度，在FLUENT中进行CFD仿真计算磁流变减振器在活塞往复运动下的阻尼力。根据某商用磁流变减振器(RD-8041-1)结构形式进行结构简化确定用于仿真的结构如图5所示，相关尺寸参数及磁流变液材料属性参数见表1。

图5　减振器结构示意图Fig.5 Fluid infinitesimal analysis diagram

同样在有限元分析中考虑磁流变液的可压缩性，通过用户自定义函数按式(7)设置液体的密度随压力变化以反映磁流变液的可压缩性。采用动态分层网格更新算法实现动网格以模拟活塞的往复运动，指定其往复运动的速度是幅值为0.3 m/s，频率取值为0～450 Hz的余弦函数。在活塞表面对压力进行积分得到输出阻尼力大小。

表1　参数值

2.2模型对比验证分析

根据表1中的参数值进行模型仿真和有限元仿真，仿真结果对比见图6(其中模型一为基本高频动态特性模型，模型二为引入局部损失后的模型，模型三为考虑局部损失和压力分布的最终修正模型)。

从图6可以看出在活塞运动频率为200 Hz时，文中的三个模型与有限元结果都吻合较好：① 稳定后，模型与有限元仿真所得阻尼力的时域曲线均为频率200 Hz的正(余)弦曲线，且二者同时达到峰值和经过零点，说明模型能够正确的反映输出阻尼力的相位及相对活塞速度输入的滞后；② 在幅值方面模型与有限元结果也比较接近，模型能准确预测阻尼力水平。

但在图7中，当活塞运动频率增加到340 Hz时，三个模型与有限元结果的接近程度有所不同，其中模型三(即本文所提出的考虑局部损失和压力分布的模型)在幅值上与有限元结果相近程度最好。

实际上，在频率为340 Hz时，模型三种的修正系数cm=1.129与200 Hz时的cm=1.040 5相比有较明显的增加，突显出了模型三在考虑压力分布后的不同，可以推断随着频率的进一步增加，模型三的优势也将更加明显。

图6　频率为200 Hz激励下有限元与三个模型的阻尼力时域结果对比Fig.6 Time domain comparison between damp forces of three models in 200 Hz

为更直观地比较三个模型，在图8中给出了各模型与有限元在不同频率下，阻尼力幅值对比情况。从中可以看出：① 三个模型中在频率达到某一值后，阻尼力随频率增加较快，并出现了峰值，体现了减振器的高频动态硬化，这是由液体的可压缩性和流动惯性引起的。② 修正后的模型在预测减振器高频特性曲线峰值对应频率的误差由11%降为0.8%，峰值大小误差由35.4%降为9.6%(见表2)，模型准确度得到大幅提高,能准确反映磁流变减振器的高频动态特性，可用于后续优化分析。

图8　阻尼力频率特性Fig.8 Frequency characteristics of damping force

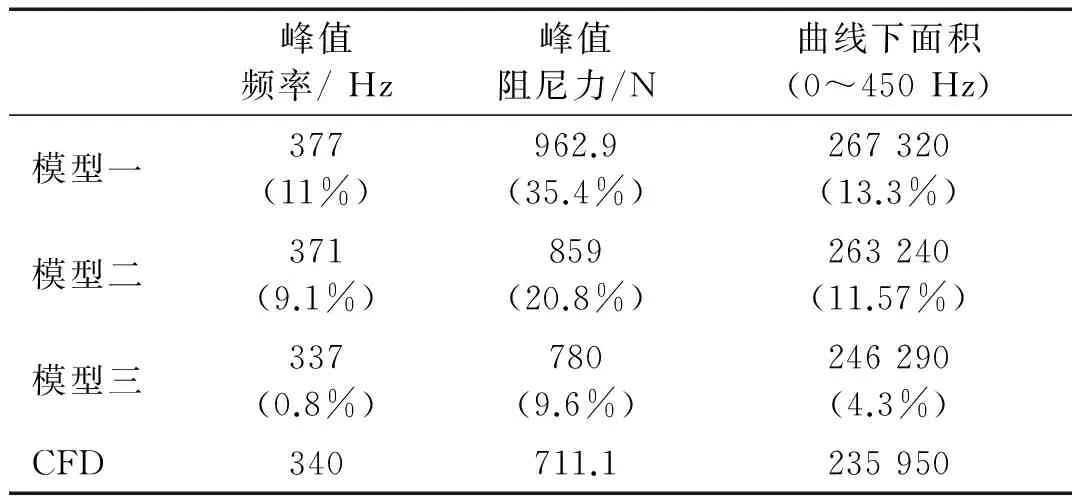
峰值频率/Hz峰值阻尼力/N曲线下面积(0～450Hz)模型一377(11%)962.9(35.4%)267320(13.3%)模型二371(9.1%)859(20.8%)263240(11.57%)模型三337(0.8%)780(9.6%)246290(4.3%)CFD340711.1235950

注：括号内为模型相对CFD的误差

3高频特性优化分析

为满足高频隔振性能，磁流变减振器高频激励下需要保持较小的阻尼力输出，而高频动态硬化现象使得磁流变减振器的输出阻尼力随频率增加明显。故本文以缓解高频动态硬化为目标对减振器结构进行优化分析。

3.1优化条件设置

在改善磁流变减振器的高频动态特性时还需要保证磁流变减振器在低频的使用性能，涉及的优化目标、优化参数和约束条件复杂，故采用多岛遗传算法为优化方法。

隔振元件的动态特性一般由动刚度反映，动刚度定义为由位移输入到力输出的传递函数，即Kd(ω)=F(ω)/W(ω),对于减振器F(ω)为单频阻尼力幅值，W(ω)为活塞单频位移幅值，ω为频率，通过给定不同频率的活塞位移激励求解阻尼力可确定动刚度随频率变化关系。另外为突显出的硬化程度并同时考虑到磁流变减振器的高频硬化主要来源于液体的可压缩性和流动惯性，定义磁流变减振器实际动刚度与忽略可压缩性和流动惯性得到的动刚度之比作为动态硬化系数，即η(ω)=Kd(ω)/Kl(ω)，Kd(ω)为减振器实际动刚度，Kl(ω)为只考虑黏滞损失的理想减振器动刚度；动刚度和硬化系数随频率变化曲线直观地反映了减振器的高频使用性能。因此将其量化选择动刚度曲线面积以及硬化系数曲线面积作为优化目标。

在低频工作条件下，磁流变减振器需施加电流控制产生磁场以激活磁流变液，从而提供较大阻尼力衰减系统的振动，为此磁流变减振器应同时满足磁路设计的要求。磁路设计要求磁路中各部分不先于阻尼通道内磁流变液达到磁饱和[16]，故以此为原则确定约束条件，其实现方法如图9：由磁路中各部分磁通量相等确定阻尼通道达到饱和时其他磁路部分的磁感应强度，并与材料的饱和磁感应强度进行对比以判断磁路各部分的饱和情况，未达到饱和即满足上述原则继续优化，否则返回继续。

图9　非线性约束流程图Fig.9 The flow chart of nonlinear constraints

考虑磁流变减振器中主要影响流动和磁路的结构，选取优化变量如表3所示(表中涉及符号见图5)

表3　优化变量及其取值

3.2优化结果分析

图10、11为优化前后动刚度和硬化系数的对比曲线，从图10中可以看到，优化后的结构参数能有效地减小共振频率380 Hz附近的动刚度，在400 Hz，优化后的动刚度减小的幅值达到了37.9%。而在30～150 Hz的频率范围内，优化后的动刚度稍大于优化前的动刚度，对30 Hz以下的动刚度几乎无影响，因此对于150 Hz以内的阻尼力输出特性影响不大。从图11可以发现，磁流变减振器的高频动态硬化系数也得到了显著的优化。优化前的硬化系数在400 Hz达到了1.55，而优化后的硬化系数为1.28，减小了近17.42%，有效地缓解了磁流变减振器的高频动态硬化现象。另外计算优化后磁流变减振器通以允许最大电流时磁路中各部分磁感应强度，其中铁芯处磁密最大为1.247 08 T，小于铁芯材料电工纯铁的饱和磁密，满足低频使用性能要求。表4为优化前后变量的变化量，从中可以看出关键结构尺寸的变动不超过20%，与文献中提到的结构布置形式改进的方案相比本文的方法能够有效地降低设计开发成本。

表4　变量优化前后对比

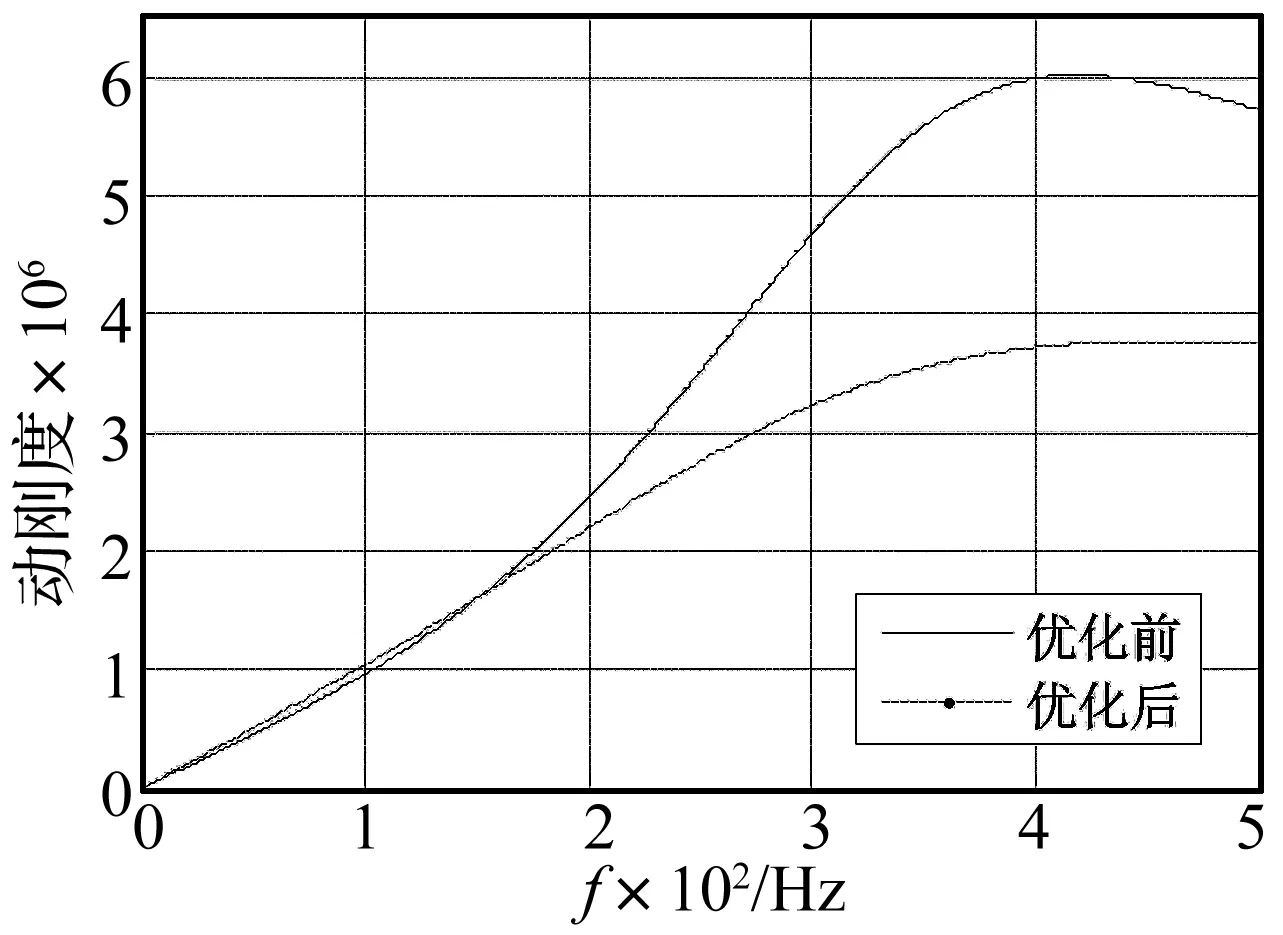
图10　优化前后动刚度对比Fig.10 Comparison of dynamic stiffness before and after optimization

图11　优化前后硬化系数对比Fig.11 Comparison of hardening coefficient before and after optimization

4结论

本文建立了磁流变减振器的高频动态模型，并与CFD仿真对比表明：考虑了液室压力分布和流动局部损失的修正模型，能更准确地预测减振器高频特性曲线峰值大小及其对应频率，验证了本文根据局部损失和液室压力分布进行模型修正的必要性和正确性。基于修正模型以改善高频动态硬化为目标进行优化设计表明：通过减振器结构尺寸的合理选择能够使硬化程度显著降低，而关键尺寸的变动不大，相对于之前文献中提到的结构布置形式的改动能有效节省设计开发成本。本文的建模和优化方法有效地针对磁流变减振器存在的高频动态硬化问题进行了研究和改善，为磁流变减振器的动态特性深入分析、选型和设计提供了参考，拓展了磁流变减振器在高频隔振场合的应用。

参 考 文 献

[1] 王琪民,徐国梁,金建峰.磁流变液的流变性能及其工程应用[J]. 中国机械工程, 2002,13(3):93-96.

WANG Qi-min, XU Guo-liang, JIN Jian-feng. The rheological property and engineering application of magnetorheological fluids[J]. China Mechanical Engineering, 2002,13(3):93-96.

[2] Carlson J D, Catanzarite D M, St Clair K A. Commercial magneto-rheological fluid devices[J]. International Journal of Modern Physics B, 1996, 10(23/24):2857-2865.

[3] Yang G, Spencer B F, Carlson J D, et al. Large-scale MR fluid dampers: modeling and dynamic performance considerations[J]. Engineering structures, 2002, 24(3):309-323.

[4] Ha S H, Seong M, Choi S. Design and vibration control of military vehicle suspension system using magnetorheological damper and disc spring[J]. Smart Materials and Structures, 2013, 22(6):65006.

[5] Gordaninejad F, Kelso S P. Magneto-rheological fluid shock absorbers for HMMWV[C]// SPIE’s 7th Annual International Symposium on Smart Structures and Materials. International Society for Optics and Photonics. Newport Beach, CA, 2000: 266-273.

[6] Pierrick J, Ohayon R, Le Bihan D. Semi-active control using magnetorheological dampers for payload launch vibration isolation[C]//Smart Structures and Materials, 2006 International Society for Optics and Photonics. San Diego, CA,2006.

[7] 张步云, 陈怀海, 贺旭东, 等. 磁流变阻尼器减振特性实验研究[J]. 南京航空航天大学学报, 2013,44(6): 855-861.

ZHANG Bu-yun, CHEN Huai-hai, HE Xu-dong, et al. Experiment study on damping characteristic of magneto-rheological damper[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2013, 44(6): 855-861.

[8] Brigley M, Choi Y T, Wereley N M, et al. Magnetorheological isolators using multiple fluid modes[J]. Journal of Intelligent Material Systems and Structures, 2007, 18(12): 1143-1148.

[9] 涂奉臣, 陈照波, 李华, 等. 新型整星隔振平台的被动隔振性能及星箭耦合特性分析[J]. 航空学报,2010,31(3):538-545.

TU Feng-chen, CHEN Zhao-bo, LI Hua, et al. Research on passive isolation characteristics and rocket-spacecraft coupling of a new whole-spacecraft isolation platform[J]. Journal of Aeronautics, 2010, 31(3): 538-545.

[10] 涂奉臣. 基于磁流变阻尼器的整星半主动隔振技术研究[D]. 哈尔滨:哈尔滨工业大学, 2010.

[11] Alexandridis A, Go dasz J. Simplified model of the dynamics of magneto-rheological dampers[J]. Mechanics,2005,24(2):47-53.

[12] Goldasz J. High-frequency model of monotube shock absorbers[J]. Modelowanie Inžynierskie, 2010, 8: 81-88.

[13] Zhu Chang-sheng. Dynamics of a rotor supported on magneto-rheological fluid squeeze film damper[J]. Chinese Journal of Aeronautics, 2001, 14(1): 6-12.

[14] Sung K G, Choi S B, Lee H G, et al. Performance comparison of MR dampers with three different working modes: shear, flow and mixed mode[J]. International Journal of Modern Physics B, 2005, 19(7/8/9): 1556-1562.

[15] 景思睿. 流体力学[M]. 西安: 西安交通大学出版社,2010.

[16] 潘杰锋. 磁流变减振器结构设计及优化[D]. 重庆:重庆大学, 2010.

Modelling and optimization of high frequency hardening characteristics of magneto rheological damper

ZUO Shu-guang, MAO Yu, WU Xu-dong, JIANG Wei-xu, WEI Xi-jin

(Clean Energy Automotive Engineering Center, Tongji University, Shanghai 201804, China)

Abstract:In order to reflect high-frequency characteristics of magneto rheological damper(MRD) exactly, based on the model of MRD considering inertia and compressibility, a modified high-frequency model was proposed in which the local loss of flow was introduced and the pressure distribution in the liquid chamber of MRD was taken into consideration as well. To verify the accuracy of the model, a CFD simulation of the flow in MRD by using dynamic layering algorithm to achieve dynamic meshing was performed. The simulation results indicate: the model proposed is able to reflect the dynamic hardening of MRD in high frequency domain and predict the peak value and its corresponding frequency on the high frequency characteristic curve more accurately. Based on the model, the structural parameters of MRD were optimized aiming to improve the dynamic hardening under the prerequisite of ensuring low frequency performance, which provides references to the design and analysis of MRD in high frequency domain applications.

Key words:MR damper; high frequency hardening; pressure distribution; computational fluid dynamics (CFD); structure improvement

基金项目：国家自然科学基金资助项目(51375343)；上海市教委科研创新项目(15ZZ015)

收稿日期：2015-04-14修改稿收到日期：2015-05-22

通信作者吴旭东 男，博士，助理教授，1983年生

中图分类号:TH137；U463.3

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.10.019

第一作者 左曙光 男，博士，教授，博士生导师，1968年生

E-mail:wuxudong@tongji.edu.cn