框架结构瞬态波动响应及自振频率的回传射线矩阵法分析

陈进浩， 余云燕

(兰州交通大学 土木工程学院，兰州　730070)

框架结构瞬态波动响应及自振频率的回传射线矩阵法分析

陈进浩， 余云燕

(兰州交通大学 土木工程学院，兰州730070)

摘要：基于回传射线矩阵法，通过节点的力平衡和位移协调条件及局部坐标系下单元两端位移之间的关系，建立方波脉冲激振力作用下铰接T形框架的回传射线矩阵。在此基础上分析了弹性波在框架中的传播特征，探讨了单元交界点处的反射波、入射波与透射波的波形特征。以回传射线矩阵法为基础，求解此框架的自振频率，并与有限元法求出的结果进行比较，结果表明，二者之间的结果非常接近，以此证明了该方法的有效性。

关键词：回传射线矩阵法；弹性波；框架结构；自振频率

结构在建造和正常使用过程中，除了受到静力荷载外，还会受到各种各样的冲击荷载。由于冲击荷载作用时间极短，在以毫秒(ms)、微秒(us)乃至纳秒(ns)为计的短暂时间内，结构受力及位移发生较为显著变化，用一般力学方法难以解决。而波动理论则为解决此类问题提供一条有效途径。

多年以来，波动理论在固体力学领域一直是一个应用较为广泛的理论。在现代工程技术中越来越受到人们的重视。在地质勘探、地震预测、高速撞击、爆炸、结构的无损检测、应力波探伤和有缺陷结构的探测等领域，波动理论得到了广泛的应用。许多专家和学者对此类问题进行了深入的研究。

针对冲击荷载作用下结构的瞬态响应问题，Howard等[1-2]首先基于Timoshenko梁理论提出了回传射线矩阵法的波动模型；余云燕等[3-7]应用该方法研究了埋置框架结构及有损伤框架结构中的波动响应；田家勇等[8]应用该方法在引入节点质量阻尼模型后对刚架结构进行减振分析；严蔚等[9]结合压电阻抗技术对含裂缝智能梁的振动特性进行了研究。黄锦雄等[10]应用该方法进行了深水油井套管柱的地震响应分析。郭永强等[11-13]应用该方法进行了结构的自振特性研究。本文基于回传射线矩阵法分析了弹性波在框架中的传播特征，结构单元交界点处位移协调条件及受力平衡条件的波形特征，以单元节点处的位移协调条件为基础得到了弹性波在每次传至单元交界点处的入射波、反射波及透射波的波动表达式及波形特征。之后用该方法求得了结构的自振频率并与ANSYS和SAP2000求得的结果进行对比，以验证该方法的有效性。

1回传射线矩阵法的基本原理

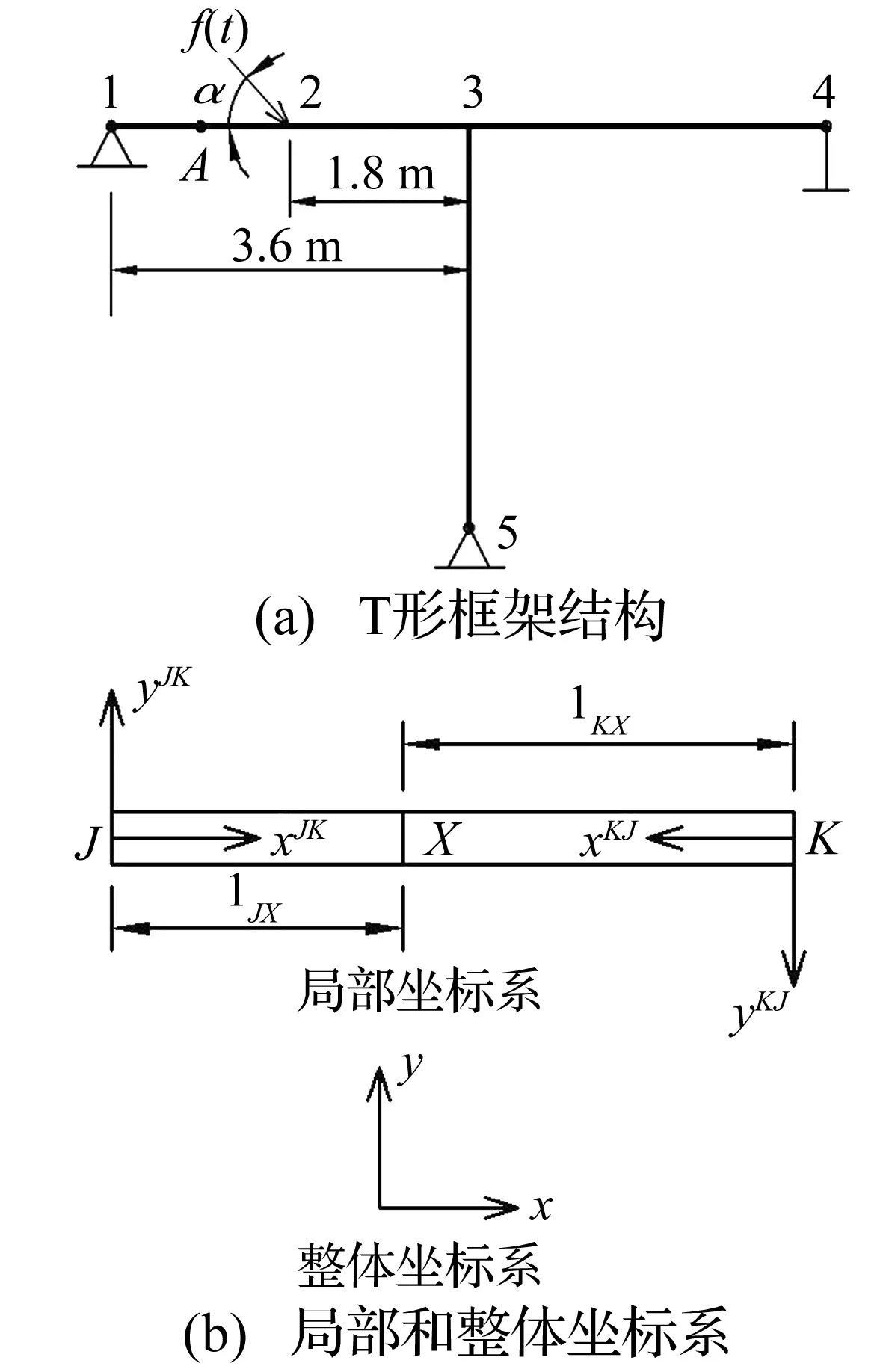
图1　T形框架结构与结构坐标系Fig.1 T-shaped frame and coordinate

框架结构如图1所示，假设结构各单元具有相同截面和材料特性。E为材料弹性模量，G为剪切模量，ρ为密度，A为横截面积，μ为泊松比，杆件13、34、35长度都相等，其中2点为13的中点。在节点2上作用有与水平方向成α角的方波脉冲激振力。

(1)

式中：u为轴向位移，υ=υb+υs为挠度。其中，υb为弯矩引起的挠度，υs为剪力引起的挠度，κ′为截面剪力系数。

将上式进行Fourier变换后，在频域中对各节点建立局部坐标系下的力平衡及位移协调条件关系式，整理后可得：

dj=Sjaj+sj

(2)

式中，aj和dj表示j点入射波和出射波波幅向量，Sj为

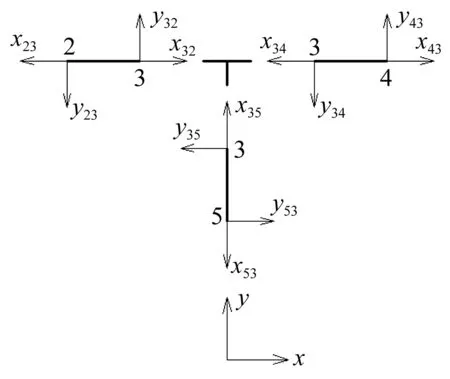
图2　节点3处的局部与整体坐标系Fig.2 Local and global coordinate system at joint 3

j点的局部散射矩阵，sj为j点的波源矢量(外荷载列向量)。对本文所研究的结构，只有节点2处有可分解为水平和竖直方向的外荷载，故除节点2之外，其余节点处的波源矢量都为零矢量。每个节点处有三个自由度。节点1、4、5只连接一个单元，节点2连接两个单元，节点3连接三个单元。故S1、S4、S5都是三阶方阵，S2是六阶方阵，S3是九阶方阵。以节点3为例，与节点3连接的各单元的局部与整体坐标系如图2所示。

频域中节点3处的位移协调及力平衡条件为：

(3a)

对式(3a)整理并合并为：

d3(ω)=S3(ω)a3(ω)+s3(ω)

(3b)

式中，a3和d3表示节点3处局部坐标系下的入射波和出射波波幅向量，S3和s3分别为节点3处的局部散射矩阵和波源矢量：

d3=[d132,d232,d332,d134,d234,d334,d135,d235,d335]T

a3=[a132,a232,a332,a134,a234,a334,a135,a235,a335]T

s3=[000000000]T

将所有节点的a、d、S、s组集到整体坐标系中，写成紧凑形式为：

d=Sa+s

(3)

式中S称为整体散射矩阵。

图1所示的局部坐标系中，考虑到单元两端点处的位移协调条件，引入传播矩阵PKJ，得到表示出射波波幅和入射波波幅之间的相位关系式：

(4)

a=PUd

(5)

将式(5)代入式(4)，有：

d=[I-R]-1s

(6)

式中，R=SPU，称为回传射线矩阵。

结构受到扰动离开平衡位置后不再受任何外力影响的振动过程称为自振，此时的振动频率为自振频率。当结构的振动频率等于其自振频率ωn时有：

[I-R]d=0

(7)

R中的各项是关于频率ω的复数表达式。在数学上没有求解此类方程的方法，为求得式(7)的解，可利用数值计算方法中求解极小值的黄金分割法求得零点位置。

由于自振频率的存在。方阵存在奇异点,在奇异点处逆矩阵不存在。为解决奇异性的问题，可以利用Newmann级数展开的方法，将[I-R]-1展开以避开奇异点：

[I-R]-1=I+R+R2+R3+R4+…RN+…

(8)

将式(8)代入式(6)，得到：

d=[I+R+R2+R3+R4+…RN+…]s

(9)

a=PU[I+R+R2+R3+R4+…RN-1+…]s

(10)

其中，RNs表示波经过了N次节点回传。

结合式(9)和式(10)可知，经过N次节点回传后传至接收点的波，入射波较出射波多传播一次。究其原因，是由于局部坐标系采用了对偶坐标系。

波在经过节点时既有反射，又有透射。以首次到达32单元节点3的入射波作为结构节点3的入射波，入射波到达节点3经过一次回传后沿32单元传播的出射波作为节点3的反射波，沿34、35单元传播的出射波作为结构节点3的透射波。入射波、反射波与透射波的表达式如下所示：

νi=iωa132(0)ei*k1*0

νr=iωd132(1)e-i*k1*0

νt34=iωd134(1)e-i*k1*0

νt35=

2结构的瞬态波动响应分析

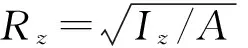
2.1节点位移协调及力平衡关系

由基本原理可知，回传射线矩阵是基于受力平衡及位移协调条件建立的，结构上任意点处均满足此两条件。

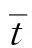
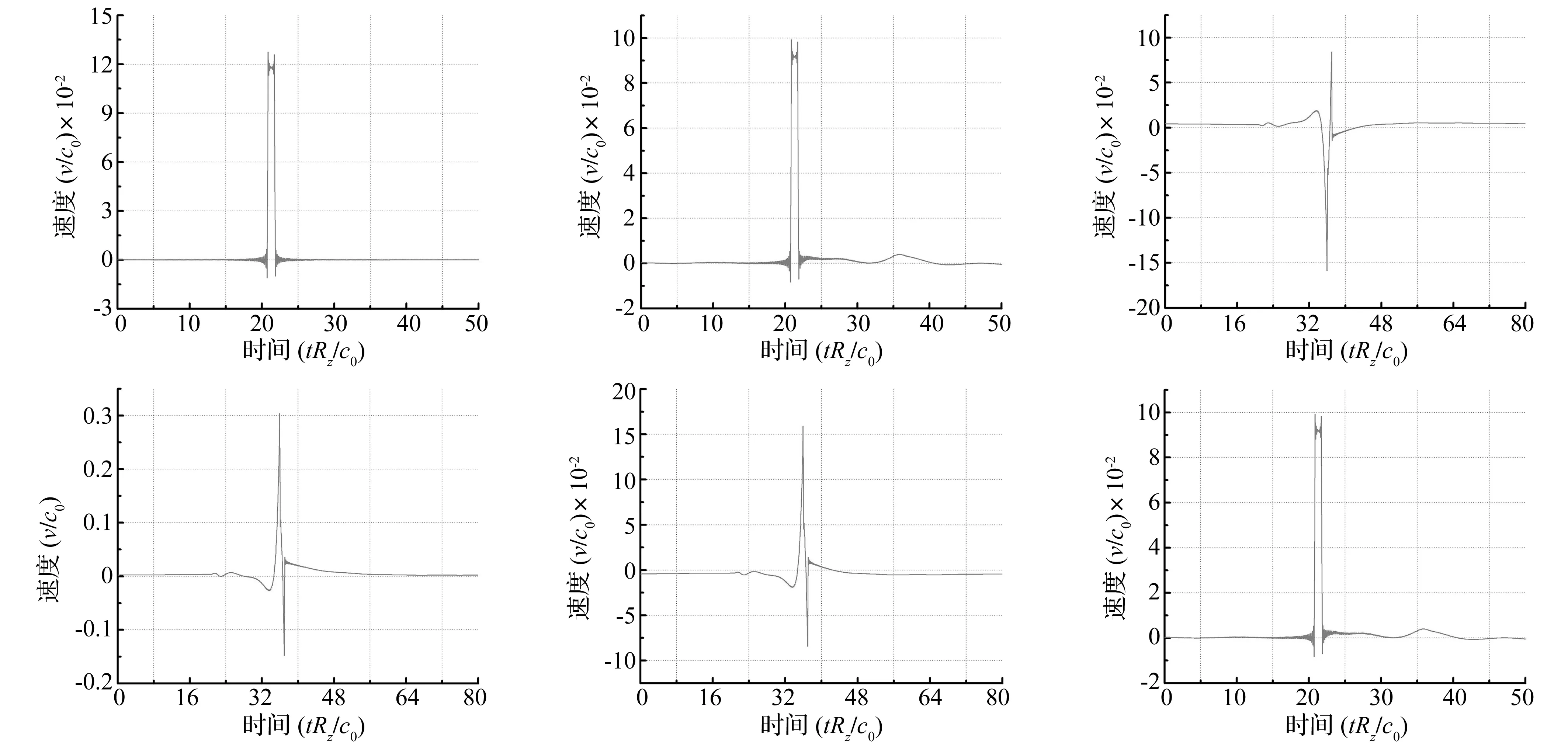
(a) 节点3在23单元节点2处局部坐标系下的纵向及横向速度波(b) 节点3在34单元节点3处局部坐标系下的纵向及横向速度波(c) 节点3在35单元节点3处局部坐标系下的纵向及横向速度波图3 相交于节点3的各单元3点处的纵向及横向速度波Fig.3Longitudinalandtransversewavesatjoint3ofeachelementthatintersectedatjoint3

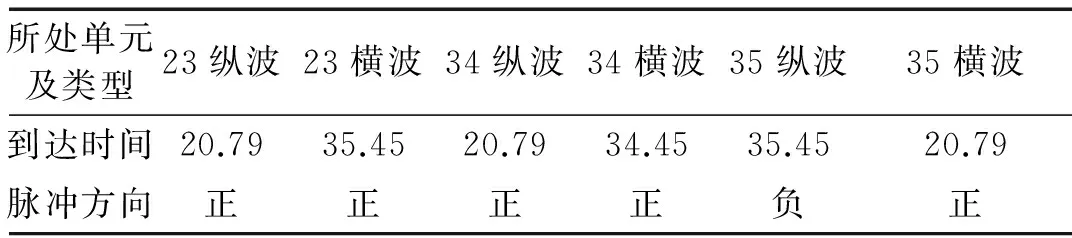
表1　相交于节点3的各单元3点处的综向及横向速度波特征

节点2处有作用力，因此与结构节点2相连的各单元的节点2处的轴力及剪力之和等于f(t)在水平和竖直方向分力的无量纲值。节点3无外力作用，与结构节点3相连的各单元的节点3处的合力为零。节点2、3处的受力示意图及受力平衡如图4～6所示。

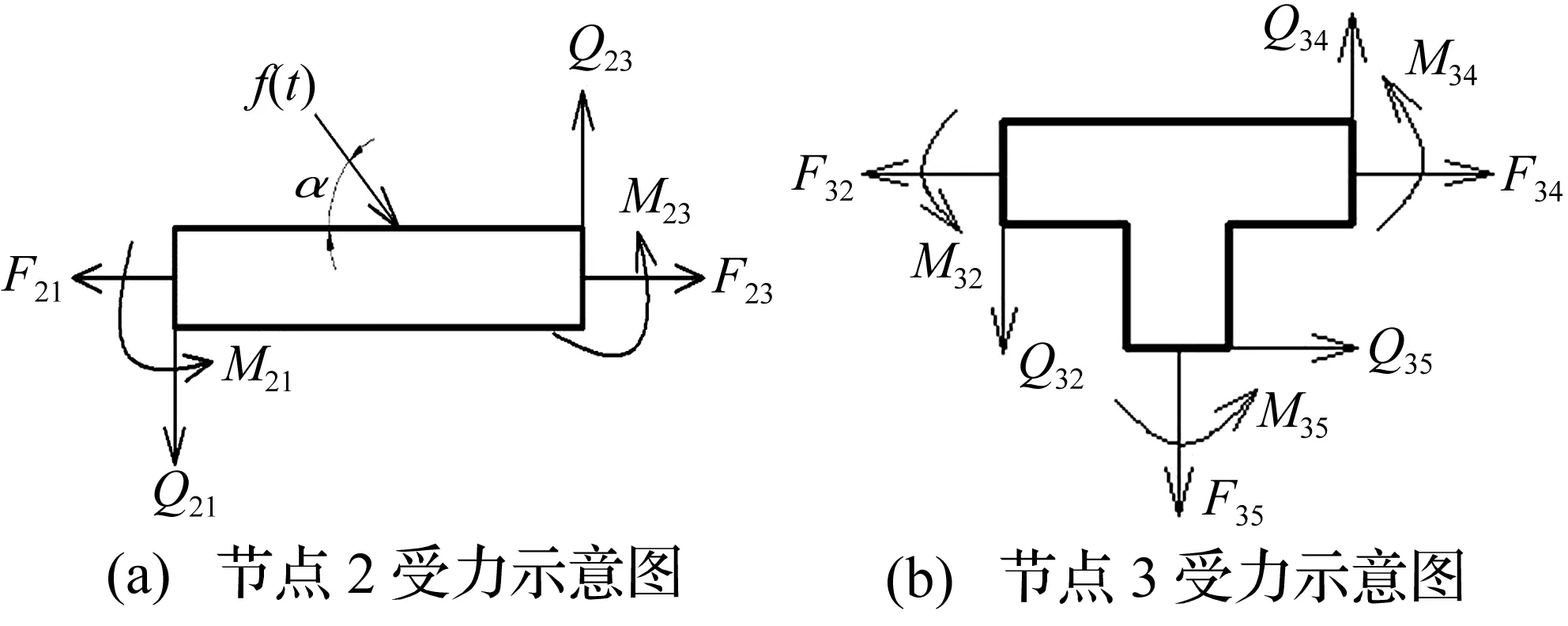
图4　节点2、3的受力示意图Fig.4 The forcediagram of joint 2 and 3

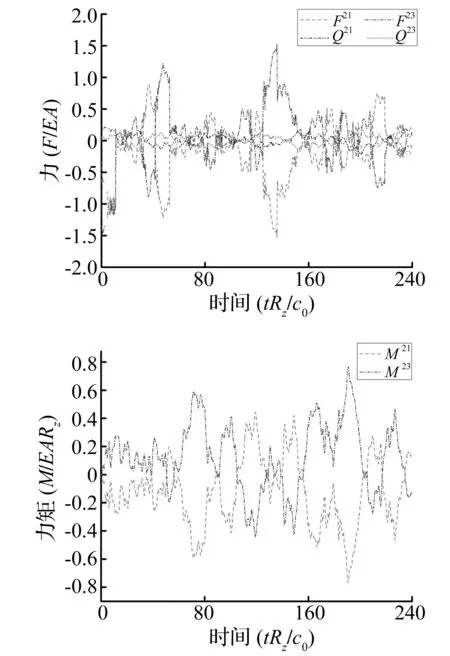
图5　整体坐标系下节点2的轴力、剪力及弯矩Fig.5 Axial, shear force and moment at joint 2 in global coordinate

图6　整体坐标系下节点3的水平向力及弯矩Fig.6 Horizontal force and moment at joint 2 in global coordinate

2.2速度波的传播

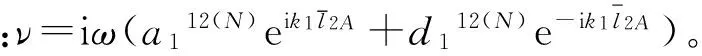
在方波脉冲激振力作用下经过N次节点回传后到达接收点的纵向速度波的传播路径、波的传播类型及传播时间如表2所示。

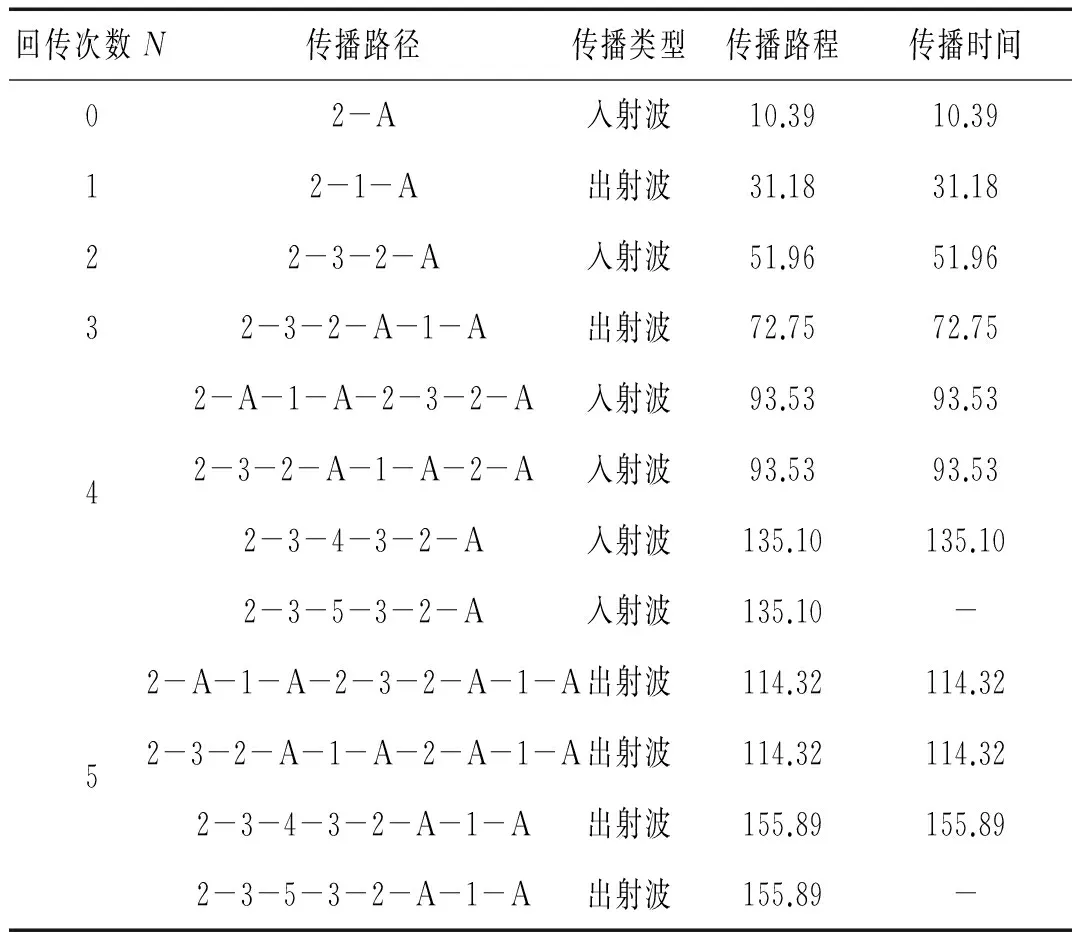
表2　经过N次节点回传后到达接收点的纵向速度波的传播路径、类型及时间

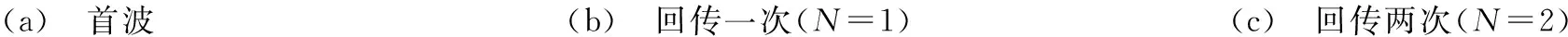
(a) 首波(b) 回传一次(N=1)(c) 回传两次(N=2)

(d) 回传三次(N=3)(e) 回传四次(N=4)

(f) 回传五次(N=5)(g) 经过接收点的前五条波图7 到达接收点A的纵向速度波Fig.7LongitudinalvelocitywavereachedthereceiverA

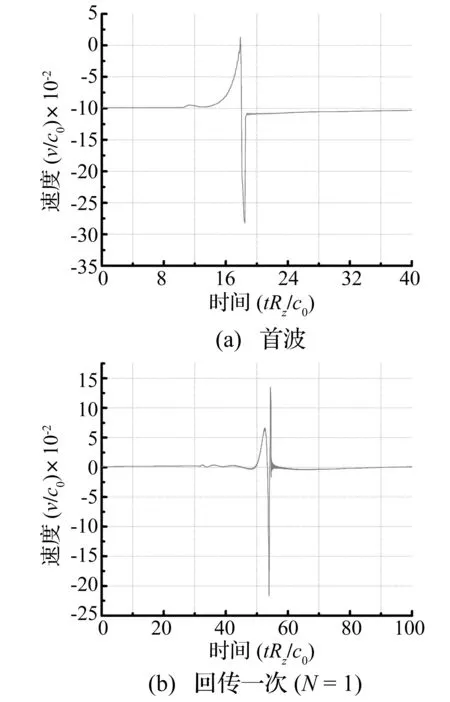
图8　到达接收点处的首波及经一次节点回传后到达接收点的横向速度波Fig.8 First and after areverberated horizontal velocity wave reached the receiver A

2.3节点处的反射波与透射波

波在经过节点时既有反射，又有透射。节点3处的首条入射波、反射波及透射波波形曲线如图9。由图9可知，反射波和透射波的脉冲方向均与入射波脉冲方向相反，透射波波形曲线和反射波波形曲线之和与入射波波形曲线等值反向，叠加之和为零。经过节点的两条透射波的波形曲线完全相同。

2.4结构的自振频率

利用回传射线矩阵法求得的结构自振频率与有限元软件ANSYS和SAP2000求得的结果对比见表3。

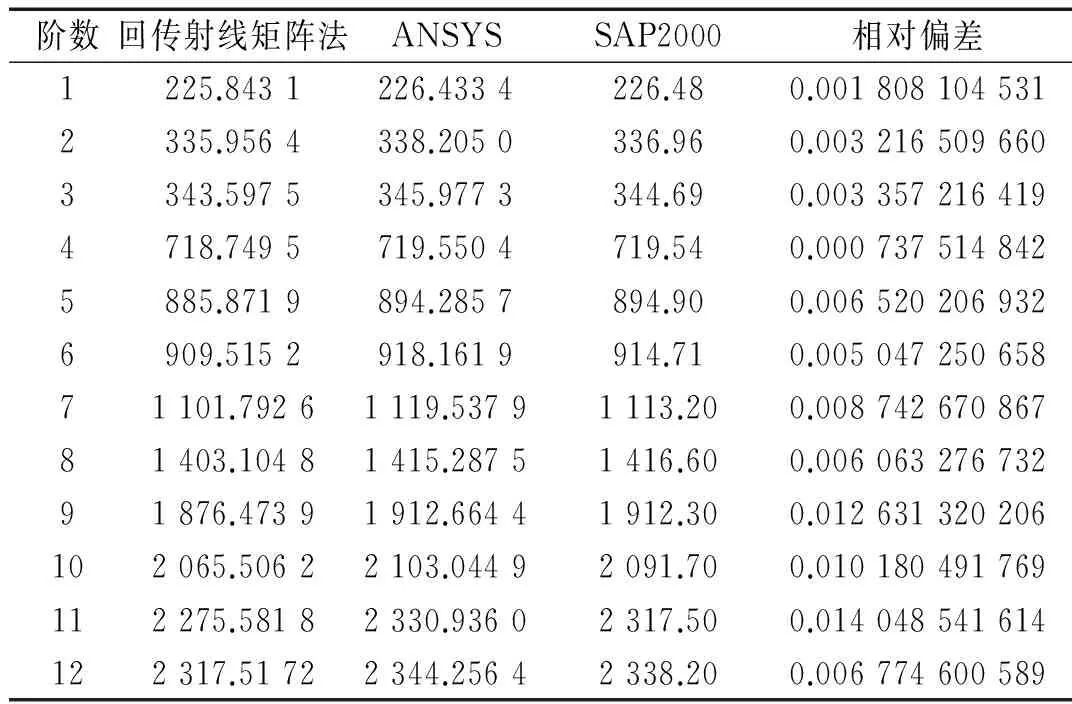
表3　T形框架前12阶自振频率

从表3的计算结果可以看出，利用回传射线矩阵法求得的自振频率同ANSYS和SAP2000求得的自振频率结果非常接近。证明利用回传射线矩阵法求解结构自振频率的方法是有效的。结构的自振特性只与结构的自身特性有关，而与外界因素如外荷载、时间等因素无关。因此，不同于结构的瞬态响应，利用该方法求解结构自振特性时，整个过程都是在频域中进行，而与时域无关。而结构的瞬态响应是时间的函数，因此其结果需通过傅里叶逆变换将其转换至时域中。回传射线矩阵法属于波动的方法，由于不考虑结构单元划分数目等因素，用该方法求得的结果具有高精度的优点。且易于编制通用程序进行计算。

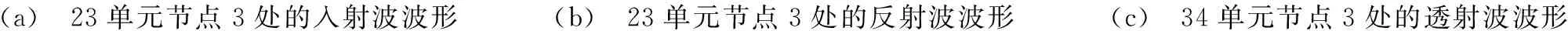
(a) 23单元节点3处的入射波波形(b) 23单元节点3处的反射波波形(c) 34单元节点3处的透射波波形

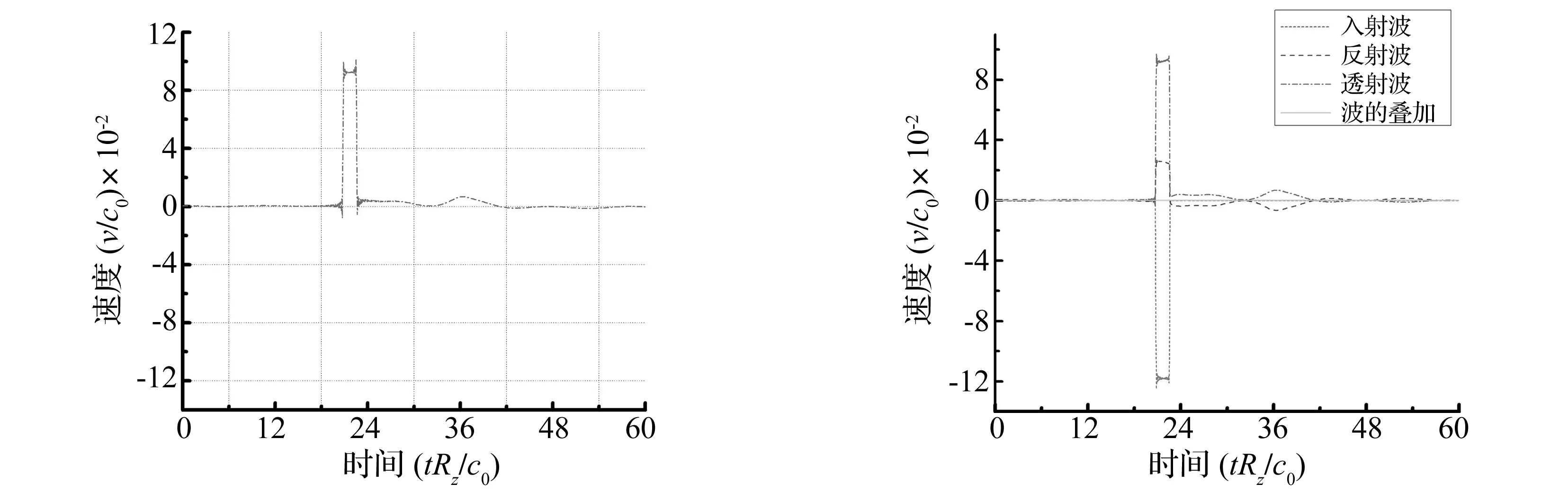
(d) 35单元节点3处的透射波波形(e) 入射波、反射波及透射波波形曲线叠加图9 节点3的入射波、反射波及透射波波形曲线及三条曲线的叠加Fig.9Thecurveofincident,reflectedandtransmitwaveandsuperpositionofthreecurvesatjoint3

3结论

本文基于回传射线矩阵法研究了T形框架在方波脉冲荷载作用下的波形特征，进一步求得该结构的自振频率，并与ANSYS和SAP2000计算结果进行对比。经过分析得到如下结论：

(2) 波在传播过程中经过节点时，会发生波的反射和透射。入射波在单元交界处会产生反射波和透射波，反射波脉冲方向与透射波脉冲方向均与入射波脉冲方向相反，反射波波形曲线和透射波波形曲线叠加之和与入射波波形曲线等值反向，三者叠加为零。

(3) 利用回传射线矩阵法可求解结构的任一阶自振频率。由于该方法属于波动的方法，不用考虑有限元方法的单元划分等因素的影响，求得的结果是精确解。

参 考 文 献

[1] Howard S M，Pao Y H.Analysis and experiments on stress waves in planar trusses[J]．Journal of Engineering Mechanics，1998，124(8)：884-891.

[2] Pao Y H.Chen W Q. Elastodynamic theory of framed structures and reverberation-ray matrix analysis[J]. Acta Mechanica,2009,204(1):61-79.

[3] 余云燕，鲍亦兴，陈云敏．有损伤框架结构中波动分析[J]．振动工程学报，2004，17(1)：20-24.

YU Yun-yan, PAO Yi-xing, CHEN Yun-min. Wave analysis of damaged frame structures[J]. Journal of Vibration Engineering，2004，17(1)：20-24.

[4] 余云燕．多缺陷框架结构的波动响应[J]．振动工程学报，2008，21(5)：511-515.

YU Yun-yan. Dynamic response of multi-defective frame structure[J]. Journal of Vibration Engineering，2008，21(5)：511-515.

[5] 余云燕．回传射线矩阵法分析埋置框架的瞬态动力响应[D]．杭州：浙江大学，2004.

[6] 余云燕，鲍亦兴，陈云敏．埋置框架质量检测的探讨[J]．力学学报，2006，38(3)：339-346.

YU Yun-yan, BAO Yi-xing, CHEN Yun-min.Disscussion on quality testing of frame structure embedded partially in soil[J]. Chinese Journal of Theoretical and Applied Mechanics，2006，38(3)：339-346.

[7] 余云燕．有缺陷埋置框架的波动响应及影响因素研究[J]．振动工程学报，2007，20(2)：194-199.

YU Yun-yan. Studies on wave response of a defected framestructure embedded partially in soil and influence factors [J]. Journal of Vibration Engineering, 2007,20(2): 194-199.

[8] 田家勇，苏先樾．刚架结构的节点质量阻尼减振分析[J]．固体力学学报，2002，23(1): 47-53.

TIAN Jia-yong,SU Xian-yue. The vibration suppression of joint massdamping in frame structures [J]. Acta Mechnica Solida Sinica, 2002,23(1): 47-53.

[9] 严蔚,袁丽莉．基于回传射线矩阵法的含裂缝智能梁的动态特性[J]．振动与冲击，2010，29(6)：101-104.

YAN Wei，YUAN Li-li. Dynamic analysis of a smart cracked beam based on the reverberation matrix method[J]. Journal of Vibration and Shock，2010，29(6)：101-104.

[10] 黄锦雄,朱幸科,韩卫东. 基于Timoshenko梁理论的深水油气井套管柱地震响应分析[J]. 振动与冲击，2013，32(7): 159-164.

HUANG Jin-xiong,ZHU Xing-ke,HAN Wei-dong. Seismic response of casing string of an oil and gas well in deepwater based on Timoshenko beam theory[J]. Journal of Vibration and Shock，2013，32(7)：159-164.

[11] 郭永强．回传波射矩阵法的理论及其应用[D]．杭州：浙江大学，2008.

[12] 郭永强．复杂空间框架结构的自振特性分析[J]．振动工程学报，2008，21(3)：261-267.

GUO Yong-qiang. Dynamic property analysis of complex space structures[J]. Journal of Vibration Engineering，2008，21(3)：261-267.

[13] 缪馥星.框架振动和瞬态响应的回传波射矩阵法研究[D]．上海：上海交通大学，2009.

Analysis of the transient response and natural frequency of a frame by the reverberation-ray matrix method

CHEN Jin-hao1, YU Yun-yan2

(College of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)

Abstract:Based on the method of reverberation-ray matrix, the reverberation-ray matrix of a of frame was established in accordance with the force balance, the displacement compatibility conditions of joints and the relationship between displacements at two ends of each element. On this basis, the characteristics of elastic wave propagation in the frame were analysed. The basic waveform characteristics of the incident wave, reflected wave and transmitted wave were discussed. The natural vibration frequency of the frame was solved and compared with the result by the finite element method. It is shown that both results are very close, and the effectiveness of the method was verified.

Key words:method of reverberation-ray matrix; elastic wave;frame structure; natural frequency

基金项目：国家自然科学基金资助(51268031);甘肃省基础研究创新群体资助(145RJIA332);甘肃省自然科学基金资助(1107RJZA084)

收稿日期：2015-03-10修改稿收到日期：2015-06-08

通信作者余云燕 女，博士,教授,博士生导师，1968年生

中图分类号:TU323.5

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.10.013

第一作者 陈进浩 男，硕士生，1988年生