基于钢轨振动响应分析的车轮扁疤检测方法研究

史红梅， 赵　蓉， 余祖俊， 朱力强

(北京交通大学 机械与电子工程学院，北京　100044)

基于钢轨振动响应分析的车轮扁疤检测方法研究

史红梅， 赵蓉， 余祖俊， 朱力强

(北京交通大学 机械与电子工程学院，北京100044)

摘要：车轮扁疤会影响列车运行舒适性并加速车辆、轨道基础设施部件故障。提出一种基于钢轨振动响应的车轮扁疤动态检测和识别方法。通过建立车辆轨道垂向耦合模型和车轮扁疤模型，计算车轮扁疤作用下的钢轨动态响应。比较了不同轨道不平顺、不同列车运行速度以及不同扁疤深度条件下，对钢轨振动响应进行Hilbert-Huang变换(HHT)和高阶谱分析两种方法的车轮扁疤识别能力。利用HHT中的Hilbert谱可以定性区分正常车轮与有扁疤车轮，但该方法会受到轨道不平顺大小的影响。而利用高阶谱分析方法能够定量判断扁疤深度，且识别能力不受轨道不平顺大小及运行速度影响。研究结果表明，利用钢轨振动响应结合高阶谱分析可以有效检测和识别车轮扁疤。

关键词：钢轨振动响应；车轮扁疤；车辆轨道耦合模型；Hilbert谱；高阶谱

列车运行过程中常因空转打滑或制动抱死等原因造成车轮擦伤形成扁疤。带扁疤的车轮在运行时会在轮轨间产生周期性的冲击，引起车辆轨道耦合系统的振动加剧，影响乘坐舒适性，加速对车辆和轨道部件的破坏，严重时将危及行车安全。因此对车轮扁疤的实时检测十分必要。

目前国内外对车轮扁疤的检测方法已有很多。文献[1]通过图像处理法检测车轮踏面缺陷，对车轮缺陷识别率较高，但系统结构复杂，且只适用于低速；文献[2]利用电信号检测法进行车轮扁疤识别，能够获得车轮扁疤深度，但无缝钢轨线路不适合使用此方法；文献[3]利用超声波检测车轮踏面缺陷，对车轮缺陷识别效果很好，但此方法技术难度和造价明显较高，而且没有具体指标用于判断扁疤深度；文献[4-5]利用轴箱加速度和信号处理算法检测车轮扁疤，此方法虽然能够实现对车轮全过程的实时检测，但安装传感器数目太多，成本较高，数据处理量太大，且没有研究轨道不平顺大小对其识别能力的影响；文献[6]通过轨道振动加速度法检测车轮扁疤，该方法能适应列车高低速运行时，实现对车轮扁疤的判别，并且性能稳定，但仅是定性区分了正常车轮与擦伤车轮，不能定量判断出车轮扁疤深度。

本文通过建立车辆轨道垂向耦合模型和车轮扁疤模型，仿真计算在车轮扁疤作用下的钢轨振动响应，研究了基于钢轨振动信号对车轮扁疤进行识别的方法，通过分析比较HHT和高阶谱分析方法在不同轨道不平顺、不同运行速度以及不同扁疤深度下的识别能力，表明利用钢轨振动响应结合高阶谱分析在定性与定量识别车轮扁疤上的可行性。

1车辆轨道垂向耦合动力学模型

车辆-轨道耦合模型采用文献[7]中的客车-轨道垂向非线性模型，由车辆模型和轨道模型组成。在车辆模型中将车辆模拟成一个以速度v运行于轨道结构上的多刚体系统，由车体、前后转向架和轮对组成，考虑了车体和转向架的垂向振动、点头，轮对的垂向振动，共10个自由度。轨道模型采用钢轨-轨枕-道床-路基三层结构，其中钢轨采用弹性点支撑的无限长Eular梁，轨枕采用刚体单元，道床在纵向上离散成道床块单元。车辆系统与轨道系统的垂向耦合作用是通过轮轨垂向接触而实现的，具体表现为轮轨之间的垂向作用力，在本文中采用的是最经典有效的Hertz非线性弹性接触模型。

车轮扁疤模型采用位移输入法模型[8],具体如下：

(1)

将扁疤等效的轨道不平顺模型与轨道的线路实测不平顺zg0(x)进行叠加作为新的轨道不平顺输入，实现车轮扁疤的输入。即为：

z0(x,t)=zg0(x,t)+ζ(x,t)

(2)

2基于HHT的车轮扁疤识别

HHT是Huang等人提出的一种时频分析方法[9]，包括经验模式分解(EMD)与Hilbert变换两部分。其中EMD完全脱离了傅里叶分析的框架，对非平稳信号和非线性信号处理具有很好的效果，因此HHT对于分析冲击性的、非平稳的扁疤信号非常适用。

2.1HHT原理

对信号作HHT分析，其具体过程如下：

(1) 对信号作EMD分解，获得n个基本模式分量IMF及原始信号的残差，即

(3)

(2) 对基本模式分量进行Hilbert变换，得到

(4)

2.2基于Hilbert谱的车轮扁疤识别

2.2.1不同轨道不平顺下的Hilbert谱

利用已建模型，分别计算两种轨道不平顺下的正常车轮与扁疤深度为0.1 mm的车轮的钢轨振动信号，运行速度为160 km/h，轨道不平顺分别为中国三大干线谱和德国低干扰谱，前者在幅值上要明显大于后者。仿真车辆运行距离为100 m，仿真时间为2.25 s。

图1(a)为中国三大干线谱下的正常车轮的Hilbert谱；图1(b)为中国三大干线谱下扁疤深度0.1 mm的车轮的Hilbert谱；图2(a)为德国低干扰谱下的正常车轮的Hilbert谱；图2(b)为德国低干扰谱下扁疤深度0.1 mm的车轮的Hilbert谱。

由图1(a)、图2(a)可看出，在不同轨道不平顺下，正常车轮对应的钢轨振动信号的Hilbert谱均随时间呈均匀分布。同时由图2(b)可看出在德国低干扰谱下车轮扁疤深度为0.1 mm时对应的钢轨振动信号Hilbert谱在扁疤存在的时刻呈纵向条纹状分布。但图1(b)中三大干线谱下车轮扁疤深度为0.1 mm时对应的钢轨振动信号Hilbert谱能量向扁疤存在时刻集中趋势不明显，大体仍随时间呈均匀分布，所以利用Hilbert谱不能识别出中国三大干线谱下扁疤深度为0.1 mm的车轮。因此可得出：在扁疤深度较浅时，轨道不平顺的大小会影响Hilbert谱区分正常车轮与扁疤车轮；轨道不平顺越大，Hilbert谱的区分能力越弱。

(a) 正常车轮作用下(b) 扁疤深度0.1mm的车轮作用下(a) 正常车轮作用下(b) 扁疤深度0.1mm的车轮作用下图1 中国三大干线谱下的钢轨振动响应Hilbert谱Fig.1TheHilbertspectrumofrailvibrationresponseswithChinesethreemainlinesirregularity图2 德国低干扰谱下的钢轨振动响应Hilbert谱Fig.2TheHilbertspectrumofrailvibrationresponseswithGermanlowinterferenceirregularity

2.2.2不同扁疤深度车轮的Hilbert谱

分别计算了0.2 mm、0.4 mm、0.8 mm 三种不同车轮扁疤深度时钢轨振动信号，列车运行速度为160 km/h；轨道不平顺为中国三大干线谱。图3为不同扁疤深度下对应的钢轨振动信号的Hilbert谱。

由图3(a)～(c)可看出，当车轮存在扁疤时，其钢轨振动信号的Hilbert谱能量主要集中在扁疤存在的时刻，呈纵向条纹状分布。结合图1 (a)可知正常车轮与带扁疤车轮的Hilbert谱间存在明显差异，所以利用HHT的Hilbert谱能够有效区分正常车轮与有扁疤车轮。但从图3中可看出不同扁疤深度对应的Hilbert谱间形态差异并不显著，所以Hilbert谱只能用来定性区分正常车轮与擦伤车轮。

2.2.3不同车速下的Hilbert谱

分别对运行速度为80 km/h和120 km/h的钢轨振动信号进行了HHT分析。扁疤深度分别为0.2 mm、0.4 mm、0.8 mm，轨道不平顺为中国三大干线谱。

分析发现，运行速度为80 km/h、 120 km/h下的Hilbert谱与运行速度为160 km/h下的Hilbert谱类似，即运行速度对不同车轮状态下的Hilbert谱没有较大的影响。由此可知利用Hilbert谱能够区分不同运行速度下的正常车轮与扁疤车轮，即运行速度对Hilbert谱识别能力无影响。

由于篇幅限制，本文不再给出80 km/h和120 km/h速度下钢轨振动信号的Hilbert谱图。

(a) 扁疤深度为0.2mm(b) 扁疤深度为0.4mm(c) 扁疤深度为0.8mm图3 不同扁疤深度对应的钢轨振动信号的Hilbert谱(v=160km/h)Fig.3TheHilbertspectrumofrailvibrationresponsesindifferentflatdepths(v=160km/h)

3基于高阶谱的车轮扁疤识别

由于HHT谱对于不同轨道不平顺条件不具有适用性，因此本文研究了高阶谱分析方法处理钢轨振动信号，与传统的二阶统计量特征检测方法相比，高阶谱对抑制轨道不平顺这种非高斯有色噪声信号具有更优越的性能。

3.1高阶谱原理

高阶谱是一种处理非线性非高斯信号的有力工具，高阶累积量的多维傅里叶变换定义为高阶谱(或称多谱)。与功率谱相比，高阶谱可以抑制高斯噪声，分辨率高，并能够得到信号相位、能量和非线性等有用信息[10]。高阶谱中双谱的阶数最低，计算较为简单，但包含了高阶谱的所有特征，所以本文中采用了基于三阶谱也称双谱的特征提取方法。

双谱可以由信号的离散傅里叶变换表示为

Bx(f1,f2)=E[X(f1)X(f2)X*(f1+f2)]

(5)

式中：X(fi)为信号的离散傅里叶变换；fi为频率变量；i=1,2；E[]表示数学期望。

双谱为复值谱，有2个频率变量f1和f2，双谱在f1和f2构成的频率平面内共有12个对称区域，因此，无需计算所有频率点上的双谱值，只需要计算主区域内的双谱值，再根据其对称性即可以求出(f1,f2)平面上的所有双谱值．双谱估计有直接法和间接法2种：直接法先估计其傅里叶序列，然后对该序列作三重相关运算，即可得到双谱估计；间接法先估计三阶累积量，再取累积量序列的傅里叶变换得到双谱[11]。本文中双谱估计采用间接法。

3.2基于高阶谱的车轮扁疤特征提取

3.2.1不同轨道不平顺下的高阶谱分析

分别对中国三大干线谱和德国低干扰谱下的正常车轮和车轮扁疤深度为0.1 mm对应的钢轨振动信号进行了高阶谱分析。

图4为中国三大干线谱下的正常车轮与车轮扁疤深度为0.1 mm所对应的钢轨振动信号的二维等高线图、三维双谱图；图5为德国低干扰谱下的正常车轮与车轮扁疤深度为0.1 mm所对应的钢轨振动信号的二维等高线图、三维双谱图。

(a) 正常车轮作用下的二维等高线(b) 扁疤深度0.1mm车轮作用下的二维等高线图(c) 正常车轮作用下的三维双谱图(d) 扁疤深度0.1mm车轮作用下的三维双谱图图4 中国三大干线谱下的钢轨振动响应高阶谱估计Fig.4High-orderspectrumestimationofrailvibrationresponseswithChinesethreemainlinesirregularity

(a) 正常车轮作用下的二维等高线(b) 扁疤深度0.1mm车轮作用下的二维等高线图(c) 正常车轮作用下的三维双谱图(d) 扁疤深度0.1mm车轮作用下的三维双谱图图5 德国低干扰谱下的钢轨振动响应高阶谱估计Fig.5High-orderspectrumestimationofrailvibrationresponseswithGermanlowinterferenceirregularity

从图4、图5可知，在不同轨道不平顺下，正常车轮与有扁疤车轮的二维等高线图的区别明显，由三维双谱图可看出车轮有扁疤时对应的的幅值要远远高于车轮正常时对应的幅值；同时，车轮有扁疤时其频率向中心处聚拢，而车轮正常时频率在整个平面均有分布。因此，利用高阶谱能够区分不同轨道不平顺下的正常车轮与擦伤车轮，与上节的Hilbert谱相比，高阶谱对轨道不平顺有着更好的抑制作用，即轨道不平顺大小不影响利用高阶谱分析进行扁疤识别的能力。

3.2.2不同扁疤深度下的高阶谱分析

对0.2 mm、0.4 mm、0.8 mm三种不同扁疤深度作用下的钢轨振动信号进行高阶谱分析。运行速度为160 km/h，轨道不平顺功率谱为中国三大干线功率谱。

图6(a)～(f)为不同扁疤深度下对应的钢轨振动

(a) 扁疤深度为0.2mm的二维等高线图(b) 扁疤深度为0.2mm的三维双谱图(c) 扁疤深度为0.4mm的二维等高线图(d) 扁疤深度为0.4mm的三维双谱图

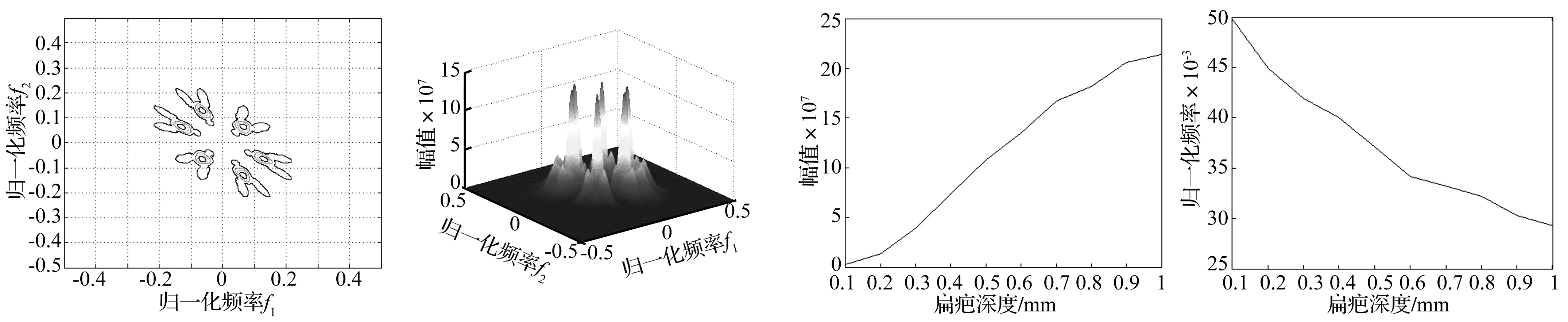
(e) 扁疤深度为0.8mm的二维等高线图(f) 扁疤深度为0.8mm的三维双谱图(g) 不同扁疤深度下的高阶谱峰值变化曲线(h) 不同扁疤深度下的高阶谱内扩频率变化曲线图6 不同扁疤深度的高阶谱估计(v=160km/h)Fig.6High-orderspectrumestimationofrailvibrationresponseswithdifferentwheelflatdepths(v=160km/h)

信号的二维等高线图、三维双谱图；图6(g)～(h) 为160 km/h速度下高阶谱频率、幅值随着扁疤深度的变化曲线，其中频率为二维等高线图的内扩对角频率，幅值为三维双谱图的对角切片的最大幅值。

由图6(a)～(f)可见，随着扁疤深度的增大，频率逐渐向内扩展，峰值也逐渐增大。不同的扁疤深度对应着不同的扩展频率与峰值。此信息也可由图6(g)～(h)更直观的反映出来。因此可以通过该信息实现对扁疤深度的定量判断。

3.2.3不同车速下的高阶谱分析

分别对运行速度为80 km/h和120 km/h的钢轨振动信号进行了高阶谱分析。扁疤深度取0.1 mm到1 mm，间隔为0.1 mm，轨道不平顺为中国三大干线谱。图7为120 km/h速度下高阶谱频率、幅值随着扁疤深度的变化曲线。其中频率为二维等高线图的内扩对角频率，幅值为三维双谱图的对角切片的最大幅值。

利用高阶谱分析方法，在运行速度分别为80 km/h和120 km/h下的有扁疤车轮对应的钢轨振动信号的二维等高线图和三维双谱图与运行速度为160 km/h下类似，均是不同的扁疤深度对应着不同的扩展频率与峰值，即运行速度不影响高阶谱分析方法对车轮扁疤的识别能力。由于篇幅限制，此处只给出高阶谱频率、幅值随着扁疤深度的变化曲线，不再给出高阶谱图。

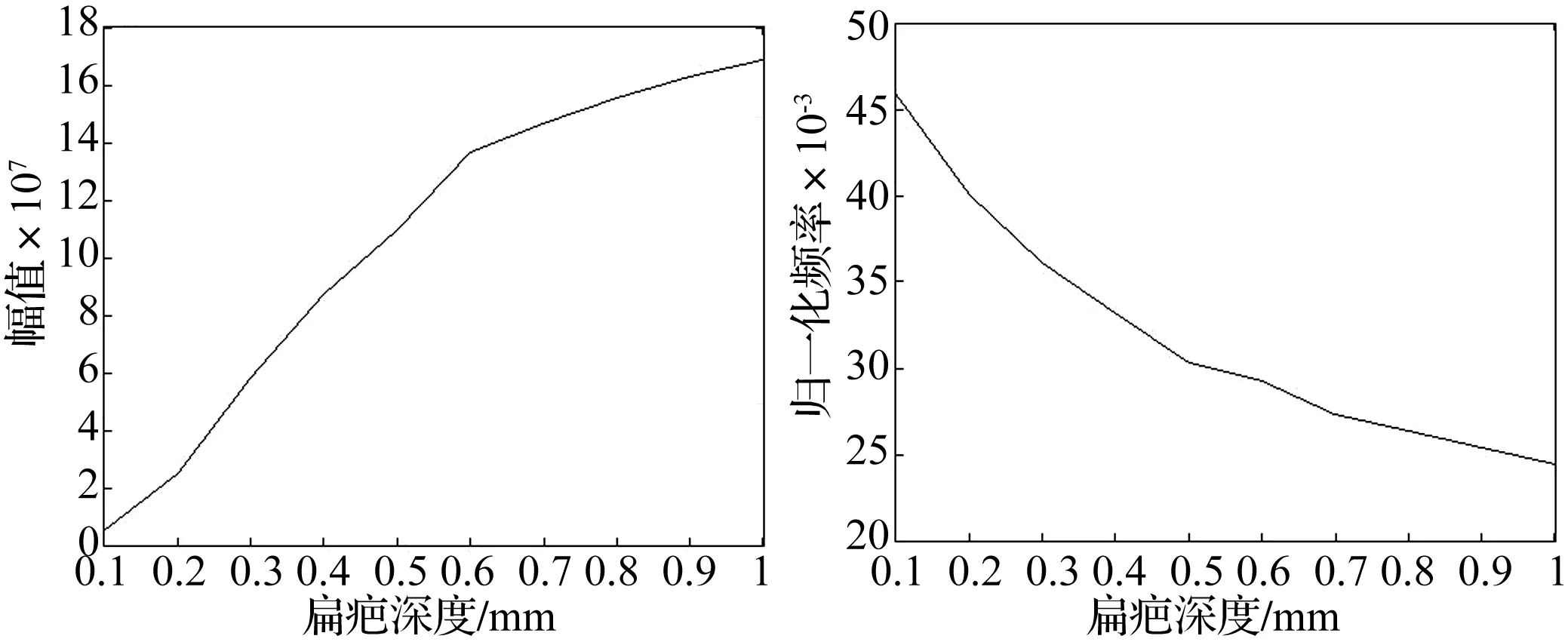
(a) 不同扁疤深度下的高阶谱峰值变化曲线(b) 不同扁疤深度下的高阶谱内扩频率变化曲线图7 高阶谱频率、峰值随着扁疤深度的变化曲线(v=120km/h)Fig.7Thefrequencyandpeakvalueofhigh-orderspectrumalongwiththevariationoftheflatdepth(v=120km/h)

4结论

本文通过建立车辆轨道耦合动力学模型和车轮扁疤模型，仿真计算了正常车轮和扁疤车轮作用下的钢轨振动信号，通过采用HHT和高阶谱对钢轨振动信号进行分析，得到结论如下：

(1) 有扁疤车轮的Hilbert谱呈纵向条纹分布，正常车轮的Hilbert谱呈均匀分布，且运行速度大小并不影响Hilbert谱对车轮扁疤的识别能力，但轨道不平顺大小会影响识别。另外不同扁疤深度的Hilbert谱形态区别不大，因此Hilbert谱法只能定性区分正常车轮与有扁疤车轮。

(2) 通过对不同轨道不平顺、不同车速、不同扁疤深度下的钢轨振动信号进行高阶谱分析可知轨道不平顺大小及车速大小并不影响高阶谱分析方法对车轮扁疤的识别能力，同时钢轨振动响应的高阶谱中不同扁疤深度对应的峰值、扩展频率信息也不同，可以利用此信息对车轮扁疤进行定量判断，实现基于钢轨振动信号的车轮扁疤的检测。

参 考 文 献

[1] 田丽丽，方宗德，赵勇. 铁路货车车轮踏面伤损检测中剥离与擦伤定位方法[J]. 铁道学报，2009，31(5)：31-36.

TIAN Li-li, FANG Zong-de, ZHAO Yong. Locating methods of peeling and flat spots in detection of wheel tread damages of railway wagons [J]. Journal of the China Railway Society, 2009，31(5)：31-36.

[2] 王方程，迟宝全. 平轮在线自动检测方法综述[J]. 城市轨道交通研究，2006，9(1)：31-33.

WANG Fang-cheng, CHI Bao-qian. On the on-line automatic detection method of flat wheel [J]. Urban Mass Transit, 2006，9(1)：31-33.

[3] 戴立新，韩激扬，王泽勇，等. 车轮电磁超声探伤技术及自适应滤波算法研究[J]. 铁道学报， 2010，32(4)：114-118.

DAI Li-xin, HAN Ji-yang, WANG Ze-yong, et al. Research on EMAT used in wheel flaw detecting and adaptive filtering algorithm [J].Journal of the China Railway Society, 2010，32(4)：114-118.

[4] Liang B, lwnicki S D, Zhao Y,et al. Railway wheel-flat and rail surface defect modeling and analysis by time-frequency techniques [J].International Journal of Vehicle Mechanics and Mobility,2013,51(9):1403-1421.

[5] 李奕璠，林建辉，刘建新，等. 车轮踏面擦伤识别方法[J]. 振动与冲击，2013，32(22)：21-27.

LI Yi-fan, LIN Jian-hui, LIU Jian-xin, et al. Identification method of wheel tread flat [J]. Journal of Vibration and Shock, 2013, 32(22): 21-27.

[6] 马莉，任健，王泽勇，等. 基于DSP的车轮踏面擦伤检测系统[J]. 现代电子技术，2009(17)：149-152.

MA Li, REN Jian, WANG Ze-yong, et al. Wheel tread scratch detection system based on DSP [J]. Modern Electronics Technique, 2009(17): 149-152.

[7] 翟婉明. 车辆-轨道耦合动力学[M]. 北京：科学出版社，2007：12-19.

[8] Ding Jian-ming, Lin Jian-hui, Wang Guang-ming, et al. Time-frequency analysis of wheel-rail shock in the presence of wheel flat [J]. Journal of Traffic and Transportation Engineering, 2014, 1(6): 457-466.

[9] 李忠继，魏来，戴焕云，等. 基于Hilbert-Huang变换的车轮扁疤识别方法[J]. 交通运输工程学报，2012，12(4)：33-41.

LI Zhong-ji, WEI Lai, DAI Huan-yun, et al. Identification method of wheel flat based on Hilbert-Huang transform [J]. Journal of Traffic and Transportation Engineering, 2012，12(4)：33-41.

[10] 孙洁娣，靳世久. 基于小波包能量及高阶谱的特征提取方法[J]. 天津大学学报，2010，43(6)：562-566.

SUN Jie-di, JIN Shi-jiu. Feature extraction method based on wavelet packet energy and high-order spectrum [J]. Journal of Tianjin University, 2010，43(6)：562-566.

[11] 李玉韩，蔡坤宝，张继红. 双谱估计在中医脉象信号分析中的应用[J]. 重庆大学学报：自然科学版，2006，29(5)：44-47.

LI Yu-han, CAI Kun-bao, ZHANG Ji-hong. Application of bispectrum estimation to analyzing pulse signals [J]. Journal of Chongqing University: Natural Science Edition,2006,29(5):44-47.

Detection method for wheel flats based on rail vibration responses analysis

SHI Hong-mei, ZHAO Rong, YU Zu-jun, ZHU Li-qiang

(School of Mechanical, Electrical Control Engineering, Beijing Jiaotong University, Beijing 100044, China)

Abstract:Wheel flats will influence ride comfort and result in rapid deterioration of vehicle and infrastructure components. A dynamic detection and identification method for wheel flat was proposed based on the rail vibration responses analysis. A vehicle-track vertical coupling system and its wheel flat were modelled and the rail dynamic responses were calculated in the condition of wheel flat. Two methods, Hilbert-Huang transformation (HHT) and higher-order spectrum, used to analyze the rail vibration responses and identify the wheel flat were presented and compared. The influences of different track irregularity, train speed and wheel flat depth on the identification ability of the methods were analyzed. The Hilbert spectrum can qualitatively distinguish the normal wheel and the wheel with flats, but the detection ability is affected by the track irregularity. The high-order spectrum can express the different wheel flat depth quantitatively and it isn’t influenced by the track irregularity and train running speed. The investigation shows the rail vibration responses combined with high-order spectrum analysis can detect wheel flats effectively.

Key words:rail vibration responses; wheel flat; vehicle-track coupling model; Hilbert spectrum; high-order spectrum

基金项目：国家自然科学基金重点项目(61134003)

收稿日期：2015-08-03修改稿收到日期：2015-10-05

中图分类号:U270.7

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.10.004

第一作者 史红梅 女,博士，副教授，1973年8月生