基于有限测点的高拱坝原型整体动位移场反演研究

李火坤, 邓冰梅, 魏博文, 黄锦林, 符　晓

(1.南昌大学 建筑工程学院,南昌　330031;2.天津大学 水利工程仿真与安全国家重点实验室,天津　300072;3.广东省水利水电科学研究院,广州　510635;4.华东勘测设计研究院有限公司,杭州　310014)

基于有限测点的高拱坝原型整体动位移场反演研究

李火坤1,2, 邓冰梅1, 魏博文1, 黄锦林3, 符晓4

(1.南昌大学 建筑工程学院,南昌330031;2.天津大学 水利工程仿真与安全国家重点实验室,天津300072;3.广东省水利水电科学研究院,广州510635;4.华东勘测设计研究院有限公司,杭州310014)

摘要：坝身泄洪的拱坝振动位移均方差是反映坝体振动强烈程度的重要指标，由于开展拱坝原型振动测试的测点有限，难以全面准确反映拱坝坝体的整体振动响应场分布特性，仅利用有限测点的动位移均方差进行坝体振动安全评价显得不够全面和具体，因此通过有限测点的实测响应反演出整个坝体结构的动位移场具有重要意义。以二滩高拱坝为工程实例，对其开展了原型泄洪振动测试，通过布置于坝体上的有限测点的原型实测动位移响应，基于遗传算法和有限元模态分析对该拱坝原型整体动位移场进行了反演，并给出了拱坝原型动位移场反演的具体流程图；反演结果表明，仅利用坝体顶拱拱圈的7个动位移响应测点实测值反演出了整个拱坝在泄洪工况下的动位移场，且反演结果与实测结果较为吻合，该方法为高拱坝的泄洪振动安全的正确评估提供了新的技术手段。

关键词：高拱坝；有限测点；原型振动测试；动位移响应；反演方法

水流诱发溢流高拱坝的振动在水利工程中较为常见，坝体的强烈振动会影响枢纽安全运行甚至结构破坏，随着中国一批300 m级高拱坝的建设，高速泄洪水流诱发大坝的振动受到工程界的高度关注。高速泄洪水流诱发高拱坝的动力响应主要取决于作用于坝体的水流脉动荷载的整体效应，高拱坝泄洪水流脉动荷载是复杂的和多样的，主要包括坝体挑流水舌对水垫塘底板冲击产生的脉动荷载、水垫塘内水体对拱坝下游面的“涌浪”脉动荷载、作用于坝体泄洪孔口上的脉动荷载等三类[1]，研究表明，脉动荷载频谱表现为具有一定低频带宽的噪声谱性质[2]，荷载能量多集中在低频范围内，且泄流诱发拱坝振动响应的工作频率与拱坝的坝高相关，国内外高拱坝原型动力试验表明[3]，其低阶振动频率多在1.4～5 Hz之间，拱坝的坝高越高，其固有频率就越低，而且模态较为密集(密频)，从工程结构振动特征来看，结构振动频率越低，相应的振幅越大。研究表明，高拱坝泄洪振动位移响应时程可视为各态历经的平稳随机过程，符合正态分布，基于泄流振动响应对坝体运行安全评价主要是从时域(幅值域)和频域角度分析坝体的泄洪振动状态，其中时域分析主要提取坝体振动位移均方差σ和最大位移振幅进行评估，动位移均方差反映的是坝体在平衡位置上的波动程度，坝体最大位移振幅反映的是坝体振动离开平衡位置的最大位移；对于动位移传感器所测的有限个测试样本数据而言，坝体最大位移振幅的估计一般取3倍的均方差σ(也即最大振幅位于[-3σ,+3σ]区间的概率为99.7%)进行统计。因此，坝体振动位移均方差σ集中体现了坝体的振动剧烈程度，是反映坝体振动强烈程度的重要指标。对于原型拱坝而言，开展原型振动测试的测点是有限的，因此利用有限测点的动位移反演出整个坝体的动位移场具有重要工程实践意义。

在结构振动反分析方面，苑希民等[4-6]提出了水工结构流激振动反分析方法，以水弹性模型为基础，对该方法进行了验证，并对水弹性模型中的不相似因素进行了修正；王富强等[7-8]基于模态叠加法对弧形闸门和拱坝的动应力进行了反分析，并与水弹性模型进行了对比验证；张建伟等[9]提出了基于小波正交算子变换的多振源反分析方法，并以高拱坝水弹性模型为例，通过有限测点的动位移响应反分析了作用于坝体的等效荷载时程线；王海军等[10]以某水电站厂房振动观测数据为依据，基于改进遗传算法对水轮机的动荷载进行了反演；李守巨等[11]以水轮机的振动响应数据为基础，采用径向基函数的人工神经网络，提出了水轮机振源荷载的识别方法；常晓通等[12]将待识别的动荷载以参数化形式进行表达，基于遗传算法对此类参数进行优化，通过使振动响应计算值与实测响应值误差最小，使参数化后的动荷载逐渐逼近真实荷载进行反演；本文以二滩高拱坝为工程实例，基于其有限测点的原型实测动位移响应，采用遗传算法对高拱坝原型整体动位移场进行了反分析，以反演出的等效荷载谱作为激励输入进行流激振动正分析求出坝体的整体动位移场，可为高拱坝原型泄洪振动安全的正确评估提供重要参考。

1高拱坝泄洪振动的动位移场反演方法

1.1脉动荷载作用下拱坝振动响应正分析基本原理

拱坝振动响应场的反演是以坝体泄洪振动响应正分析为基础的，计算高拱坝在脉动荷载作用下坝体结构振动响应时，本文是在以下三点假定条件下完成的：① 作用于坝体、坝基上的水流脉动荷载是一个各态历经的平稳随机过程；② 拱坝和地基为线弹性体；③ 拱坝坝体结构和地基振动时，将水体的作用以附加质量形式考虑，水与坝体的动力耦联相互作用是线性的，属于线性随机振动。

将拱坝离散为具有有限多个自由度的模型，其运动微分方程为[6]：

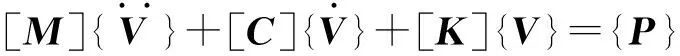
(1)

采用振型叠加法对式(1)进行求解，定义：

{V}=[φ]{δ}

(2)

式中，[φ]为模态矩阵；{δ}为振型广义的位移向量。

工程实践表明，高拱坝的泄洪振动主要是以低阶振动为主，若取拱坝振动的前q个振型，式(1)则分解成q个单自由度系统且相互独立的振动方程，其表达式如下：

(j=1,2,…,q)

(3)

式中，Mj、Kj、Cj分别为广义坐标下的质量、刚度和阻尼。Fj(t)为拱坝第j阶振型相对应的荷载分量，相应的表达式为：

(4)

式中，φij为i节点的第j阶振型模态向量，Pi(t)为作用于i节点的随机荷载分量，n为结构节点个数。

将式(3)两边同除以Mj，则有：

(5)

式中，ωj为拱坝第j阶圆频率，ζj为拱坝第j阶阻尼比。

由式(3)进一步求得拱坝第j阶的振型瞬态响应解为：

(6)

hj(t)为单位脉冲响应函数，可写为：

(7)

则拱坝任意节点k的振动位移响应时程可写为：

(8)

对拱坝任意节点k的振动位移响应的自相关函数进行FFT变换，并考虑拱坝结构各阶次振型的相互独立性，可得到节点k的动位移响应谱密度为：

(9)

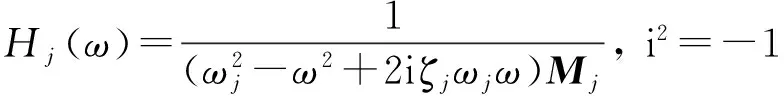
则k点动位移响应的均方差值为：

(10)

以上为高拱坝泄洪振动响应计算的正分析方法过程，在已知激励源随机荷载作用时，可求得结构整体动位移响应。对于高拱坝而言，泄洪时产生的随机水动力荷载难以测量，本文通过坝体有限测点动位移响应进行高拱坝脉动荷载振源反分析，首先计算作用于坝体上的等效荷载，然后基于反演得到的等效荷载谱进行上述过程的正分析计算，最后得到坝体结构的整体动位移响应场。

1.2高拱坝泄洪振动的动位移场反演

假设拱坝有K个动位移测点的实测值，需要反演N个等效荷载，对式(9)进行展开，可写为：

SVk(ω),k=1,2,…,K

(11)

将式(11)用矩阵方程可写成如下：

A{x}=B

(12)

(13)

(14)

(15)

对于溢流拱坝而言，其激励源荷载等效如下[1]：坝体挑流水舌对水垫塘底板冲击产生的脉动荷载P1、水垫塘内水体对拱坝下游面的“涌浪”脉动荷载P2以及作用于坝体泄洪孔口上的脉动荷载P3，如图1所示。坝体振动是这三种振动源共同作用的结果，其作用点和方向各不相同，本文将上述三个振源荷载视为三个独立、互不相关的荷载进行反演。

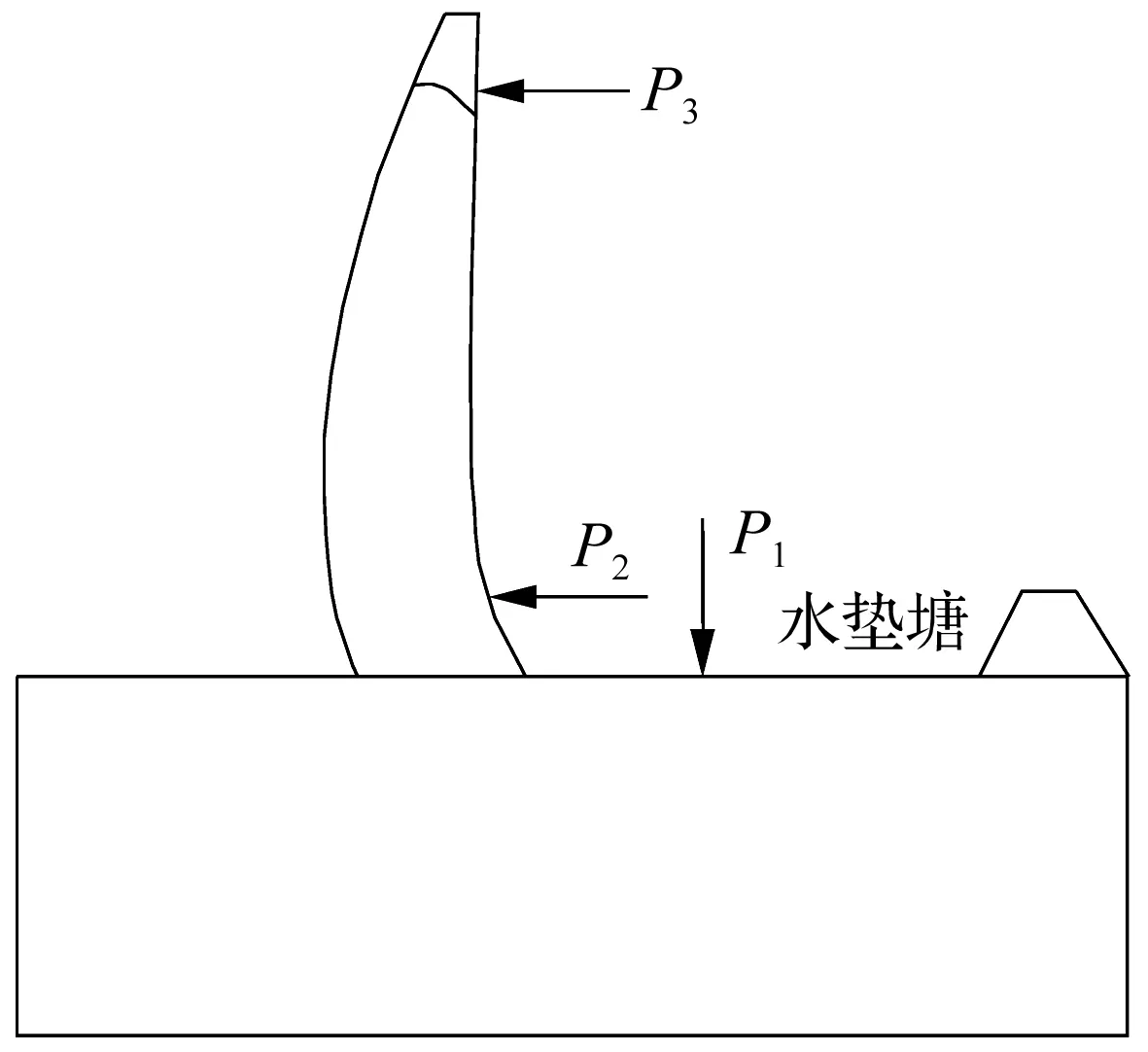
图1　拱坝等效激振源荷载示意图Fig.1 Vibration source schematic diagram on flow-induced vibration of arch dam

(16)

式中，θk是各实测点权重系数，本文取θk=1。

对于求最小值的条件∂S/∂SPii=0，可写成方程组的形式如下：

A′{x}=B′

(17)

对各圆频率ω进行遍历，可求得各等效荷载的功率谱，以此为输入进行相应的正分析，即可计算出整个拱坝坝体的动位移响应场。

2高拱坝原型泄洪振动的动位移响应场反演工程实例

2.1二滩拱坝原型泄洪振动测试

以二滩高拱坝为例，基于原型实测动位移响应对坝体整个结构动位移场进行反演分析。二滩拱坝为混凝土双曲拱坝，位于雅砻江上，如图2所示。拱坝顶部高程为1 205.00 m，最大坝高为240 m，坝顶拱圈弧长774.65 m，拱冠梁顶厚11 m，底厚55.74 m，弧高比3.23，跨高比2.83，厚高比0.232。在对拱坝进行原型泄洪振动测试时，对应的水位工况为：上游水位1 195.99 m，下游水位1 016.03 m，在坝顶2#～38#坝段，每间隔五个坝段布置1个径向动位移传感器，从左至右编号依次为B1～B7；在最大坝高的坝段(也即第二十个坝段)自顶部向下依次布置4个传感器，编号依次为B8～B11， 整个坝体动位移传感器布置如图3所示。动位移传感器型号为DP型地震低频振动位移传感器，频响范围0.35～150 Hz，灵敏度为15 mv/μm测试方向为径向(Y向)，如图4所示。信号采集和数据处理采用北京东方振动和噪声研究所研发的DASP测试分析系统，如图5所示，采样频率200 Hz。

图2　二滩拱坝Fig.2 Ertan arch dam

图3　二滩拱坝原型振动测试测点布置Fig.3 Sensors arrangement for ertan arch dam dynamic test

图4　DP型动位移传感器Fig.4 DP type dynamic displacement sensor

图5　DASP信号采集系统Fig.5 DASP signal acquisition system

B1-B11号动位移测点的动位移时程线及功率谱如图6～16所示，从各点动位移信号统计的均方差来看，坝体整体振动表现为由坝肩至坝顶中心越来越剧烈，振动均方差值越来越大，从功率谱图上看，靠近坝肩部位的测点振动信号频率成分较为丰富，如B2和B6测点，各包含有拱坝的4阶振动工作频率成分；但越靠近坝肩，相应的噪声干扰也越大，如B1和B7测点，坝体振动频率成分基本被噪声淹没，其功率谱表现为低频噪声谱性质。对于拱冠梁坝段测点，由于坝体高频分量的振动能量远小于低频分量的振动能量，以致在其功率谱图中所反映的坝体振动频率成分相对较少，高频信息被淹没，如B4、B8、B9、B10、B11测点仅含有1阶频率成分。拱坝坝体各测点的动位移均方差值统计及振动频率成分如表1所示。

表1　二滩拱坝各测点动位移均方差及频率成分

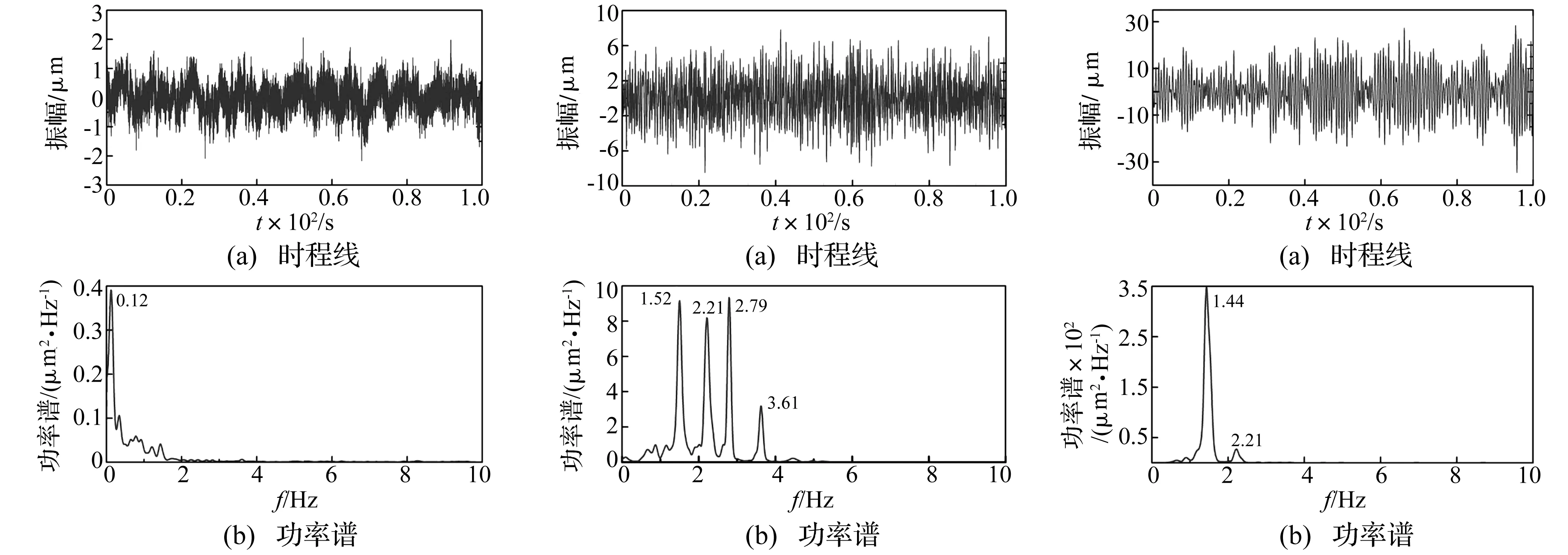
图6 B1测点动位移时程线及功率谱Fig.6TimehistorysignalsandpowerspectrumsofB1displacement图7 B2测点动位移时程线及功率谱Fig.7TimehistorysignalsandpowerspectrumsofB2displacement图8 B3测点动位移时程线及功率谱Fig.8TimehistorysignalsandpowerspectrumsofB3displacement

图9 B4测点动位移时程线及功率谱Fig.9TimehistorysignalsandpowerspectrumsofB4displacement图10 B5测点动位移时程线及功率谱Fig.10TimehistorysignalsandpowerspectrumsofB5displacement图11 B6测点动位移时程线及功率谱Fig.11TimehistorysignalsandpowerspectrumsofB6displacement

图12 B7测点动位移时程线及功率谱Fig.12TimehistorysignalsandpowerspectrumsofB7displacement图13 B8测点动位移时程线及功率谱Fig.13TimehistorysignalsandpowerspectrumsofB8displacement图14 B9测点动位移时程线及功率谱Fig.14TimehistorysignalsandpowerspectrumsofB9displacement

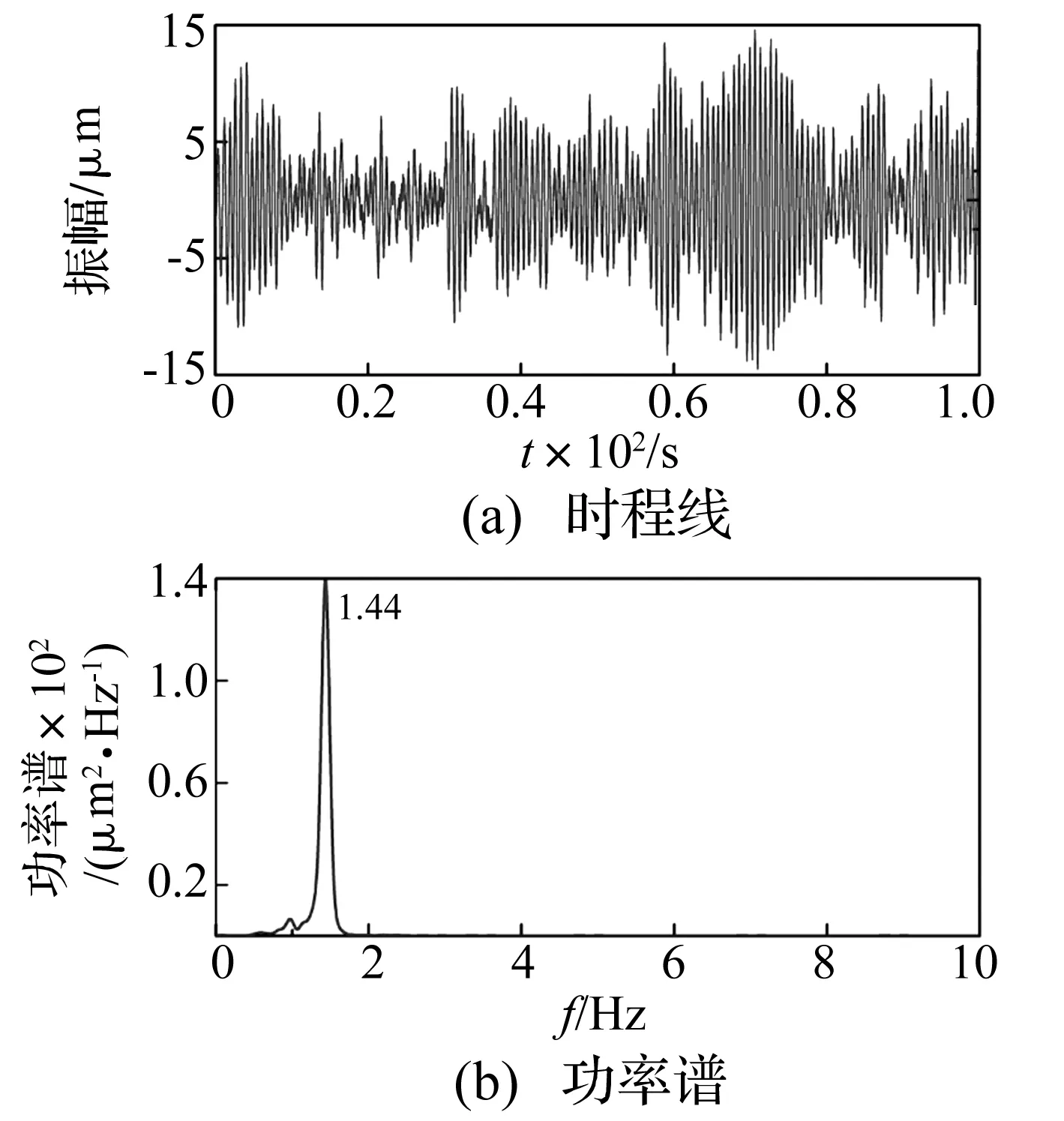
图15　B10测点动位移时程线及功率谱Fig.15 Time history signals and power spectrums of B10 displacement

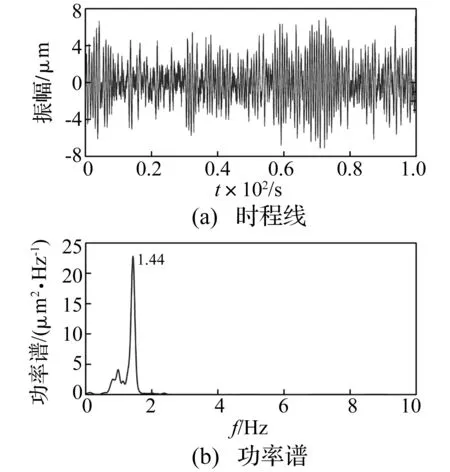
图16　B11测点动位移时程线及功率谱Fig.16 Time history signals and power spectrums of B11 displacement

2.2拱坝整体动位移场反演流程

2.2.1拱坝模态分析的有限元模型

从二滩拱坝实测点的功率谱图上看，拱坝的振动主要以低阶为主，在式(4)～式(9)的计算过程中，本文通过建立拱坝整体有限元模型进行模态分析，截取拱坝的前9阶模型作为计算模态提取振型φij、圆频率ωj及质量矩阵Mj。拱坝整体有限元模型参数及边界条件如下：坝体动态弹性模量E1=3.3×1010Pa，坝体材料密度ρ1=2 400 kg/m3，坝体泊松比μ1=0.167；基础动态弹性模量E2=3.0×1010Pa，基础材料密度ρ2=2 700 kg/m3，基础泊松比μ2=0.25；地基模拟范围为：深度取200 m，上游取124 m，下游边界取到水垫塘的末端，为534 m，左右坝肩取100 m；由于库水增加了坝体的惯性作用，水体的附加质量Mw采用修正的Westergaard公式进行计算，即：

(18)

式中，ρ0为水的密度，h0为水的深度，l为计算点到水面的距离。

拱坝整体有限元模型如图17所示，共划分有9 986个三维实体单元和12 218个节点，由于拱坝的泄洪振动以径向(Y方向)为主，因此本文进行坝体动位移场反演时提取Y方向节点动位移，提取部位为坝体有限元模型的下游面节点，共315个(分为十五层，每层21个节点)，节点编号如图18所示。

图17　拱坝有限元模型Fig.17 The finite element model of ertan arch dam

图18　坝体背面有限元网格及节点Fig.18 The finite element mesh and nodes on back of the dam

2.2.2基于遗传算法的方程式(16)最优求解

由于原型试验中存在水流等环境背景噪声的干扰，为使在求解方程式(16)时能快速的搜索到全局最优解，本文采用遗传算法对该方程进行最优求解，采用浮点编码，优化目标函数(适应度函数)为：

Fit(f(ω))=Cmax-f(ω)=

(19)

式中，Cmax为一足够大的数，且f(ω)

拱坝动位移场的反演流程如图19所示。

2.2.3反演结果

以B1～B7实测动位移功率谱及拱坝有限元模型模态计算所得前9阶振型、频率及质量矩阵作为输入(B8～B11实测点作为对反演结果的验证)，按图19所示流程进行反演，得到图18所示的坝体背面1～315号节点的动位移均方差值，坝体背面第一至十五层节点动位移分布如图20～22所示；以此数据为基础，采用TECPLOT软件绘制的坝体动位移场等值云图如图23所示，反演结果表明：拱坝坝体整体振动表现为随着高程的逐渐增加坝体振动均方差值越大，振动越剧烈，受两岸坝肩岩体的约束，在拱圈方向，动位移均方差值沿左右坝肩逐渐减小，且左右坝肩两侧动位移均方差呈基本对称分布；总体上，坝体顶部拱圈中部的振动最为强烈，坝体整体最大动位移均方差值出现在坝顶中部。

反演结果值与实测点(B1～B11)的数值对比如图24所示，反演结果与实测结果的总体变化趋势一致，拱坝坝体动位移响应均方差反演的最大值为14.08 μm，实测值为13.47 μm，误差为4.5%，验证了本文方法反演结果的准确性和可靠性。

图19　拱坝动位移场反演流程图Fig.19 The flowchart of the back analysis algorithm for arch dynamic displacement field

图20 坝体背面第一至第五层节点动位移均方差分布Fig.20Meansquareerrordistributiononthefirsttothefifthfloorofthedam图21 坝体背面第六至第十层节点动位移均方差分布Fig.21Meansquareerrordistributiononthesixthtothetenthfloorofthedam图22 坝体背面第十一至第十五层节点动位移均方差分布Fig.22Meansquareerrordistributionontheeleventhtothefifteenthfloorofthedam

图23 坝体动位移场反演结果等值云图Fig.23Equivalentcloudofdamdynamicdisplacementfieldinversionresults图24 计算值与实测值比较Fig.24Comparisonofthemeasuredresultsandcalculatedresults

3结论

通过结构有限测点动力响应反演整个结构动力响应场是工程振动控制领域的研究热点之一，在水工结构泄洪振动研究领域，结构振动位移响应均方差是反映坝体振动剧烈程度的重要指标之一，本文基于高拱坝泄洪振动响应特点及其激振源荷载特性，以二滩拱坝为工程实例，开展了拱坝原型泄洪振动测试，统计并分析了各实测动位移响应点均方差的分布特征，以原型有限实测动位移响应谱作为输入，基于遗传算法并结合拱坝有限元模型，对坝体结构的整体动位移场进行了反演，反演结果与实测点结果较为吻合，可为拱坝泄洪振动安全评价提供重要参考；此外，坝体动应力也是反映坝体结构振动安全的重要指标之一，以反演出的动位移场为基础，研究坝体动应力场的反演方法，本文将在后续研究中继续深入。

参 考 文 献

[1] 练继建，崔广涛，林继镛. 高拱坝泄洪振动的计算分析与验证[J]. 水利学报，1999,12:23-32.

LIAN Ji-jian, CUI Guang-tao, LIN Ji-yong. Analysis on flow-induced vibration of over flow high arch dam and its verification[J]. Journal of Hydraulic Engineering, 1999,12:23-32.

[2] 李火坤，练继建. 高拱坝泄流激励下基于频域法的工作模态参数识别 [J]. 振动与冲击，2008,27(7):149-153.

LI Huo-kun, LIAN Ji-jian. Operational modal parameter identification of high arch dam under flood discharge exciting based on frequency domain decomposition method[J].Journal of Vibration and Shock, 2008,27(7):149-153.

[3] 寇立夯，金峰，迟福东，等. 国内外混凝土拱坝原型振动试验分析[J]. 水力发电学报，2007, 26(5):31-37.

KOU Li-hang, JIN Feng, CHI Fu-dong, et al. Analysis of prototype dynamic test of concrete arch dams at home and abroad[J].Journal of Hydroelectric Engineering,2007,26(5):31-37.

[4] 苑希民，何玉敖，崔广涛. 结构动力的反分析方法研究[J]. 工程力学，1996(增刊1)：321-325.

YUAN Xi-min, HE Yu-ao, CUI Guang-tao.Study on structural dynamic back analysis method[J]. Engineering Mechanics, 1996(Sup1):321-325.

[5] 练继建,马斌,李福田. 高坝流激振动响应的反分析方法[J].水利学报,2007,38(5):575-581.

LIANG Ji-jian, MA Bin, LI Fu-tian.Back analysis algorithm for response of flow-induced vibration in overflow high dam[J]. Journal of Hydraulic Engineering, 2007,38(5):575-581.

[6] 练继建,崔广涛,董淑芳.水工结构流激振动响应的反分析[J].水利水电技术，1998,29(8):51-54.

LIAN Ji-jian, CUI Guang-tao, DONG Shu-fang. Flow-induced vibration back analysis for hydraulic structure[J].Water Resources and Hydropower Engineering, 1998,29(8):51-54.

[7] 王富强，彭新民. 反分析理论在测试结构动应力中的应用[J]. 中国农村水利水电，2008(8):98-103.

WANG Fu-qiang, PENG Xin-min. The application of back analysis theory to the testing dynamic stress of a structure[J]. China Rural Water and Hydropower, 2008(8):98-103.

[8] 彭新民，尚宪峰，杨敏. 基于模态叠加法的弧形闸门流激振动反分析[J]. 中国农村水利水电，2008(1):72-74.

PENG Xin-min, SHANG Xian-feng, YANG Min.Application of mode superposition method in flow-induced vibration counter analysis of arch gate[J].China Rural Water and Hydropower, 2008(1):72-74.

[9] 张建伟,崔广涛,马斌,等.基于泄流响应的高拱坝振源时域识别[J].天津大学学报,2008,41(9):1124-1129.

ZHANG Jian-wei, CUI Guang-tao, MA Bin, et al. Time domain identification of excitation source for high arc dam based on discharge flow vibrationresponse [J]. Journal of Tianjin University, 2008,41(9):1124-1129.

[10] 王海军，练继建，杨敏，等. 混流式水轮机轴向动荷载识别[J]. 振动与冲击，2007,26(4)：123-125.

WANG Hai-jun, LIAN Ji-jian, YANG Min, et al. Identification of axial dynamic load of a francis turbine [J]. Journal of Vibration and Shock, 2007,26(4)：123-125.

[11] 李守巨，刘迎曦，宋树川，等. 基于RBF神经网络的水轮机振源参数识别方法[J]. 大连理工大学学报，2007,47(1)：6-10.

LI Shou-ju, LIU Ying-xi, SONG Shu-chuan, et al. Identification procedure of vibrating load parameters of hydraulic generator with RBF neural network [J].Journal of Dalian University of Technology, 2007,47(1)：6-10.

[12] 常晓通，闫云聚. 一种基于遗传算法的时域内稳态动荷载识别方法[J]. 应用力学学报，2012,29(3)：274-277.

CHANG Xiao-tong, YAN Yun-ju. A genetic algorithm based method for steady-state dynamic force identification in time domain [J]. Chinese Journal of Applied Mechanics, 2012,29(3)：274-277.

Inversion of the whole dynamic displacement field of a prototype high arch dam based on limited points measurement

LI Huo-kun1,2, DENG Bing-mei1, WEI Bo-wen1, HUANG Jin-lin3, FU Xiao4

(1. School of Civil Engineering and Architecture, Nanchang University, Nanchang 330031, China;2. State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China;3. Guangdong Research Institute of Water Resources and Hydropower, Guangzhou 510635, China;4. Huadong Engineering Corporation Limited, Hangzhou 310014, China)

Abstract:The mean square deviation of the dynamic displacement of an arch dam during the flood discharge period is an important indicator for evaluating the intensity of vibration. It is difficult to reflect the distribution characteristics of a whole vibration response field accurately if relying directly on the limited points measurement in dynamic test and also it is not comprehensive and concrete to evaluate the dam vibration safety only with the data measured at limited points. So it is of great significance to inverse the whole dynamic displacement field of the arch dam based on the dynamic response measurement at limited measuring points. Taking the Ertan high arch dam as an engineering example, the dam vibration test under flood discharge excitation was carried out. In accordance with the dynamic displacement responses at limited measuring points arranged on the prototype arch dam, the whole dam dynamic displacement field was inversed by using the genetic algorithm and finite element modal analysis. The specific flow chart of the inversion was provided. The inversion results show that the whole dam dynamic displacement field can be obtained through the dynamic displacement response measurement at only seven measuring points arranged on the top arch of the dam. Simultaneously, the inversion results and the measured values are in good agreement. The method provides a new technique for the reasonable safety assessment of high arch dam during the flood discharge period.

Key words:high arch dam; limited measuring point; prototype vibration test; dynamic displacement response; inverse method

基金项目：国家自然科学基金项目(51269019;51469015;51409139;51569014);天津大学水利工程仿真与安全国家重点实验室开放研究项目(201206);广东省水利科技创新基金项目(2014-08)

收稿日期：2015-05-06修改稿收到日期：2015-06-14

通信作者魏博文 男，博士，副教授，1981年10月生

中图分类号:TV652

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.10.001

第一作者 李火坤 男，博士，副教授，硕士生导师，1981年4月生

E-mail:bwwei@ncu.edu.cn