一种特殊动力吸振器阻抑结构声传递特性分析

林永水, 吴卫国, 甘　进

(1.武汉理工大学 交通学院，武汉　430063; 2.武汉理工大学 理学院,武汉　430070)

一种特殊动力吸振器阻抑结构声传递特性分析

林永水1,2, 吴卫国1, 甘进1

(1.武汉理工大学 交通学院，武汉430063; 2.武汉理工大学 理学院,武汉430070)

摘要：结构声传递控制一直是舰船结构声学设计需要解决的关键问题。动力吸振器是一种重要的波阻技术，具有很好的频段选择性，在舰船的应用日益广泛。针对动力吸振器阻抑板的结构声传递问题，提出了精细的波分析模型和波动力响应矩阵法。将结构离散为多个波导单元和波阻单元，建立附加动力吸振器的结构连接的广义波动力响应平衡方程，推导出波导单元的波动力响应特征矩阵及动力吸振器的附加波动响应特征矩阵，并代入平衡方程求解得到波导单元的振动幅值，从而求得传递效率与损失。数值研究表明动力吸振器在特定频段具有很好的波阻效果，并探讨了动力吸振器设计参数对其波阻特性的影响。研究为动力吸振器的声学设计提供了新的分析方法，在舰船减振降噪中具有重要的理论意义与工程应用价值。

关键词：结构声；传递损失；波分析法；动力吸振器

舰船是板梁组成的空间薄壁结构，阻尼系数低，结构连续性好，是声振动传递的优良导体，因此其结构声传递损失较小。在抑制结构声的传递方面，波阻技术获得了广泛应用，常用的包括阻振质量、黏弹性夹层以及动力吸振器[1-2]。其中阻振质量能有效阻抑高频段结构声的传播，黏弹性夹层在中高频段具有较好的波阻效果，但其会影响结构的强度，不适合主要承力构件结构声传递控制[1]。动力吸振器作为一种重要的波阻技术，其在舰船的应用日益广泛。

国内外对动力吸振器在舰船领域的研究开展了大量工作。Dylejko[3]基于四端参数法和传递功率流研究了安装轴系共振改变器的降噪效果，有效解决了螺旋桨推进过程中引起的纵向推力不平衡，提高了潜艇声隐身性能。李俊等[4-5]采用非线性弹簧设计出了宽频动力吸振器应用于船舶尾部振动控制，并对其参数设计进行了优化研究。杨志荣等[6]提出一种并联安装在船舶轴系上的纵振动力吸振器的设计方法，采用模态截取和模态综合法建立了考虑船舶轴系作为弹性连续体情况下的轴系-动力吸振器混合动力学系统，并探讨了设计参数的影响。以往研究更多是针对杆、梁结构，从振动响应的角度出发，分析单个或多个动力吸振器对结构振动的抑制作用，而从波传播的角度去分析动力吸振器对板的结构声传递阻抑的研究较少。韩彬[7]分析了单个或者多个动力吸振器对结构声波的阻抑作用，认为动力吸振器具有较好的频段选择性，传递损失极大值在共振频率之后取得。车驰东[8]对由连续质量条和弹性层构成的动力吸振器阻抑结构声传递进行了理论分析与数值研究，认为动力吸振器可以克服阻振质量低频效果差的缺陷，传递损失极大值在共振频率取得。

文献[7]只考虑了单个动力吸振器阻抑板的结构声传递特性，文献[8]中多转角的波分析模型忽略近场效应。对于附加动力吸振器的多转角模型，应包考虑每一个动力吸振器的特征参数、布置方式及间距、连接转角及波的近场效应。因此，对多个动力吸振器的阻抑特性，建立更为精细的通用波分析模型，并提出可靠的求解方法，是亟需解决的难题。本文借鉴有限元法思想，参考阻抗法，运用波分析法，建立了精细的波动力分析模型和推导了结构连接的广义波动力响应平衡方程，运用波动力响应矩阵法进行求解。

波动力响应矩阵法用于动力吸振器阻抑结构声传递问题的求解步骤主要如下：

图1　动力吸振器力学分析模型Fig.1 A mechanical analytical model for dynamic vibration absorber

1) 将结构声传播的导体如板、梁、壳等定义为波导元件，对结构声传播起阻碍作用的结构定义为波阻元件，并在结构不连续处(包括波导元件与波阻元件连接，不同的波阻元件连接，不同的波导元件连接)将整个结构离散为多个波导单元和波阻单元。

2 根据连接处变形连续，力与力矩平衡，以波导单元波动力响应和波阻单元的附加波动力响应为状态参数，建立结构连接的广义波动力响应平衡方程。

3) 以波导单元的波动力响应幅值为状态未知量，推导出波导单元的波动力响应特征矩阵及动力吸振器的附加波动响应特征矩阵，代入平衡方程求解得到波导单元的位移响应幅值，进而求出传递效率和传递损失。在此基础上，数值分析动力吸振器设计参数对波阻效果的影响，为其在舰船结构减振降噪的应用提供指导。

1动力吸振器波阻特性理论分析

1.1理论分析模型

如图1(a)左图所示，n+1块平板，其中板i和板i+1(i=1，2，…，n)任意角连接。动力吸振器布置在两板连接处，其由质量条和黏弹性层构成，考虑黏弹性层的弹性作用和阻尼作用，并忽略黏弹性层惯性力的影响，将弹性层等效为阻尼的弹簧系统[8]，如图1(a)右图所示。在板i左端建立局部坐标系，βi+1为板i绕yi+1轴与板重合顺时针所转过的角度。其中，板1和板n+1在x方向为无限长。根据前面定义将结构在不连续处离散为波导单元和波阻单元。

(1)

(2)

弹性波法向入射，角位移、力和力矩(单位宽度)可分别按下式子求解[9]：

(3)

(4)

(5)

(6)

以上推导省略时间简谐因子ejωt。

1.2波动力响应平衡方程

波导单元i和xi=li处的波动力响应分别为PDi和P′Di，其为：

PDi=[uiwiθyiFxiFziMyi]T

(7)

(8)

波阻单元i在xi=li处的波动力响应为P′Ai，其为：

P′Ai=[uAiwAiθAyiFAxiFAziMAyi]T

(9)

根据变形连续，力与力矩平衡，连接处节点有以下平衡方程：

(10)

式中：计算动力吸振器的力与力矩时采用复常数模量模型[10]，ZAxi，ZAzi及ZAθi为质量条与弹性层的串联阻抗，因此有[2]：

ZAxi=ZMxiZKxi/(ZMxi+ZKxi)，

ZAzi=ZMziZKzi/(ZMzi+ZKzi)，

ZAθi=ZMθiZKθi/(ZMθi+ZKθi)

(12)

式中：ZMxi，ZMzi及ZMθi分别表示动力吸振器质量条在 x，z方向的位移-惯性力阻抗及绕y轴转角-惯性力矩阻抗，见式(13)；ZKxi，ZKzi及ZKθi分别表示动力吸振器弹性层在x，z方向的位移-弹性力阻抗及绕y轴的转角-弹性力矩阻抗，根据复常数模量模型[10]，计算公式见式(14)。

ZMxi=ZMzi=(jω)2mAi，ZMθi=(jω)2JAi

(13)

(14)

式中，mAi为动力吸振器i质量条单位长度质量，JAi为其相应的转动惯量；EAi，μAi，lAi，hAi及ηi分别表示黏弹性层i的弹性模量、泊松比、长度、厚度及阻尼损耗因子。

根据式(7)～式(9)，连接处的波动力响应平衡方程为：

(15)

(16)

波导单元与波阻单元的附加波动力响应矩阵存在以下的对应关系：

(17)

将式(17)代入式(15)，得到以波导单元波动力响应为状态变量的结构连接的广义波动力响应平衡方程：

1.3波导单元波动力响应

设波导单元的状态未知量为：

(19)

PDi和P′Di与δi之间存在以下关系：

(20)

(21)

式(20)和(21)中Tdi和T′di为波导单元尺寸特征矩阵，其为对角矩阵，有：

Tdi=diag([111e-jkLilie-jkBilie-kBili])

(23)

T′di=diag([e-jkLilie-jkBilie-kBili111])

(24)

1.4波阻单元附加波动力响应

将式(21)代入式(17)，从而得

(25)

式中：f′DAi为入射波作用于波阻单元i的输入激励。

根据式(10)和(11)，可推导出动力吸振器的附加波动力响应特征矩阵，具体如下：

(26)

式中：ZAxi，ZAzi及ZAθi的计算见式(12)。

1.5输入激励

单位幅值弯曲波和纵波分别法向入射波导单元1时，可用下式表示：

wB1=e-jkB1x1

(27)

uL1=e-jkL1x1

(28)

入射波作用于波导单元的输入激励为：

(29)

f′L1=[10 0 jkL1BL10 0]T

(30)

入射波作用于动力吸振器的输入激励为：

f′BA1=[000-ZRz1-jkB1ZRθ10]

(31)

f′LA1=[000-ZRx100]

(32)

1.6波动力响应平衡方程求解

将式(20)、(21)代入式(18)，得：

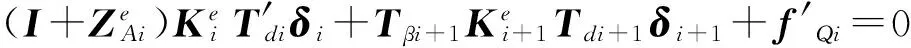
(i=1,2,…,n)

(33)

式中：f′Q1=f′Q1+f′QA1，f′Qi=0,(i=2,…,n)，Q表示入射波，可代表弯曲波和横向剪切波。

对波导单元1和波导单元n+1，有：

(34)

因此把式(33)系数矩阵的前后3列删除，得到矩阵，重新代入式(33)，求解可得到波的幅值。

1.7传递效率与传递损失

假设入射波的幅值为1，入射波，透射波(+)及反射波(-)的输入功率(单位长度板宽)分别为：

Pin=m″iω2cgQi

(35)

(36)

波的传递效率及传递损失分别如下：

(37)

(38)

式中：m″为波导单元的面密度，cgDi代表波群速度，分别cgBi=2cBi,cgLi=cLi。其中cBi，cLi分别表示弯曲波、纵波的相速度。

2动力吸振器波阻特性数值仿真

2.1单级动力吸振器波阻特性

图2所示的为两块15 mm半无限钢板构成120°转角连接处布置动力吸振器的弯曲波传递效率(τ表示透射效率，ρ表示反射效率)。其中动力吸振器质量条的横截面尺寸为100 mm×100 mm，弹性中间层的尺寸为100 mm×50 mm(厚度为质量条的一半)，弹性模量EA=3×109N/mm2，泊松比μA=0.5。图2揭示连接处弯曲波传递效率之和τBB+τBL+ρBB+ρBL=1，满足能量守恒。

图2　附加动力吸振器的弯曲波传递效率(η=0)Fig.2 Transmission efficiency of bending wave of dynamic vibration absorber(η=0)

根据文献[8]，动力吸振器三个自由度上的固有频率分别为：

(39)

根据式(39)求出图2中动力吸振器的固有频率依次为831 Hz，1 518 Hz以及1 073 Hz。图2中弯曲波-弯曲波透射效率τBB并没有在以上相应的共振频率点取得极小值，而是分别在大于fz和小于fθ处取得。在不考虑阻尼的情况下，动力吸振器并不消耗能量，当弹性波的频率等于动力吸振器的固有频率时，根据式(11)，动力吸振器与板连接处的振动位移为零，质量条的位移是一个有限值(与文献[8]中两自由度系统稳态响应相类似)，弯曲波不会全部反射，部分能量传递，τBB不为零。进一步分析可知动力吸振器共振频率点τBB不可能取得极小值，当f=fz时，假如弯曲波发生全反射，τBB取得极小值，那么，板2中的透射弯曲波和近场衰减弯曲波的幅值为0，进而求得板2的线位移、角位移、力与力矩全部为0，联立式(10)，可求得板1中波的幅值，以上求解过程中没有用到力矩平衡方程而得到了板的响应幅值，将求得结果代入力矩平衡方程，发现其不等于0，无法满足力矩平衡条件，在这一假设下，力矩平衡和角位移连续无法同时满足，也就是说当f=fz时发生全反射这一假设不成立，同理，在其他固有频率点也不会发生全反射，部分能量传递过去，因而τBB在共振频率点不可能取得极小值。

以下图3～图10中，分析模型均未考虑阻尼影响，每块钢板厚度均取15 mm，每个动力吸振器的黏弹性层长度和高度分别为100 mm和50 mm，泊松比为0.5。

对图3～图5综合分析，动力吸振器对结构声传递的阻抑在频域上分为两种频段：穿透频段和阻塞频段，其在中间某一频段内具有较为显著的波阻效果。降低动力吸振器的刚度或者增大惯性半径，阻抑频段向低频移动，阻抑带宽将会减小。在进行动力吸振器声学设计时，应根据激励频率，合理选择动力吸振器参数，保证传递损失极大值对应的频率接近激励频率。

以上分析揭示，在共振频率处，动力吸振器对其布置处节点响应的抑制效果达到最佳，但其对波传递的阻抑效果并未达到最佳，传递损失极大值所对应的频率由动力吸振器、板的特性及转角共同决定。

图3 不同弹性模量的动力吸振器弯曲波-弯曲波传递损失Fig.3Bendingwavetransmissionlossofdynamicvibrationabsorberwithdifferentmodulus图4 不同质量和转动惯量的动力吸振器弯曲波传递损失Fig.4Bendingwavetransmissionlossofdynamicvibrationabsorberwithdifferentmassandmomentofinertia图5 不同转角的动力吸振器弯曲波传递损失Fig.5Bendingwavetransmissionlossofdynamicvibrationabsorberwithdifferentcornerangle

2.2周期性多级动力吸振器波阻特性

图6揭示，结构安装多级动力吸振器，传递损失随频率发生振荡，其对结构声的阻抑在频域上分为两种频段：穿透频段和阻塞频段。在穿透频段，传递损失出现“低谷”，达到极小值，当单个动力吸振器的τBB→1时，弯曲波完全通过，其传递损失接近于0，此时平行布置多个动力吸振器的波阻效果与其数量无关；此外，当激励频率接近板的弯曲振动固有频率；弹性波有可能完全穿过，传递损失接近于0。在阻塞频段，动力吸振器级数越多，波阻效果越好。因此，通过改变布置间距，尽量错开结构固有频率与激励频率，使激励频率落入阻塞频段，并增加动力吸振器的级数，能显著提高动力吸振器的波阻效果。

图7给出的是相同参数的两个动力吸振器布置在不同转角连接处的RBB(间距为500 mm)，结果表明，转角为180°的RBB在中间频段的值较其他转角的明显大很多，说明周期性动力吸振器布置在线形连接的波阻效果更佳，因此动力吸振器设计时，最好选择布置在线形连接处，而不是“V”形连接处。

2.3非周期性多级动力吸振器波阻特性

图8和图9分别给出了三个计算模型的弯曲波传递损失RBB，每个模型包括两个动力吸振器，其中实线和单点画线代表不同参数的双级周期性吸振器(两个动力吸振器参数相同)，虚线表示非周期性的双级动力吸振器(两个动力吸振器的参数不同)。图8揭示，不同弹性模量的非周期性双级动力吸振器，其波阻特性将保留低弹性模量吸振器的低频优良阻抑特性和高弹性模量吸振器高频段的优良阻抑特性。图9揭示，不同质量条参数的非周期性双级动力吸振器，其阻抑特性将保留高惯性半径在低频段的优良阻抑特性和低惯性半径在高频段的优良阻抑特性。综合图8和图9，通过选择不同参数的动力吸振器，可增加阻抑频段的选择性，拓宽阻抑频段，提高整个频段的综合波阻效果。不足之处，非周期动力吸振器的难以达到周期性动力吸振器在相应阻塞频段的最大波阻效果。

图10分别比较了三个计算模型的弯曲波传递损失RBB，每个模型包括参数相同的三个动力吸振器，其中实线和虚线分别代表布置间距为250 mm和500 mm的三级周期性吸振器，单点画线表示非周期性的三级动力吸振器(动力吸振器的布置间距l2=250 mm，l3=500mm)。图10表明，动力吸振器非等间距布置，并不会显著增加阻塞频段的传递损失，反而传递损失曲线上出现更多极小值，主要是由于板的共振频率点增加；但其在共振频率点的传递损失极小值较周期性动力吸振器的显著增大，也就是说非周期性布置会增加共振穿透频段的阻抑效果。

图6 多级周期性动力吸振器的弯曲波传递损失比较Fig.6Comparisonofbendingwavetransmissionlossofseveralparallelingdynamicvibrationabsorbers图7 不同转角的双级动力吸振器的弯曲波传递损失比较Fig.7Bendingwavetransmissionlossoftwo-stagedynamicvibrationabsorberswithdifferentcornerangle图8 不同弹性模量的双级动力吸振器弯曲波传递损失Fig.8Bendingwavetransmissionlossoftwo-stagedynamicvibrationabsorberswithdifferentelasticmodules

图9　不同质量与转动惯量的双级动力吸振器的弯曲波传递损失Fig.9 Bending wave transmission loss of two-stage dynamic vibration absorbers with different mass and moment of inertia

图10　不同布置间距的多级动力吸振器的弯曲波传递损失Fig.10 Bending wave transmission loss of multistage dynamic vibration absorbers with different layout interval

以上分析表明，采用非周期性多级动力吸振器，合理选择不同的黏弹性层参数(弹性模量、长度及高度等)、质量条参数(质量、转动惯量)以及改变布置间距与方式，可提高穿透频段的波阻效果，拓宽阻抑频段。

3结论

(1) 研究为动力吸振器阻抑板的结构声传递提供了一种新的分析方法，并且适用于周期性和非周期性多级动力吸振器的波阻特性分析，简单且便于理解，简化了求解过程，提高了分析效率。

(2) 增大质量条的惯性半径，减小黏弹性层的弹性模量或长度以及增大其高度，可提高中低频段的波阻效果；通过改变布置间距及方式，可提高特定频段的波阻效果。动力吸振器布置在线形连接处，更能发挥其波阻作用；增加周期性动力吸振器的级数可提高阻塞频段的波阻效果；对非周期性多级动力吸振器，选择不同的设计参数，拓宽波阻频段，可提高穿透频段的波阻效果。

(3) 动力吸振器在某一特定频段具有显著的波阻效果，与阻振质量相比，重量显著降低，特别适用于船舶动力舱段的结构声传递控制，在民用船舶上具有广阔的应用前景。

参 考 文 献

[1] Cremer L, Heckl M, Ungar E E. Structure-borne Sound[M].3rd.ed. Berlin: Springer-Verlag, 2005.

[2] 阿斯尼基福罗夫. 船舶结构声学设计[M]. 北京：国防工业出版社，1998.

[3] Dylejko P G. Optimum resonance changer for submerged vessel signature reduction[D]. Sydney:Australia University of New South Wales, 2007．

[4] 李俊，金咸定，王宏. 减小船体艉部振动的动力吸振器研究[J]. 中国造船，2001, 23(2): 99-101．

LI Jun, JIN Xian-ding, WANG Hong. Research on dynamic absorber for reducing vibration of ship stern[J]. Shipbuilding of China, 2001, 23(2): 99-101.

[5] 李俊，金咸定. 动力吸振器的宽带数值优化设计[J]. 振动与冲击, 2001, 20(2): 18-20.

LI Jun, JIN Xian-ding. Numerical optimal design for broadband dynamic absorber[J]. Journal of Vibration and Shock, 2001, 20(2): 18-20.

[6] 杨志荣，秦春云,饶柱石，等. 船舶推进轴系纵振动力吸振器设计及参数影响规律研究[J]. 振动与冲击,2012,31(16): 48-52.

YANG Zhi-rong, QIN Chun-yun, RAO Zhu-shi,et al. Design and analysis of a dynamic absorber for reducing axial vibration of ship shafting[J]. Journal of Vibration and Shock, 2012, 31(16): 48-52.

[7] 韩彬. 基于动力吸振器的结构声传递抑制[D]. 武汉：华中科技大学，2006.

[8] 车驰东. 动力设备结构声传递的理论分析及阻波技术的研究[D]. 上海：上海交通大学，2008.

[9] Kessissoglou N J. Power transmission in L-shaped plates including flexural and in-plane vibration[J]. Journal of the Acoustical Society of America, 2004, 115(3): 1157-1169.

[10] 李军强，刘宏昭，王忠民. 线性粘弹性本构方程及其动力学应用研究综述[J]. 振动与冲击, 2005, 24(2): 116-123.

LI Jun-qiang, LIU Hong-zhao, WANG Zhong-min. Review on the linear constitutive equation and its dynamicsapplication to viscoelastic materials[J].Journal of Vibration and Shock, 2005, 24(2): 116-123.

New method for impeding structure-borne sound transmission by using a special dynamic absorber

LIN Yong-shui1,2, WU Wei-guo1, GAN Jin1

(1. School of Transportation, Wuhan University of Technology, Wuhan 430063, China;2. School of Science, Wuhan University of Technology, Wuhan 430070, China)

Abstract:The control of structure-borne sound transmission is a key problem to be solved in acoustic design of marine structure. Dynamic vibration absorber is one of the very important wave blocking techniques and has good frequency selectivity, which is widely used in naval ships. A fine theoretical model and a corresponding wave dynamic response matrix method were put forward to investigate the impeding of structure-borne sound transmission by using a dynamic absorber. The structure was discretized into many wave guide elements and wave resistance elements and a general wave dynamic response equilibrium equation for the junction of the attached dynamic absorber was developed. The wave dynamic response matrices of wave guide elements and the added wave dynamic response matrices of wave resistance elements were deduced. The vibration amplitudes of wave elements were obtained by resolving the equilibrium equation and the transmission efficiency and transmission loss were then calculated. The method was illustrated by a series of wave attenuation models with different design parameters. The numerical computation results show that the wave transmission loss in a specific frequency band will be greatly improved. The research work provides a new analysis method for the acoustic design of dynamic vibration absorber, which has great theoretical significance and is of important value for the noise and vibration reduction on board.

Key words:structure-borne sound; transmission loss; wave analysis; dynamic vibration absorber

基金项目：国家高技术船舶计划(2015)

收稿日期：2015-03-25修改稿收到日期：2015-09-08

通信作者甘进 男，博士，讲师，1982年2月生

中图分类号:U661；U666；TB535

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.10.035

第一作者 林永水 男，博士，讲师，1983年11月生

E-mail :ganjin@whut.edu.cn