考虑断丝影响的平行钢丝索拉伸力学特性

张婷婷,谢　旭,潘骁宇

(浙江大学 土木工程系,浙江 杭州 310058)



考虑断丝影响的平行钢丝索拉伸力学特性

张婷婷,谢旭,潘骁宇

(浙江大学 土木工程系,浙江 杭州 310058)

摘要:为了分析断丝对平行钢丝索拉伸力学特性的影响，提出考虑钢丝间摩擦影响的纤维束计算模型.通过对3种不同高度索段试件顶推试验获得钢丝间的摩擦力特性，应用提出的纤维束计算模型分析钢索拉伸时断丝引起的内力重分布规律，讨论钢丝间的摩擦作用对断裂钢丝的张力恢复以及钢索承载能力等特性的影响.顶推试验结果表明，高度10 cm的平行钢丝索段试件，钢丝间的单位长度摩擦刚度均值为0.192 kN/mm2，单位长度滑动摩擦力均值为0.022 kN/m； PE套管的握裹力不会沿索截面的径向传递；理论计算结果表明，考虑钢丝间摩擦影响时，断裂钢丝的张力离开断口约1.5～2.0 m后线性恢复到断丝前的大小；考虑钢丝间摩擦影响的钢索承载能力略大于忽略摩擦影响的值；在断丝截面，未断裂的钢丝较均匀地分摊断裂钢丝释放的张力.

关键词：平行钢丝索；摩擦力试验；断丝；内力重分布；极限承载力

由Weibull等[1]提出并经Daniels[2]完善的纤维束理论是计算平行钢丝索拉伸强度的常用方法.这种算法是将钢丝束离散成串并联单元,即所有钢丝互相并联,每根钢丝的强度由串联钢丝单元中最薄弱单元决定的计算方法.迄今为止,不少学者基于纤维束理论计算平行钢丝索的极限强度.如Matteo等[3]用Monte-Carlo方法模拟钢丝力学参数的随机性,根据极值分布理论评估了Williamsburg桥主缆的残余承载能力.Haight等[4]采用钢丝延性模型和延脆性模型分析了钢丝长度对索极限强度的影响.Cremona等[5]从钢丝样本的拉伸试验结果计算钢索的极限强度.朱劲松等[6]用Matteo的延脆性模型以及Monte Carlo随机仿真分析模拟钢丝力学特性,用纤维束理论确定拉索强度,并讨论了Daniels效应中钢丝数目与平均钢丝强度关系.徐俊等[7-11]根据钢索内锈蚀分布规律定义腐蚀钢丝力学特性,提出平行钢丝索的承载力计算方法,并分析吊杆抗力衰减规律.

然而,传统的纤维束理论不考虑钢丝之间的摩擦影响,断丝发生后即让该钢丝退出工作.实际钢索由于磨损、锈蚀、疲劳、初缺陷等原因使得钢丝间的使用寿命不同,先断裂的钢丝在应力释放过程中由于钢丝间摩擦改变钢索内其他钢丝的应力分布.为了研究这种影响,李元兵[9]通过理论推导以及有限元计算方法分析了钢绞线索钢丝脆断后的截面内力分布规律.彭崇梅等[12-13]以半平行钢索为对象,假定钢索的握裹力沿着钢索径向传递,建立静力拉伸荷载下对称断丝及非对称断丝模型,从力的平衡关系分析了断丝时钢丝的应力分布规律,并得到断丝拉力随离开断口距离增加呈线性增加的结论.但是,以上计算采用的摩擦系数以及握裹力的传递方向假定缺乏依据,研究结论有待试验的验证.

根据上述情况,本文首先通过试验方法研究钢丝间的摩擦特性,在此基础上建立考虑摩擦影响的纤维束计算模型.通过平行钢丝索断丝情况下各钢丝应力分布以及钢索的极限拉伸强度等力学性能分析,研究钢丝间摩擦对服役吊杆断丝时的力学性能影响.

1服役钢索的钢丝间摩擦力试验研究

1.1钢丝间摩擦力试验方法

为了评价钢丝间的摩擦特性,本文从服役了17 a的拱桥吊杆中截取试件,通过钢丝顶推试验测试平行钢丝索的钢丝间摩擦特性.吊杆截面由109根直径5 mm的平行钢丝组成,钢丝表面有轻度锈迹.为了比较试件高度的影响,在同一吊杆中截取10、15和20 cm 3种不同高度的索段作为试验对象.

如图1所示为钢丝顶推试验方法以及中心钢丝顶推完成后的状况.钢丝顶推设备采用微电子万能试验机(WDW-I00E),在试验机上下端分别安装了顶杆和预设小孔的光面钢板(垫板),顶杆对准待顶推的钢丝让其在底部的小孔中通过,而其他钢丝不发生位移.受到实验条件的限制,单次顶推量设置为4 mm.

图1　试验装置以及中心钢丝顶推后的索段状况Fig.1　Experimental device and tested status of segment samples

1.2试验结果

选取不同层的钢丝进行顶推试验.被顶推钢丝其层数位置如图2所示.钢丝由内向外分为6层,每层任意选取2根钢丝作为顶推对象.

图2　顶推试验的钢丝层数分布Fig.2　Layer distribution of testing wires

如图3所示为典型的非外层以及外层钢丝顶推试验荷载(Fs)-位移(D)曲线,结果取自高度20 cm的试件.其中,非外层钢丝为截面第4层钢丝,外层钢丝为截面第6层钢丝.由图3可知,对于非外层钢丝,顶推荷载随着滑移位移的增大呈线性增加,至峰值附近时其上升趋势变缓,达到峰值后外荷载随位移增大而逐渐下降,最后逐渐趋于稳定；而直接与热塑型PE套管接触的外层钢丝,其荷载位移曲线在在峰值附近由于PE套管对钢丝的黏滞作用产生一个小的波折,然后随着顶推量的增加而缓慢下降,直至趋于稳定.外层钢丝的下降段斜率明显低于非外层的钢丝,内层钢丝荷载峰值相对外层钢丝较高,表明PE套管与钢丝间的摩擦特性跟钢丝之间的摩擦特性有明显的差异.

图3　内外层钢丝顶推试验结果对比一例Fig.3　Load-displacement curve for two samples

钢丝顶推试验荷载位移曲线的上升段和下降段斜率通过线性拟合得到,曲线上升段为荷载从0逐渐增加至峰值的区段；下降段为荷载从峰值逐渐下降至稳定值的区段,其中外层钢丝的下降段不包括波折区间,即图3中位移D=0.6～4.0 mm的结果.由于试验结果得到的下降段斜率不是恒定的值,本文采用线性拟合的方式得到其平均值,以15 cm试件第3层钢丝为例,其线性拟合结果见图4.

图4　线性拟合结果一例Fig.4　Linear fitting curve for sample

如表1所示为钢丝顶推试验结果，表中的摩擦刚度及摩擦力均换算为钢丝单位长度的结果.由于顶推力是钢丝的总摩擦力,这里假定索段长度范围内的摩擦力相同,取实测的总摩擦力与试验索段长度、摩擦接触面数的比值作为钢丝单位长度的摩擦力.当样本高度较小时,摩擦力均匀分布的假定所引起的误差可以近似忽略.另外,试验钢丝“2-2”表示其截面第2层钢丝的第2个样本,层数编排参见图2；Fp为单位长度荷载峰值,其物理意义为单位长度滑动摩擦力；K1,K2分别为曲线上升段和下降段斜率与试件高度的比值,其物理意义为单位长度摩擦刚度.其中,符号“*”表示外层钢丝.

表1　钢丝顶推试验结果

由表1可知,单位长度滑动摩擦力及摩擦刚度与试件高度有一定关系,高度h=10 cm的试件结果略高于其他2个试件，单位长度摩擦刚度在0.163～0.209 kN/mm2之间波动,均值为0.192 kN/mm2,单位长度滑动摩擦力在15.48～34.38 kN/m之间变化,均值为22.22 kN/m；高度15和20 cm试件的单位长度摩擦刚度均值分别为 0.097、0.110 kN/mm2,单位长度滑动摩擦力均值分别为14.73、20.22 kN/m.对于同一高度的试件,单位长度滑动摩擦力以及单位长度摩擦刚度与所在的钢丝层位置并没有明显的关系,表明钢丝排序的方式使得截面结构稳定,钢丝间的握裹力并非沿着径向传递.

2考虑摩擦影响的纤维束计算模型

图5　纤维索计算模型Fig.5　Analytical model based on theory of bundles of threads

如图5(a)所示为考虑钢丝间摩擦影响的纤维束计算模型.其中,平行钢丝索沿长度L方向均匀划分成若干段,索段长度为L0,n为划分的索段数.单根钢丝由钢丝单元纵向串联连接,不同钢丝之间相互并联；截面上相邻钢丝节点之间引入摩擦单元传递摩擦力,非相邻单元之间没有力的传递关系.为了表述方便起见,钢丝编号顺序按如图5(b)所示的方式,截面由中心层向外分层编号,每层钢丝的编号由x轴位置开始沿逆时针方向从小到大编排,并按层连续.钢丝单元编号按索段顺序从上至下连续增加,其最大编号由分段数决定.

图6　钢丝及摩擦单元的材料特性Fig.6　Material properties of wire and friction element spring

钢丝单元和摩擦单元采用如图6所示的双直线模型,其中摩擦力假定为理想弹塑性关系.图中,E1、E2分别表示钢丝屈服前后的弹性模量,εe、εu分别表示钢丝单元屈服应变以及极限应变,σe、σu分别表示钢丝单元屈服应力以及极限应力；δy、Fy分别表示弹簧单元由静摩擦力转为动摩擦力的相对位移和拉力.

为模拟吊杆在服役过程中钢丝力学特性退化的不均匀性及随机性,采用Monte Carlo法对所有钢丝单元的截面积及极限应变在规定的参数范围内按预先设定的概率模型随机生成.其中,摩擦单元的滑动摩擦力取试验结果中Fs-D曲线的峰值和强制位移达4 mm之间下降段的平均值来近似.另外,因顶推试验不能测试钢丝沿试件高度的摩擦力分布规律,得到的荷载-位移均为钢丝端部的结果.因此,计算选取结果较稳定,高度对其影响较小的10 cm高度索段的摩擦参数.

如图7所示为钢索极限承载能力的计算框图,荷载通过在钢索一端施加强制位移的方法实现.在加载过程中,当钢丝的拉伸应变达到极限应变时,对应的单元退出工作,通过计算新的平衡来确定断丝后的应力重分配.非线性计算采用Newton-Raphson迭代方法.

图7　钢索承载能力计算框图Fig.7　Flow chart for ultimate strength analysis of cables

3算例及结果分析

3.1计算参数

传统纤维束理论不考虑钢丝间的摩擦作用,认为钢丝发生断裂即退出工作,不再具备承载能力.为了分析平行钢丝索断丝时的内力分布规律及力学特性变化,本文采用图5所示的纤维束计算模型及试验取得的钢丝间摩擦特性结果,以一根长度5 m,截面由37根直径5 mm平行钢丝组成的吊杆为例进行分析.钢丝的屈服应力和极限应力分别为1 580、1 700 MPa，初始张力为70 kN.

3.2特定钢丝断裂后的钢索内力重分布

为了分析平行钢丝索特定钢丝断丝后的内力重分布,定义其中一个钢丝单元的截面面积小于其他钢丝单元,使其首先达到极限应变而发生断裂.为了保证钢索在张拉过程中其他钢丝不发生断裂,不妨设该特定单元的截面积为其他钢丝单元的90%.

为了分析断口位置的钢丝内力重分布,分别对中心层1号钢丝、外2层8号钢丝的中间单元截面积进行折减.如图8所示为中心钢丝断裂前后中心钢丝以及断丝截面上其他钢丝的张力变化.其中,T为钢丝单元张力,l为钢丝单元轴向位置,m为钢丝编号.由图8可知,中心钢丝断丝后其张力沿着钢丝轴向呈现线性恢复,距离断口1.5 m时钢丝张力恢复至断丝前水平的85.41%；距离断口2 m左右时,张力恢复至断丝前水平.与此相对应,周围相邻钢丝的张力呈线性上升,在断丝截面增幅最大,为断丝前的102.62%,即断丝损失的部分应力由周围的钢丝均匀分担,分担比例与钢丝的位置无明显关系.

图8　中心钢丝断丝后内力重分布Fig.8　Redistribution of wire axial force after central wire breaks

为了分析中心钢丝断丝后的内力重分布机理,对中心1号钢丝与相邻2号钢丝的相对位移进行了分析,断丝后选取2个状态进行比较，结果如图9所示.其中,纵坐标d分别表示1、2号钢丝相邻节点的相对位移.由图9可知,断丝前的节点相对位移较小,仅在面积削弱单元附近产生；断丝后,由于断丝钢丝回缩变形导致相对位移增大,并沿着轴向递增,距离断口1.3 m后相对位移趋于稳定.后随着强制位移的逐渐增大,其他钢丝相继发生断裂,1、2号钢丝之间的相对位移也逐渐增大.

图9　断丝前后同截面相邻节点相对位移Fig.9　Relative displacement of nodes in cross-section

图10　8号钢丝断丝后内力重分布Fig.10　Redistribution of wire axial force after 8th wire breaks

如图10所示为外2层8号钢丝断丝后的内力分布图.由图10可知,外层钢丝断丝后其张力沿着钢丝轴向呈线性恢复,距离断口1.5 m后钢丝的张力恢复至85.40%；距离断口2 m左右时张力恢复至断丝前水平.同时,与断丝钢丝相邻的5号钢丝张力呈线性上升,最大增至断丝前的102.59%左右,与中心钢丝断裂时的内力分布规律基本相同.

由以上结果可知,断裂钢丝的张力恢复水平并不受钢丝位置的影响,断丝后虽然与此直接相邻的钢丝张力略高于其他钢丝,但差异不明显.

3.3随机断丝时的钢索力学特性

锈蚀、磨损、疲劳、初缺陷等均会引起钢丝单元之间的力学性能存在差异.本文以锈蚀作为钢丝单元力学性能变化的原因,分析钢索随机断丝情况下的拉伸力学特性.假定钢索的锈蚀等级为文献[14]定义的Ⅲ级,这时钢丝的有效截面积损失范围为0.5%～2%,延性折减范围为5%～15%.在上述参数范围内,通过Monte Carlo法随机对钢丝单元的力学特性进行赋值,确定各单元的极限应变及截面参数.采用图7所示的模型计算框图对钢索随机断丝条件下的内力重分布及极限承载能力进行分析.

如图11所示分别为37、61根Φ5 mm直径钢丝组成的平行钢丝索断丝后的钢丝应力分布图.由图11(a)可知,由37根钢丝组成的平行钢丝索23号钢丝在距离端部1.2 m处首先发生断裂,断丝后断丝钢丝张力沿着轴向线性恢复,距离断口1.2 m以及3.8 m时,张力分别恢复至断丝前水平的36.71%和96.73%；随着端部强制位移的增加,相邻的22号钢丝在同一截面上发生断裂.由图11(b)可知,当钢丝根数为61根时,26号钢丝在中部首先发生断裂,断丝后断丝钢丝张力随距离线性恢复,距离断口1.6 m左右恢复至断丝前水平；之后58号钢丝在靠近端部发生断裂；随着强制位移增加,45号钢丝在26号断丝截面上发生断裂.

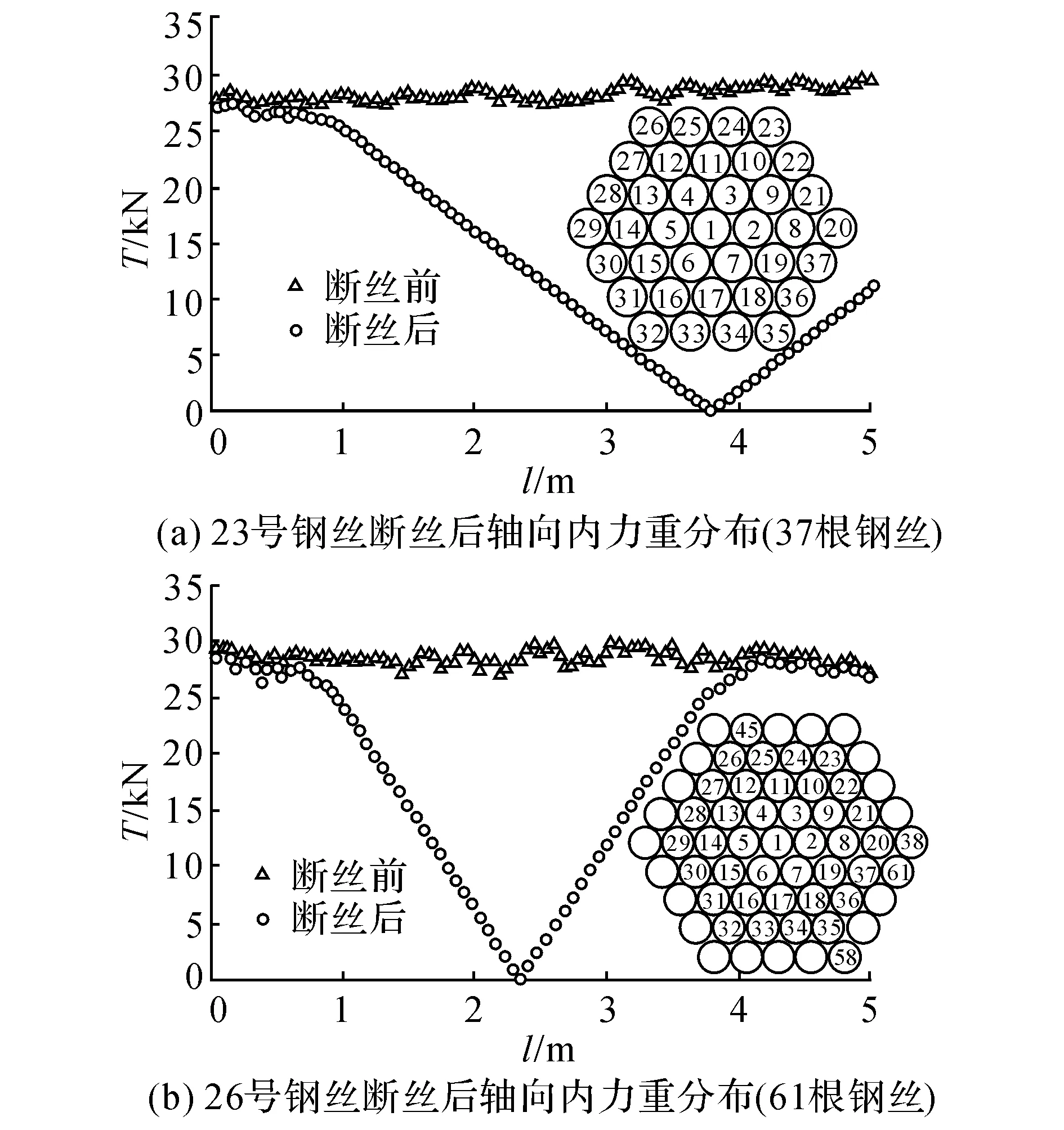
图11　钢丝在断丝前后沿轴向的内力分布Fig.11　Distribution of broken wire axial forces after/before breaks

如表2所示为不考虑钢丝间摩擦作用和考虑摩擦作用时纤维束计算模型当断丝率达到5%时的钢索承载能力Fb计算结果,钢索的锈蚀等级仍假定为Ⅲ级.由表2可知,当平行钢丝索钢丝数量为37根时,考虑摩擦影响的平行钢丝索承载能力比不考虑摩擦影响的结果增加了2.16%；钢丝数目为61根时,其5%断丝率的承载能力增加了3.15%.因此,钢丝间的摩擦力对平行钢丝索的承载能力影响比较小.

表2摩擦对钢索承载能力的影响

Tab.2Effect of inter-wire friction on cable ultimate strength

钢丝数目断丝数目是否考虑摩擦Fb/kN372是994372否973613是1660613否1610

4结论

根据平行钢丝索钢丝间摩擦力试验以及考虑摩擦影响的纤维束模型计算理论分析结果,得到以下结论：

(1) 平行钢丝索的钢丝间摩擦力特性与钢丝所在的位置没有明显关系,可以认为PE套管的径向压力不会沿着钢索截面径向传递；

(2) 当试件高度为10 cm时,其单位长度平均摩擦刚度为0.163～0.209 kN/mm2,均值为0.192 kN/mm2；单位长度平均滑动摩擦力为0.019～0.025 kN/mm,均值为0.022 kN/m.这些参数随着试件高度增加而降低；

(3) 钢丝间摩擦力超过峰值后呈下降变化；

(4) 断丝后由于内力重分布,剩余钢丝较均匀地分担断丝钢丝的张力；断丝后随着离断口的距离增加,张力沿轴向呈线性恢复,其张力恢复不随断丝钢丝所在的位置变化而变化；

(5) 以锈蚀钢索断丝率达到5%的作为极限状态,比较了钢丝间摩擦力对钢索承载能力计算结果的影响.结果表明当考虑摩擦影响时,钢索拉伸承载能力计算结果略大于不考虑摩擦影响的值.

参考文献(References)：

[1]WEIBULL W. A statistical representation of fatigue failures in solids [M]. Goteborg: Elanders Boktryckeri Aktiebolag, 1949:5-12．

[2]DANIELS H E. The statistical theory of the strength of bundles of threads [J]. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 1945, 183(995): 405-435．

[3]MATTEO J, DEODATIS G, BILLINGTON D P. Safety analysis of suspension-bridge cables: Williamsburg Bridge [J]. Journal of Structural Engineering, ASCE, 1994, 120(11): 3197-3211．[4]HAIGHT R Q, BILLIONGTON D P, KHAZEM D. Cable safety factors for four suspension bridges [J]. Journal of Bridge Engineering, ASCE, 1997, 2(4):157-167．

[5]CREMONA C. Probabilistic approach for cable residual strength assessment [J]. Engineering Structures, 2003, 25(3): 377-384．

[6]朱劲松,肖汝诚. 大跨度斜拉桥拉索安全性分析方法研究[J]. 土木工程学报, 2006, 39(9): 74-79．

ZHU Jin-song, XIAO Ru-cheng. A study on the safety assessment method for stay cables of long-span cable-stayed bridges [J]. China Civil Engineering Journal. 2006, 39(9): 74-79．

[7]徐俊. 拉索损伤演化机理与剩余使用寿命评估[D]. 上海：同济大学, 2006: 98-111．

XU Jun. Damage evolution mechanism and remained service lives evaluation of stayed cables [D]. Shanghai: Tongji University, 2006: 98-111．

[8]徐宏. 桥梁拉 (吊) 索损伤后力学分析及安全评价[D]. 西安: 长安大学, 2008: 90-119．

XU Hong. Mechanical analysis and safety evaluation of bridge damaged cable [D]. Xi’an: Xi’an University, 2008: 90-119.

[9]李元兵. 拱桥吊杆力学行为及损伤退化研究[D]. 上海: 同济大学, 2008．

LI Yuan-bing. Research on mechanical behavior and damage deterioration of suspender for arch bridges [D]. Shanghai: Tongji University, 2008．

[10]兰成明,平行钢丝斜拉索全寿命安全评定方法研究[D]. 哈尔滨：哈尔滨工业大学, 2009: 102-129．

LAN Cheng-ming. Study on life-cycle safety assessment methods for parallel wire stay cable [D]. Harbin: Harbin Institute of Technology, 2009: 102-129.[11]高欣. 在役钢管混凝土拱桥吊杆损伤与系统可靠性分析方法[D]. 哈尔滨: 哈尔滨工业大学, 2011: 97-102．

GAO Xin. Analysis methods for suspender damage and system reliability of existing concrete filled steel tubular arch bridge. Harbin: Harbin Institute of Technology, 2011: 97-102．

[12]彭崇梅, 张启伟, 李元兵. 桥梁半平行钢丝索的对称断丝损伤力学模型[J]. 同济大学学报: 自然科学版, 2013, 41(1): 20-26．PENG Chong-mei, ZHANG Qi-wei,LI Yuan-bin. Damage model of multilayered semi-paralleled wire cables for bridges with symmetric wire breaks [J]. Journal of Tongji University:Natural Science, 2013, 41(1): 20-26．[13]彭崇梅, 张启伟, 李元兵. 桥梁半平行钢丝索对称断丝的力学特性分析[J]. 同济大学学报：自然科学版, 2013, 41(4):496-502. PENG Chong-mei, ZHANG Qi-wei, LI Yuan-bin. Mechanical properties analysis of semi parallel wire cables for bridge with symmetric wire breaks [J]. Journal of Tongji University ：Natural Science, 2013, 41(4): 496-502．[14]潘骁宇,谢旭,李晓章,等. 锈蚀高强度钢丝的力学性能与评级方法[J].浙江大学学报：工学版, 2014, 48(11): 1917-1924．

PAN Xiao-yu, XIE Xu, LI Xiao-zhang et al. Mechanical properties and grading method of corroded high-tensile steel wires [J]. Journal of Zhejiang University ：Engineering Science, 2014, 48(11): 1917-192.

Tensile mechanical behavior of parallel wire cables with wire breaks

ZHANG Ting-ting, XIE Xu, PAN Xiao-yu

(DepartmentofCivilEngineering,ZhejiangUniversity,Hangzhou310058,China)

Abstract:In order to analyze the tensile mechanical behavior of the parallel wire cables with broken wires, an analytical model based on the theory of bundles of threads was presented considering the effect of inter-wire friction. By laboratory test for three segment samples in different lengths extracted from parallel wire cables, the friction characteristics between wires in different layers were gained as input variables in the analytical model. This paper studied the stress redistribution of wires in cable due to wire breaks, and discussed the recovery tensile force of the broken wire, and the ultimate strength of the cable when considering the inter-wire friction. Laboratory test results showed from the segment in length of 10cm, that the average friction rigidity of unit length is about 0.192 kN/mm2, and the average friction resistance is 0.022 kN/mm. The wrapping force of the PE casing was not transmitting in the radial direction of cable crosssection. The theoretical calculation results showed that the tensile force of broken wires grew linearly with the distance from the breaking point, and the recovery length is about 1.5 m to 2.0 m due to the inter-wire friction. The ultimate strength of cable increased slightly compared to those without considering the inter-wire friction, and on the cross-section of the breaking point, the other wires shared the tensile force of the broken ones evenly.

Key words:parallel wire cables; laboratory test; wire breaks; redistribution of wire axial force; ultimate strength of cable

收稿日期：2015-06-17.浙江大学学报(工学版)网址： www.journals.zju.edu.cn/eng

基金项目：国家自然科学基金资助项目(51378460).

作者简介：张婷婷(1989-)，女，硕士生，从事拱桥吊杆损伤等研究. ORCID: 0000-0001-6729-0207. E-mail: 3090103176@zju.edu.cn通信联系人：谢旭，男，教授. ORCID: 0000-0002-4247-0487. E-mail: xiexu@zju.edu.cn

DOI:10.3785/j.issn.1008-973X.2016.05.005

中图分类号：U 443.38

文献标志码：A

文章编号：1008-973X(2016)05-0841-07