钢管混凝土组合桥墩变形能力计算模型
王 震,王景全,2,戚家南
(1. 东南大学 混凝土及预应力混凝土结构教育部重点实验室,江苏 南京 210096;2. 东南大学 国家预应力工程技术研究中心,江苏 南京 210096)
钢管混凝土组合桥墩变形能力计算模型
王震1,王景全1,2,戚家南1
(1. 东南大学 混凝土及预应力混凝土结构教育部重点实验室,江苏 南京 210096;2. 东南大学 国家预应力工程技术研究中心,江苏 南京 210096)
摘要:为准确预测钢管混凝土组合(CFSTRC)桥墩的变形能力,提出考虑剪切和纵筋滑移影响的计算模型. 该模型基于纤维模型计算结果,考虑P-Δ效应,将桥墩变形分为弯曲变形、剪切变形和纵筋滑移变形3部分,分别采用塑性铰模型、压弯剪耦合作用分析方法及纵筋滑移模型计算桥墩的弯曲变形、剪切变形和纵筋滑移变形. 利用计算模型与塑性铰模型对3根已知试件分别进行计算,建议模型计算结果与试验值吻合较好,塑性铰模型不能考虑剪切变形影响,计算结果较试验值偏小. 结果表明:CFSTRC桥墩在轴压力和水平荷载共同作用下的剪切变形不容忽视;利用建议模型能够得到CFSTRC桥墩在压剪弯共同作用下的非线性变形全过程,结果可信,可用于CFSTRC桥墩的变形计算.
关键词:桥墩;钢管混凝土;剪切变形;纵筋滑移;纤维模型
钢管混凝土组合(concrete filled steel tube reinforced concrete,CFSTRC)结构是由截面中部的钢管混凝土和钢管外的钢筋混凝土组合而成,它具有延性好、施工方便和抗火性能好等优点. 利用这一组合结构代替传统的钢筋混凝土(reinforced concrete,RC)结构用于震区桥墩,不仅可以放宽规范对纵筋用量和轴压力的限制[1],同时也可以有效解决因在塑性铰区配置大量箍筋而造成的混凝土浇筑质量差等问题[2],具有良好的应用前景.
目前,关于CFSTRC墩柱抗震性能的研究还相对较少. 李惠等[3]利用条带法对方套圆截面弯矩-曲率关系进行了计算;钱稼茹等[4]通过试验研究了轴压比和配箍特征值的影响;韩林海等[5]报道了方套方、方套圆和圆套圆等不同截面CFSTRC墩柱的抗震性能;廖飞宇等[6]利用Abaqus有限元模型对CFSTRC墩柱的滞回性能进行了数值模拟;纪晓东等[7]通过拟静力试验研究了墩柱的滞回性能和位移延性,并借助OpenSees有限元模型进行了数值分析. 综上所述,对CFSTRC墩柱抗震延性的研究仍以试验和有限元模拟为主,尚缺少可行的理论方法用于计算CFSTRC墩柱的变形能力. 而基于性能的桥墩抗震设计和评价方法都选择变形作为设计和评价的指标,这些方法的实现都依赖于对桥墩变形的准确预测[8].
本文提出的CFSTRC桥墩变形计算模型以截面弯矩-曲率关系为基础,计入P-Δ阶效应,以塑性铰模型计算弯曲变形,利用压剪弯耦合作用(axial-shear-flexure interaction, ASFI)分析方法[9-10]计算剪切变形,考虑纵筋滑移变形影响,计算过程满足力的平衡条件与变形协调. 利用已有试验资料对建议模型进行验证,并将建议模型结果与传统的塑性铰模型结果进行比较.
1截面纤维模型
1.1计算方法
1.1.1基本假设平截面假定,即截面应变沿高度线性分布;不考虑钢筋、钢管与混凝土之间的相对滑动;不考虑混凝土收缩和徐变的影响.
1.1.2计算原理如图1所示,截面分为纵筋、无约束混凝土和箍筋约束混凝土、钢管和钢管约束混凝土5种纤维,每一个纤维用各自中心处的应变作为平均应变. 在截面形心处作用一个不变的轴压力p,对一个给定截面曲率φi,采用区间搜索法[11]确定其相应的中性轴深度xn,考虑平截面假定及材料本构关系,可以确定出截面应变、应力分布,对全截面进行积分即可获得相应的截面抵抗弯矩M.

图1 钢管混凝土组合桥墩截面纤维模型Fig.1 Fiber model of cross section of concrete filled steel tube reinforced concrete bridge column
1.2材料本构


图2 纤维模型选用的材料本构关系Fig.2 Constitutive relations of materials used by fiber model
1.3纤维模型计算结果的试验验证
选择文献[5]中试件SS1、试件SS2和试件SS3分别建立纤维模型计算截面弯矩-曲率曲线(M-φ曲线),并将纤维模型结果与试验值进行比较,如图3所示,从图3中可以看出3根试件的计算结果都与试验值吻合得较好,说明利用纤维模型计算截面M-φ曲线的方法可行.

图3 纤维模型结果与试验值对比Fig.3 Comparison of results of fiber model and trial values
2计算桥墩变形的建议模型
为方便计算,本节中变形均以墩顶水平位移Δ与剪跨长度L之比即位移角γ表示,并规定应力应变符号以受拉为正,受压为负.
2.1弯曲变形计算
如图4所示为塑性铰模型假定的桥墩曲率分布:受拉钢筋屈服前桥墩不同截面的曲率沿墩高呈线性变化;受拉钢筋屈服后桥墩下端形成塑性铰,塑性铰区段内塑性曲率均匀分布[15].
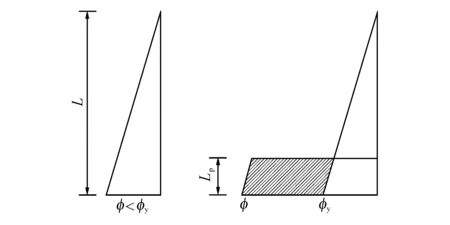
图4 桥墩的曲率分布Fig.4 Curvature distributions for bridge columns
(1)
式中:L为桥墩剪跨长度;φy为受拉钢筋屈服时截面曲率,σs为受拉钢筋应力,fsy为受拉钢筋屈服强度,Lp为等效塑性铰长度,建议模型中可取Lp=0.08L[15].
2.2剪切变形计算
计算剪切变形采用的ASFI方法,简单来说,就是通过纤维模型分析桥墩的压弯行为,应用修正压力场理论(modifiedcompressionfieldtheory,MCFT)分析桥墩的压剪行为,并且通过力的平衡和变形协调建立压弯行为和压剪行为的关系,最终达到求解压剪弯作用下桥墩承载力和变形的目的.
ASFI方法为简化计算,将钢筋混凝土桥墩在轴力与剪力共同作用下的混凝土主压应力假设为以如图5所示的模式分布[9],即截面主压应变等于受压区混凝土矩形应力图中心处的应变,图中,σ1和σ2分别为混凝土主拉应力和主压应力,εxi,ε2i和σci分别为截面i处混凝土轴向应变,主压应变和等效压应力.

图5 ASFI方法假设的桥墩混凝土主压应力分布模式Fig.5 Concrete principal compression stress pattern of bridge columns assumed by ASFI method
假定截面i与截面i+1之间的混凝土平均主压应变[16]为

(2)
假定截面i与截面i+1之间的混凝土平均轴向应变[16]为

(3)
由平截面假定可知桥墩底部截面形心处轴向应变为

(4)
式中:h为截面高度,xn为截面受压区高度.
桥墩底部截面主压应变为

(5)
式中:β1为矩形应力等效系数[9],当混凝土抗压强度标准值fck≤22MPa时,β1取0.85,当fck>22MPa时,fck每增加5MPa,β1减小0.05[9].
因为墩顶截面弯矩为0,只有剪力和轴力,根据轴力单独作用产生的轴向应变等于轴力与剪力共同作用下轴力部分产生的轴向应变[9],可以得到墩顶截面形心处轴向应变εxin,主压应变ε2in满足

(6)
式中:ρl为纵筋配筋率,ρa为钢管含钢率,b为截面宽度,Es为钢筋弹性模量,Ea为钢管弹性模量,F为轴压力.
嵌固端与墩顶之间平均轴向应变和平均主压应变满足

(7)

(8)
由试验可知,处于压剪弯共同作用下的钢管以轴向压弯和横向受剪为主,钢管腹板沿横向(箍筋方向)的正应力可以忽略[4,17].
在箍筋屈服前混凝土平均横向应变[9]为

(9)

(10)

(11)

σcx=σx-ρlσsave-ρaσaxave.
(12)

(13)
钢筋平均应力σsave与εxave可近似认为满足理想弹塑性模型,钢管平均轴向应力σaxave与εxave也可近似认为满足理想弹塑性模型.
在箍筋屈服后混凝土平均主拉应变[9]为
ε
xave
.
(14)
式中:fsyv为箍筋屈服强度.
由摩尔应变圆知
ε1ave+ε2ave=εxave+εzave.
(15)
可以得到箍筋屈服后混凝土平均横向(箍筋方向)应变为
εzave=ε1ave+ε2ave-εxave.
(16)
σc1和σcx取值同箍筋屈服前的计算方法.
由莫尔应变圆理论知:
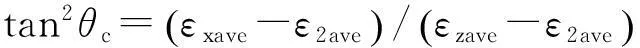
(17)
式中:θc为斜裂缝倾角.
最终得到钢筋混凝土桥墩顶部剪切位移角

(18)
由MCFT中横向变形协调条件知箍筋应变等于εzavr.在计算过程中可先按箍筋屈服前进行计算,再将εzavr与箍筋屈服应变比较可判断箍筋是否屈服.
2.3纵筋滑移变形计算

(19)


(20)
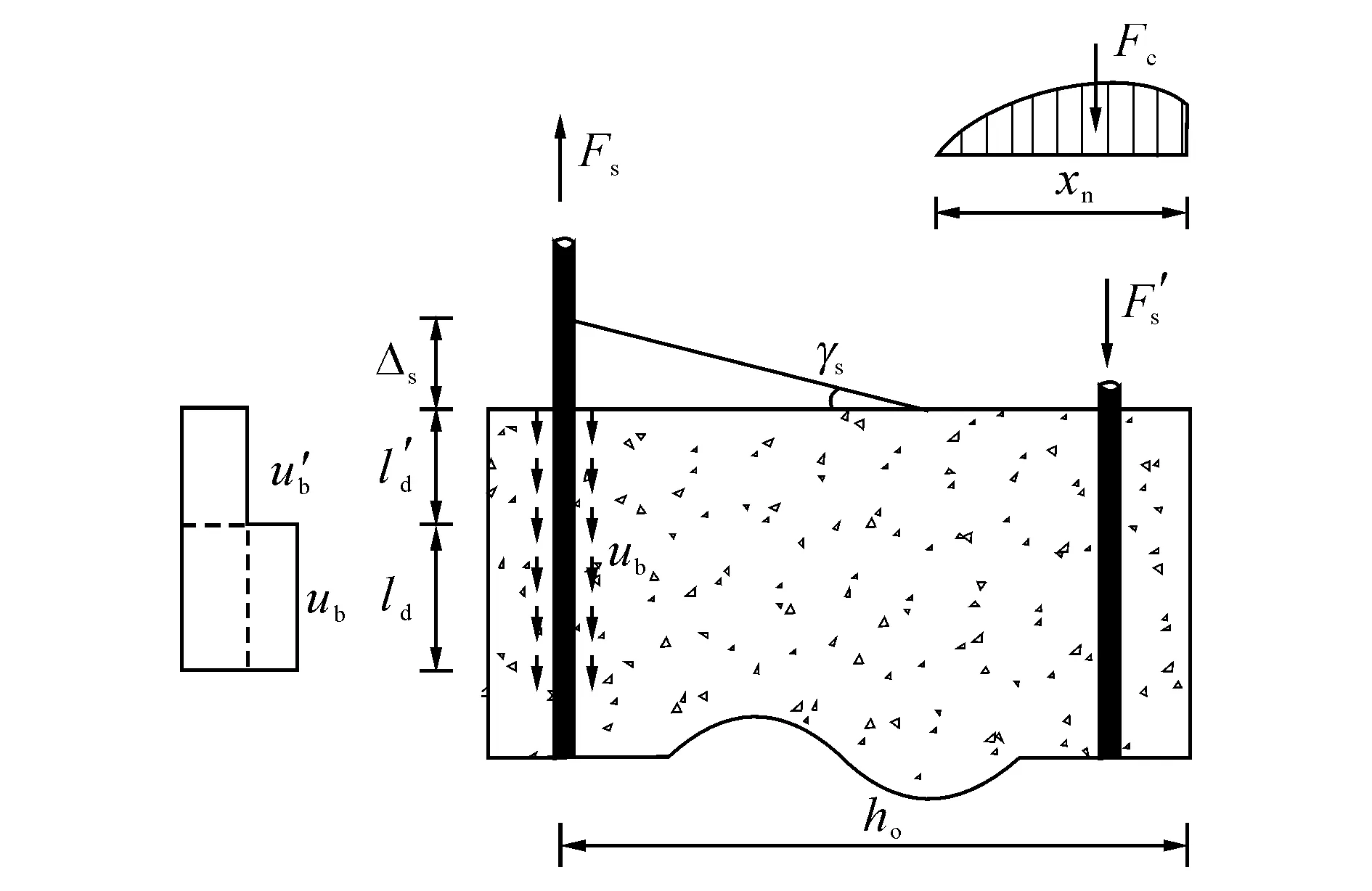
图6 桥墩底部截面处的滑移变形与受力Fig.6 Slip deformation and forces at bottom section of bridge columns
值得注意的是,当轴压比较大或桥墩延性良好时,F-Δ效应不可忽视[19]. 考虑F-Δ效应时,墩顶水平荷载FV与桥墩底部截面弯矩M满足
FV=M/L-Fγtol.
(21)
式中:墩顶总位移角γtol=γf+γv+γs.
利用建议模型计算CFSTRC桥墩变形的具体步骤如图7所示.

图7 建议模型计算流程图Fig.7 Flow chart of proposed model
3建议模型的试验验证
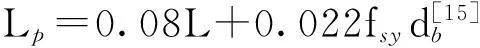

图8 建议模型结果与试验及塑性铰模型结果对比Fig.8 Results of proposed model compared with those of test and plastic hinge model
由图8可知,无论试件SS1、试件SS2还是试件SS3,建议模型的计算结果比塑性铰模型的计算结果,与试验资料吻合得更好. 塑性铰模型因为不能考虑剪切变形的影响,计算结果明显偏小.
为研究各变形组成对总变形的影响程度,给出了利用建议模型对试件SS1进行计算的细节. 如图9(a)所示,纵筋屈服前弯曲变形在总变形中的比例最高,当纵筋屈服后,弯曲变形增长速度减小,剪切变形开始快速增长,纵筋滑移变形在试件破坏前开始快速增加.如 图9(b)所示为试件SS1达到极限状态时各部分在总变形中比例,从图中可以看出剪切变形的比例最大,已经超过了总变形的一半. 已有试验研究证明,对于中等跨度的RC墩柱[20-22],剪切变形对墩柱总变形的影响较大,在剪跨比小于5时,剪切变形的贡献大于弯曲变形[22]. 因此,图9(b)的计算结果是可接受的.

图9 利用建议模型计算试件SS1各变形组成Fig.9 Calculation of various deformation components for specimen SS1 by proposed model
4结语
本文将CFSTRC桥墩的变形分为弯曲变形、剪切变形和纵筋滑移变形3个部分,以截面弯曲-曲率关系为基础,计入F-Δ效应,以塑性铰模型计算弯曲变形,以压弯剪耦合作用分析方法计算剪切变形,以Sezen和Setzler提出的纵筋滑移模型计算纵筋滑移变形,建立了能够考虑剪切和纵筋滑移影响的CFSTRC桥墩变形计算模型. 该模型满足力的平衡与变形协调条件,通过与搜集的试验数据对比,证明了该模型能够很好地计算出CFSTRC桥墩在压剪弯共同作用下的非线性变形全过程. 因此,可以利用该模型对CFSTRC桥墩的变形能力进行较准确地预测. 同时将该模型结果与塑性铰模型结果比较,发现塑性铰模型因不能考虑剪切变形,计算结果明显偏小.
参考文献(References):
[1] 卓卫东, 范立础. 延性桥墩塑性铰区最低约束箍筋用量[J]. 土木工程学报, 2002, 35(5): 47-51.
ZHUOWei-dong,FANLi-chu.Minimumquantityofconfininglateralreinforcementinthepotentialplastichingeregionsofductilebridgepiers[J]. China Civil Engineering Journal, 2002, 35(5): 47-51.
[2] PARK R, PAULAY T. Reinforced concrete structures [M]. New York: John Wiley & Sons, 1975: 221-235.
[3] 李惠, 王震宇. 钢管高强混凝土叠合柱抗震性能与受力机理的试验研究[J]. 地震工程与工程振动, 1999, 19(3): 27-33.
LI Hui, WANG Zhen-yu. Experimental research on mechanism and seismic performance of laminated column with steel tube filled with high-strength concrete [J]. Earrhquake Engineering and Engineering Vibration, 1999, 19(3): 27-33.
[4] 钱稼茹, 康洪震. 钢管高强混凝土组合柱抗震性能试验研究[J]. 建筑结构学报, 2009 (4): 85-93.
QIAN Jia-ru, KANG Hong-zhen. Experimental study on seismic behavior of high-strength concrete-filled steel tube composite columns [J]. Journal of Building Structures, 2009, 30(4): 85-93.
[5] HAN L H, LIAO F Y, TAO Z, et al. Performance of concrete filled steel tube reinforced concrete columns subjected to cyclic bending [J]. Journal of Constructional Steel Research, 2009, 65(8): 1607-1616.
[6] 廖飞宇, 韩林海. 方形钢管混凝土叠合柱的力学性能研究[J]. 工程力学, 2010, 27(4): 153-162.
LIAO Fei-yu, HAN Lin-hai. Performance of concrete-filled steel tube reinforced concrete columns with square sections[J]. Engineering Mechanics, 2010, 27(4): 153-162.
[7] JI X, KANG H, CHEN X, et al. Seismic behavior and strength capacity of steel tube‐reinforced concrete composite columns [J]. Earthquake Engineering & Structural Dynamics, 2014, 43(4): 487-505.
[8] ZHANG J, XU S Y, TANG Y. Inelastic Displacement Demand of Bridge Columns Considering Shear-Flexure Interaction [J]. Earthquake Engineering & Structural Dynamics, 2011, 40(7): 731-748.
[9] MOSTAFAEI H, VECCHIO F J, KABEYASAWA T. Deformation capacity of reinforced concrete columns [J]. ACI Structural Journal, 2009, 106(2): 187-195.
[10] MOSTAFAEI H, KABEYASAWA T. Axial-shear-flexure interaction approach for reinforced concrete columns [J]. ACI Structural Journal, 2007, 104(2): 218-226.
[11] BAI Z Z, AU F T K. Ductility of symmetrically reinforced concrete columns [J]. Magazine of Concrete Research, 2009, 61(5): 345-357.
[12] 叶列平. 混凝土结构 [M]. 2版. 北京: 清华大学出版社, 2005: 19-20.
[13] MANDER J B, PRIESTLEY M J N, PARK R. Theoretical stress-strain model for confined concrete [J]. Journal of Structural Engineering, 1988, 114(8): 1804-1826.
[14] 范立础, 卓卫东. 桥梁延性抗震设计[M]. 北京: 人民交通出版社, 2001: 152-153.
[15] 李秉南, 戴航, 张继文. 圆端形铁路桥墩变形能力分析方法研究[J]. 铁道工程学报, 2014, 31(3): 76-81.
LI Bing-nan, DAI Hang, ZHANG Ji-wen. Study on deformation capacity analysis method of round-ended railway bridge piers [J]. Journal of Railway Engineering Society, 2014, 31(3): 76-81.
[16] MOSTAFAEI H, VECCHIO F J. Uniaxial shear-flexure model for reinforced concrete elements [J]. Journal of Structural Engineering, 2008, 134(9): 1538-1547.
[17] 朱伟庆, 贾金青, 孟刚. 基于修正压力场理论的型钢超高强混凝土柱受剪承载力研究[J]. 建筑结构学报, 2013, 34(10): 101-107.ZHU Wei-qing, JIA Jin-qing, MENG Gang. Shear strength of steel reinforced high strength concrete columns based on modified compression field theory [J]. Journal of Building Structures, 2013, 34(10): 101-107.
[18] SEZEN H, SETZLER E J. Reinforcement slip in reinforced concrete columns [J]. ACI Structural Journal, 2008, 105(3): 280-289.
[19] 艾庆华, 王东升, 李宏男, 等. 基于塑性铰模型的纵筋混凝土桥墩地震损伤评价[J]. 工程力学, 2009, 26(4): 158-166.
AI Qing-hua, WANG Dong-sheng, LI Hong-nan, et al. Seismic damage evaluation of RC bridge columns based on plastic hinge model [J]. Engineering Mechanics, 2009, 26(4): 158-166.
[20] LI Y A, HUANG Y T, HWANG S J. Seismic response of reinforced concrete short columns failed in shear [J]. ACI Structural Journal, 2014, 111(4): 945-954.
[21] BRACHMANN I, BROWNING J A, MATAMOROS A. Drift-dependent confinement requirements for reinforced concrete columns under cyclic loading [J]. ACI Structural Journal, 2004, 101(5): 669-677.
[22] SEZEN H, MOEHLEoehle J P. Seismic tests of concrete columns with light transverse reinforcement [J]. ACI Structural Journal, 2006, 103(6): 842-849.
Computing model for deformation capacity of concrete filled steel tube reinforced concrete bridge columns
WANG Zhen1,WANG Jing-quan1,2,QI Jia-nan1
(1.KeyLaboratoryofConcreteandPrestressedConcreteStructureofChinaMinistryofEducation,SoutheastUniversity,Nanjing210096,China;2.NationalPrestressEngineeringResearchCenter,SoutheastUniversity,Nanjing210096,China)
Abstract:A calculation model was put forward to consider influence of shear and reinforcement slip to predict deformation capacity of concrete filled steel tube reinforced concrete (CFSTRC) bridge columns accurately. Based on the calculation results of fiber model, the model took P-Δ effect into account and divided the deformation into three components, namely flexural deformation, shear deformation and reinforcement slip deformation. The plastic hinge model was used to estimate flexure deformation, the axial-Flexure-Shear-Interaction (AFSI) method was utilized to predict shear deformation, and the reinforcement slip model was employed to calculate reinforcement slip deformation. The proposed model and plastic hinge model were utilized to predict the deformation of three test specimens provided by literatures. Results of the proposed model show good correlation with experimental values. While the plastic hinge model cannot take shear deformation into account, the results of plastic hinge model are smaller than the experimental data. Results show that shear deformation cannot be ignored when CFSTRC bridge columns are subjected to axial compression and lateral load. The proposed model can evaluate the nonlinear deformation of CFSTRC bridge columns during the whole loading process under the combination of axial load, shear and bending moment. Therefore the calculation model can be used to evaluate the deformation of CFSTRC bridge columns and gives reliable prediction.
Key words:bridge columns; concrete-filled steel tube; shear deformation; reinforcement slip; fiber model
收稿日期:2015-03-25.浙江大学学报(工学版)网址: www.journals.zju.edu.cn/eng
基金项目:国家自然科学基金资助项目(51378110);国家支撑计划资助项目(2011BAJ09B02);江苏省“六大人才高峰”第十一批资助项目(JZ-007).
作者简介:王震(1990-),男,博士生,从事桥梁延性抗震及钢组结构等研究. ORCID: 0000-0002-8776-4884. E-mail: sdkj199017@163.com通信联系人:王景全,男,副教授,博导. ORCID: 0000-0002-6637-2910. E-mail: wangjingquan@seu.edu.cn
DOI:10.3785/j.issn.1008-973X.2016.05.008
中图分类号:U 443.22; TU 392.3
文献标志码:A
文章编号:1008-973X(2016)05-0864-07

