考虑气隙变化的高速电主轴热特性仿真
李 特, 芮执元, 雷春丽, 郭俊锋, 胡赤兵
(1.兰州理工大学 数字制造技术与应用省部共建教育部重点实验室,甘肃 兰州 730050;2.兰州理工大学 机电工程学院,甘肃 兰州 730050)
考虑气隙变化的高速电主轴热特性仿真
李特1,2, 芮执元1,2, 雷春丽1,2, 郭俊锋1,2, 胡赤兵1,2
(1.兰州理工大学 数字制造技术与应用省部共建教育部重点实验室,甘肃 兰州 730050;2.兰州理工大学 机电工程学院,甘肃 兰州 730050)
摘要:为了解决电主轴高速旋转时结构变化引起的自身热特性改变的问题,提出离心膨胀和热膨胀会影响电主轴内定、转子间对流换热的观点.基于弹性力学理论,计算电主轴定、转子受离心力和热载荷而产生的径向膨胀量及由此导致的气隙变化量;根据对流换热理论得出离心力影响下泰勒数随转速和气隙长度的变化规律以及对流换热系数的变化规律.计算发现,气隙长度随定、转子的膨胀而减小,该减小量占设计值的37.7%;泰勒数随转速升高而增大,随气隙长度增大而减小;对流换热系数随气隙长度增加而降低,使得定、转子间传热受到抑制.结果表明,若能提高气隙间对流换热系数,适当提升油水冷却功率,能够大幅度降低主轴转子温升和热位移,提高加工精度.
关键词:高速电主轴,对流换热系数,气隙,温度分布,热变形
电主轴的高速旋转不仅会导致大量生热,还会引发热变形,降低加工精度甚至导致主轴失效.该问题已占主轴总变形的40%~70%,成为影响机床切削性能的主要因素之一.因此对主轴热态特性的精确建模及预测成为设计的关键.
Bossmanns等[1-4]建立了电主轴系统生热、传热、散热的功率流模型及转子-轴承的热力耦合模型,奠定了热问题的研究基础.在热问题中,生热量和传热系数的计算是建立仿真模型的关键.当前电主轴的生热与损耗问题已得到较好解决[5],但因涉及较多因素,与传热、导热有关的边界问题始终难以精确计算,如结合面热阻[6]和气隙间对流换热系数.定、转子间热量主要通过气隙传递,对流换热是影响热力学精确建模和计算的主要因素[7].Yang等[8]基于神经网络法研究了空气对流换热系数与主轴热传递的关系;Li等[9]利用RBF神经网络法计算并优化了空气对流换热系数,得到了与实验数据最接近的最优值;王保民等[10]分析了主轴的产热和散热特性,指出温度场分布的非线性特征,但认为气隙间为自然对流换热;Haitao等[11]则认为空气在气隙中的流态与流过平板时类似,与实际不符.
随着转速升高,与上述边界条件有关的参数会改变,转子的离心膨胀和热膨胀引起的主轴结构的动态变化也会导致显著的动态热传递误差[12].Chen等[13]指出在2种膨胀的综合作用下,气隙的减小会改变对流换热系数,从而改变热传递和热分布;王保民等[14]分析了这2种效应作用下主轴转子的膨胀量及气隙减小程度,发现高速时气隙减小量占设计值的很大比例;Chang等[15]监测了主轴转子的热膨胀和气隙的变化,指出主轴系统的耦合状况随膨胀量的增加变得更加复杂;Günther等[16]研究了高速转子的离心膨胀和涡动,描绘了膨胀量随转速的变化关系及对实验结果的扰动.上述文献都指出转子膨胀会造成动、热态特性的变化,但未说明这一变化对热态特性能造成何种影响,也未深入分析.
鉴此,本文基于某型号高速电主轴,从转子受离心力和热载荷产生的径向膨胀出发,讨论了定、转子间气隙的减小程度,计算了气隙对流换热系数的变化规律,分析了电主轴的热分布和热变形规律,提出了定、转子间传热效率的改善措施,旨在提高高速电主轴的传热性能与散热的控制水平,为有效的冷却和类似研究提供一定参考.
1数学模型
气隙变化量由2方面因素决定:作用于转子上的离心力和作用于定、转子上的热载荷.定子因静止只具有热膨胀,转子兼有离心膨胀和热膨胀,气隙变化量则取决于初始设计值与定、转子总膨胀量之差.
1.1气隙变化量
电主轴为轴对称结构,可等效为厚壁圆筒,为计算简便,假设定、转子材料属性相同,二者的热膨胀方程[17]可写为
平衡方程:
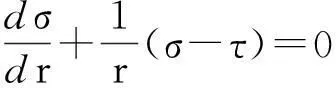
(1)
式中:σ、τ分别为径向和切向应力分量;r为转子半径.
几何方程:
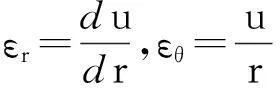
(2)
式中:εr、εθ分别为径向和切向应变分量,u为圆轴径向弹性变形.
协调方程:
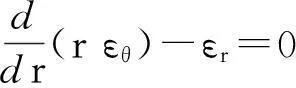
(3)
本构关系:
(4)
式中:μ为泊松比,E为弹性模量,α为材料热膨胀系数,t为转子温升.
由式(4)可得位移表达式:
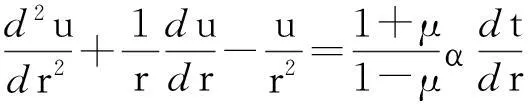
(5)
边界条件:

(6)
最终可得径向热膨胀位移表达式:
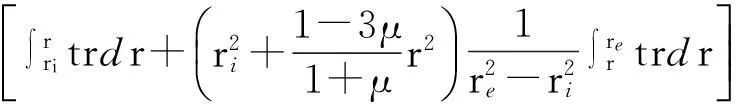
(7)
式中:re、ri分别为圆柱体的内径和外径.对式(7)取相应的积分上下限(定子内、外半径rstator.i、rstator.e或转子内、外半径rrotor.i、rrotor.e)即可分别求得定子、转子的径向热位移ust和urt.同理可得离心力作用下的转子膨胀量[16]为
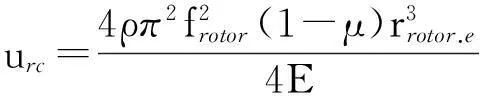
(8)
式中:ρ为材料密度,frotor为转子转频.
气隙变化量为
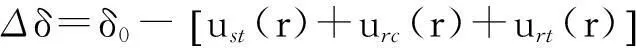
(9)
式中:δ0为初始气隙长度.
1.2主轴生热
电主轴生热主要源于电机生热、轴承生热和空气摩擦生热,前两者生热占大部分,后者占比较小.
1.2.1电机生热电机生热主要源于定子损耗和转子损耗,定子损耗又分定子铜耗和定子铁耗,转子损耗包括转子铜耗和转子铁耗,附加损耗较小可忽略,该部分生热可由电机电磁损耗关系得出[1,5].通常认为定子发热量占功率损耗的2/3,转子发热量占功率损耗的1/3[10].本文电机损耗为3 kW,可知定子和转子的损耗分别为2和1 kW.
1.2.2轴承生热[10]角接触球轴承的生热主要源于滚珠与内、外圈及润滑液的摩擦,其发热量可由下列算式得出
PQ=1.047×10-4n M.
(10)
式中:PQ为轴承生热量,n为轴承内圈转速,M为总摩擦力矩,其由2项构成:M1为与所受载荷有关的摩擦力矩,M2为与润滑液黏度有关的力矩.三者关系为
M=M1+M2.
(11)
其中:
M1=f1p1dm.
(12)
(13)
式中:f1为与轴承载荷和结构有关的系数,当角接触球轴承时f1=0.001[10];p1为轴承当量载荷;dm为轴承节圆直径;f0为与轴承类型和润滑有关的参数,当油气润滑时f0=1[10];ν0为润滑油运动黏度.各轴承发热量随转速n的关系如图1所示,前轴承定位预紧,后轴承定压预紧,预紧力为100 N.
因前轴承尺寸较大,定位预紧时在热诱导预紧力作用下生热大于后轴承,该差距随转速升高进一步增大,同时生热也随润滑液黏度的升高而增加.

图1 轴承发热量与转速关系Fig.1 Relationship between heat and speed
1.2.3风阻损耗因主轴转速很高,定、转子间的空气摩擦损耗较为严重,风阻损耗[2]可表示为

(14)
式中:lr为转子长度;ηair为空气动力黏度,取为18.5×10-6Pa·s2.该式中气隙长度被视为恒值,本文因考虑了气隙长度的变化,即Δδ.
2边界条件
主轴传热分为热传导、热对流和热辐射,热辐射因数值较小可忽略,热传导与结合部接触状态有关,热对流则取决于间隙中空气的流态.
2.1结合面接触热阻
主轴内存在大量结合部,主要包括球与轴承内、外套圈,轴承外圈与轴室,轴承内圈与主轴转子,主轴转子与电机转子等.轴承内的热传递通过球与滚道的导热和润滑油气的对流进行.各结合面间的传热系数可由下列关系式确定:
2.1.1球与轴承内、外圈热阻[10,18]为

(15)
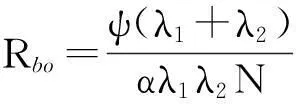
(16)
式中:Rbi、Rbo分别为球与内圈和外圈滚道的接触热阻,λ1、λ2与λ3分别为外圈、球和内圈材料的导热系数,N为滚珠数目,ψ为与接触面积大小有关的几何因子,它是k=1-(b2/a2)的函数:

(17)

(18)
式中: θ为滚珠位置角;GI为球与轴承内外面的热导;R为球与滚道间的接触热阻;A为球与滚道的Hertz接触面积;a、b分别为椭圆接触面的半长轴和半短轴;可见Rbo、Rbi与预紧力有关,预紧力越大热阻越小[19].计算可得前轴承内外圈热导率:Gi=0.205W/K,Go=0.21W/K;后轴承内外圈热导率:Gi=0.172W/K,Go=0.179W/K.
2.1.2轴承外圈与轴室热导[18]为

(19)
式中:sr、sg分别为外圈厚度和周向气隙厚度;λa为空气导热系数,λa=0.026(W/m·K).由于热膨胀,外圈与轴室的间隙不再是常量[1,19]:
sg=s0-[(tr-t0)αr-(th-t0)αh]rrotor.i.
(20)
式中: s0为初始气隙厚度,tr轴承外圈温度,t0为初始环境温度,th为轴室温度,th=60 °C,tr=64 °C,t0=22 °C.热膨胀系数为[19-20]α=2.3×105K-1,计算可得前轴承热导GII=3.6W/K,后轴承GII=3.12W/K.
2.1.3其他结合部轴承内圈与主轴、电机与主轴之间通常采用过盈配合,接触热阻可表示[6]为
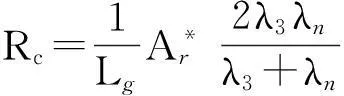
(21)
2.2对流换热系数
对流换热分为强迫对流换热和自由对流换热,在电主轴中,强迫对流换热包括轴承与润滑油气,定子与冷却水套,定、转子与气隙间的热交换等;自由对流换热包括转子端部、主轴壳体与周围空气间的热交换等.对流换热系数为

(22)
式中:Nu 为努赛尔数,λ为介质导热系数,Dh为等效尺寸.
2.2.1定转子气隙内的对流换热系数轴承油气润滑系统的气流会使定子和转子温升轻微下降,但因距离较远,影响程度较为微弱,因此认为定、转子气隙中无轴向气流[10].转子在静止的定子中旋转时,气隙内空气流态为泰勒库特流,它会大幅改变两者间的传热特性,当转子转速大于临界转速时,空气将会失稳,并产生二次流.因此对气隙内的对流换热问题首先需判断流态,继而选取适当的计算方程.通常采用泰勒数(Ta=41.19)判断流态[21],但以临界转速判断更为直观.当气隙长度远小于气隙圆环平均半径时,临界转速为

(23)
式中:rm为气隙圆环平均半径,ν为空气的运动黏度.
如图2所示为当气隙δ0=0.3 mm时,泰勒数Ta随电机转子外表面直径d1和转速n的变化关系.由图2可得:泰勒数随转子直径和转速的上升而增大,在同一转速下,转子直径越大,泰勒数上升越快;若直径不变,转速是决定流态的主要因素.当泰勒数大于临界值41.19时,空气将失稳而产生泰勒涡.由图2可知,当转速大于15 000 r/min时,不论转子直径如何,气隙内空气都将失稳.本文电主轴转子直径为82 mm,从图2中可知只要转速大于7 500 r/min,空气定会失稳,且转速越大失稳越严重.当计及转子的径向膨胀时,该失稳则有进一步增强之势.
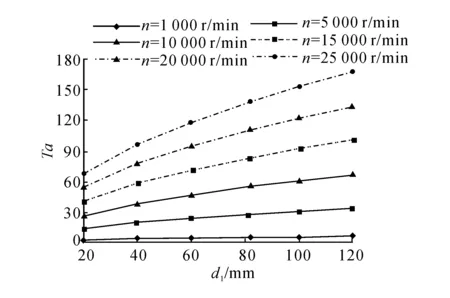
图2 泰勒数随转子直径和转速的变化曲线Fig.2 Change rule of Taylor number with rotor diameter and rotational speed variation
当高速时,气隙内空气皆为紊流,努赛尔数为
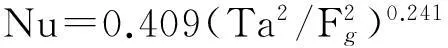
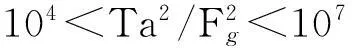
(24)
式中:
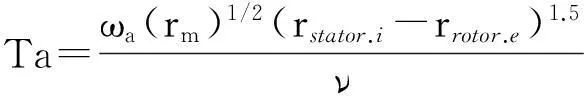
(25)
Fg与S皆为几何因子.

(26)
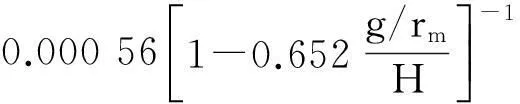
(27)
式中:rm=(rsotor.e+rstator.i)/2; H=1-(rtator.i-rrotor.e/2rm),ωa为主轴角速度,g为重力加速度.
2.2.2其他对流换热系数其他努赛尔数Nu及对流换热系数h见表1.表中Pr为普朗特数,当介质为空气时Pr取0.707,为水时Pr取0.583;Dh=2(rstaor.i-rrotor.e);Re为雷诺数,Re=v rrotor.e/ν,v为空气流速,l为传热面几何特征长度.
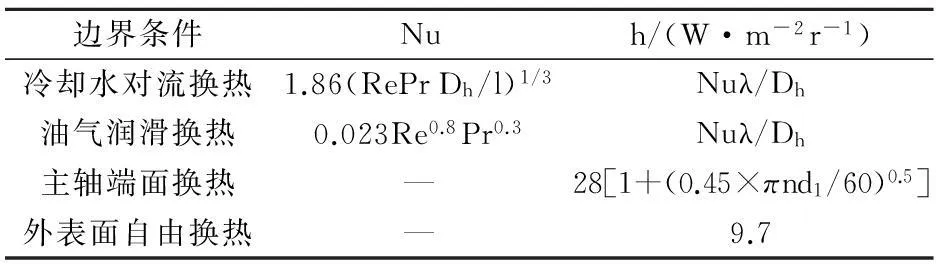
表1 其他对流换热系数计算
3建模与仿真
电主轴主要参数如表2所示,建立的三维模型如图3所示.因电主轴为轴对称,因此只需建立1/4模型,同时忽略螺纹孔,倒角等影响不大的几何因素,并将冷却水槽等效为环形槽.精确划分网格后有162 094个单元,290 652个节点,仿真设环境温度为22 °C.

表2 电主轴主要结构参数

图3 电主轴三维模型Fig.3 3D model of high speed spindle
3.1主轴膨胀与气隙变化
3.1.1主轴离心膨胀、热膨胀及气隙减小量根据1.1的分析,离心力和热载荷都将引起主轴膨胀,为准确计算该变形,将离心膨胀与热膨胀单独计算.将主轴模型导入Ansys Workbench软件中,施加绕轴转速即可得到相应的离心膨胀位移,如图4所示.从图4可见,该膨胀量随转速上升而增大,当转速最大时,膨胀量达到最大值.

图4 转子径向膨胀量随转速变化曲线Fig.4 Rotor expansion curve under rotation speed effect
与离心膨胀不同,在热载荷作用下主轴转子与壳体都会产生热膨胀.当主轴旋转时,生热与热传递、对流换热及散热等都为动态变化过程,所导致的热膨胀难以测量,由图4分析可知,当转速最大时离心膨胀达到最大值,为简便起见,计算20 000 r/min时所对应的热膨胀量.此时转子内、外表面温度分别为118和113 °C,转子轴内表面温度为115 °C,定子内外表面温度分别为70 和35 °C[14],由此可得壳体内表面和转子外表面的热膨胀量分别为25.2和82.2 μm,总膨胀量为107.4 μm,而该转速时离心膨胀量为5.7 μm,因此气隙减小量为113.1 μm,可见气隙减小程度主要取决于壳体和转子的热膨胀.只有在离心力作用时,气隙变化量占总宽度的3.25%;只有在热载荷时,气隙变化量占总宽度的35.8%;在综合作用下气隙减小量占初始宽度的37.7%;因此精确计算时该变化不可忽略.同时可预测:对于高DmN值高功率电主轴,高转速下发热和离心力引起的综合膨胀更大,气隙将急剧减小,若膨胀量进一步增大,将会引起转子摩擦定子,导致电主轴损坏.
3.1.2气隙减小对风阻损耗的影响如图5所示为不同条件下空气摩擦损耗的变化,从图5中可见摩擦损耗随转速升高而增大,在同一转速下当考虑气隙变化时,摩擦损耗更大.以n=20 000 r/min时为例,不考虑膨胀时风阻损耗为21.08 W,只考虑离心膨胀时为21.48 W,只考虑热膨胀时为32.97 W,考虑综合膨胀时为33.49 W,与不考虑膨胀时相比,损耗增加了58.87%,这说明气隙变化对风阻损耗有重要影响,而热膨胀影响最大.一方面是因为该损耗与转子直径的三次方成正比,与气隙长度成反比;另一方面由于气隙的减小,速度梯度减小,空气流动更加不稳定,空气剪切力增大,做功增大,摩擦加剧,从而使得损耗增大.
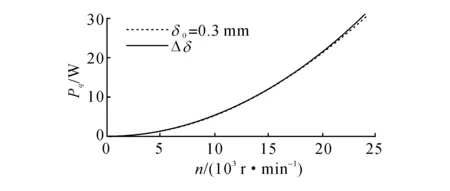
图5 气隙对风阻损耗的影响Fig.5 Influence of air gap on windage loss
3.1.3泰勒数与对流换热系数如图6所示为泰勒数变化规律,Ta随转速升高而增大,当转速大于7 500 r/min时即会导致空气失稳,从而产生二次流.同时可看到,考虑气隙变化时泰勒数呈下降趋势,当n=20 000 r/min时,若只考虑离心膨胀,泰勒数为107.54,只考虑热膨胀时泰勒数为56.95,考虑综合膨胀时则为54.44,泰勒数分别下降了2.8%,48.5%,50.8%.可见热膨胀导致的气隙减小对泰勒数的大小有决定性影响.

图6 泰勒数随转速变化曲线Fig.6 Curve of taylor number versue rotation speed

图7 对流换热系数随气隙长度的变化曲线Fig.7 Convective heat transfer coefficient versus air gap variation
如图7所示为对流换热系数的变化规律,从图7可见ha随转速升高而增大.在同一转速下,考虑气隙减小时对流换热系数轻微减小,但与转速的作用相比,该变化的影响可以忽略不计.当n=20 000 r/min,不考虑气隙变化、只考虑离心力、只考虑热载荷及考虑综合因素时对流换热系数分别为202.14、201.76、193.63、193.10 W/(m2·K),可见对流换热系数随气隙减小而减小.该减小比例依次为0.18%,4.21%,9.04%,因此热膨胀导致的气隙减小对对流换热系数有重要影响,并可能对温度分布造成一定影响.
3.2主轴系统热分布
3.2.1定、转子间的热分布边界条件对热分布的结果有较大影响,如8、9所示为考虑与未考虑结合面热阻时的热分布图,考虑热阻后各结合部温度梯度增大,以主轴转子和电机转子结合部的变化最为明显.电机转子温度由112.8 °C上升为114.84 °C,上升了1.8%;主轴转子外表面温度则由112.8 °C下降至107.57 °C,下降了5.23%.主轴转子和电机转子间温度梯度由6.59 °C增大至7.27 °C,增长了10.3%,说明在热阻作用下,电机转子产生的热量不能顺利传入主轴转子.观察轴承内、外套圈分别与主轴转子和壳体的结合面,也可得出同样的结论,即当考虑结合面热阻后,轴承滚珠、内圈和外圈处的温度均出现热集中,温度值有所上升.这说明在电主轴热分析时不能忽略结合面热阻,否则将引起较大误差.
如图10所示为考虑气隙变化时的热分布,与图9相比可知,转子温度幅值有较大变化,每个温度梯度所对应的温度值有所上升.如电机转子表面最高温度较之前升高3.34 °C,主轴转子外表面温度则上升了2.58 °C.这也印证了前面的分析,即气隙减小一方面增加了空气摩擦损耗,增加的损耗以生热的形式作用于转子表面,使其温度上升;另一方面降低了对流换热系数,使转子与定子间的对流换热受阻,转子上的热量难以交换至定子上的水冷系统.两者综合作用的结果使主轴温升增加,这也与文献[22]的实验结果一致,进一步说明了分析的正确性.
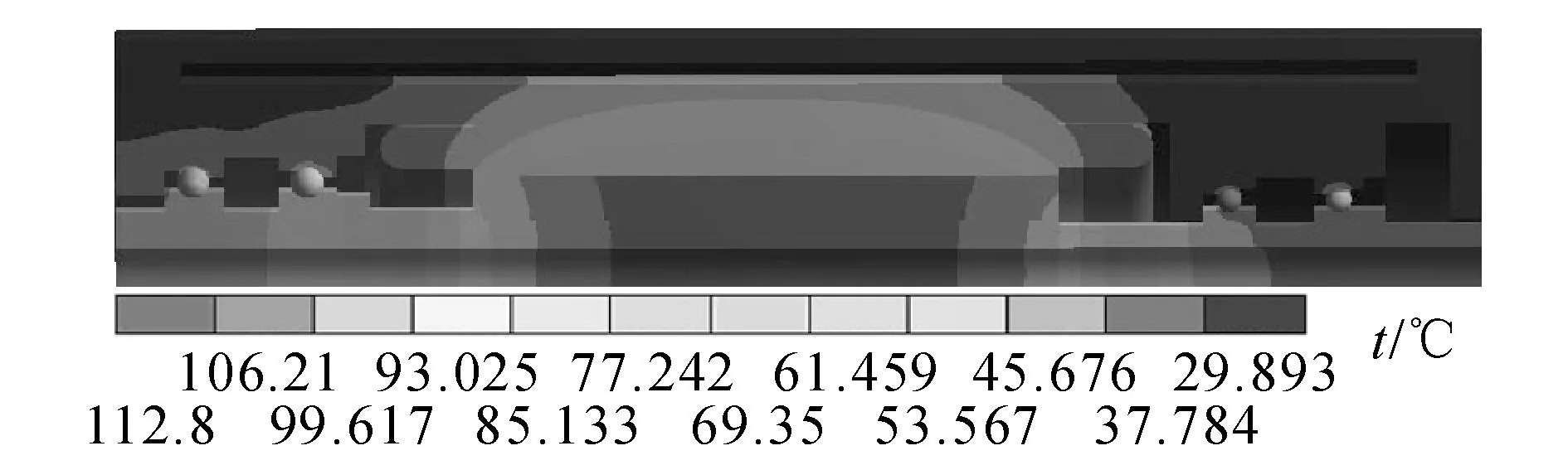
图8 未考虑结合面热阻的热分布Fig.8 Thermal distribution without thermal resistance effect
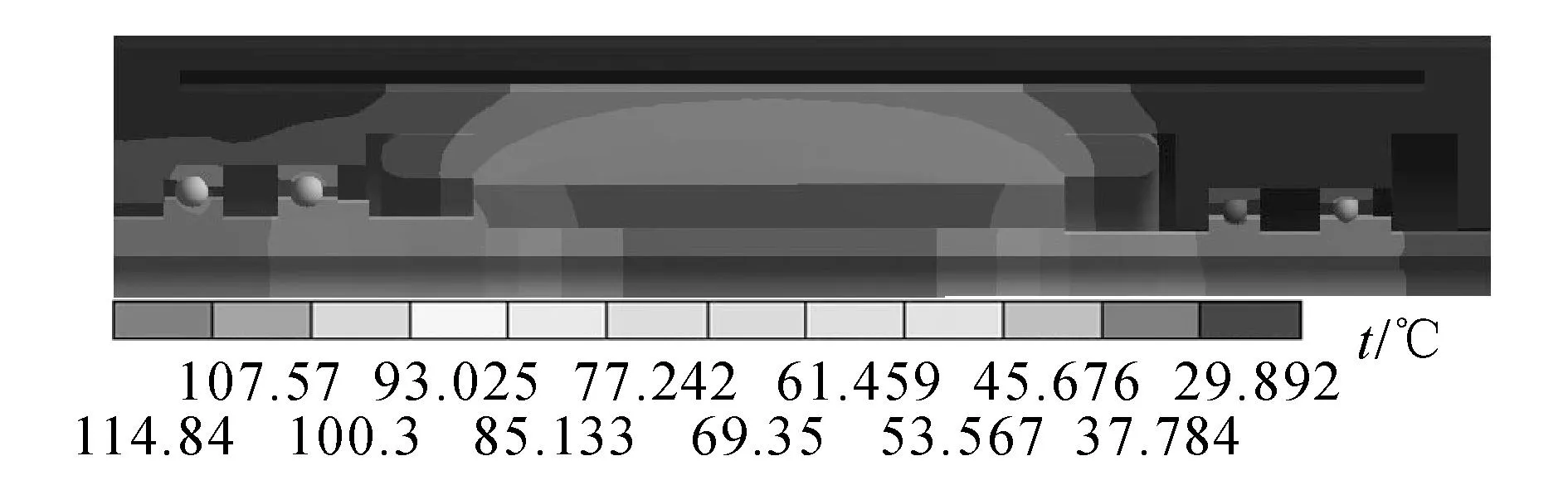
图9 考虑结合面热阻的热分布Fig.9 Thermal distribution under thermal resistance effect
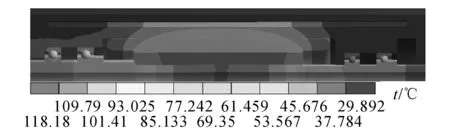
图10 考虑气隙变化时的热分布Fig.10 Thermal distribution considering air-gap variation
3.2.2转子温升与轴向热变形轴向变形能严重影响电主轴的加工精度,而径向变形对此类主轴影响不大,因此只考虑转子的轴向热变形.为进一步明确转子温度及热变形与对流换热系数和冷却功率之间的关系,绘制如图11、12曲线图.如图13所示为电机转子表面温度与对流换热系数关系,图中Pc为冷却水功率,t为电机转子表面温度,ha为气隙对流换热系数,由图11可知:电机转子温度随对流换热系数的增加而减小,对流换热系数每减小10 W/m2k,温度平均降低2.6 °C.如图12所示为轴向热变形量随对流换热系数的变化规律,图中δrotor.x为主轴轴向热变形量.从图12中可知δrotor.x随ha的增加显著下降,对流换热系数每减小10 W/m2k,热变形量平均下降2.47 μm.如图13所示为不同冷却功率下转子温度变化速率Δt与对流换热系数变化量Δha之间的关系,由图13可知温度并非等比例降低,降低速率Δt非线性变缓.如图14所示为主轴轴向位移变化速率Δδrotor.x与对流换热系数变化量Δha之间的关系,从图14中可知Δδrotor.x随Δha的上升而下降.从图13、14看出:若对流换热系数不变,提高冷却水功率并不能明显降低转子温度,这说明对流换热系数存在一个最优区间,否则若一味的提高该系数,将会造成过高的成本浪费.

图11 电机转子表面温度与对流换热系数关系Fig.11 Relationship between rotor surface temperature and convection heat transfer coefficient

图12 主轴轴向变形与对流换热系数关系Fig.12 Relationship between rotor axial displacement and convection heat transfer coefficient

图13 转子温度变化速率Fig.13 Change rate of rotor temperature
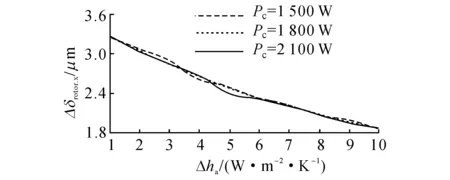
图14 轴向位移变化速率Fig.14 Change rate of axial displacement
温度分布的变化规律进一步说明:定、转子间的热传递主要靠气隙间空气的对流换热,因此如何提高对流换热系数则成为解决该问题的关键,若能提高,则转子温度会大幅度降低.可以效仿中大型电机进行轴向强制风冷,但目前该技术在电主轴中应用较为困难.若能风冷的基础上,一方面提高水冷效率,或者对转子单独进行水冷,则能从根本上改善电主轴转子的热变形特性.
4结论
(1)离心膨胀和热膨胀都会使得气隙长度显著减小,热膨胀的影响远大于离心膨胀;中小型电主轴的气隙长度较小,气隙变化明显,若其减小程度过大则会导致转子摩擦定子,损坏电主轴.
(2)空气摩擦损耗随气隙减小而上升;对流换热系数随转速上升而增大,在同一转速下,该系数随气隙的减小而减小,影响程度不能忽略;其中离心膨胀的影响较小可忽略,但热膨胀对该系数的变化幅度有决定性影响,因此进行精确热分析时必须考虑该因素.本文未考虑齿槽形状、数目及转子表面粗糙度等因素,上述因素能否显著影响定转子间的对流换热还需更进一步研究.
(3)建模时必须考虑结合部热阻,否则会使仿真结果产生较大误差.
(4)提高冷却水功率并不能有效降低转子温升,而提高气隙间对流换热系数则会显著降低转子表面温度、温度梯度及转子轴向热变形量,此时若提高冷却功率,则能显著改善转子轴向热变形特性.
参考文献(References):
[1] BOSSMANNS B, TU J F. A thermal model for high speed motorized spindles[J]. International Journal of Machine Tools and Manufacture, 1999, 39(9): 1345-1366.
[2] BOSSMANNS B, TU J F. A power flow model for high speed motorized spindles—heat generation characterization [J]. Journal of Manufacturing Science and Engineering, 2001, 123(3): 494-505.
[3] JORGENSEN B R, SHIN Y C. Dynamics of machine tool spindle/bearing systems under thermal growth[J]. Journal of Tribology, 1997, 119(4): 875-882.
[4] LI H, SHIN Y C. Integrated dynamic thermo-mechanical modeling of high speed spindles, part 1: model development[J]. Journal of Manufacturing Science and Engineering, 2004, 126(1): 148-158.
[5] 陈小安,张朋,合烨,等. 高速电主轴功率流模型与热态特性研究[J]. 农业机械学报,2013,44(9):250-254.
CHEN Xiao-an, ZHANG Peng, HE Ye, et al. Power flow model of high speed motorized spindles and its thermal characteristics [J]. Transactions of the Chinese Society for Agricultural Machinery, 2013,(44)09:250-254.
[6] MIN X, SHUYUN J, YING C. An improved thermal model for machine tool bearings[J]. International Journal of Machine Tools and Manufacture, 2007, 47(1): 53-62.
[7] HOWEY D A, CHILDS P R N, Holmes A S. Air-gap convection in rotating electrical machines[J]. IEEE Transactions on Industrial Electronics, 2012, 59(3): 1367-1375.
[8] YANG Z, SUN M, LI W, et al. Modified Elman network for thermal deformation compensation modeling in machine tools[J]. The International Journal of Advanced Manufacturing Technology, 2011, 54(5/8): 669-676.
[9] LI D, FENG P, ZHANG J, et al. Calculation method of convective heat transfer coefficients for thermal simulation of a spindle system based on RBF neural network[J]. The International Journal of Advanced Manufacturing Technology, 2014, 70(5/8): 1445-1454.
[10] 王保民,胡赤兵,孙建仁,等. 高速电主轴热态特性的ANSYS仿真分析[J]. 兰州理工大学报,2009,(35)1:28-31.
WANG Bao-min, HU Chi-bing, SUN Jian-ren, et al, Simulation analysis of thermal characteristics of high-speed motorized spindle by using ANSYS[J]. Journal of Lanzhou university of technology, 2009,35(1):28-31.
[11] HAITAO Z, JIANGUO Y, JINHUA S. Simulation of thermal behavior of a CNC machine tool spindle[J]. International Journal of Machine Tools and Manufacture, 2007, 47(6): 1003-1010.
[12] ABELE E, ALTINTAS Y, BRECHER C. Machine tool spindle units[J]. CIRP Annals-Manufacturing Technology, 2010, 59(2): 781-802.
[13] CHEN J S, HSU W Y. Characterizations and models for the thermal growth of a motorized high speed spindle[J]. International Journal of Machine Tools and Manufacture, 2003, 43(11): 1163-1170.
[14] 王保民, 胡赤兵, 邬再新, 等. 高速电主轴定转子的气隙变化及影响因素[J]. 兰州理工大学学报, 2009, 34(6): 40-42.WANG Bao-min, HU Chi-bing, WU Zai-xin, et al. Analysis of variation in air-gap between rotor and stator in high-speed motorized spindle [J]. Journal of Lanzhou university of technology, 2009, 34(6): 40-42.
[15] Chang C F, Chen J J. Vibration monitoring of motorized spindles using spectral analysis techniques[J]. Mechatronics, 2009, 19(5): 726-734.
[16] GNTHER P, DREIER F, PFISTER T, et al. Measurement of radial expansion and tumbling motion of a high-speed rotor using an optical sensor system[J]. Mechanical Systems and Signal Processing, 2011, 25(1): 319-330.
[17] 徐秉业,刘信声.应用弹塑性力学[M].北京,清华大学出版社,1995:203-205,237-241.
[18] NAKAJIMA K. Thermal contact resistance between balls and rings of a bearing under axial, radial, and combined loads [J]. Journal of thermophysics and heat transfer, 1995, 9(1): 88-95.
[19] JIANG S, MAO H. Investigation of variable optimum preload for a machine tool spindle[J]. International Journal of Machine Tools and Manufacture, 2010, 50(1): 19-28.
[20] 王保民. 电主轴热态特性对轴承—转子系统动力学特性的影响研究[D].兰州:兰州理工大学,2009.
WANG Bao-min. Study on thermal characteristics of high-speed motorized spindle and its effects on dynamic characteristics of ball bearing-rotor system[D]. Lanzhou: Lanzhou university of technology, 2009:18-33.
[21] STATON D A, CAVAGNINO A. Convection heat transfer and flow calculations suitable for electric machines thermal models[J]. IEEE Transactions on Industrial Electronics, 2008, 55(10): 3509-3516.
[22] 张丽秀. 电主轴单元电磁特性及控制策略改善研究[D].大连:大连理工大学,2012:88-90.
ZHANG Li-xiu, Research on improvement of electromagnetic properties and control strategy of motorized spindle Cells[D].Dalian: Dalian university of technology, 2012:88-90.
Simulation of thermal characteristics of high speed spindle considering air gap variation
LI Te1,2,Rui Zhi-yuan1,2,LEI Chun-li1,2,GUO Jun-feng1,2,HU Chi-bing1,2
(1.KeyLaboratoryofDigitalManufacturingTechnologyandApplication,TheMinistryofEducation.LanzhouUniversityofTechnolagy,Lanzhou730050,China;2.CollegeofMechano-ElectronicEngineering,LanzhouUniversityofTechnology,Lanzhou730050,China)
Abstract:A viewpoint on the centrifugal expansion and thermal expansion which would affect the convection heat transfer between stator and rotor of high speed spindle was proposed to solve the problem that the thermal characteristics caused by structure variation of high speed spindle would be changed under high rotation speed. Based on the theory of elastic mechanics, radical expansion and air gap changes which caused by the radical expansion were calculated considering the two expansions acting on the stator and rotor of spindle. Variation rules of air gap and convection heat transfer coefficient that affected by the centrifugal force were obtained according to the convection heat transfer theory. The calculation results show that the air gap length decreases with the expansion of the rotor, and the reduction is 37.7% of the design value. The Taylor number increases with the increase of the rotating speed, while decreases with the increase of the air gap length. The heat transfer coefficient of air gap decreases with the increase of air gap length, so that the heat transfer between the stator and rotor is restrained. Results show that the temperature rises and thermal displacement can be significantly reduced if the convection heat transfer coefficient and the cooling power can be properly promoted, then the machining accuracy can be improved.
Key words:high speed spindle; convection heat transfer coefficient; air gap; temperature distribution; thermal deformation
收稿日期:2015-05-04.浙江大学学报(工学版)网址: www.journals.zju.edu.cn/eng
基金项目:国家自然科学基金资助项目(51465035,51465034);国家重大数控专项资助项目(2010 ZX04001-032);甘肃省青年科技基金计划资助项目(145RJYA307).
作者简介:李特(1987-),男,博士生,从事高速电主轴动态性能等研究.ORCID: 0000-0001-9734-0404. Email:lite126126@126.com通信联系人:芮执元,男,教授. ORCID: 0000-0003-2251-8014. Email:zhiy_rui@163.com.
DOI:10.3785/j.issn.1008-973X.2016.05.018
中图分类号:TH 122; TH 133
文献标志码:A
文章编号:1008-973X(2016)05-0941-08

