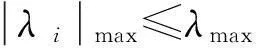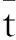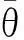基于tau矢量场制导的多无人机协同standoff跟踪方法

杨祖强,方　舟,李　平,2

(1.浙江大学 航空航天学院,浙江 杭州 310027; 2. 浙江大学 控制科学与工程学院,浙江 杭州 310027)



基于tau矢量场制导的多无人机协同standoff跟踪方法

杨祖强1,方舟1,李平1,2

(1.浙江大学 航空航天学院,浙江 杭州 310027; 2. 浙江大学 控制科学与工程学院,浙江 杭州 310027)

摘要:针对有时间约束的多无人机(UAV)协同standoff跟踪需求,研究基于四维矢量场的多UAV协同制导方法.利用本征tau-G制导策略能够依照期望时间对各运动状态进行同步规划的特性,构建tau制导矢量场,并在此基础上提出综合性多UAV协同standoff跟踪方法.该方法用tau矢量场导引各UAV的位置在期望时间准确收敛于目标圆,利用tau-G策略调整UAV之间的相位间隔,应用序列二次规划对跟踪参数进行优化,并采用人工势场法进行协同避碰避障.仿真结果表明,基于tau矢量场制导的协同standoff跟踪方法计算负荷低,跟踪偏差小、制导策略可飞性好,飞行安全性高,能够更好地满足多UAV协同standoff跟踪的应用需求.

关键词：广义tau理论；tau矢量场制导；standoff跟踪；多机协同

多无人机(unmanned aerial vehicle,UAV)协同standoff跟踪[1]是一类基本的多机协同任务.在该任务中,多架UAV以目标为圆心,按照一定相位间隔环绕目标做圆周运动.期望的圆周轨迹被称为目标圆,圆周半径为standoff距离.多UAV协同standoff跟踪既可保证机载传感器对目标有效覆盖,又能降低任务风险,因而在目标定位、交通管制等领域有广阔的应用前景.

目前已有的standoff跟踪方法包括“优秀舵手”法[2],路径塑造[3],非线性模型预测控制[4],参考点制导[5],矢量场制导等.矢量场制导在standoff跟踪问题中应用最广,主要包括Lyapunov矢量场制导(lyapunov vector field guidance,LVFG)[1, 6]、Tangent矢量场制导 (tangent field guidance,TVFG)[7]、T+LVFG[8]等.然而,已有的矢量场制导方法通常导引UAV在时间t→∞时渐进收敛于目标圆,而在协同standoff跟踪中则期望各UAV能够在期望时间按照相位间隔收敛.同时,已有方法在跟踪制导时通常先用矢量场将UAV导引至目标圆,再调整相位间隔,放弃了收敛过程中的相位调整机会,延长了跟踪形成的时间.最后,目前缺乏包含参数优化、矢量场制导、相位调整和避障等功能的综合性协同standoff跟踪方法.

为弥补已有矢量场制导方法的缺陷,应将时间信息融入矢量场中进行四维制导.近年来,生物启发的tau理论在四维运动规划领域日益受到关注[9].Tau理论在塘鹅捕鱼[10],鸽子着陆[11]等动物运动规划的研究基础上提出,该理论认为视觉线索tau(τ)提供了在动物运动规划中具有重要作用的接触时间[12].Lee[13]将tau广义化为运动物体由当前运动状态转换到目标状态所需的接触时间,提出了广义tau理论,使tau可用于任何有目标的运动制导.应用广义tau理论的仿生知识,研究者提出了本征tau-G制导策略(Intrinsic tau-G guidance strategy,tau-G策略)[13].该策略可严格依照时间约束对位置、速度、加速度进行同步规划,并可保证运动状态的平稳过渡[14]；同时,tau-G策略形式简单,易于优化；因而在四维制导任务中优势显著.目前tau-G策略已被应用于UAV的运动规划中,如刹车与着陆[15],鸟类停驻的模拟[16]等.

为克服已有方法的缺陷,本文利用tau-G策略构建tau矢量场,该矢量场可按照期望时间将各UAV导引至目标圆,实现制导维度的扩展.基于tau矢量场制导(tau vector field guidance,τVFG),本文提出了一种多机协同standoff跟踪方法.该方法利用τVFG生成UAV的制导速度；在位置收敛过程中,同步采用tau-G策略规划纵向飞行速度以调整UAV的相位间隔；并利用人工势场法实现各UAV与障碍之间的避碰.

1多机协同standoff跟踪问题

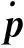
图1　3架UAV协同standoff跟踪示例Fig.1　Cooperative standoff tracking by three UAVs

为了保证对目标的持续standoff跟踪,本文将跟踪过程分为2段：在期望时间td内导引各UAV位置收敛于目标圆并调整相位至期望间隔的阶段为跟踪形成段；当跟踪形成后,保持对目标的持续standoff跟踪为跟踪保持段.

在导航坐标系下,UAV的运动学模型为

(1)

式中:U=[ux,uy,uz]为UAV的3轴空速矢量,即矢量场为UAV提供的制导策略,W=[wx,wy,wz]为风速,ψ为UAV的航迹角.

制导策略需满足的约束条件为

(2)

式中:vamax和vamin分别为最大和最小空速,ωmax为最大转弯角速率,λmax为最大爬升/下滑率,最小转弯半径约束Rmin=vamin/ωmax已包含于式(2)中.

2tau制导矢量场的构建

2.1本征tau-G制导策略

在广义tau理论中,tau变量定义为

(3)

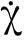
Tau-G策略基于广义tau理论提出,已有生物学研究表明,该策略在人和动物的运动平衡控制[17]、音乐演奏[18]等行为的规划中发挥制导作用.Tau-G策略的内容为：若真实运动间距χ与虚拟的本征制导运动G(t)的tau变量在闭合过程中保持非零常数比率kχ,则2种运动的间距将在到达时间T同时闭合.kχ被称为耦合系数,G(t)为重力作用下的自由落体运动,其与τG(t)的表达式为

(4)

(5)

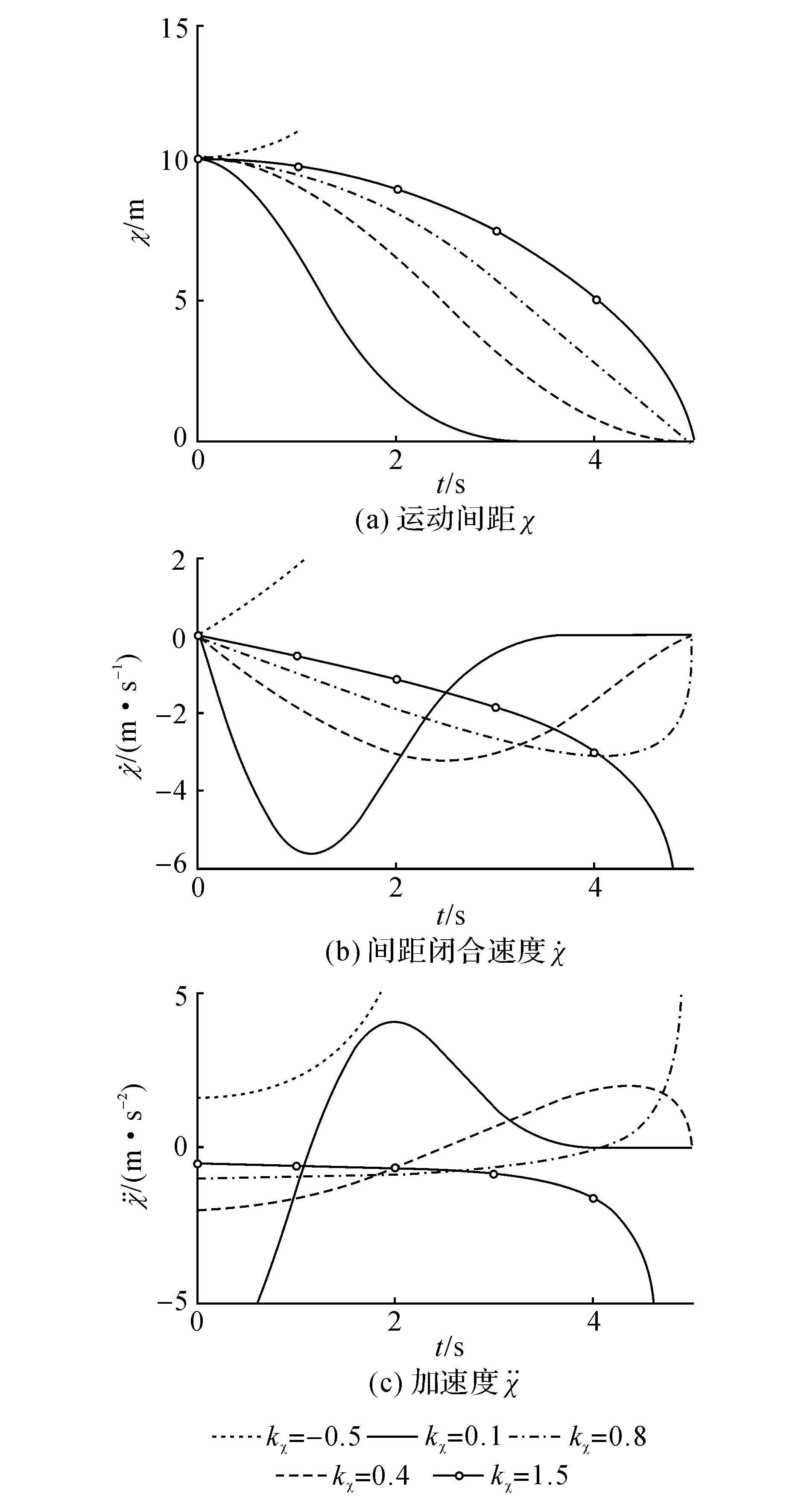
图2　kχ的不同取值对tau-G策略制导的影响Fig.2　Tau-G guidance with different k values

2.2tau制导矢量场

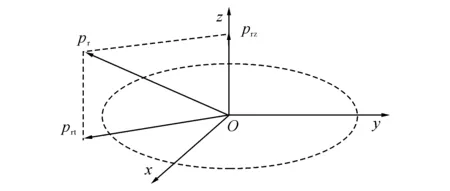
图3　相对坐标矢量的分解Fig.3　Decomposition of relative position vector

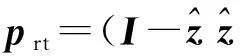
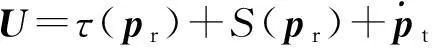
(6)

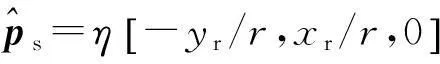
(7)

式(7)仅根据UAV的初始位置进行制导,但由于UAV的避障动作、速度控制误差和风扰等因素的影响,prt、prz不会严格按照式(7)收缩,甚至会严重偏离期望收敛过程.此时若不根据实际位置和当前时刻对r0、Δh0进行修正,则难以保证UAV的位置在td时刻收敛于目标圆.为保证矢量场能够为各时刻、各位置的UAV提供合适的制导矢量,在时刻t需根据实际位置求得r0和Δh0为

(8)

将式(7)、(8)代入收缩项τ(pr)可得

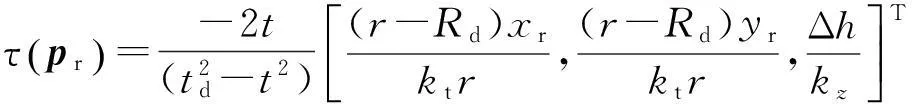
(9)

设vs=‖S(pr)‖,为使UAV尽量按照应飞速度运行,即‖U‖=vd,则vs应满足方程：

(10)

(11)

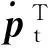
1) 在不超过vamax的情况下增大应飞速度vd；

2) 调整τVFG的耦合系数集[kt, kz]T,使其取值靠近0.5,以减小pr收缩过程中的最大速度.

综上所述,τVFG制导矢量的表达式为

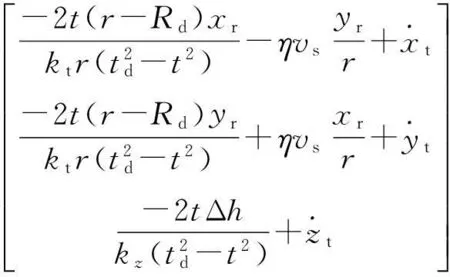
(12)

当t→td时,τ(pr)→0,在目标圆上仅S(pr)发挥作用,UAV以应飞速度绕目标旋转.τVFG是时变的矢量场,其在制导中融入了时间信息,可为各时刻、各位置的UAV提供合适的制导矢量.

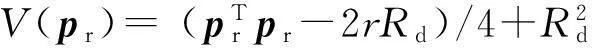
(13)

(14)

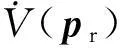
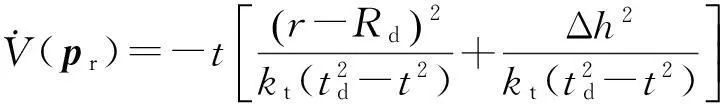
(15)

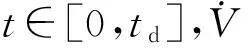
图4　基于τVFG的无人机standoff跟踪移动目标Fig.4　Standoff tracking of moving target based on τVFG

不同时刻的τVFG和UAV飞行轨迹示例如图 4所示,其中UAV初始位置为[-400,-400]m,应飞速度vd=30m/s,目标初始位置为[0,0]m,以[3,3]m/s的速度匀速运动,期望跟踪形成时间td=50s.由图 4和式(12)可知,在tau矢量场制导的作用下,无论UAV位于目标圆内部还是外部,都能在时间td收敛于目标圆并环绕目标飞行,有效弥补了LVFG等方法不能严格满足时间约束的缺陷.在standoff跟踪形成后的跟踪保持段,应当设定任务的期望时间td为较小值,以及时闭合UAV与目标圆之间的间距,保持对运动目标的跟踪.

3多机协同standoff跟踪方法

3.1多UAV协同相位调整

在多UAV协同跟踪任务中,为使多架UAV按一定相位间隔分布在目标圆上,当旋转项S(pr)不能提供合适的相位调整角速率时,需要在S(pr)上增加相位调整补偿速度.

设i、j2架UAV间的相位间隔为θij,期望间隔为θdij,偏差Δθij=θdij-θij.与τVFG相似,采用tau-G制导策略描述t→td时,θij→θdij的过程,间距闭合所需的角速率为

(16)

式中:Δθ0ij为相位调整初始时刻相位偏差,kθ ij为相位间隔调整的耦合系数.在时刻t,Δθ0ij根据Δθij求得.

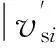
(17)

3.2多UAV协同避碰避障

多UAV在位置收敛和相位调整过程中,可能会发生冲突或遇到障碍,因此需要对冲突进行检测,并对制导策略U进行修正,以保证飞行安全.

在多UAV协同跟踪过程中,各UAV不能被当作质点,因此在冲突检测中应当考虑UAV的形状和体积.本文采用为UAV分配球形安全飞行区的方法[19]进行冲突检测,如图 5所示,安全区的半径Rsafe应大于等于UAV的安全飞行距离,当其他UAV或障碍进入安全区(满足式(18)),将会产生冲突报警；[xc,yc,zc]为闯入者相对于UAV本机中心的位置.该检测方法可提供明确的安全警报,且检测效率高,目前在航迹规划领域已经得到了广泛应用.简便起见,本文中假设障碍物在UAV飞行高度的水平面内投影为圆形.

(18)

图5　基于人工势场法的UAV避障策略Fig.5　Obstacle avoidance based on Artificial Potential Field

为消解跟踪过程中存在的冲突,本文采用人工势场法导引UAV绕开冲突位置.该冲突消解方法采用虚拟势场填充多UAV的工作空间,并利用势函数求出障碍和其他UAV对本机作用的虚拟合力矢量,而后根据虚拟力的作用调整τVFG矢量航向的方法进行避障,即将制导策略U绕z轴旋转Δψ变为U′.本文所采用的势场仅考虑斥力,当UAV与障碍或其它飞机的距离d≤Ravoid时,斥力Frep发生作用；反之斥力为0；‖Frep‖的表达式为

(19)

式中:μ为角度调整增益,α为较小正数,以避免d→Rsafe时‖Frep‖→∞.

在障碍势场的作用下,UAV所受到的虚拟力Frep及避障策略如图 5,其方向沿障碍距UAV最近的点与UAV中心的连线指向UAV.将Frep分解为沿UAV运动方向的径向力Famp和法向力Fort,其中‖Famp‖决定了航向角修正量Δψ的大小(Δψ∈(-π/2,π/2)),Fort的方向决定了Δψ的方向.修正量Δψ的表达式为

(20)

UAV距障碍越近,Δψ也越大；当UAV远离障碍直至d>Ravoid时,Δψ为0.在虚拟力的作用下,UAV可以避免在跟踪与相位调整过程中发生碰撞.存在障碍的τVFG示例如图 6所示,从中可以观察出障碍对矢量场制导方向的影响.

图6　存在障碍的τVFGFig.6　 τVFG case with obstacle

3.3多机协同standoff跟踪算法完整流程

在协同跟踪过程中,各UAV需快速响应跟踪,尽快运行至目标圆附近,且制导策略应符合UAV的应飞能力.由图 2可知,通过对τVFG的耦合系数矢量k=[kt,kz,kθij]T的选取可以获得期望的运动状态间距闭合过程；因此在跟踪的初始时刻,各UAV首先根据自身情况求解如下局部优化问题：

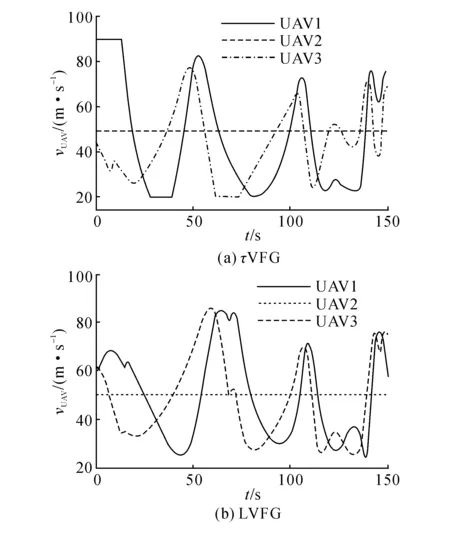
S.t.0

(21)

式中:Ji表示若以UAVi的位置、相位间隔闭合过程中的最大速度运行,达到目标状态所需的平均时间,约束条件包括耦合系数的取值范围和最大速度、转弯角速率、爬升/下滑率的限制.由式(13)、(15)对τVFG制导策略的稳定性分析可知,对耦合系数矢量k的优化不会影响τVFG能够严格按照时间约束导引运动状态间距平稳闭合的特性；且式(21)所示优化问题仅考虑跟踪响应的快速性和UAV的动力学约束,不会对算法的一般性带来影响.本文采用序列二次规划方法对k进行优化求解.在standoff跟踪过程中,除‖U‖≥vamax外,不对k进行重新选取.

在每个控制周期,各UAV首先根据τVFG计算矢量场制导策略,而后根据角度间隔情况对旋转项进行补偿,最后判断是否存在冲突并进行消解.

综上所述，包含τVFG、多UAV协同相位调整、协同避碰避障的多机协同standoff跟踪方法的完整流程如下：

1初始化各UAV的τVFG耦合系数矢量k

2 for 每个控制周期 do

3for 每一架UAV (i=1…N)do

4根据pri和时刻t依式(12)计算Ui

5根据与相邻UAV的角度间隔依(17)调整Si(pr)

6根据距障碍和其它UAV距离计算Δψi,并旋转Ui

7end for

8end for

4仿真结果与分析

目前针对多UAV协同standoff跟踪问题尚未有标准测试用例,因此本文采用包含运动目标协同跟踪,相位间隔调整,避障等任务的仿真对基于τVFG的standoff跟踪算法性能进行验证,并与目前standoff跟踪中应用最广泛的LVFG进行对比.

在仿真任务中,3架同型UAV协同对三维运动目标进行跟踪,各UAV应飞速度vd=50 m/s,初始位置分别为p1=[-400,-400,20] m,p2=[400,-400,40] m,p3=[400,400,200] m,其余指标包括：vamax=90 m/s,vamin=10 m/s,ωmax=5 °/s,λmax=5 m/s.运动目标初始位置为pt=[0,0,0],在水平面内运动速度vt和运动方向ψt的变化如表 1所示,垂向运动速度为vtz=2 m/s.目标圆半径为Rd=300 m,高度Hd=0 m,UAV之间期望相位间隔θd12=-2π/3,θd32=2π/3,安全间距Rsafe=25 m,跟踪形成期望时间td=100 s,跟踪保持段td=5 s.全部仿真实验采用Matlab/Simulink R2013a设计,在有2.6GHz Core i5-3230M CPU和4GB RAM的计算机完成.

表1　目标运动速度和方向

图7　τVFG作用下的UAV航迹Fig.7　UAV paths guided by τVFG

表2不同制导方法性能对比

Tab.2Performance comparison between the methods based onτVFG and LVFG

制导方法tc/(10-4s)perr/mθerr/(°)τVFG4.160.280.34LVFG6.886.201.27

图8　各UAV距目标距离随时间变化情况Fig.8　Distances between UAVs and moving target

图9　各UAV相位间隔Fig.9　Phase differences between different UAVs

在跟踪过程中各UAV的飞行速度vUAV如图 10所示,因为UAV1和UAV3承担了角度间隔调整的任务,同时目标在不断变速运动,因而其速度并未保持应飞速度vd.由图 10(a)、(b)对比可知,τVFG所提供的制导速度始终在vamax和vamin之间,而LVFG的制导速度则超出了UAV的飞行能力而被限幅.

各UAV与障碍之间的最小距离(d01,d02,d03)如表 3所示,τVFG可导引UAV安全地完成跟踪任务,距障碍的距离大于安全飞行间距Rsafe=25 m,而LVFG则不能保证UAV的飞行安全,UAV1、UAV2均与障碍发生碰撞.在飞行过程中,各UAV之间均保持了安全飞行距离,未发生碰撞,此处不再赘述.

图10　各UAV飞行速度Fig.10　Velocities of UAVs

制导方法d01/md02/md03/mτVFG27.130.527.8LVFG7.24.229.5

5结语

本文针对已有矢量场制导方法无法满足standoff跟踪中时间约束的缺陷,将时间信息融入矢量场中,利用广义tau理论的tau-G制导策略构建了四维tau矢量场制导(τVFG),可导引UAV的位置严格按照期望时间收敛于目标圆.在多UAV协同standoff跟踪应用中,用tau-G策略调整UAV之间的相位间隔,采用人工势场法进行协同避碰避障,并运用序列二次规划对τVFG和相位调整进行参数优化.与LVFG对比的仿真结果表明,本文所提出的方法具在计算负荷、跟踪偏差、制导策略的可飞性、飞行安全性等方面均明显占优,能够更好地满足多UAV协同standoff跟踪的任务需求,同时也扩展了广义tau理论在UAV领域的应用范围.

在未来的工作中,将在τVFG中考虑包括UAV初始航向在内的更多约束,使τVFG应用于更多UAV协同跟踪任务场景中.

参考文献(References)：

[1] FREW E W, LAWRENCE D A, MORRIS S. Coordinated standoff tracking of moving targets using lyapunov guidance vector fields [J]. Journal of Guidance, Control, and Dynamics, 2008, 31(2): 290-306．

[2] WISE R A, RYSDYK R T. UAV coordination for autonomous target tracking [C]∥ Proceedings of the AIAA Guidance, Navigation, and Control Conference, Keystone: AIAA, 2006: 21-24．

[3] OH H, TURCHI D, KIM S, et al. Coordinated standoff tracking using path shaping for multiple UAVs [J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(1): 348-363．

[4] KIM S, OH H, and TSOURDOS A. Nonlinear model predictive coordinated standoff tracking of a moving ground vehicle [J]. Journal of Guidance, Control, and Dynamics, 2013, 36(2): 557-566．

[5] 王树磊,魏瑞轩,郭庆,等. 面向协同standoff跟踪问题的无人机制导律 [J]. 航空学报,2014,35(6): 1684-1693.

WANG Shu-lei, WEI Rui-xuan, GUO Qing, et.al. UAV guidance law for coordinated standoff target tracking [J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(6): 1684-1693．

[6] LAWRENCE D A. Lyapunov Vector Fields for UAV Flock Coordination [C]∥ 2nd AIAA “Unmanned Unlimited” Conf. and Workshop & Exhibit.[S.l]: AIAA, 2003.

[7] CHEN H, CHANG K, AGATE C S. A dynamic path planning algorithm for UAV tracking [C]∥ Proceedings of SPIE Signal Processing, Sensor Fusion, and Target Recognition XVIII. Orlando: SPIE, 2009: 1-10．

[8] CHEN H, CHANG K, AGATE C S. UAV path planning with tangent-plus-Lyapunov vector field guidance and obstacle avoidance [J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2): 840-856．

[9] LEE D N. A theory of visual control of braking based on information about time-to-collision [J]. Perception, 1976, 5(4): 437-459．

[10] LEE D N, REDDISH P E. Plummeting gannets: a paradigm of ecological optics [J]. Nature, 1981, 293(1): 293-294．

[11] LEE D N, DAVIES M N, GREEN P R. Visual control of velocity of approach by pigeons when landing [J]. Journal of Experimental Biology, 1993, 180(1): 85-104．

[12] HECHT H ,SAVELSBERGH G J. Time-to-contact [M]. Amsterdam: Elsevier, 2004．

[13] LEE D N. General tau theory: evolution to date [J]. Perception, 2009, 38(6): 837-858．[14] 张书涛,张震,钱晋武. 基于Tau理论的机器人抓取运动仿生轨迹规划 [J]. 机械工程学报,2014,50(13): 42-51.

ZHANG Shu-tao, ZHANG Zhen, QIAN Jin-wu. Bio-inspired trajectory planning for robot catching movements based on the tau theory [J]. Journal of Mechanical Engineering,2014, 50(13): 42-51．

[15] KENDOUL F. Four-dimensional guidance and control of movement using time-to-contact: Application to automated docking and landing of unmanned rotorcraft systems [J]. The International Journal of Robotics Research, 2014, 33(2): 237-267．

[16] ZHANG Z, XIE P, MA O. Bio-inspired trajectory generation for UAV perching movement based on tau theory [J]. International Journal of Advanced Robotic Systems, 2014, 11(1): 1-13．

[17] BOUSSON K ,MACHADO P F F. 4D trajectory generation and tracking for waypoint-based aerial navigation [J]. WSEAS Transactions on Systems & Control, 2013, 8(3): 105-119．

[18] SCHOGLER B, PEPPING G J, LEE D N. TauG-guidance of transients in expressive musical performance [J]. Experimental Brain Research, 2008, 189(3): 361-372．

[19] GOSS J, RAJVANSHI R, SUBBARAO K. Aircraft conflict detection and resolution using mixed geometric and collision cone approaches [C]∥ AIAA Guidance, Navigation, and Control Conference and Exhibit. Providence: AIAA, 2004: 1-20．

Cooperative standoff tracking for multi-UAVs based on tau vector field guidance

YANG Zu-qiang1, FANG Zhou1, LI Ping1,2

(1.SchoolofAeronauticsandAstronautics,ZhejiangUniversity,Hangzhou310027,China;2.CollegeofControlScienceandEngineering,Hangzhou310027,China)

Abstract:A four dimensional (4D) vector field guidance (VFG) method was presented for time-constrained cooperative standoff tracking of multiple unmanned aerial vehicles (UAVs). The tau VFG (τVFG) was proposed utilizing the 4D synchronous guidance capability of the intrinsic tau gravity (tau-G) guidance strategy. A comprehensive standoff tracking method was designed for multiple UAVs with the help of τVFG. The τVFG was applied to guide UAVs to approach the standoff circle exactly at the desired time, and tau-G guidance was also adopted for phase intervals adjustment. Tracking parameters were optimized by sequential quadratic programming, and conflicts were resolved by artificial potential fields. Simulation results show that the τVFG-based method performs better in cooperative standoff tracking tasks with a lower computation load, smaller tracking errors, better flyability and higher flight safety.

Key words:general tau theory; tau vector field guidance; standoff tracking; multi-UAV coordination

收稿日期：2015-10-17.浙江大学学报(工学版)网址： www.journals.zju.edu.cn/eng

基金项目：国家自然科学基金资助项目(61004066);浙江省自然科学基金资助项目(LY15F030005);浙江省公益性技术研究计划资助项目(2016C33246).

作者简介：杨祖强(1989-),男，博士生，从事多无人机协同规划方法，飞行器控制与仿真桨研究.ORCID:0000-0001-5272-0390.E-mail:gaayzq@zju.edu.cn

通信作者：方舟，男，副教授.ORCID:0000-0002-0733-958X.E-mail:zfang@zju.edu.cn

DOI:10.3785/j.issn.1008-973X.2016.05.024

中图分类号：V 249

文献标志码：A

文章编号：1008-973X(2016)05-0984-09