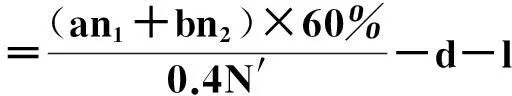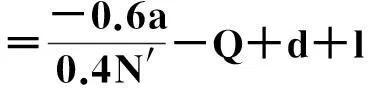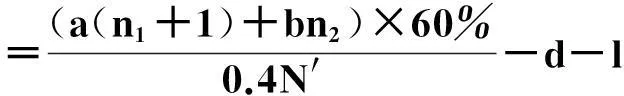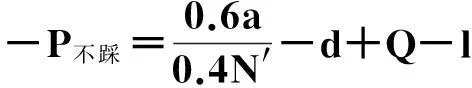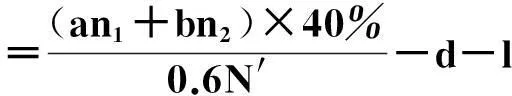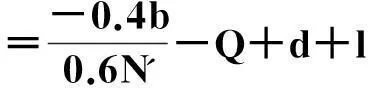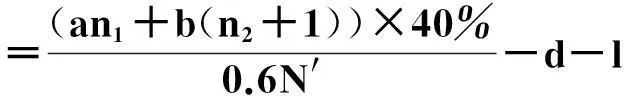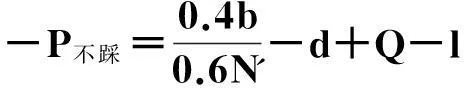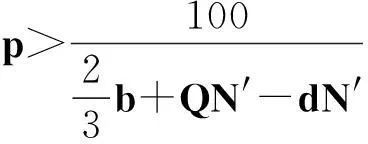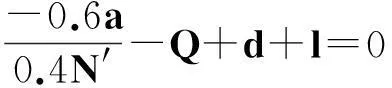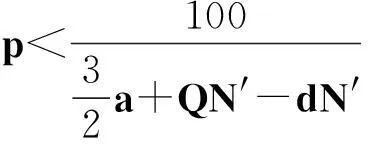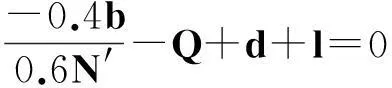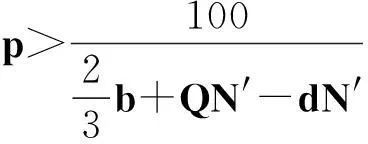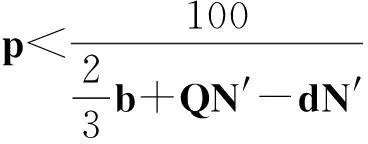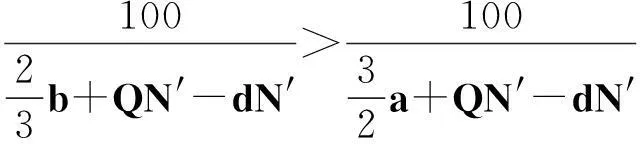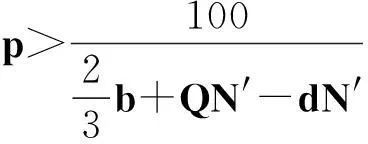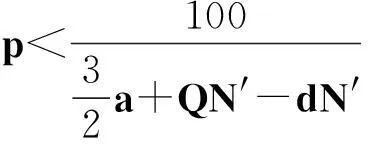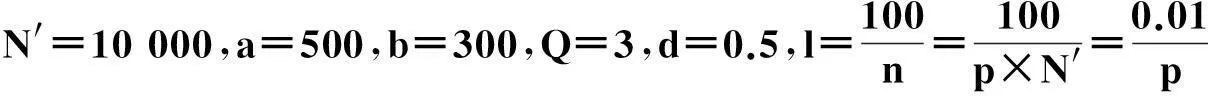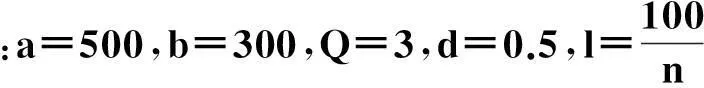多人智猪博弈及其在羊群模型中的应用
周明华,郑婷婷,陆 川,孙长启
(浙江工业大学 理学院,浙江 杭州 310023)
多人智猪博弈及其在羊群模型中的应用
周明华,郑婷婷,陆川,孙长启
(浙江工业大学 理学院,浙江 杭州 310023)
摘要:在原始双人智猪博弈模型的基础之上,引入惩罚因子和反省机制,提出了一个N人扩展智猪博弈模型.由于在现实的金融市场中经纪人的能力存在差别,因此将N人扩展智猪博弈与羊群模型相结合,提出了一个带有智猪博弈的羊群模型,使得当经纪人做决策时并不是单一地选择跟随.最后,对该模型进行了实验仿真,实验结果表明:带有智猪博弈的羊群模型能较好得反应金融市场的行为和特性.
关键词:智猪博弈;羊群模型;惩罚因子;反省机制
在博弈论经济学中,智猪博弈是一个经典的模型.1979年动物心理学家Baldwein和Meese做了一个著名的实验[1]:在猪圈里放一大一小两头猪,在猪圈的一头装一个控制猪食的拱杆,另一头装一个供应食物的实槽,每拱一次拱杆食槽中便会有食物落下.经过多次博弈之后,达到一个均衡状态:大猪出力,小猪搭便车.1989年,E.Rasmusen[2]将该现象引进博弈论,提出了原始的智猪博弈模型.目前,该模型的研究都是在原始双人智猪博弈模型的一些条件上进行改进[3-4],以及该博弈模型的一些实际应用[5-6].但是,考虑到实际情况中,博弈个体往往是多方的,如团体内个体间的博弈,此时,原始智猪博弈的应用存在一定的局限性,为了克服这种局限性,在双人博弈模型的基础上对此进一步改进,提出了一个带有惩罚因子的N人扩展智猪博弈模型,使得智猪博弈模型的应用能更为广泛.
近年来,随着行为金融学和计量经济学被广泛认知,学者们对投资者行为及金融时间价格收益率的研究也愈来愈热.Eguiluz和ZimmermannEZ[7]在Physical Review Letters中提出了一个羊群模型,从金融市场的微观机理上解释了金融时间价格的收益率为何存在尖峰胖尾的现象,从而获得了许多学者的重视.从此,羊群模型的研究及应用迅速引起了相关学者的兴趣.目前许多学者都对羊群模型做了更深入的研究,如郑波,董林荣,Arne C.Klein等[8-16].我们发现,目前已有的研究羊群行为的各种模型,大都遵循EZ羊群模型的提出的同一个集团中的经纪人会因为羊群行为而采取相同策略的假设,但是这一假设过于理想化.根据现实的金融市场,由于集团内的各经纪人得到不同的信息,拥有多样化的资源,他们的认知能力,判断能力,心理因素等都存在着或多或少的差异,因而同一集团中的经纪人做决策时,并非所有人都选择跟随,经纪人与经纪人之间会有一个相互博弈的过程.因此,为了更贴近现实的金融市场,我们将多人智猪博弈模型与羊群模型结合,提出了一个带有多人智猪博弈的羊群模型,并对其进行了仿真分析.仿真结果表明:带有智猪博弈的羊群模型符合现实金融市场的程式化规律.
1N人扩展智猪博弈模型
1.1原始智猪博弈简介
在智猪博弈(Boxed pigs)中,假设猪圈里有两头猪,一头大猪,一头小猪.猪圈的一边是一个供应食物的食槽,另一边是一个控制食槽中食物供应的踏板.当有猪踩踏板时,位于另一头的食槽就会有一份食物落下.若小猪选择踩踏板,大猪会在小猪跑到食槽前吃光一整份食物;若大猪选择踩踏板,小猪只能在大猪到达前时吃掉半份食物.并且假设大猪吃的速度是小猪的两倍,大小猪跑路均需要消耗一份食物1/4的能量.表1为其支付矩阵.在支付矩阵中,我们注意到,不论大猪怎么选择,等待均是小猪的最优选择.因为,若大猪踩踏板,小猪如果也踩踏板则收益为1/12,选择等待的收益为8/12;若给定大猪等待,小猪选择踩踏板的收益为-1/4,选择等待则是0.所以等待是小猪的占优策略.在小猪总是选择等待的情况下,踩踏板是大猪的最优选择.所以,纳什均衡是:大猪踩踏板,小猪等待.

表1 智猪博弈支付矩阵
1.2N人扩展智猪博弈模型
由于在现实世界中博弈方往往不止两个,比如金融市场中的经纪人.由此提出了一个N 人扩展智猪博弈模型.
该模型假设:一个猪圈中共有N′ 头猪,其中大猪N1头,小猪N2头,并且假设N1=0.4N′,N2=0.6N′,即N1+N2=N′.其中踩踏板的大猪有n1头,踩踏板的小猪有n2头,n表示踩踏板的猪的总数,即n=n1+n2.在初始状态下选择踩踏板的概率为p.a为一只大猪踩踏板落下的食物,b为一只小猪踩踏板落下的食物(a>b),选择踩踏板的猪需要消耗的能量为d.由于考虑到实际情况中博弈者做出决策往往需占用或使用如资金、材料而引起应当支付的费用,或需付出一定的时间代价,以及在这等待时间中造成的市场机会的丢失等等,而这时的时间成本会随着决策人数的变化而变化,当做决策的博弈者越多时,所需付出的时间成本越少.为了简化计算,笔者使用了反比例函数来计算时间成本,记需要消耗的时间成本为 l=α/n(α为一个常数).若不踩踏板,还需要受到一定的惩罚,引进惩罚因子Q.则集团的总收益为an1+bn2.由于大猪的吃食速度大于小猪的吃食速度,则可假设所有大猪可获得总收益的60%,小猪获得总收益的40%.因此可得2种收益函数:
1) n=0时,P=0(即所有猪的收益均为0).
2) n≠0时,分别考虑大猪与小猪的情况,即
(1)大猪:
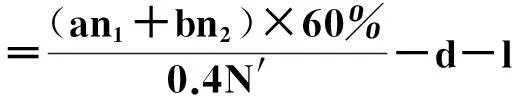
(2)小猪:

在博弈中假设行为主体具有完全理性思维,即所有参与者都是理性的,并且所有参与者知道其他参与者也都是理性的,这在实际情况中,对于行为主体的认知能力而言是一项非常严格的假设,通常得不到保证.在该假设下,只要纳什均衡存在,不需要任何的动态调整过程,只需博弈一次就可以直接达到纳什均衡,这显然不符合现实的市场.因此笔者进而引进了一个演化机制下的N 人扩展智猪博弈模型,该模型中假设行为主体是有限理性的,他们无法在博弈中瞬间获得最优的结果,而是在博弈过程中不断的修正和改进的,这是一个动态的调整过程.这与现实情况更符合.
1.3演化机制下的N人扩展智猪博弈
在演化博弈中,通常代理人需要按照一定的规则对他们的使用策略进行更换,采用“自我反省”的机制进行更换.所谓反省机制,即单轮博弈结束后,代理人可以获悉此轮博弈中的合作代理人数,不合作代理人数,通过计算采取相反策略获得的虚拟收益(PV)与实际收益(PR)的差别来决定下一轮博弈中采取何种策略:如果PR>PV,下一轮博弈中代理人不改变策略;若PR 在反省机制下,多人智猪博弈可分为4 种情况(n≠0时): 1) 大猪实际踩踏板: 2) 大猪实际不踩踏板: 3) 小猪实际踩踏板: 4) 小猪实际不踩踏板: 证明:令ΔP1=0,则 得证. 1.4模型仿真分析 图1 智猪博弈关于p的演化Fig.1 Evolution of boxed pigs game on p 2带有多人智猪博弈的羊群模型 考虑到实际的金融市场中经纪人的能力存在差异,如决策能力,判断能力等,正如智猪博弈中的大猪与小猪的区别.在决策过程中,一个集团的经纪人,并不是所有人选择跟随,从而均采取相同的策略,经纪人相互间有一个博弈的过程,以判断是否采取跟随策略,因此提出了一个带有智猪博弈的羊群模型.我们将集团中能力较强,拥有资源较多的经纪人视为大猪,将其余的经纪人视为小猪,因无法具体甄别个体与个体间的差别,因此随机选出集团中40%的经纪人视为大猪.则此时集团间的博弈即多人智猪博弈.该模型包含了N个人的经纪人系统,经纪人的状态用φl={0,+1,-1}表示(0表示等待,+1表示买入,-1表示卖出),其初始条件与EZ羊群模型相同.各经纪人在初始状态下均处于等待状态(φl=0,∀l),此时各经纪人都是独立的(每一个经纪人构成了一个集团).在接下来的某一时刻t: 1) 随机选择一个经纪人i. 2) 判断经纪人i所在集团的规模是否大于1. (2) 若等于1:(a) 经纪人以概率p选择交易,继而随机选择择φi取+1或-1,接着经纪人i依旧保持独立状态;(b) 经纪人i以概率(1-p)选择等待,此时,随机选择i所在集团外的择经纪人j,i与j所在的集团合并为更大的集团. 2.1仿真结果 为了更全面地考察带有智猪博弈的羊群模型是否符合现实金融市场,我们用Matlab编程对其进行模拟. 在计算过程中,具体计算公式为 P(t+1)=P(t)est/λ R(t)=ln[P(t)]-ln[P(t-1)] 通过Matlab编程进行动态模拟,得到集团中经纪人规模的频率分布,收益率分布及其规范化收益率分别如图2~5所示. 图2 参与交易的集团中经纪人规模的频率分布图Fig.2 Plot of distribution of size of agents in the cluster belonging to trade 图3 收益率R分布示意图Fig.3 Plot of distribution of return R 图4 规范化收益率分布图Fig.4 Plot of distribution of normalized return 图5 规范化收益率stR频率分布的双对数图Fig.5 Log-log plot of distribution of normalized return stR 如图2~4所示,参与交易的集团中经纪人规模的频率分布,收益率R分布,规范化收益率分布均呈现出尖峰胖尾现象,这与实际金融市场中的动力学特征相符合.由图5可知:规范化收益率的概率呈幂次率分布,通过拟合,得到幂次率的斜率约为4.2,这符合真实的市场规律[12].这在一定程度上说明:带有N人智猪博弈的羊群模型符合现实金融市场的程式化规律. 3结论 现实博弈中的参与者往往是多人,而不仅仅是两个人,根据对现实情况的考虑,笔者对原始智猪博弈进行了一些修改,提出了一个带有惩罚因子和反省机制的N人扩展智猪博弈,并对该模型进行了Matlab仿真.随即针对现实金融市场中各经纪人的的能力存在差别(即进行大猪与小猪的区分),在集团做决策时并不是盲目地跟随而是有选择性地选择跟随,因此将N人智猪博弈与羊群模型相结合,提出了一个带有N人智猪博弈的羊群模型,使得羊群模型更具有实际意义,并且对该模型进行了动态模拟,仿真结果表明:此模型符合现实金融市场的程式化规律. 参考文献: [1]BALDWIN B A, MEESE G B. Social behavior in pigs studied by means of operant conditioning[J]. Animal behavior,1979,27(3):947-957. [2]RASMUSEN E. Games and information: an introduction to game theory[J]. Basil blackwell,1989,9(3):841-846. [3]蒋梦晴,姜殿玉.基于踏板时间的智猪博弈吃食量与Nash均衡集合研究[J].淮海工学院学报,2012,21(1):1-6. [4]吴航.智猪博弈与改进[J].商情,2014(7):79-79. [5]陈永宇.“智猪博弈”模型改进与团队激励策略研究[J].人才开发,2009(6):19-21. [6]邓明然,吴艳.“智猪”博弈在中小企业模仿创新中的应用[J].文教资料,2006,25:189-190. [7]EGUILUZ V M, ZIMMERMANN M G. Transmission of information and herd behavior: an application to financial markets[J]. Physical review letters,2000,85:5659-5662. [8]ZHENG B, REN F, TRIMPER S, et al. A generalized dynamic herding model with feed-back interactions[J]. Physica a statistical mechanics & its applications,2004,343:653-661. [9]DONG L R. Interacting herding model: memory and oblivion[J]. Acta physica sinica,2006,55(8):4046-4050. [10]DONG L. Volatilities and desires of the agent clusters drive together markets[J]. Physica a statistical mechanics & its applications,2007,380(7):512-518. [11]余义龙,成丹丹,刘鸿鸣,等.具有长程记忆和市场判断力的异质经纪人Herding模型[J].浙江工业大学学报,2011,39(2):231-236. [12]余义龙.金融市场中羊群行为的研究[D].杭州:浙江工业大学,2010. [13]KLEIN A C. Time-variations in herding behavior: evidence from a Markov switching SUR model[J].Journal of international financial markets, institutions and money,2013,26(2):291-304. [14]HUANG T C, LIN B H, YANG T H. Herd behavior and idiosyncratic volatility[J].Journal of business research,2015,68:763-770. [15]DEMIRER R, LEE H T, LIEN D. Does the stock market drive herd behavior in commodity futures markets?[J]. International review of financial analysis,2015,39:32-44. [16]周明华,陆川,俞伟,等.一个随集团规模改变的集团部分分解羊群模型[J].浙江工业大学学报,2015,43(1):115-118. (责任编辑:陈石平) N-person boxed pigs game and its application in the herding model ZHOU Minghua,ZHENG Tingting,LU Chuan,SUN Changqi (College of Science, Zhejiang University of Technology, Hangzhou 310023, China) Abstract:In this paper, the penalty factors and reflection mechanism is introduced and an N-person Boxed Pigs model on the basis of the original Boxed Pigs is proposed. In fact, different agents in real financial markets may have different abilities. The article puts forward a model which is called herding model with the boxed pigs, combining the N-person Boxed Pigs model and the herding model. It gives the agents more choices while they make decisions. Finally, the model is simulated. The experiments show that the behaviors and characteristics of financial markets can be better reflected by the herding model with Boxed pig. Keywords:boxed pigs; herding model; penalty factor; reflection mechanism 收稿日期:2015-10-12 基金项目:浙江省自然科学基金资助项目(LQ16A010008) 作者简介:周明华(1959—),男,浙江绍兴人,教授,研究方向为金融数学,E-mail:mhzhou@zjut.edu.cn. 中图分类号:F832.48 文献标志码:A 文章编号:1006-4303(2016)02-0231-06