基于GPU的SSOR稀疏近似逆预条件研究
高家全,王志超
(浙江工业大学 计算机科学与技术学院,浙江 杭州 310023)
基于GPU的SSOR稀疏近似逆预条件研究
高家全,王志超
(浙江工业大学 计算机科学与技术学院,浙江 杭州 310023)
摘要:由于SSOR预条件共轭梯度算法中预条件方程求解需要前推和回代,导致算法迁移到GPU平台上并行效率不高.为此,基于诺依曼多项式分解技术,提出了一种GPU加速的SSOR稀疏近似逆预条件子(GSSORSAI).它不仅保持了原线性系统系数矩阵的稀疏和对称正定特性,而且预条件方程求解仅需一次稀疏矩阵矢量乘运算,避免了前推和回代过程.实验结果表明:在NVIDIA Tesla C2050 GPU上,对比使用Python在单个CPU上SSOR稀疏近似逆预条件子实现方法,GSSORSAI平均快将近100倍;应用到并行的PCG算法中,相比无预条件的CG算法,平均提高了算法的3倍的收敛速度.
关键词:SSOR预条件子;预条件共轭梯度算法;稀疏近似逆;GPU
求解稀疏对称正定的线性系统Ax=b是科学计算和工程应用的核心问题.一般采用迭代法求解,其中共轭梯度 (Conjugate gradient, CG) 算法是目前流行的解此类线性系统的迭代法之一[1-2].与其他迭代法一样,CG算法的性能和效率依赖于线性系统的系数矩阵条件数的好坏,坏的系数矩阵条件数将会导致CG算法收敛慢或不收敛[1-4].为解决这方面的问题,求解线性系统之前需进行预处理.预处理技术就是构造一个预条件子M,使得Max=Mb或者AMy=b,x=My.选择合适的预条件子能够减少算法的迭代次数进而减少其执行时间.SSOR (Symmetric successive over-relaxation) 预条件子用于CG算法的预处理已证明是有效的,然而由于SSOR预条件方程求解需要前推和回代过程,很难进行并行化处理,这很大程度上降低了SSOR预条件CG (PCG) 算法解决大规模线性系统的性能和效率[3-4].
基于诺依曼(Neumann)多项式分解技术,提出了一种SSOR稀疏近似逆预条件子,并在GPU (Graphic processing unit)上并行实现.提出的SSOR稀疏近似逆预条件子的主要运算由矩阵求和与两矩阵相乘组成,易于并行实现,而且应用于PCG算法,预条件方程求解仅需一个稀疏矩阵矢量乘运算,避免了SSOR预条件子的前推和回代过程.笔者主要做了如下几个贡献:首先提出了一种SSOR稀疏近似逆预条件子,不仅保持了稀疏性,而且还保证了其对称正定特性;然后探讨了SSOR一阶和二阶稀疏近似逆的性能,并给出了高效的GPU并行实现算法;最后应用于PCG算法,验证了其有效性.
1SSOR近似逆预条件子
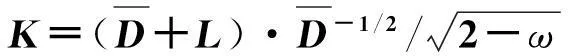
(1)
为保证其稀疏性,给出了如下方案:如果

(2)

为简便,仅讨论SSOR一阶近似逆和二阶近似逆两种情况.
2GPU实现
基于CUDA,设计了一个有效的SSOR稀疏近似逆预条件子计算框架(图1).框架分初始化、计算和应用三个阶段.
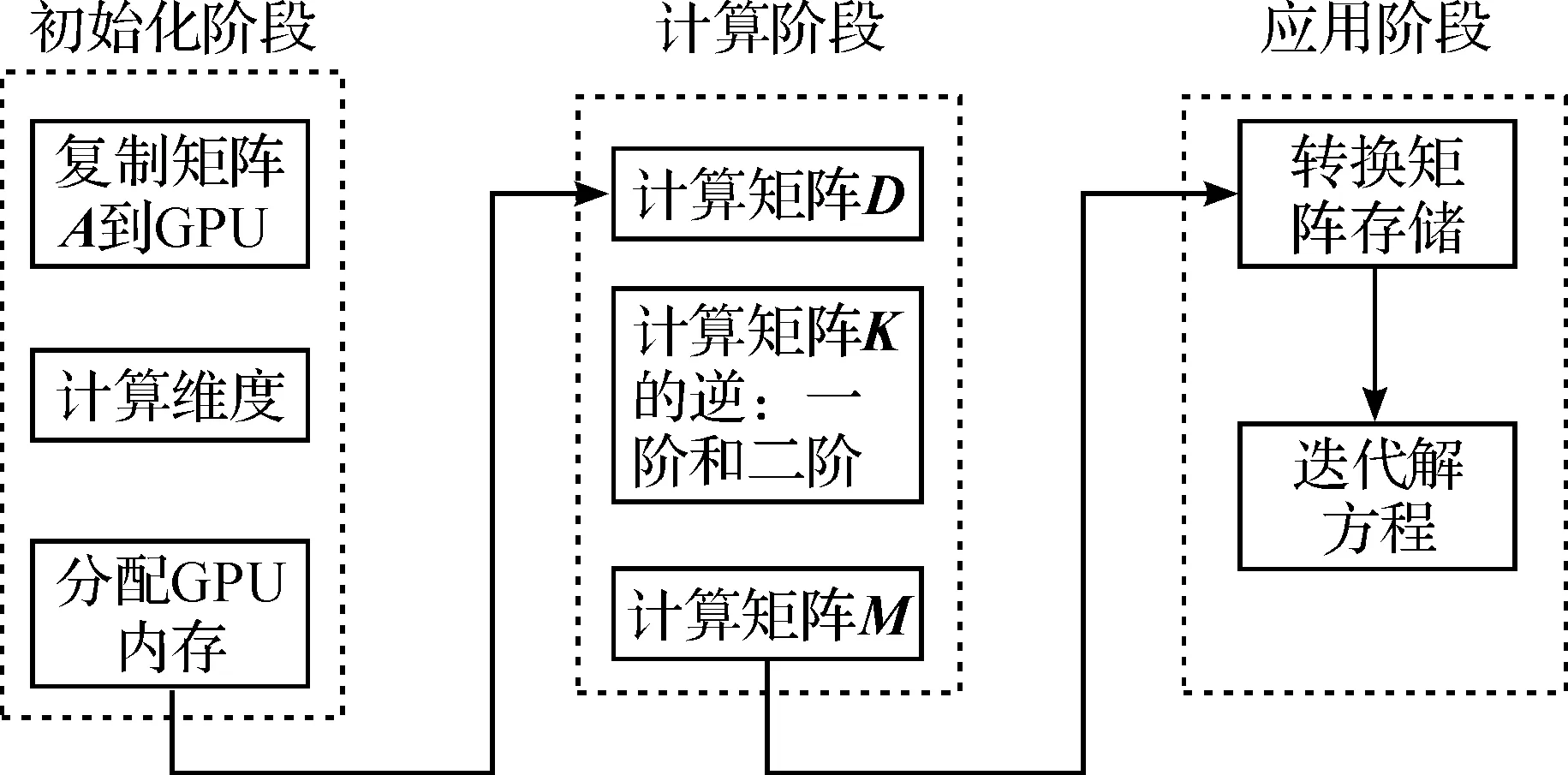
图1 计算框架Fig.1 The computing architecture
2.1初始化
首先复制矩阵A到GPU.对于稀疏矩阵A,为提高运算效率和节省存储空间,采用CSR的压缩存储方式[9-10].

2.2计算阶段

首先计算对角矩阵D.对角矩阵D由矩阵A的对角元素组成,核函数设计如下:让每个线程 (Thead)负责寻找A的一行中的对角元素值,并存储到全局内存中.共需要Row(A的行数)个线程,如果每个线程块 (Block) 包含256个线程,则需要Row/256个线程块.
(3)

Input: A, K, M;
Output: M;
__shared__ P[];
//利用GPU中的线程、线程块和网格属性
tid←blockDim.x* blockIdx.x+ threadIdx.x;
lane←tid & 31;wid←threadIdx.x>> 5;row←wid;
forifrom K.mPtr[row] to K.mPtr[row+1] withi++
P[i] = K.mIndex[i];
end
forjfrom A.mPtr[row]+ lane to A.mPtr[row+1]withj+= 32
// Each element of M← one row of K * one column of K
column←A.mIndex[j];
forkfrom K.mPtr[column] to K.mPtr[column] withk++
forlfrom K.mPtr[row] to K.mPtr[row+1] withl++
//使用共享内存来提高计算速度
if(K.mIndex[k] == P[l])
dot←dot + K.mData[k] * K.mData[l];
break;
end
end
M.mData[j]←M.mData[j] + dot;
M.mIndex[j]←A.mIndex[j];
end



为解决内存访问不对齐,保证全局内存合并,减少内存交易 (Memory transaction) 次数,本研究采用了128对齐填充模式.假定A的前四行非零元素个数分别为12,26,8,16,并且精度为双精度 (Double)类型.从图2可以看出:填充前,共需7 次内存交易,然而填充后,前4 行的交易次数可以从7 次减小为5 次,进而提高了将近30%左右的内存访问效率.

图2 填充模式Fig.2 Padding scheme
2.3应用阶段
3实验和分析
这节将从如下几个方面来测试笔者提出的SSOR预条件子的一阶SSOR稀疏近似逆 (表示为M1) 和二阶SSOR稀疏近似逆 (表示为M2) 的性能: 1) 分析参数w和α对M1和M2性能的影响;2) 验证设计的SSOR稀疏近似逆算法的并行性;3) 应用到PCG算法中,来验证M1和M2的有效性.
在下面实验里, PCG算法的终止条件为最大迭代次数不多于5 000或残差小于10-12.所有的实验都执行在NVIDIA Tesla C2050 GPU上,测试矩阵来自Florida大学的稀疏矩阵集[12],表1给出了它们简要的描述.

表1 实验使用的矩阵类型
3.1实验分析
首先,测试稀疏性参数α对一阶SSOR稀疏近似逆M1和二阶稀疏SSOR近似逆M2性能的影响.为简便,在这个实验里,取w=0.8.表2给出了实验结果,每一栏对应α值的M1/ M2应用到PCG中算法收敛的迭代次数.迭代次数越少,表明获得的M1/ M2的性能越好.
从表2可以看出:对M1和M2来说,PCG收敛迭代次数一般随着α值的增加而减少.这意味着,一般情况下,只要取α=1.0时,保持M1和M2与A有着相同的稀疏结构时,M1和M2的性能最好.

表2 参数对M1和M2性能的影响1)
注:1) N/A表示迭代次数>5 000.
其次,调查w对M1和M2性能的影响.不失一般性,在这个实验里,取α=1.0,表3,4分别列出了w变化对应M1和M2的PCG算法收敛的迭代次数.同样,迭代次数越少,表明获得的M1/M2的性能越好.
从表3,4可以看出:类似于,w值的选取对M1和M2性能有影响,而且不同的w值,获得的M1/M2性能差异明显.因此,为得到最优性能的M1和M2,对给定的稀疏矩阵,最优w值的选取实验是必要的.
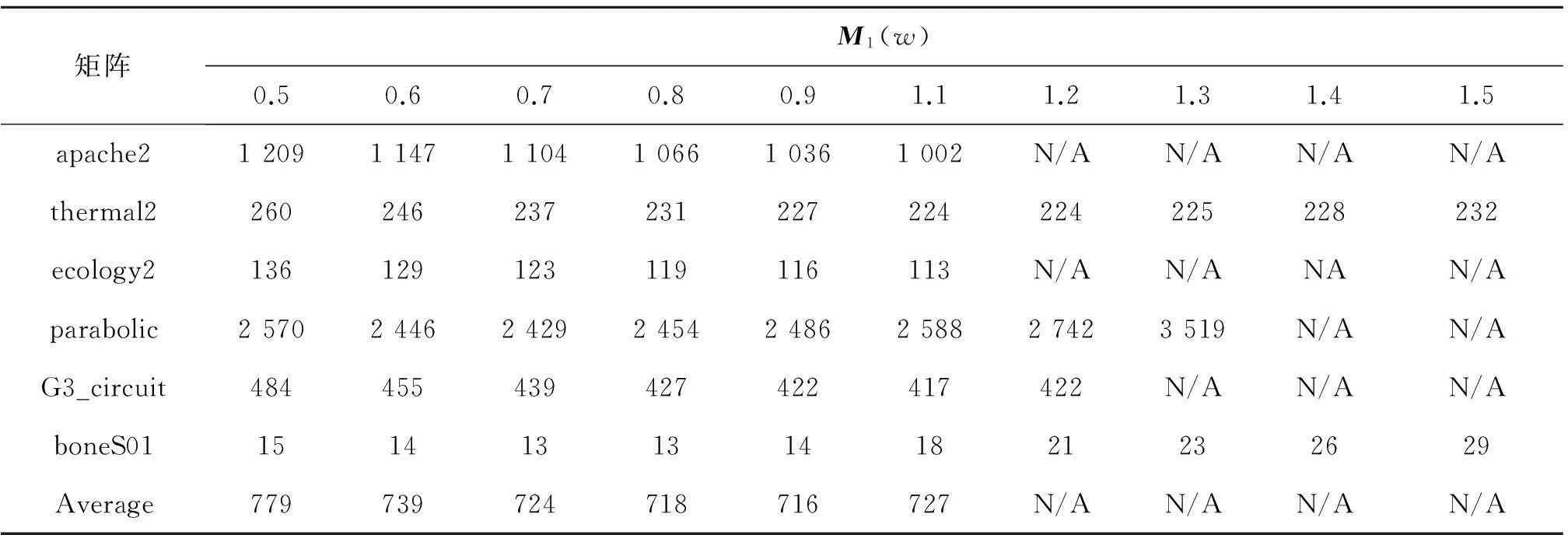
表3 参数w对M1性能的影响1)
注:1) N/A表示迭代次数>5 000.

表4 参数w对M2性能的影响1)
注:1) N/A表示迭代次数>5 000.
3.2SSOR稀疏近似逆算法的并行性
此节来测试提出的SSOR稀疏近似逆算法的并行性.从表3,4很容易计算出:为使用的6个测试矩阵,当α=1.0,w=0.9时,PCG平均迭代次数最小.不失一般性,这节实验取w=1.0 和α=0.9,分别计算一阶/二阶SSOR稀疏近似逆算法的GPU执行时间和对应串行CPU的执行时间 (串行的实现是基于编程模型Python).表5给出CPU和GPU执行时间的比较.

表5 CPU和GPU时间比较
从表5可以看出:一阶稀疏近似逆情况下,CPU与GPU的执行时间比率介于54.1~227之间,平均比率大约101;二阶稀疏近似逆情况下,CPU与GPU的执行时间比率介于43.4~220之间,平均比率大约90;总平均比率95.这表明本研究设计的GPU加速的一阶/二阶SSOR稀疏近似逆并行算法有着高度并行性.
3.3SSOR稀疏近似逆算法的性能
将M1和M2应用到PCG算法中,测试其性能.为每一个测试矩阵,α=1.0,w取表3,4中对应此测试矩阵平均迭代次数最小的w值.例如,对矩阵ecology2,取w=1.1.图3,4分别给出了GPU加速的CG算法、一阶SSOR稀疏近似逆PCG算法及二阶SSOR稀疏近似逆PCG算法的迭代次数和执行时间.时间单位为毫秒(ms).

图3 执行时间Fig.3 The execution time

图4 迭代次数Fig.4 The number of iterations
从图3,4可以看出:相对于直接CG算法,使用SSOR一阶/二阶稀疏近似逆预条件子后,PCG算法的迭代次数显著减少,而且执行时间也明显少于直接CG算法.这表明提出的SSOR一阶/二阶稀疏近似逆预条件子是有效的.相对于一阶稀疏近似逆预条件子M1,虽然取得二阶稀疏近似逆预条件子M2花费的时间略多(3.2节),但大大减少了PCG算法的迭代次数,进而减少了其执行时间.因此,可以断言,一般情况下,M2优于M1.
4结论
提出了一种GPU加速的SSOR稀疏近似逆预条件子,调研了一阶和二阶近似逆的有效性.为保证其稀疏性,提出了一种解决方案.为提高算法的性能,利用共享内存、内存访问合并及填充等策略进行优化.实验证明设计的SSOR稀疏近似逆预条件子是有效的,能显著提高PCG算法的性能,而且对比在单个CPU上使用Python实现的SSOR稀疏近似逆预条件子,提出的GPU加速的SSOR稀疏近似逆预条件子算法平均快将近100 倍.
参考文献:
[1]GOLUB G H, VAN LOAN C F. Matrix computations[M]. Baltimore: The John Hopkins University Press,1989.
[2]王厂文,张有正.正定矩阵和行列式不等式[J].浙江工业大学学报,2006,34(3):351-355.
[3]KAASSCHIETER E F. Preconditioned conjugate gradients for solving singular systems[J]. CAM journal,1988(24):265-275.
[4]龙爱芳.避免二阶导数计算的迭代法[J].浙江工业大学学报,2005,33(5):602-604.
[5]AMENT M, KNITTEL G, WEISKOPF D. A parallel preconditioned conjugate gradient solver for the Poisson problem on a multi-GPU[J]. Parallel distributed and network-based computing,2010(6):583-592.
[6]SAAD Y. Iterative Methods for Sparse Linear Systems[M]. Philadelphia: SIAM,2003.
[7]CHOW E, SAAD Y. Approximate inverse preconditioners via sparse-sparse iterations[ J]. SIAM journal,1998(19):995-1023.
[8]GORTE M J, HUCKLE T. Parallel preconditioning with sparse approximate inverses[J]. SIAM journal,1997(18):838-853.
[9]BELL N, GARLAND M. Efficient sparse matrix-vector multiplication on CUDA[R]. Santa Clara: NVIDIA,2008.
[10]马超,韦刚,裴颂文,等.GPU上稀疏矩阵与矢量乘积运算的一种改进[J].计算机系统应用,2010,19(5):1906-1912.
[11]周洪,樊晓桠,赵丽丽.基于CUDA的稀疏矩阵与矢量乘法的优化[J].计算机测量与控制,2010,18(8):116-120.
[12]DAVIS T A, HU Y. The University of Florida sparse matrix collection [J]. ACM transactions on mathematical software,2011,38(1):1-25.
(责任编辑:陈石平)
Research of the SSOR sparse approximate inverse preconditioner on GPUs
GAO Jiaquan, WANG Zhichao
(College of Computer Science and Technology Engineering, Zhejiang University of Technology, Hangzhou 310023, China)
Abstract:For the SSOR preconditioned conjugate gradient algorithm, the preconditioner equation solving needs the forward/backward substitutions, which greatly prevents parallelizing SSOR PCG algorithms on the GPU platform due to their strong serial processing. Thus, based on the Neumann series approximation, a GPU accelerated SSOR sparse approximate inverse preconditioner is proposed. For GSSORSAI, it preserves the sparse and symmetric positive characteristics of the original coefficient matrix in the linear system, and the preconditioner equation solving only needs a sparse matrix-vector multiplication operation, which avoids the forward/backward substitutions. Experiments results show on the NVIDIA Tesla C2050 GPU, GSSORSAI is generated on average 100 times faster than the implementation by Python on single CPU. Compared to the convergence of the CG algorithm, the PCG algorithm with GSSORSAI has on average 3 times faster convergent rate.
Keywords:SSOR preconditioner; preconditioned conjugate gradient algorithm; sparse approximate inverse; GPU
收稿日期:2015-09-21
基金项目:国家自然科学基金资助项目(61379017)
作者简介:高家全(1972—),男,河南固始人,副教授,博士,研究方向为高性能计算,大数据分析与可视化,智能算法及应用,E-mail:gaojq@zjut.edu.cn.
中图分类号:TP338.6
文献标志码:A
文章编号:1006-4303(2016)02-0140-06

