评分预测问题中个性化推荐模型的研究
孟利民,赵 维,应颂翔
(浙江工业大学 信息工程学院,浙江 杭州 310023)
评分预测问题中个性化推荐模型的研究
孟利民,赵维,应颂翔
(浙江工业大学 信息工程学院,浙江 杭州 310023)
摘要:评分预测问题的主要任务是通过分析用户的历史评分数据集,预测给定用户对新物品的评分,是推荐系统中最热门的问题之一.评分数据表征了用户对物品的明确观点,具有很高的挖掘价值.在对平均值预测模型、基于用户的邻域模型(UserCF)以及基于奇异值分解的模型(SVD)等进行了全面分析和研究的基础上,对各个模型进行了不同程度的改进,最后使用MoiveLens的公开数据集将传统模型和改进后的模型进行对比测试.测试结果表明:改进后的新模型相比传统的推荐模型在推荐结果的精度上有了不同程度的提高.
关键词:推荐模型;邻域模型;矩阵分解;加权融合
人们已经进入信息过载(Information overload)的时代[1].用户面临的烦恼是从纷繁复杂的信息中找到感兴趣的信息;商户需要应对的困难是让信息独具魅力,吸引大批用户的关注.为了决上述矛盾,推荐系统作为一个重要的工具,发挥着巨大的作用[2-4].为了满足提供用户个性化服务的需求,推荐系统在网商平台的商品推荐、新闻媒体推荐、音乐和电影推荐等多个领域内得到广泛应用.个性化推荐起源于上世纪90年代,最早使用个性化推荐技术的有GroupLens[5]和Ringo[6]等系统;2006年在线DVD租赁公司Netflix Prize宣布将一百万美金奖励给能够比其已有推荐算法精确度提高10%的团队(衡量方法是均方差RMSE),大奖在2009年被四个团队共同获得,他们采用了各种技术的混合推荐方法提高了准确度[7].国内的研究起步相对较晚,2009年7月,国内首个个性化推荐系统科研团队北京百分点信息科技有限公司成立;阿里巴巴集团在2015年3月举办了总奖金高达一百万元人民币的主题为穿衣搭配算法和移动电商推荐的“天池大数据竞赛”.
有一部分网站(口碑外卖)利用了进度条评分系统,有一部分网站(天猫,京东)利用五星评分系统,有一部分网站(Youtube)只需要用户选择喜爱还是不喜爱.以上每一种方法都有它们的优势和不足之处,但目标都是希望能够获得用户对物品的明确兴趣.评分预测问题就是分析和利用收集到的评分数据,预测给定用户对给定物品是否感兴趣、感兴趣的程度,以此来决定该物品是否应该推荐给该用户.预测模型的好坏将直接影响预测结果的准确性,准确地将用户感兴趣的物品推荐给用户,会增加用户对网站的满意度和依赖度.当前流行的预测模型中,基于邻域的模型[8]在实际的推荐系统中应用最广,但却面临着如数据稀疏度极大、物品和用户数量的快速增长导致的存储空间和计算量急剧增大等问题.研究人员针对以上问题,在对Netflix的开源数据大量分析的基础上,研究出了基于矩阵分解的一系列模型[9].推荐系统不会使用单一模型进行推荐,在推荐时,往往会结合多个模型,从而给出更加精确的推荐结果.笔者在分析了平均值预测模型、邻域模型及SVD[10]等的基础上,对各个模型进行了不同程度的改进,最后使用MoiveLens的公开数据将传统模型和改进后的模型进行对比测试,结果表明改进后的新模型相比传统的推荐模型在推荐结果的精度上有了不同程度的提高.
1预测模型

(1)
式中Test为测试集合中用户对物品的评分数据集.
1.1平均值预测模型
平均值预测模型主要分为全局平均值模型[2]、用户评分平均值模型[2]及物品评分平均值模型[2]等.
全局平均值模型为
(2)
式中:Train为训练集;u为一给定用户;i为一给定物品;rui为用户u对物品i的评分.下同.
用户评分平均值模型为
(3)
式中N(u)为用户u的评分集合.
物品评分平均值模型为
(4)
式中N(i)为物品i被评分的集合.
1.2基于邻域的预测模型
基于用户的邻域模型[2](UserCF)和基于物品的邻域模型[2](ItemCF)是两种最常见的基于邻域的预测模型.
UserCF预测值定义为
(5)
ItemCF预测值定义为
(6)
1.3基于矩阵分解的预测模型




(7)
为防止过拟合,得到

λ(‖pu‖+‖qi‖)2
(8)
式中:λ(‖pu‖+‖qi‖)2为防止过拟合项;λ为正则化参数.
为使损失函数C(p,q)最小,使用随机梯度下降法[15-18]:第一步分别对p,q的求偏导数,第二步迭代以更新p,q的值.其表达式为

(9)

2模型的改进和融合
2.1改进的基于用户的领域模型
原模型为
(10)
UserCF影响预测准确性的因素:一是在选择K个最相似用户时wuv的选取;二是预测阶段r′的选取.传统的UserCF使用的度量标准是Pearsoncorrelation,其表达式为
(11)
式中I为u和v两用户的评分交集.
wuv的计算结果被用来作为K个最相似用户的选择依据,wuv越大则相似性越大.在日常生活中,每一个领域都有“专家”,这些“专家”在对应的领域投入的时间和精力比普通人多,因此对所在领域发生的事物评价也往往更具有参考价值.从这个角度出发,反过来思考,认为相比其他人投入时间和精力更多的人在该领域的评价更有参考价值.实验使用的数据集是电影的评分数据,可以认为那些评价电影数量较大的人相比于电影评价数量很少的人的评分更具有参考价值,于是把相似度度量标准wuv修改为
(12)
式中:number(v)表示用户v的评分数量;ave代表全部用户评分总数的均值,经过上述修改后,模型加入了“评分物品数量”这一权重因子,即与目标用户评价相同物品的评分相近并且评价过较多物品的用户们将被认为与目标用户更相似.
在进行评分预测时,UserCF中的wuv没有涉及到时间上下文因素,实际上人们的兴趣会随时间发生变化:在很短的间隔时间内,与目标用户相似的用户对相同的物品给出了近似的评价,这样表示该用户与目标用户兴趣更加相似,说明该用户的评价更具参考价值.另外,与目标用户评分物品的交集占各自评分物品数量的比重越大,也能从一定程度反映两者间相似度越高.于是将wuv修改为
(13)
式中:tui,tvi分别为用户u和v对物品i评分时的时间信息;N(u),N(v)分别为用户u,v评分过物品的总数;I为用户u,v评分过的物品交集;μ为兴趣度变化快慢,这与实验对象的选取有关,通过反复实验获得.
用户之间的相似度最直观的体现就是找到两个用户同时评价过的所有物品,计算每个物品的评分差值的绝对值并求和然后做归一化处理,值越小,相似度越高.热门物品和不那么热门的物品是不同的,如果一个物品比较冷门,并且两个用户的评分接近,那么认为这两个用户更相似.于是对热门物品进行“惩罚”,最终得到相似度为
(14)
式中:abs(rui-rvi)为用户u,v对物品i的评分差值的绝对值;s为评分步长由评分规则决定;l为正整数,需要反复实验获得;l×s作为一个分界线,超过该分界线,则两用户对同一物品意见差别极大;N(i),N(u),N(v)分别代表物品i被评分的数量,用户u,v评分物品的数量.将这一模型称为D_UserCF.
2.2BiasSVD和T-SVD
1.3节提到的LFM,其评分预测公式为
(15)
实际上,每个评分系统都有与用户不相关同也和物品不相关的特性,用户也有与物品不相关的特性,物品也有与用户不相关的特性.把评分预测公式修改为
(16)
该模型称为BiasSVD,其中μ代表全局评分均值,bi代表物品i评分偏置项,代表物品在被评分时与用户不相关的特性,bu代表用户u的评分偏置项,代表用户在评分时与物品不相关的特性.加入偏置项后,损失函数为
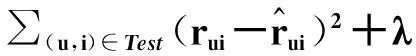
‖qi‖2+‖bi‖2+‖bu‖2)
(17)
最小化损失函数为
(18)
在原有基础上加入时间信息,进而得到损失函数为
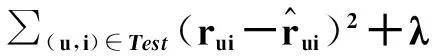
‖qi‖2+‖btui‖2)
(19)
最小化损失函数为
(20)
2.3模型加权融合
(21)
式中γi为第i个预测器的权重.
实验中,分别选取平均值预测模型、UserCF和SVD中评分精确度最接近的两个模型进行加权融合,为降低预测误差,使用最小二乘法计算得到γ0,γ1,γ2的值.
误差平方和为

(22)
根据极值存在的必要条件有

(23)

3实验
实验设备:阿里云服务器,操作系统为CentOS release 6.6,CPU型号:Intel(R) Xeon(R) CPU E5-2630 0@2.30 GHz 4核,内存大小:4.00 GB.
3.1实验说明
实验中使用的数据来自MoiveLens,内容包含用户7 000多人,影片15 000多部,评分数据90多万条.MoiveLens规定任意用户需要对大于等于15部的电影进行过评分.把数据集依据时间戳降序排列后分为训练集X和测试集Y,其中X为全集的90%,Y为全集的10%,再将X用上述方式分为X1和X2,在X1上训练不同的预测器,然后在X2上测试,同时获得融合系数,接下来把加权融合后的模型在Y上进行测试,即可获得最后的预测值.为了方便描述,把融合后的均值模型称为UI-average;把选择k个近邻用户过程中,计算相似度时加了评价数量权重的UserCF算法称为W_UserCF,把预测过程中加入了时间信息的算法称为T_UserCF,融合得到的模型称为WT_UserCF,再对WT_UserCF和D_UserCF进行加权平均,得到WTD_UserCF;T-SVD和Bias-SVD融合后得到的模型称为TB-SVD.
UserCF中近邻用户数量k是一个重要参数,在保证准确度的情况下,取k=25,对于改进的模型T_UserCF还有一个用户兴趣度变化快慢的参数μ,通过交叉测试,取μ=10-7.SVD模型中有3个重要参数,隐特征向量维数f,正则化参数λ和学习速率α,在保证正确的情况下取f=100,α的选取会影响迭代次数,这里选取α=0.025,迭代次数约为30次结束,通过交叉试验得到λ=0.04.
3.2实验结果与分析
从表1~3的实验结果可以看出:对传统算法的每一次改进,算法在预测准确度上有了不同程度的提高,通过加权融合所得到的预测模型在准确度上超越了其他模型.

表1 均值模型

表2 基于用户的领域模型

表3 基于矩阵分解的SVD模型
4结论
首先对平均值预测模型、UserCF及SVD等进行了全面的分析和研究,在此基础上对各模型进行修改和融合.对均值模型进行了加权融合,得到了UI-average,相比Item-average精确到提升了0.072 4,对基于用户的邻域模型进行了相似度的修改,最后得到的融合模型相比原模型精确度到提升了0.047 3,通过对Bias-SVD和T-SVD融合获得的TB-SVD,相比原模型精确度也有一定提升.实验结果表明:改进后的新模型相比原来的模型在推荐结果上都更加接近于真实值.
参考文献:
[1]YANG C C, CHEN H, HONG K. Visualization of large category map for internet browsing[J]. Decision support systems,2003,35(2):89-102.
[2]项亮.推荐系统实践[M].北京:人民邮电出版社,2012.
[3]冷亚军,陆青,梁昌勇.协同过滤推荐技术综述[J].模式识别与人工智能,2014,27(8):720-734.
[4]许海玲,吴潇,李晓东,等.互联网推荐系统比较研究[J].软件学报,2009,20(2):350-362.
[5]RESNICK P, IACOVOU N, SUCHAK M, et al. GroupLens: an open architecture for collaborative filtering of netnews[C]// In proceedings of the 1994 Acm Conference on Computer Supported Cooperative Work. Chapel Hill: Acm,1994:175-186.
[6]SHARDANAND U, MAES P. Social information filtering: algorithms for automating “word of mouth”[C]// Proceedings of Acm CHI’95 Conference on Human Factors in Computing Systems. Denver: Acm,1995:210-217.
[7]ZHOU Y, WILKINSON D, SCHREIBER R, et al. Large-scale parallel collaborative filtering for the netflix prize[C]//Algorithmic Aspects in Information and Management. Berlin:Springer,2008:337-348.
[8]HERLOCKER J L, KONSTAN J A, Terveen L G, et al. Evaluating collaborative filtering recommender systems[J]. Acm transactions on information systems,2004,22(1):5-53.
[9]BENNETT J, LANNING S, NETFLIX N, et al. The netflix prize[EB/OL]. [2015-09-15]. https://www.cs.uic.edu/~liub/KDD-cup-2007/NetflixPrize-description.pdf.
[10]GOLUB G H, REINSCH C. Singular value decomposition and least squares solutions[M]. Berlin: Linear AlgebraSpringer,1971:134-151.
[11]XIANG L, YANG Q. Time-dependent models in collaborative filtering based recommender system[J]. Web intelligence & intelligent agent technologies,2009(1):450-457.
[12]KOREN Y, BELL R, VOLINSKY C. Matrix factorization techniques for recommender systems[J]. Computer,2009,42(8):30-37.
[13]KOREN Y. Collaborative filtering with temporal dynamics[J]. Communications of the Acm,2010,53(4):89-97.
[14]KOREN Y. Factor in the neighbors: scalable and accurate collaborative filtering[J]. Acm transactions on knowledge discovery from data,2010,4(1):1-24.
[15]哈林顿.机器学习实战[M].北京:人民邮电出版社,2013.
[16]肖刚,吴利群,张元鸣,等.一种基于协作频度聚类的Web服务信任评估方法[J].浙江工业大学学报,2014,42(4):393-399.
[17]刘端阳,王良芳.基于语义词典和词汇链的关键词提取算法[J].浙江工业大学学报,2013,41(5):545-551.
[18]孟利民,包轶名.基于局部特征的图像插值算法在B/S视频监控中的应用[J].浙江工业大学学报,2015,43(2):217-221.
(责任编辑:陈石平)
Research on the personalized recommendation model in rating prediction
MENG Limin, ZHAO Wei, YING Songxiang
(College of Information Engineering, Zhejiang University of Technology, Hangzhou 310023, China)
Abstract:Rating prediction is one of the hottest issues in the recommendation system. Its main task is to predict a user’s rating for a new item based on the analysis of user’s history rating data. The rating data reveal the user’s view on items clearly and it will be of high mining value. The average prediction model, the neighborhood-based user model and the singular value decomposition-based model are studied and improved with certain degrees. Based on the MoiveLens’s public data set, the traditional model and the improved model are compared. The test results show that the improved model is better than the traditional model in prediction accuracy.
Keywords:recommendation model; neighborhood model; matrix factorization; weighted fusion
收稿日期:2015-10-20
基金项目:国家自然科学基金资助项目(61372087)
作者简介:孟利民(1963—),女,浙江金华人,教授,研究方向为无线通信与网络多媒体数字通信,E-mail:mlm@zjut.edu.cn.
中图分类号:TP391
文献标志码:A
文章编号:1006-4303(2016)02-0119-05

