恢复部分支集已知的稀疏信号
王会敏
(绍兴文理学院 数学系,浙江 绍兴312000)
恢复部分支集已知的稀疏信号
王会敏
(绍兴文理学院数学系,浙江绍兴312000)
摘要:讨论如何从少量线性测量中恢复部分支集信息已知的稀疏信号的问题.所用方法是凸优化方法,所用范数为关于已知支集的余集上的l1范数.文章讨论了支集信息不完全准确的情形,给出了保证信号稳定恢复的限制等距常数界.
关键词:压缩感知;l1范数最小化;限制等距常数
引言
压缩感知是一个最近出现的热门领域,主要目标是从少量的线性测量中恢复稀疏信号.因为在很多应用问题中,要恢复的信号都是稀疏的或者渐进稀疏的,压缩感知的潜在应用前景非常广.

min‖x‖0,s.t.y=Φx
(1)
恢复x.

min‖x‖1,s.t.y=Φx
(2)
Candes,Romberg和Tao[2]表明通过选择合适的测量矩阵,只要测量次数m>Cklog(n/k),则通过求解l1范数最小化问题可以稳定恢复k-稀疏信号.注意到这里讨论的恢复方法并没有用到信号的一些先验信息.
在实际的应用中,要恢复的稀疏信号往往有一些先验信息,比如信号的部分支集已知,或者信号的最大分量的估计等可以用来改善信号恢复的表现.比如,视频信号往往会表现出相邻框架上的相关性.考虑一个压缩信号x∈Rn,如果x表示一个图像的离散cosine变换或者小波变换的稀疏化,则x对应于低频子带的分量最可能是非零的,并且负荷了信号的大部分能量.这样的情形下,当x被压缩采样时,在恢复算法中考虑这些信息,是有助于恢复的.例如,Garcis-Frias和 Esnaola[3]表明如果一个信号是一个随机过程的实现,统计先验信息有助于改进信号恢复的质量.Elad和Aharon[4]讨论了图像的稀疏和冗余表示,定义了全局信号的先验信息,强迫导致片段上的稀疏性来发展一种图像去噪的方法.Weizman等讨论了采用迭代加权方法,利用先验信息恢复MRI图像的问题[5].
本文考虑部分支集信息已知的信号恢复,已知的支集信息不一定完全准确,可能有一定误差.
1数学模型
令x0∈Rn是要恢复的信号,T0∈suppx0.假定部分支集估计T⊂{1,...,n},则一个可能的构造方法是
x*=argmin‖x‖1,w,s.t.y=Φx
(3)

min‖x‖1,w,s.t.‖y-Φx‖ε
(4)
C.Miosso等在[6]中提出了一个基于迭代加权最小二乘算法的加权策略来处理已知支集的先验信息.数值结果表明先验信息的使用会使得需要的测量次数下降.Vaswani等在[7]中研究了迭代重构稀疏信号序列的问题,其中将上一次试验得到的支集估计作为下一次的已知支集信息.他们得到了准确重构的充分条件.本文考虑了得到的支集信息不准确的情形,并用限制等距常数刻划了稳定恢复的条件.
2限制等距常数
下面介绍限制等距常数的概念.
定义1令Φ∈Rm×n是给定矩阵.对满足1km的任意正整数k,定义Φ的k阶限制等距常数是满足下列条件的最小的正数δk∈(0,1),

对所有k-稀疏信号x∈Rn成立.显然,当kk'时,δkδk',.
下面介绍一个限制正则常数的概念.
定义2令X,X'∈Rm×n,满足R(X)r,R(X')r',并且〈X,X'〉=0,r,r'-阶限制正则常数θr,r'是满足下列条件的最小正数
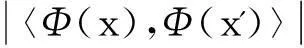
在[8]中,研究者提供了下面的不等式
θr,r'θr1,r1',如果rr',r1r1',
θr,r'δr+r'θr1,r1'+max(δr,δr')
3主要结果及证明



则(*)式的解x*满足
‖x*-x0‖2
对于任意正整数r和ri,1il,有

特别,对于任意a≥1和正整数r和r',使ar'是正整数,则
θr,ar'.

δ2k
令x*=x0+h是(*)式的解,则应用与[9]中类似的表示,可以得到
‖hc‖1
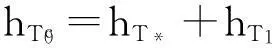

分解hi=hi1+hi2,i=1,...,l,这里hi1是hi中前b-a个最大系数的分量构成的向量.有
‖h1‖2,
‖h2‖2,...,‖hi‖2,...,则

注意到x*和x都是可行解,因此有‖Φh‖2ε.根据限制等距性质有
〈Φh,Φ(h0+h*)〉
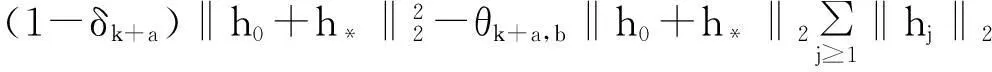


〈Φh,Φ(h0+h*)〉

另一方面,由于
〈Φh,Φ(h0+h*)〉‖Φh‖2‖Φ(h0+h*)‖2,


有
‖h‖2).
证毕.
参考文献:
[1]E J Candes. Compressed sampling[J].In International Congress of Mathematics,2006, 3:1433-1452.
[2]E J Candes,J Romberg,T Tao.Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J].IEEE.Trans.Inform.Theory,2006,52(2):489-509.
[3]J G Frias,I Esnaola.Exploiting prior knowledge in the recovery of signals from noisy random projections[J].In Data Compression Conference, 2007:333-342.
[4]M Elad,M Aharon.Image denoising via sparse and redundant representations over learned dictionaries[J].IEEE.Trans.Image.Process,2006,15:3726-3745.
[5]L Weizman,Y Eldar,D Bashat.Compressed sensing for longitudinal MRI: An adaptive-weighted approach[J].Medical Physics, 2015, 42(9):5195-5208.
[6]C J Miosso,R von Barries,M Argaez,et al.Compressive sensing reconstruction with prior information by iteratively reweighted least squares[J].IEEE.Trans.Sig.Proc,2010,57(6):2424-2431.
[7]N Vaswani.Least squares CS-residual(LS-CS):Compressive sensing on Least squares residual[J].IEEE.Trans.Sig.Proc,2010:58.
[8]T Tony Cai,Lie Wang,Guangwu Xu.Shifting inequality and recovery of sparse signals[J].IEEE Transactions on signal processing,2010,58(3):1300-1308.
[9]M P Friedlander,H Mansour,R Saab, et al.Recovering compressively sampled signals using partial support information[J].IEEE.Trans.Info.Theory,2012,58(2):1122-1134.
(责任编辑鲁越青)
Recovering Sparse Signals with Partial Support Information
Wang Huimin
(Department of Mathematics, Shaoxing University, Shaoxing, Zhejiang 312000)
Abstract:In this paper, we consider recovering sparse signals with prior support information. We assume that the positions of some nonzero elements have been known. We propose a weighted optimized approach and derive the sufficient condition to guarantee a successful recovery.
Key words:matrix completion; nuclear norm minimization; singular value decomposition
收稿日期:2016-03-10基金项目:浙江省自然科学基金青年基金项目(LQ14A010005),浙江省教育厅科研项目(Y201328557).
作者简介:王会敏(1980-),女, 河南安阳人,博士,讲师,主要研究方向:压缩感知与低秩矩阵恢复.
doi:10.16169/j.issn.1008-293x.k.2016.07.07
中图分类号:C25
文献标志码:A
文章编号:1008-293X(2016)07-0035-04

