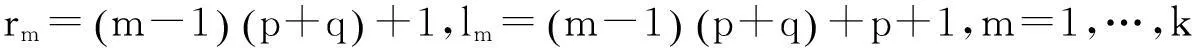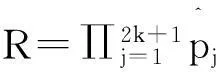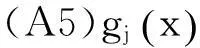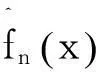NA样本下含附加信息时概率密度函数的估计

邓　裕　秦永松　董　凯

(浙江师范大学　数理与信息工程学院，浙江　金华321004)



NA样本下含附加信息时概率密度函数的估计

邓裕秦永松董凯

(浙江师范大学数理与信息工程学院，浙江金华321004)

摘要：利用分块方法证明了NA样本下含附加信息时概率密度估计的渐进分布为正态分布.

关键词：NA样本；概率密度估计；分块经验似然；渐近分布

1引言

首先给出NA样本和核密度估计的定义.

其中f和g是任何两个使得协方差存在的且对每个变元均非降(或对每个变元均非升)的函数,则称该序列为负相协(NA)随机变量序列.

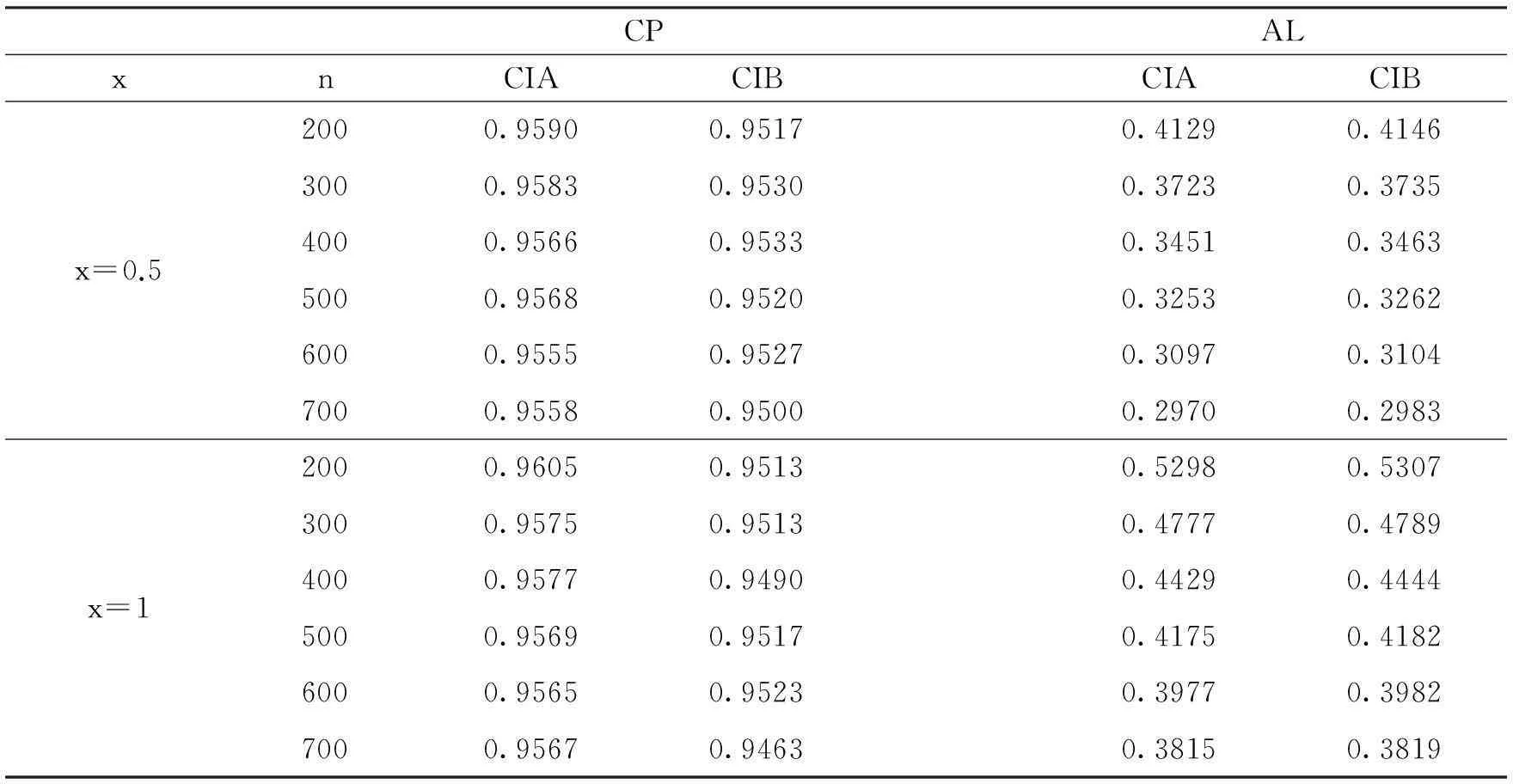
其中K(·)为核函数,0

在独立样本情形时,Rosenblatt[2],Pazren[3],Rao[4]以及Silverman[5]等对密度核估计做了比较深入的研究,也得到了比较好的结果.Roussas[6]研究了在不含附加信息是NA序列下概率密度函数的估计,并证明了其渐进分布为正态分布.Chen[7]在1999年给出了在独立样本情况下含附加信息时概率密度函数的估计,但还尚未见在NA样本序列的情况下含附加信息时概率密度函数的估计.本文将在NA序列样本下讨论含附加信息的概率密度函数的估计.

2假设条件及主要结果

(2.1)

定义如下经验似然函数

(2.2)

其中

为了获得在含附加信息时的核密度估计的渐进性质,我们需要如下假设条件:

(A1)1)随机变量序列为强平稳序列,是该序列对于Lebesgue测度的一维边缘密度函数.

3)随机变量X1,Xj+1的联合概率密度函数f1,j并且满足条件

4)f的导数f'存在并且有界;

(A2)～核函数K是一个有界的概率密度函数,并且满足

∫RuK(u)du=0,∫Ru2K(u)du<,<.

注1条件(A1)-(A4)在文献[6]中给出用于研究NA样本情形下不含附加信息的概率密度函数的估计.

定理2.1

假设条件(A1)-(A5)满足,则有

3模拟结果

CIB在置信水平为1-α的NACI为

表1

CPALxnCIACIBCIACIBx=0.52000.95900.95170.41290.41463000.95830.95300.37230.37354000.95660.95330.34510.34635000.95680.95200.32530.32626000.95550.95270.30970.31047000.95580.95000.29700.2983x=12000.96050.95130.52980.53073000.95750.95130.47770.47894000.95770.94900.44290.44445000.95690.95170.41750.41826000.95650.95230.39770.39827000.95670.94630.38150.3819

由上述模拟结果可知,随着n的增加,两种模型的CP趋于置信水平,置信区间的AL逐渐变小.并且看到CIA比CIB有更好的CP及更短的AL.

4引理

引理4.1[8]

引理4.2[9]

设条件(A1)-(A3)满足,则

(4.3)

引理4.3[6]

当条件A(1)-A(4)都满足时,

引理4.4

当条件(A1),(A4),(A5)～都满足时，则

(4.4)

为证明引理4.4,首先证明

(4.5)

由文献[9]中式(4.7)的证明知

对于其他项,计算以下式子

并利用文献[10]的引理1.1和引理1.2,可得

用类似的方法可证

结合以上结果,式(4.5)得证.

现证

(4.6)

其中

为证式(4.6)首先证明

(4.7)

为此先证对于任意的l∈Rr+1满足lτl=1,有

(4.8)

只要证明

(4.9)

(4.10)

(4.11)

(4.12)

类似可证

(4.13)

通过式(4.12)以及(4.13)容易得到式(4.9)和(4.10)

(4.14)

从而有

(4.15)

由式(4.6)和强平稳性,利用文献[6]中引理3.3的类似证明方法可得

是收敛的.设bs是Rr+1中的第s个标准坐标向量,1sr+1.取l=bs,bt以及s,tr+1,s≠t,当q→时,得

(4.16)

进而,

(4.17)

结合式(4.15)和(4.17)有

这样式(4.11)得证.综上,式(4.8)证.

下面再证

(4.18)

令

其中

(4.19)

通过引理1,式(4.5)以及条件A(3),A(4)可得

类似可以证明

以及

这样,式(4.18)得证.

通过式(4.8)和(4.18)可得

(4.20)

设bs是Rr+1中的第s个标准坐标向量,1sr+1.设的第(s,t)个元素为Sqst.设l=bs,bt以及s,tr+1,s≠t,再次利用式(4.20)便可得到,s≠t,式(4.6)得证,从而得到.引理得证.

引理4.5

下证

(4.21)

即证

(4.22)

其中lτl=1.由条件A(4)可得

则式(4.22)得证,从而式(4.21)成立.引理得证.

5定理的证明

定理2.1的证明

定理得证.

参考文献:

[1]Esary J D, Proschan F, Walkup D W. Association of random variables with application[J]. Ann. Math. Statist.,1967,38(5):1466-1474.

[2]Rosenblatt M, Remark on Nonparametric Estimates of a Density Function[J]. Ann. Math.Statist.,1956(27):832-837.

[3]Parzen E. On estimation of a probability density function and mode[J]. Ann. Math. Statist.,1962(33):1065-1076.

[4]Prakasa Rao B L S. Nonparametric function estimation[M].New York： Academic Press,1983.

[5]Sliver B W. Density Estimation for Statistics and Bata Analysis[M].London: Chapman and Hall,1986.

[6]Roussas G G. Asymptotic normality of the kernel estimate of a probability density function under association[J]. Statistics. and Prob. Lett,2000(50):1-12.

[7]Chen S X. Empirical likelihood-based kernel density estimation[J]. Austral. J. Statist,1997,39(1):47-56.

[8]Yang S C. Uniformly asymptotic normality of the regression weighted estimator for negatively associated samples[J]. Statist Probab Lett,2003(62):101-110.

[9]Qin Y S, Lei Q Z. Quantile Estimation in the Presence of Auxiliary Information under Negatively Associated Samples[J]. Statistics-Theory and Methods,2011(40):4289-4307.

[10]Zhang L X. The weak convergence for functions of negatively associated random variables[J]. Journal of Multivariate Analysis,2001(3):1325-1332.

(责任编辑鲁越青)

Estimator of Probability Density Functions inPresence of Auxiliary Information under Negatively Associated Samples

DengYu Qin Yongsong Dong Kai

(School of Mathematics, Physics and Information Engineering, Zhejiang Normal University, Jinhua, Zhejiang 321004)

Abstract：By using the block-wise technique, this paper demonstrates that the asymptotic distribution of the probability density functions including extra messages is of normal distribution under negatively associated samples.

Key words：negatively associated sample; probability density estimation; block-empirical likelihood; asymptotic distribution.

收稿日期：2015-10-26基金项目：国家自然科学基金(11271088，11361011)

作者简介：邓裕(1991-)，男，浙江杭州人，在读研究生，研究方向：概率论与数理统计

doi：10.16169/j.issn.1008-293x.k.2016.07.08

中图分类号：O212

文献标志码：A

文章编号：1008-293X(2016)07-0039-09