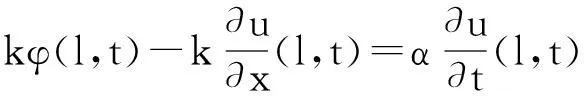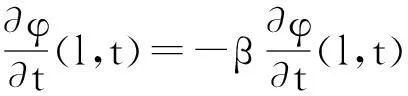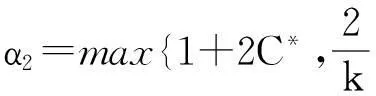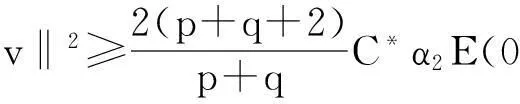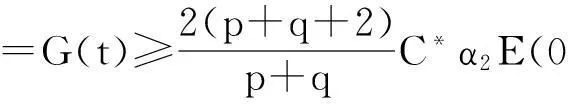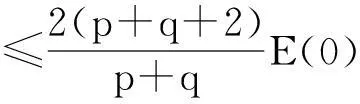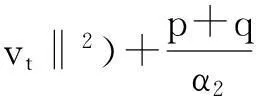半线性Timoshenko系统解的爆破性

张桂霞

(三门峡市教师进修学校，河南 三门峡 472000)



半线性Timoshenko系统解的爆破性

张桂霞

(三门峡市教师进修学校，河南 三门峡 472000)

[摘要]研究了一类半线性Timoshenko系统初边值问题解的爆破性.利用凸性方法分三种情况给出了具任意初始能量和适当的初始条件下，Timoshenko系统初边值问题解的爆破性条件.

[关键词]Timoshenko系统；初边值问题；凸性方法；爆破性

1引言

本文研究如下一类半线性Timoshenko系统初边值问题解的爆破性

utt-uxx+k(u+vx)=(p+1)|v|q+1|u|p-1u，

00，

(1.1)

vtt-k(u+vx)x=(q+1)|u|p+1|v|q-1v，

00，

(1.2)

u(0，t)=v(0，t)=u(1，t)=v(1，t)=0，

t>0，

(1.3)

u(x，0)=u0(x)，ut(x，0)=u1(x)，

0

(1.4)

v(x，0)=v0(x)，vt(x，0)=v1(x)，

0

(1.5)

其中k>0为正常数，p，q>1 ，初始值u0，u1，v0，v1是给定的.当方程(1.1)，(1.2)的右边非线性项是零时，即

utt-uxx+k(u+vx)=0，

(1.6)

vtt-k(u+vx)x=0

(1.7)

它是著名的Timoshenko梁方程[1]，这里其中，t表示时间变量，x表示位置变量，梁的长度是1，v表示梁的横向位移，u是旋转角.由于它的广泛应用，在过去的几十年中，Timoshenko梁方程引起了人们的极大兴趣.方程(1.6)，(1.7)在各种边界条件下，其解的存在性和渐近性已有许多好的结果， 例如，Kim和Renardy[2]用乘子技巧在边界条件

下得到了问题的能量指数衰减.Raposo等[3]则用半群方法在具有线性摩擦阻尼项和齐次Dirichlet边界条件下得到了问题的能量指数衰减估计.Soufyane和Wehbe[4]利用局部分布反馈给出问题的一致稳定的充要条件.还有许多文献研究了具有记忆项等情况，这里不再一一列举.下面我们仅提一下对半线性Timoshenko系统的研究情况.Parente等[5]研究了如下问题

utt-uxx+k(u+vx)+f(u)=0，

(1.8)

vtt-k(u+vx)x+g(v)=0

(1.9)

vtt-k(u+vx)x=g(v)，

解的衰减估计和吸收集的估计，其中外力项f(u)，g(v)满足局部Lipschitz连续.Messaoudi和Soufyane[9，10]在高维情形边界记忆项非线性Timoshenko系统的一般衰减估计

然而，据作者所知，很少有人研究带有源项的Timoshenko系统.最近，Pei等人[11， 12]利用位势井理论研究了ReissnerMindlin-Timoshenko板系统解的整体适定性和长时间行为，他们主要聚焦于非线性阻尼项和源项的相互作用问题.

本文将研究带有源项的Timoshenko系统整体解的不存在性.虽然我们用的是经典的凸性方法[13]，但本文也遇到了出现范数‖u+vx‖如何处理的困难，为此，我们给出了一个等价不等式.另外，我们避免引入位势井而证明了对任意初始能量解的爆破问题.我们分初始能量小于、等于和大于三种情况对初始值要求不同的条件证明爆破结果.特别是，对初始能量大于零的情况，我们的方法不同于已有文献[14，15].

第二节中将会给出一些概念和准备，第三节中将给出解爆破的证明.

2准备知识

‖u‖s≤C*‖ux‖.

(2.1)

E(t)=E(0)，

(2.2)

其中

(2.3)

(2.4)

再引入如下泛函

(2.5)

为以后处理‖u+vx‖的需要，我们给出如下引理.

α1(‖ux‖2+k‖u+vx‖2)≤‖ux‖2+‖vx‖2≤α2(‖ux‖2+k‖u+vx‖2).

(2.6)

证明注意到

|vx|2=|u+vx-u|2≤2(|u+vx|2+|u|2)，

利用(2.1)得

‖ux‖2+‖vx‖2

≤‖ux‖2+2‖u+vx‖2+2‖u‖2

≤(1+2C*)‖ux‖2+2‖u+vx‖2

‖ux‖2+k‖u+vx‖2

≤‖ux‖2+2k‖vx‖2+2k‖u‖2

≤(1+2kC*)‖ux‖2+2k‖vx‖2

≤α1-1(‖ux‖2+‖vx‖2)

其中α1-1=max{1+2kC*，2k}，从而得结论.

3解的爆破

下面分E(0)<0、E(0)=0和E(0)>0三种情况讨论解的爆破条件.对E(0)≤0我们用经典的凸性方法[13]，而对E(0)>0，我们的方法不同于已有文献[13，14，15].

(u0，u1)+(v0，v1)>0，

证明首先讨论E(0)<0的情况，构造辅助函数

φ(t)=‖u‖2+‖v‖2+b(t+T2)2，

(3.1)

其中b和T2是待定的正常数.易得

φ′(t)=2(u，ut)+2(v，vt)+2b(t+T2)，

(3.2)

φ″(t)=2‖ut‖2+2‖vt‖2+2(u，utt)+2(v，vtt)+2b

=2‖ut‖2+2‖vt‖2-2I(u，v)+2b.

(3.3)

再利用E(t)的表示式知

φ″(t)=(p+q+4)(‖ut‖2+‖vt‖2)+(p+q)(‖ux‖2+k‖u+vx‖2)-2(p+q+2)E(t)+2b.

因为E(0)<0，取常数b满足0

-2(p+q+2)E(t)+2b>(p+q+4)b，

这意味着

φ″(t)≥(p+q+4)(‖ut‖2+‖vt‖2+b).

显然，有

φ″(t)≥0，t∈[0，T1).

(3.4)

进一步，可取充分大的T2和适当的b使

φ′(0)=2(u0，u1)+2(v0，v1)+2bT2>0，

于是对每一t∈[0，T1)有φ(t)>0和φ′(t)>0，从而t∈[0，T1)有φ(t)和φ′(t)在t∈[0，T1)上严格增.由Cauchy-Schwartz不等式，易得

(3.6)

于是对每一t∈[0，T1)

(3.7)

下面讨论的E(0)=0且(u0，u1)+(v0，v1)>0情况.这时，定义

G(t)=‖u‖2+‖v‖2

直接计算知

G′(t)=2(u，ut)+2(v，vt)，

(3.8)

G″(t)=2‖ut‖2+2‖vt‖2-2I(u，v).

(3.9)

易知，

由(3.9)则

G″(t)>0，

(3.10)

注意到G′(0)=2(u0，u1)+2(v0，v1)>0则有

G′(t)>0，

(3.11)

于是由(3.10)，(3.11)知，G(t)和G′(t)在t∈[0，T1)上严格增.进一步，

G″(t)=(p+q+4)(‖ut‖2+‖vt‖2)+(p+q)(‖ux‖2+k‖u+vx‖2)-2(p+q+2)E(0)

注意到E(0)=0知

G″(t)≥(p+q+4)(‖ut‖2+‖vt‖2)，

因G(t)>0，由Cauchy-Schwartz不等式，易得

余下类似E(0)<0的情况得结论.

E(0)>0，

(3.12)

I(u0，v0)<0，

(3.13)

(u0，u1)+(v0，v1)>0，

(3.14)

(3.15)

证明分两步证明.首先证明对t∈[0，T1)

I(u(t)，v(t))<0，

(3.16)

(3.17)

用反证法证明(3.16). 假设(3.16)对某一t∈[0，T1)不成立，即存在T>0使得

T=min{t∈[0，T1)，I(u(t)，v(t))≥0}，

(3.18)

则由I(u(t)，v(t))关于t的连续性，

I(u(T)，v(T))=0.

(3.19)

令G(t)=‖u‖2+‖v‖2有

G′(t)=2(u，ut)+2(v，vt)，

(3.20)

G″(t)=2‖ut‖2+2‖vt‖2-2I(u，v).

(3.21)

注意到由(3.18)的定义知对每一t∈[0，T)

I(t)=I(u(t)，v(t))<0，

(3.22)

可知在t∈[0，T)上有G″(t)>0.再由(3.13)知，对t∈[0，T)上有G′(t)>0.从而有在t∈[0，T)上在G(t)和G′(t)严格增.再由(3.15) 对t∈[0，T)则

‖u‖2+‖v‖2

(3.23)

因u(t)，v(t)关于t连续，从(3.18)得

(3.24)

另一方面，由(2.2)和E(t)的定义

<2E(0)，

(3.25)

由(3.19)知

此式结合(3.25)得

‖ux(T)‖2+k‖(u+vx)(T)‖2

(3.26)

由(3.26)结合(2.2)知

G(T)=‖u(T)‖2+‖v(T)‖2

≤C*(‖ux(T)‖2+‖vx(T)‖2)

≤C*α2(‖ux(T)‖2+k‖(u+vx)(T)‖2)

(3.27)

显然，(3.24)和(3.27)矛盾，于是得结论(3.16).由上述讨论可见，若I(u(t)，v(t))<0和(3.14)成立，G(t)在t∈[0，T)上严格增，由(3.16)易知(3.17)成立.

最后证明爆破性.简单的计算知

(3.28)

由(3.28)及Cauchy-Schwartz不等式得

余下类似E(0)<0的情况得结论.

[参考文献]

[1]Timoshenko S. On the correction for shear of the differential equation for transverse vibrations of prismatic bars[J]. Philosophical Magazine， 41(1921)， 744 - 746.

[2]Kim J.U.，Renardy Y. Boundary control of the Timoshenko beam[J]. SIAM J. Control Optim.， 25(6)(1987):1417-1429.

[3]Raposo C.A.， Ferreira J.， Santos M.L.， Castro N.N.O. Exponential stability for the Timoshenko system with two weak dampings[J]. Appl. Math. Lett.， 2005， 18: 535-541.

[4]Soufyane A.， Wehbe A. Uniform stabilization for the Timoshenko beam by a locally distributed damping[J]. Electron.J.Differential Equations， 29(2003): 1-14.

[5]Parente A.， Miranda M.M.， Jutuc L.P.S.G. On local solution for a nonlinear Timoshenko system[C]. Proccedings of the 55° SBA， UFU， Uberlandia-MG-Brazil， 2002:167-179.

[6]Araruna F.D.， Borges J.E.S. Existence and boundary stabilization of the semilinear Mindlin-Timoshenko system[J]. EJQTDE， 34(2008):1-27.

[7]Chueshov I. Lasiecka I. Global attractors for Mindlin-Timoshenko plates and for their Kirchhoff limits[J]. Milan J.Math.，74(2006):117-138.

[8]Gorgi C.， Vegni F.M. Uniform energy estimates for a semilinear evolution equation of the Mindlin-Timoshenko beam with memory[J]， Mathematical and Computer Modelling， 39 (2004)， 1005-1021.

[9]Messaoudi S. A.， Soufyane A. Boundary stabilization of a nonlinear system of Timoshenko type[J]. Nonlinear Analysis， 67 (2007)， 2107 - 2112.

[10]Soufyane A.， Afilal M.， Aouam T. General decay of solutions of a nonlinear Timoshenko system with a boundary control of memory type[J]. Differential and Integral Equations， 22(2009)， 1125 - 1139.

[11]Pei P.， Rammaha M.A.， Toundykov D. Local and global well-posedness of semilinear Reissner-Mindlin-Timoshenko plate equations[J]. Nonlinear Analysis， 105 (2014)， 62 - 85.

[12]Pei P.， Rammaha M.A.， Toundykov D. Global well-posedness and stability of semilinear Mindlin-Timoshenko systems[J]. J. Math. Anal. Appl.， 418 (2014)， 535 - 568.

[13]Levine H A. Instability and nonexistence of global solutions to nonlinear wave equations of the form [J]. Trans. Amer .Math. Soc. 192(1974)， 1-21.

[14]Messaoudi S A，Said-Houari B， Global nonexistence of positive initial energy solutions of a system of nonlinear viscoelastic wave equation with damping and source terms[J]，J. Math Anal Appl，365(2010)，277-287.

[15]Ma J， Mu C L， Zeng R， A blow-up result for viscoelastic equations with arbitrary positive initial energy[J]， Boundary Value Problems，6(2011)，1-10.

[16]Wloka J. Partial Differential Equation[M].Cambridge University Press， London， 1987.

[责任编辑：张怀涛]

Blow up for a semilinear Timoshenko system

ZHANG Gui-xia

(Sanmenxia Teachers Training School， Sanmenxia 472000，China)

Abstract:This paper discusses the initial boundary value problem of the semilinear Timoshenko system. By the convexity method，based on three cases，some blow-up results for the solution to the Timoshenko system is obtained under arbitrary initial energy and appropriate initial datum.

Key words:Timoshenko system; convexity method; initial boundary value problem; blowup

[收稿日期]2015-12-05

[基金项目]河南省基础与前沿研究项目(1323004100360)

[作者简介]张桂霞(1963-)， 女，高级讲师，主要从事微分方程方向的研究。

[中图分类号]O172.27

[文献标识码]A

[文章编号]1671-5330(2016)02-0007-05