实变函数教学中的铺垫教学法

冯　颖

(西南交通大学数学学院，成都611756)



实变函数教学中的铺垫教学法

冯颖

(西南交通大学数学学院，成都611756)

[摘要]讨论在实变函数课程教学中进行铺垫教学的重要性.结合教学案例，从教学引入、概念教学、定理结论教学、提出问题、拓展延伸等方面探讨了铺垫教学法在实变函数教学中的应用.

[关键词]实变函数； 教学方法； 铺垫教学

1引言

实变函数课程是本科数学类各专业的一门必修基础课，一般安排在数学分析课程后，是一门承上启下的课程，其主要内容是勒贝格测度论和积分理论[1,2].掌握现代的积分论知识，提高学生的抽象分析能力，培养学生的分析素养是该课程的主要教学目的.在教学实践中，实变函数课程本身高度的理论性和抽象性使多数学生对这门课程的学习存在畏难情绪，学习效果不理想.如何调动学生的主观能动性，激发其学习兴趣与潜能，帮助学生“轻松”掌握课程的主要思想和内容是课程教学中亟待解决的问题.

笔者在教学实践中发现，适时的、精心设计的“教学铺垫”能有效改善教学效果，增强学生的学习信心，调动学生的学习热情.所谓“铺垫”指的是事物发展过程中的前期准备工作.铺垫式教学法可以拉近学生和教学的距离，为课程的展开提供充分的准备和酝酿.教学引入性铺垫，为新知识的学习揭开神秘的面纱，让学生明白所学内容产生的背景.概念教学性铺垫，承上启下，自然过渡，使新旧知识融为一体.定理结论铺垫，则化解难点，为学习开山辟路.问题导入性铺垫，设疑启发，调动学习的积极性.延伸拓展性铺垫，扩展学生的视野，让学生了解知识的发展和应用.

本文结合具体的教学实践和体会，以案例的形式探讨铺垫教学法在实变函数教学中的应用.

2铺垫教学法实践

2.1教学引入性铺垫，揭示数学的精神

教学引入性铺垫，可视为每节课的“引言”和开头语，是教师发挥主导作用的第一步.通过引入铺垫，给学生概述课程的主要内容，介绍教学知识的来龙去脉，把学生的注意力吸引到即将进行的教学活动中，使学生在学习之初就“胸有成竹”，营造良好的学习氛围.其中，教学内容所包含的数学思想、文化和精神需要重点介绍，这是课程展开的重要依据和线索.

就实变函数课程而言，主要的教学内容包括：集合、点集、测度论、可测函数和积分论等，涉及集合论、拓扑学、分析学等多个专业方向，内容丰富多彩.但第一堂课展现在学生面前的是完全陌生的学术领域，直接讲授知识点本身过于突兀，让学生不易接受.不吝惜一节甚至两节课来解决课程的产生背景、研究内容、研究思路等问题则可以起到事半功倍的效果，为后续的学习开好头.新事物的诞生是旧事物弊端的发展所致，所以黎曼积分的缺陷是重点介绍的内容.为了克服缺陷适应更广泛的应用，年轻数学家勒贝格创立了新的积分——勒贝格积分.和黎曼积分划分定义域相比，勒贝格另辟蹊径划分值域，其主要想法就是为了避免被划分在同一小区间里的变量函数值差别过大，而造成以Dirichlet函数为代表的一些病态函数无法积分.而勒贝格的研究历程也并非一帆风顺，主流数学界的嘲笑讥讽没有阻挡他前进的脚步，他的不懈坚持和刻苦钻研，以及其他数学家、物理学家和工程师的普遍应用，使得越来越多的人接受并认可了这一理论，最终成为近代分析的开端.

又如，在集合论的开篇，介绍康托尔是如何一步一步建立无穷的王国，从一一对应开始定义集合的“个数”，并用来比较无穷集合元素的“多少”，到他发现无理数比有理数“多”，超越数“多”于代数数，用“实无穷”大胆向“潜无穷”挑战.尽管在当时的数学界引起了轩然大波，众多大数学家都不认可，但康托尔最终创立了“集合论”，为近代数学的发展做出了不可估量的贡献.讲清这些数学文化和数学史不仅可以开阔学生的视野，提高学生的数学素养，也可以帮助学生系统理解课程的理论体系，引导学生用正确的观点来看待新生事物，让他们充分体会到实变函数理论发展的必要性，从而有信心、有兴趣学习这门课程.

2.2概念教学性铺垫，注重承上启下

概念教学是数学类课程教学的一个重点和难点，也是基础知识教学的核心内容.正确理解和掌握概念是运用数学解决问题的先决条件，而概念不清则是学生学习的一大障碍.在概念教学时，注重创设情景，提前渗透，通过温故、类比旧知，使新知顺势而发，承上启下自然衔接.

在实变函数课程中，几乎每一章节都有新概念、新定义，对初学者来说是一个难题.例如依测度收敛是实函教学中的一个难点，这种收敛方式与逐点收敛、几乎处处收敛或一致收敛有很大的区别.仅仅从定义本身来介绍概念，符号、术语会让学生难以接受，转而考虑用熟悉的一致收敛的概念来进行铺垫教学.

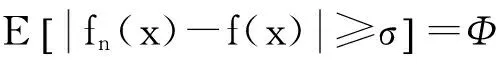
此时

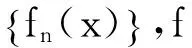
对比两个定义，学生能容易理解依测度收敛的概念，包括定义中很重要的两个量“σ”，“ε”的含义，并且无需证明就清楚一致收敛与依测度收敛之间的关系，为后文要重点讨论的依测度收敛与几乎处处收敛的关系做好铺垫.

在讲解集合列的上下极限时，可以先复习数列的上下极限进行类比学习.对于n维欧式空间中的拓扑概念，如：邻域、开集、闭集、聚点、孤立点等则可借助数学分析中学过的平面有关点集的概念进行推广，让学生感觉到新知识亲切、自然.对于Borel集的概念，定义时若采用从开集出发，取余集，取至多可数交、并后所得到集合的方式，虽然直接但不够深刻.对此先进行有关σ-代数的铺垫，这样学生在学习Borel集的概念时更加容易理解Borel集合和可测集之间的关系.又如在讲解可测函数的定义时要结合已经熟悉的连续函数的概念对比学习，为后续讨论这两类函数之间的关系奠定基础，也使学生更好地理解概念的内涵与外延.

2.3定理结论性铺垫，化解知识难点

建构主义学习理论认为，教学的难点来源于认知的冲突，即正在学习的内容和学生已有的认知水平之间存在较大的落差.特别是定理和结论的证明中包含了较多的知识点，综合性强，技巧性高，因此在教学中需要提前“搭台阶”，在知识的衔接点上加以引导，在证明思路上加以点拨，帮助学生由浅入深、由点到面、由具体到抽象逐步接受新知.将新课内容进行难度分解，提前铺垫相关的知识点和方法技巧，可以降低新课教学的难度，提高课堂教学质量.

实变函数论以集合分析法为主要的研究手段，函数性质的刻画往往通过点集来说明，大量的定理证明，如：可测函数性质，叶果洛夫定理，里斯定理，勒贝格定理等都需要应用集合的关系式.因此及时铺垫利用集合运算来表示函数列极限过程的方法和技巧能有效分解学习难度.又如在探讨有无最大基数集合的问题时，先由有限集合的元素个数小于其幂集所包含的元素个数引导学生发现结论—没有最大基数的集合，再介绍著名的理发师悖论，通过类比使学生能够容易理解证明的思路.

“数的进制”不是实变函数课程专有的教学内容，但在证明集合论中有关集合基数问题时，如康托尔三分集的基数等问题发挥了重要作用.而学生仅仅熟悉整数的二进制转换，对小数的转换涉及等比级数收敛的知识，多数同学不太了解，因此在这部分教学时先补充介绍小数的转换，为后面的证明扫清障碍.此外，还可以延伸介绍和数的进制密切相关的计数方式，告诉学生“半斤八两”的由来，人类喜欢十进制和我们有十个手指有关，如果螃蟹能进化为高级智能动物，那螃蟹的世界多半就是八进制……这些铺垫既拓展学生的视野，也为枯燥的理论教学增加乐趣，融洽了课堂气氛.

此外像勒贝格积分的建立，先从最简单的非负简单函数的勒贝格积分开始，再过渡到非负可测函数的勒贝格积分，最后才是一般可测函数的勒贝格积分，由特殊到一般，循序渐进，逐层铺垫、扩充，易于被学生所接受.鲁津定理的证明推导也采用类似的思路，化繁为简，化难为易.

2.4问题导入性铺垫，启发学生思考

问题导入性铺垫是指提前设置与教学内容密切相关的问题做铺垫，开展启发式教学.设计恰当的问题能调动学生的积极性，激发学生的学习热情，也有利于培养学生发现问题、独立思考、解决问题的能力.

实变函数教学中第一个难点是关于集合“对等和基数”的学习.在研究集合元素的“个数”问题时，先提问学生如何比较有限集合所包含元素的多少？是一个一个的数吗？如果数量过大，如无穷集合数不过来怎么解决？以教室里的同学和课桌为例，启发大家用“一一对等”的方法，简单明了.但对于一般的集合，特别是无穷集合还需要严格定义集合对等的概念，因此“一一对应”的问题值得深入研究.一一对应使得很多看似差别很大的集合却包含相同多的元素，而一一对应的建立又是一件饶有兴趣的工作.在此介绍著名的希尔伯特旅店问题，启发学生对无穷排列问题的思考，为新课的教学埋好伏笔.

2.5延伸拓展性铺垫，扩展学生视野

作为教学的一个重要部分，课堂教学拓展是对已有学习知识的扩充和发展.拓展可以是知识点本身的延续，也可以是知识的应用.在教学中铺垫一些新知和应用，引导学生查阅资料，开展小研讨，撰写科研小论文，培养学生的探究意识和兴趣，开阔学生的视野，激发其学习的兴趣.

在学习了集合论后，学生对集合中元素的“个数”问题有了飞跃性的认识，在完成没有最大基数集合的证明后，提出问题：在连续基数和可数基数之间还有没有其它基数，即希尔伯特23个问题中的第一个——连续统假设.尽管问题的解答已远远超出课本学习的要求，但铺垫此问题的提出背景、研究历史和成果，鼓励学生查找资料，有助于学生了解集合论知识的深化与发展.又如在介绍康托尔三分集后，补充科赫雪花曲线、谢尔宾斯基地毯、英国海岸线等分形几何学的经典例子，让学生了解、欣赏分形几何的美，启发构造类似的例子，感悟数学的魅力，提高学生的现代数学素养.

3结论

在实变函数课程的教学中，铺垫是一种常用的教学方式.铺垫不能代替严格的论述、推导和讲解，但有效的铺垫可以承上启下，降低教学难度，丰富教学内容.铺垫的方式方法并不拘泥于某一种形式，对课程教学有帮助、易于被学生接受的铺垫都有益于教学活动的开展.何时、何地，采用何种方式进行铺垫还值得进一步思考与探讨.

[参考文献]

[1]程其襄，张奠宙，胡善文，等.实变函数与泛函分析基础[M].3版.北京：高等教育出版社，2010.

[2]周民强.实变函数论[M].北京：北京大学出版社，2001.

[3]邓东皋，常心怡.为什么要学习勒贝格积分[J].高等数学研究，2006，19(4)：6-9.

[4]徐西安.改变实变函数教学的一些方法[J].山东教育学院学报，2006，116(4)：103-105.

[5]杨钟玄.浅谈实变函数论教学中应当注意的几个问题[J].天水师范学院学报，2004，24(2)：71-73.

[6]魏勇.浅谈绪论与复习课教学对学生创新思维的培养[J].大学数学，2012，28(10)：154-158.

[7]周性伟.讲授实变函数课的点滴体会[J].高等理科教育，2000，29(1)：42-45.

[8]胡绍宗.实分析教学杂记[J].大学数学，2014，30(3)：107-110.

[9]范洪福.论实变函数解题方法[J].大学数学，2013，29(2)：95-98.

The Method of Foreshadowing in the Teaching of Real Variable Function

FENGYing

(School of Mathematics, Southwest Jiaotong University, Chengdu 611756, China)

Abstract:The method of foreshadowing is an important way in the teaching of real variable function. With the teaching cases, the application of the method of foreshadowing is discussed from the aspects of the teaching introduction, concept, theorem, question and the extension.

Key words:real variable function; teaching method; teaching foreshadowing

[收稿日期]2015-07-30；[修改日期] 2016-03-21

[基金项目]四川省2013-2016年高等教育人才培养质量和教学改革项目：大学数学课程体系与结构优化研究;西安交通大学本科教改项目(1504074)

[作者简介]冯颖(1979-),女，博士，讲师，从事Banach格与正算子理论研究.Email: fengying@home.swjtu.edu.cn

[中图分类号]O174.1

[文献标识码]C

[文章编号]1672-1454(2016)02-0064-04