一类非负矩阵的逆谱问题*
雷英杰,谭迎新
(1. 中北大学 理学院,山西 太原 030051; 2. 中北大学 化工与环境工程学院,山西 太原 030051)
一类非负矩阵的逆谱问题*
雷英杰1,谭迎新2
(1. 中北大学 理学院,山西 太原 030051; 2. 中北大学 化工与环境工程学院,山西 太原 030051)
摘要:给定一个n元复数组σ={λ1;λ2,…,λn},其中L={λ2,…,λn}在复数共轭下保持封闭性质. 非负矩阵的逆谱问题就是确定n阶非负矩阵以σ为谱的充要条件. 如果存在非负矩阵A以σ为谱,就称σ是可以实现的,或A实现σ. 本文意在刻画λ1和L的特征,使得σ={λ1;L}可以被一个n阶非负矩阵实现,其中λ1为可实现矩阵的perron特征值,主要方法是Brauer秩1扰动定理及行和相同的实矩阵的性质,得到具有复数谱集的若干可解条件,同时也结合具体实例证实了所给算法的有效性和实用性.
关键词:非负矩阵; 特征值; 逆谱问题; 构造性算法
非负矩阵的特征值反问题(NIEP)是指非负矩阵的谱的特征刻画问题. 目前,问题的进展是,当给定的谱是一个复数集时,Loewy and London[1]解决了n=3的情形; Reams[2]和Laffey and Meehan[3]仅分别解决了迹为零的n=4,5的情形. 此外,有关复数谱的问题,已经有许多相关的论文[4-11],但该问题仍未得到满意的解决. 在文献[4]中,作者给出了n阶非负矩阵实现n元复数组的若干充分条件和构造性算法,本文试图对该问题进一步探讨.
论文约定σ={λ1;λ2,…,λn}为一个复数集,L={λ2,…,λn}满足复数的共轭封闭性. 若存在一个n阶非负矩阵以σ为谱,则称σ是可以被实现的.
L中的非实复数必须成对出现才可能使得σ被实现. 此外,由perron-Frobenius定理,可令σ中的实数λ1为perron根,即λ1≥|λi|,λi∈L. 方便起见,对L中元素重新排序,使得所有共轭复数对排在一起,且虚部为正的复数靠前. 记
式中: λ2,…,λn已按上述方式作了排序.

1预备知识
引理 1[5]已知(λ1,λ2,…,λn)为n阶矩阵A的特征值,(λk,v)是A的一个特征对,其中v=(v1,v2,…,vn)T,那么,存在n元列向量q,使得λ1,λ2,…,λk+vTq,λk+1,…,λn是矩阵A+vqT的特征值.
该引理称为Brauer秩1扰动定理,在保持其余特征值不变的情形下,通过一个秩1扰动,可改变A的某一特征值,使其成为一个与A相关矩阵的谱集.
引理 2[4]已知σ={λ1;λ2,…,λn}∈ε为一个复数集,假设L中的所有元素为非实数,令
且对所有的i=2,…,n,有
(1)
如果
(2)
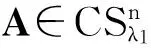
2主要结果


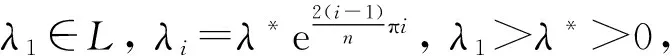





以上定理均限定了给定集σ的维数,强调n为奇数,但当维数不确定或序列L中存在一些不同元的时候,Suleǐmanova可实现判据[6],并给出了其可解条件.

证明由Reλi≤0,Reλi+Imλi≤0,显然有|Reλi|≥|Imλi|,其中λi∈L. 则引理2的证明[4]中所用矩阵B的第一列全为非负元素,且L=0.

Ki,Mi如前所述.

该定理的算法是有效的,例如给定n个有序特征值如下排列
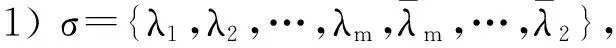

定理 5已知一个复数集σ={λ1;λ2,…,λn}∈ε可以被实现,那么对于任意t∈[0,1),集合{λ1,tL}也可以被实现,尤其被一个正矩阵实现.

显然D>0,且使得{λ1,tL}为其谱集. 证毕.

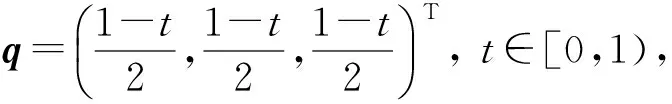
参考文献:
[1]Loewy R, London D. A note on an inverse problem for nonnegative matrices[J]. Linear and Multilinear Algebra, 1978(6): 83-90.
[2]ReamsR.Aninequalityfornonnegativematricesandtheinverseeigenvalueproblem[J].LinearandMultilinearAlgebra, 1996, 41: 367-375.
[3]LaffeyTJ,MeehanE.Acharacterizationoftracezerononnegative5×5matrices,LinearAlgebraAppl., 1999, 302-303: 295-302.
[4]雷英杰, 徐伟孺. 广义行随机矩阵的逆谱问题[J].安徽大学学报(自然科学版),2012, 36(5): 1-5.
LeiYingjie,XuWeiru.Inversespectralproblemforgeneralizedrowstochasticmatrices[J].JournalofAnhuiUniversity(NaturalSciences), 2012, 36(5): 1-5. (inChinese)
[5]BrauerA.Limitsforthecharacteristicrootsofamatrix.IV:Applicationstostochasticmatrices,DukeMath.J., 1952, 19: 75-91.
[6]SulemanovaHR.Stochasticmatriceswithrealcharacteristicvalues[J].Dokl.Akad.Nauk.SSSR, 1949, 66: 343-345.
[7]BorobiaA,MoroJ,SotoR.Negativitycompensationinthenonnegativeinverseeigenvalueproblem[J].LinearAlgebraAppl., 2004, 393: 73-89.
[8]SmigocH.Theinverseeigenvalueproblemfornonnegativematrices[J].LinearAlgebraAppl., 2004, 393: 365-374.
[9]LaffeyTJ,SmigocH.Nonnegativerealizationofspectrahavingnegativerealparts[J].LinearAlgebraAppl., 2006, 416: 148-159.
[10]LaffeyTJ,SmigocH.Spectraofprincipalsubmatricesofnonnegativematrices[J].LinearAlgebraAppl., 2008, 428: 230-238.
[11]MouradB.Onaspectralpropertyofdoublystochasticmatricesanditsapplicationtotheirinverseeigenvalueproblem[J].LinearAlgebraAppl., 2012, 436: 3400-3412.
Inverse Spectral Problem for a Class of Nonnegative Matrix
LEI Ying-jie1, TAN Ying-xin2
(1. School of Science,North University of China,Taiyuan 030051, China;2. School of Chemical and Environmental Engineering, North University of China, Taiyuan 030051, China)
Abstract:Let σ={λ1;λ2,…,λn} be a set of n-tuples with L={λ2,…,λn} being closed under complex conjugation. The nonnegative inverse eigenvalue problem was the problem of determining the necessary and sufficient conditions in order that σ be the spectrum of an entrywise nonnegative n×n matrix. If there is a nonnegative matrix A with σ as its spectrum, we say that σ was realizable and that A realizes σ. In this note, our purpose was to characterize values of some λ1 in terms of L so that σ={λ1;L} is realized by an entrywise nonnegative matrix of order n, where λ1 was the Perron eigenvalue of the realizable matrix. We use Brauer rank one perturbation theorem and the properties of real matrices with same constant row sums to solve this problem. New solvability conditions are derived. Finally,some numerical examples are shown to verify the effectiveness of our corresponding constructive algorithms.
Key words:nonnegative matrices; eigenvalue; inverse spectral problem; construction algorithm
文章编号:1673-3193(2016)02-0109-03
*收稿日期:2015-07-25
作者简介:雷英杰(1970-),男,副教授,博士生,主要从事应用数学、 组合矩阵理论及其在相关学科中的应用研究.
中图分类号:O151
文献标识码:A
doi:10.3969/j.issn.1673-3193.2016.02.003

