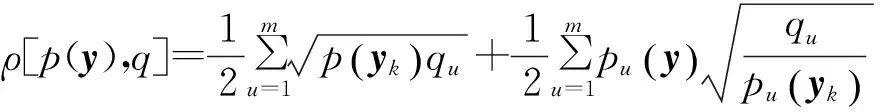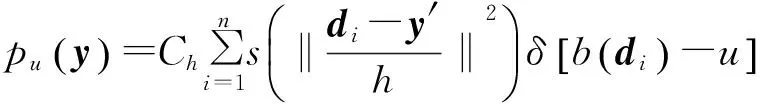基于ELM与Mean Shift的抗遮挡目标跟踪算法

毛晓波,郝向东,梁　静

基于ELM与Mean Shift的抗遮挡目标跟踪算法

毛晓波,郝向东,梁静

(郑州大学 电气工程学院，河南 郑州 450001)

摘要：针对目标跟踪过程中发生遮挡时跟踪出现偏差的情况，在传统Mean Shift跟踪算法的基础上引入极限学习机(extreme learning machine,ELM)，提出了基于ELM与Mean Shift的目标跟踪算法。该算法根据过去3个时刻的目标位置信息，利用ELM预测出目标当前可能位置，代替目标前一时刻位置作为Mean Shift迭代起始点，并在邻域范围内进行迭代，得到目标的真实位置.实验结果表明，与现有的改进算法相比，新算法减少了迭代次数和运算时间，同时在遮挡情况下能够准确定位目标位置并进行跟踪，提高了跟踪系统的实时性和鲁棒性.

关键词：目标跟踪；遮挡；Mean Shift；ELM

0引言

目标跟踪技术是机器视觉的热门课题, 广泛应用于工业生产、国防军事和生活安防等众多领域.遮挡问题是目前目标跟踪的难题之一，遮挡尤其是严重遮挡会直接影响跟踪的准确性和持续性，可能导致目标跟踪发生偏差甚至丢失目标.因此，研究抗遮挡的目标跟踪算法具有重要的理论和实际意义.

Mean Shift算法[1]、光流算法[2]、卡尔曼滤波算法[3]、粒子滤波算法[4]等都能在一定条件下有效地跟踪目标.其中，Mean Shift算法以其无需参数、快速模式匹配的特性被广泛地应用[5].但是,当目标运动速度过快或遮挡较为严重时，传统Mean Shift算法往往会发生目标的定位偏差甚至跟丢.为解决上述问题，研究人员提出了一些有效方法，如在算法中引入模板分块匹配[6]或将Mean Shift算法与滤波算法相结合[7-10]等.这些方法能够提高跟踪算法的抗遮挡能力，但由于需要进行分块跟踪或进行复杂的滤波运算，增加了算法的复杂度，跟踪实时性受到影响.针对以上问题，笔者提出一种基于ELM与Mean Shift的抗遮挡目标跟踪算法，利用ELM的快速学习和预测能力预测目标的运动趋势，以预测出的目标中心作为Mean Shift迭代起始点，通过迭代得到目标当前真实位置.笔者将新算法与基于模板分块匹配的Mean Shift算法和基于卡尔曼滤波的Mean Shift算法作了比较.实验证明，新算法能够在目标高速运动或遮挡情况下快速精确稳定地跟踪目标，具有很好的实时性和鲁棒性.

1Mean Shift算法

Mean Shift算法是一种基于核密度估计的非参数模式匹配算法, 通过建立加权直方图来描述目标的颜色分布[11].该方法利用像素概率密度函数梯度最优化方法,首先选定跟踪目标的区域，计算核函数加权下的目标区域的直方图分布，然后用同样的方法对当前帧的数据密度直方图进行漂移，且通过Mean Shift迭代寻找与目标区域相似性最大的区域，最终实现快速目标定位.

1.1目标模型

Mean Shift跟踪算法利用目标区域的直方图分布来描述目标，根据目标模型和候选模型的相似度进行中心的均值漂移.在第一帧中手动确定包含跟踪目标的区域，设中心坐标为d0;区域中包含n个像素，位置记为{di}i=1,2,…，n；特征值u=1,2,…,m是直方图的颜色索引.则目标模型的特征估计概率密度可表示为

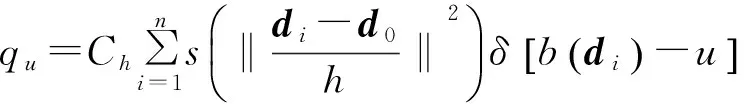
(1)

式中：h为核函数的窗宽，即目标区域的大小；s(·)为核函数的轮廓函数，对靠近中心的区域像素赋予一个大的权值，对远离中心的区域像素赋予越来越小的权值；δ[·]是克罗内科函数，δ[·]用于判断目标区域中像素di的颜色值是否属于第u个单元的颜色索引值，若为1,则是,为0,则不是；Ch为归一化常数，其取值满足

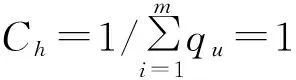
(2)

1.2候选模型

目标运动过程中，每一帧图像中目标可能存在的区域称为候选区域，其核函数窗宽中的特征模型称为目标候选模型.假设第k帧时得到的目标中心为yk，则在第k+1帧中候选模型的特征值为：

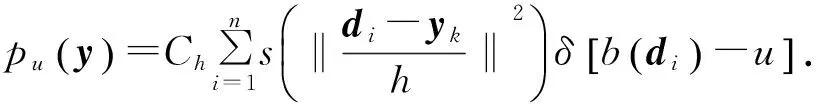
1.3相似度判定函数

在跟踪过程中，Mean Shift算法将候选模型与目标模型进行相似性判别，寻找式(3)中最优的yk，使得pu和qu相似度达到最大.qu和pu的相似度可由如下函数判定：

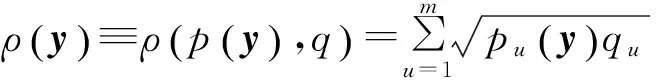
(4)

式中：ρ(y)是Bhattacharyya系数，其值在0～1之间，ρ(y)值越大，表示两个模型相似度越高.目标发生遮挡时，ρ(y)变小，给定遮挡阈值T，当ρ(y)

1.4Mean Shift算法

(5)

(6)

由式(6)可知，相似度函数只随等式右侧第二项中y的变化而变化，与第一项无关.通过Mean Shift算法在邻域内不断迭代，对相似度函数求最大值，即可得到跟踪目标新的位置：

(7)

迭代结束后，得到的yk+1，即为第k+1帧的目标中心.

1.5Mean Shift算法的缺点

在实际应用中，由于Mean Shift算法没有专门有效的抗遮挡机制，当跟踪目标经过遮挡物时，往往会发生目标的跟偏甚至跟丢.另外，当目标高速运动时，Mean Shift算法跟踪效果变差.为此，笔者在Mean Shift算法的基础上引入了ELM算法[12-13]，利用ELM的预测能力较好地解决了上述问题.

2ELM与Mean Shift相结合的算法

2.1ELM的基本原理

若一个标准的单隐层前馈神经网络含有N个训练样本，记为{xi，oi}i=1,2,…,N，其中xi= (xi1,xi2,…,xin)T∈Rn，oi= (oi1,oi2,…,oim)T∈Rm，含有N′个隐层节点，设其激励函数为g(x)，则该神经网络的输出可以表示为

纳税意识是指公民、法人等纳税人对税法确定的纳税义务的认同和看法。纳税意识强，则会积极主动配合税务机关依法纳税；纳税意识弱则会拖延纳税、偷税逃税，对税务机关的征税行为采取隐瞒、欺骗甚至抵抗行为。

式中：wi= (wi1,wi2,…，win)T为输入神经元与第i个隐层节点的输入权值；βi= (βi1,βi2,…，βim)T为第i个隐层节点与输出神经元的输出权值；bi为第i个隐层节点的偏置.

神经网络的理想目标是实际输出与给定样本相等，因此存在βi、wi和bi使得

(9)

式(9)即为ELM的模型，其中,οj为第j个输入样本的对应的输出样本，该模型可用矩阵表示为

Hβ=O.

(10)

H为神经网络的隐层输出矩阵.在ELM中，输入权重wi和隐层偏置bi由系统随机确定，则H被唯一确定.由Moore-Penrose广义逆定理可求出H+，则

β=H+O .

(11)

2.2基于ELM与Mean Shift的抗遮挡目标跟踪算法

在目标运动过程中，第t时刻目标的位置与其上一时刻的位置、速度和加速度有关，即可以通过这3个参数确定目标当前时刻的位置.而这3个参数包含在第t-1、t-2、t-3时刻的目标位置信息中，因此，由前3时刻目标的位置可以预测出第4时刻目标的位置.

首先,通过对无遮挡目标的精确跟踪得到一组目标运动轨迹，为了提高样本精确度，采用手工逐帧确定.取连续200组中的前160组位置坐标作为ELM的训练样本，将连续3组坐标作为输入，第4组作为输出来训练ELM神经网络.利用后40组作为测试样本，通过不断调节隐层节点数使预测达到最优.同理，对遮挡目标进行训练，训练样本和测试样本依然分别取160组和40组.调节隐层节点数，使两个训练集合的预测结果最佳.通过试验，当隐层节点设为30时,预测值达到最优.

(12)

于是，式(7)变为

(13)

同时计算ρ(y)并与遮挡阈值T进行比较，若ρ(y)≥T，则继续执行；若ρ(y)

3仿真结果分析

在2.10 GHz主频4 GB内存的Windows8操作系统电脑上使用Matlab2010，对笔者提出的算法进行了测试实验，并在相同条件下与基于模板分块匹配的Mean Shift算法和基于卡尔曼滤波的Mean Shift算法跟踪效果进行了对比.

为验证跟踪结果的实时性，我们对公路上高速行驶的汽车进行了20次跟踪，统计3种算法对第11帧到110帧共计100帧目标进行20次跟踪的平均迭代次数，并对跟踪效果进行了对比.表1显示了3种不同算法的平均迭代次数对比结果.通过对比可以发现，由于新算法采用了位置预测，迭代起始位置与目标实际位置的距离大大减少，因此比基于模板分块匹配的Mean Shift算法迭代次数平均减少1.20次；同时,新算法的位置预测方法较卡尔曼滤波更为简便，一定程度上简化了融合算法且计算效率有所提高， 比基于卡尔曼滤波的Mean Shift算法平均减少0.76次.

表1　3种算法迭代次数

表2为3种算法分别对100帧视频进行20次跟踪的平均时间.由表2可知，新算法平均跟踪时间是4 918 ms，比两种已有改进算法分别减少17.9%和7.2%.

表2　3种算法跟踪时间

图1为3种算法跟踪效果，分别取第20、40、60、80帧图片.表3为3种算法的跟踪误差，表示跟踪位置和实际位置中心的距离，实际位置采用手工逐帧确定.由表3可知，新算法与基于模板分块匹配的 Mean Shift算法跟踪误差近似，明显小于基于卡尔曼滤波的Mean Shift算法.

图1　高速运动车辆跟踪结果对比

算法Frame20Frame40Frame60Frame80分块算法5.38518.60140.79252.631滤波算法6.70824.83961.221107.415 新算法6.00017.80444.68954.918

图2为3种算法对公路上被遮挡车辆进行跟踪的结果，分别取第5、17、29、43帧图片.表4为3种算法的跟踪误差.由表4可以看出，当目标发生遮挡时，3种算法跟踪误差变化较为剧烈，此时新算法的跟踪误差为66.129，明显小于另外两种改进算法.遮挡结束后恢复到正常跟踪，3种算法跟踪误差均变小.

图2　遮挡车辆跟踪结果对比

算法Frame5Frame17Frame29Frame43分块算法3.00031.32181.02549.980滤波算法4.12337.121110.02377.621新算法2.82832.24966.12941.976

表5为3种算法跟踪60帧车辆遮挡视频所用时间，新算法跟踪时间比另外两种改进算法分别减少18.5%和7.5%.

表5　3种算法跟踪时间

图3为3种算法对被遮挡的行人进行跟踪的结果，取第20、40、50、70帧进行比较.由图3可以看出，由于跟踪过程中行人被完全遮挡，基于模板分块匹配的Mean Shift算法无法进行子块匹配，造成了错误的跟踪，丢失了目标；而基于卡尔曼滤波的Mean Shift算法和新算法在目标被遮挡时自动以预测的目标位置为起点继续跟踪，遮挡结束后恢复正常跟踪，因此能够较好地跟踪目标.

图3　行人遮挡跟踪结果对比

以上实验表明，当目标高速运动或发生遮挡时，新算法具有更好的实时性和鲁棒性.

4结论

笔者提出一种基于ELM与Mean Shift的抗遮挡目标跟踪算法，解决了Mean Shift算法在目标发生遮挡时跟踪性能变差的问题.该算法利用目标的历史位置信息，通过神经网络预测出当前位置信息，所需信息少，计算量小，有效地减少了迭代次数，在目标发生遮挡时以预测位置信息继续跟踪，能够准确跟踪目标.实验证明，新算法能够在目标发生严重遮挡时准确跟踪目标，具有很好的实时性和鲁棒性，并且与现有的改进算法相比，具有一定的优势.

神经网络具有强大的自学能力、联想能力和计算能力，将神经网络应用到目标跟踪技术中，突破传统算法的限制，使跟踪系统更加智能化，为解决目标跟踪问题提供了新方法，对于处理目标跟踪过程中的遮挡问题，提高复杂场景下目标跟踪的稳定性具有重要意义.笔者并没有考虑多目标跟踪的问题，因此下一步将考虑对多个目标进行跟踪时如何利用神经网络实现有效跟踪.

参考文献：

[1]何志勇，蔡乐才，许继家．基于Mean Shift算法跟踪视频中运动目标[J]．郑州大学学报(理学版)，2010，42(1)：38-40，48．

[2]李剑峰，黄增喜，刘怡光．基于光流场估计的自适应Mean-Shift目标跟踪算法[J]．光电子·激光，2012，23(10)：1996-2002．

[3]WENG S K，KUO C M，TU S K．Video object tracking using adaptive Kalman filter[J]． Journal of visual communication and image representation，2006，17(6)：1190-1208．

[4]屈鉴铭，刘志镜，贺文骅．结合有向场景运动模式的粒子滤波行人跟踪方法[J]．西安交通大学学报，2014，48(12)：74-79．

[5]袁霄，王丽萍．基于MeanShift算法的运动人体跟踪[J]．计算机工程与科学，2008，30(4)：46-49．

[6]颜佳，吴敏渊，陈淑珍，等．应用Mean Shift和分块的抗遮挡跟踪[J]．光学 精密工程，2010，18(6)：1413-1418．

[7]章学静，陈禾，杨静．结合卡尔曼滤波和Mean Shift的抗遮挡跟踪算法[J]．北京理工大学学报，2013，33(10)：1056-1061．

[8]张伟丽，江春华，郝宗波．基于改进的均值漂移和卡尔曼滤波的目标跟踪算法[J]．计算机应用与软件，2014，31(5)：240-243．

[9]HE J W,YANG Y Y．Signal Processing, communications and computing: ICSPCC2014[C] ∥Multi-interative tracking mathod using meanshift based on kalman filter.Guilin，2014：22-27．

[10]权义萍，金鑫，张蕾，等．基于Mean-Shift的卡尔曼粒子滤波车辆跟踪算法研究[J]．计算机应用与软件，2014，31(9)：236-252．

[11]杨杰，张翔．视频目标检测和跟踪及其应用[M]．上海：上海交通大学出版社，2012．

[12]王杰，毕浩洋．一种基于粒子群优化的极限学习机[J]．郑州大学学报(理学版)，2013，45(1) ：100-104．

[13]胡义涵，张小刚，陈华，等．一种基于鲁棒估计的极限学习机方法[J]．计算机应用研究，2012，29(8)：2926-2930．

Target Tracking Algorithm Based on Mean Shift with ELM

MAO Xiaobo, HAO Xiangdong, LIANG Jing

(School of Electrical Engineering,Zhengzhou University，Zhengzhou 450001,China)

Abstract:In view of the problem of object deviation when occlusions occur during the target tracking, a new algorithm using Mean Shift with ELM is proposed. According to the formal information of the object’s location, current possible location was predicted by ELM, the iteration was started from the possible location instead of formal location, and the object’s real center is calculated by mean shift algorithm. The simulation results show that proposed algorithm can track precisely target occluded, operation time and number of iteration are reduced so that efficiency and robustness are improved.

Key words:target tracking; occlusion; Mean Shift; ELM

收稿日期:2015-03-10；

修订日期：2015-05-20

基金项目：国家自然科学基金资助项目(61473266); 河南省教育厅科学技术研究重点项目资助计划(14A410001)

作者简介:毛晓波(1965—)，男，河南开封人，郑州大学教授，博士，主要从事仿生机器视觉研究，E-mail: mail-mxb@zzu.edu.cn.

文章编号:1671-6833(2016)01-0001-05

中图分类号：U461.6

文献标志码：A

doi:10.3969/j.issn.1671-6833.201503043

引用本文:毛晓波,郝向东,梁静.基于ELM与Mean Shift的抗遮挡目标跟踪算法[J].郑州大学学报(工学版)，2016,37(1):1-5.