微粗糙基底上多层涂层光散射偏振建模与特性研究

曹 慧， 高 隽， 王玲妹， 王 驰

合肥工业大学图像信息处理研究室， 安徽 合肥 230009

微粗糙基底上多层涂层光散射偏振建模与特性研究

曹 慧， 高 隽， 王玲妹*， 王 驰

合肥工业大学图像信息处理研究室， 安徽 合肥 230009

为满足多层涂层目标的偏振探测需求， 基于一阶矢量扰动理论， 结合偏振传输矩阵， 建立微粗糙基底上多层涂层的光散射偏振双向反射分布函数模型， 研究多因素影响下两种典型涂层目标， 单层减反射涂层和多层高反射涂层的光散射偏振特性， 结果表明单层减反射涂层目标的偏振度受观测位置影响， 峰值左侧的偏振度较之裸基底增大， 右侧反之， 探测不同观测角下的偏振度可区分无涂层和涂层目标。 不同观测角和入射波长下， 多层高反射涂层目标的偏振度与涂层层数和涂层光学厚度显著相关， 层数增加， 多层涂层在镜反射附近具有去偏作用。 仿真结果符合测量数据， 验证了多涂层目标散射偏振模型的正确性与合理性， 为实现多涂层目标偏振探测和反射隐身技术提供理论依据。

散射； 多层涂层目标； 偏振双向反射分布函数； 偏振度； 穆勒矩阵

引 言

随着高科技隐身技术和军事伪装材料[1]的发展， 多层涂层目标越来越受到广泛的关注， 探测多层涂层目标的偏振特性， 可以获取传统光强探测方法无法提供的新信息， 提高目标探测精度。 因此， 对多层涂层目标光散射进行偏振双向反射分布函数(polarized bidirectional reflectance distribution function， PBRDF)建模和分析， 获取目标的偏振特性， 在目标探测、 军事目标隐身、 计算机视觉[2]等领域都具有重要意义。

双向反射分布函数(bidirectional reflectance distribution function， BRDF)是反射介质本质属性的表达， 描述表面的反射能量分布情况。 PBRDF在BRDF基础上发展起来， 描述散射的偏振特性[3]， 是获取目标偏振探测信息的有力手段。 关于目标表面光散射PBRDF的建模与分析， 国内外学者都展开了大量的研究。 Priest和Germer[4]从微面元模型和菲涅尔反射出发， 通过坐标变换和琼斯矩阵将标量Torrance-Sparrow模型[5]拓展为基于微面元的PBRDF模型， Hyde等[6]进一步增加了遮蔽和掩饰因子以及漫反射分量。 Prokopenko[7]等基于微面元PBRDF模型， 研究了粗糙表面的反射穆勒矩阵、 Stokes矢量以及偏振度的变化。 Germer[8]在Elson提出的针对微粗糙表面的一阶矢量扰动理论的基础上建立了微粗糙表面和表面含有缺陷粒子的PBRDF模型， 提出了用PBRDF矩阵分量进行次表面缺陷、 微粒污染或粗糙表面诱导下等不同散射机理的区分。

实际中， 目标表面一般都涂有不同作用的涂层。 在目标隐身和伪装以及材料制备中， 涂层起到改变表面反射特性或防止材料腐蚀等作用。 Ellis[9]针对油漆涂层的反射模型， 建立了一种由镜面介电层覆盖的朗伯反射体组成的光滑涂层PBRDF模型， 考虑表面散射和体散射。 Germer等[10]研究了具有一层涂层的表面偏振散射特性， 分别计算了涂层与基底的散射琼斯矩阵。 巩蕾等[11]提出一种粗糙基底上不同涂层的PBRDF模型， 对不同涂层的光学特性进行研究， 反演基底的光学信息。 陈超等在微面元模型的基础上， 通过实验研究， 结合遗传LM算法， 建立了涂层目标光谱PBRDF模型， 可以预测任意探测几何条件下的光谱PBRDF值。 这些针对涂层目标表面的PBRDF研究多集中在粗糙基底上涂有单层涂层的目标上， 建模方法主要有微面元法， 多参量模型法以及基于矢量扰动理论的电磁解法， 但未考虑多层涂层目标表面的偏振散射情况。 针对实际应用中涂有多层复杂涂层的目标表面偏振探测的需要， 建立多层涂层目标的偏振散射模型以及三维空间散射偏振特性分析是涂层目标偏振研究中的关键。

基于多层涂层目标光散射的矢量扰动理论， 结合琼斯矩阵和穆勒矩阵， 建立微粗糙基底上多层涂层的光散射PBRDF理论模型， 着重从偏振探测角度分析不同观测几何和入射波长下涂层目标的变化规律， 研究多因素影响下典型单反射涂层和多层高反射涂层的光散射偏振特性， 对研究多层涂层目标的偏振探测和反射隐身技术有重要意义。

1 多层涂层目标PBRDF模型

1.1 PBRDF

BRDF描述了从某一方向入射的光波， 经目标表面反射后， 反射能量在上半球空间的分布情况。 图1为BRDF的几何关系示意图。 由图可知波长为λ的入射光， 以入射角θi照射到目标表面， 散射角和方位角分别为θr和φr。

Fig.1 Geometrical schematic of BRDF

PBRDF在BRDF的基础上， 描述了散射的偏振特性， 是获取目标偏振探测信息的有力手段。 可以用偏振散射琼斯矩阵S建立光波入射场和散射场之间的联系[12]

(1)

其中下标s表示电场分量垂直于入射面， p表示电场分量平行于入射面， 上标inc表示入射分量， scat表示散射分量，R表示散射体到探测者的距离，k=2π/λ。 当入射光和反射光用Stokes矢量描述时， PBRDF可以用Mueller矩阵进行表示[3]， 建立光波入射场和散射场之间的联系

(2)

其中Φi为入射Stokes矢量， dΦr为微分散射Stokes矢量， dΩ为微分立体角， cosθr为习惯性因子，Fr为穆勒矩阵形式PBRDF， 具体表示为

(3)

其中S代表琼斯矩阵，M(S)为琼斯矩阵经公示转化所得的穆勒矩阵[12]，A为光线散射区域的面积。

不同散射方向的偏振度是描述目标偏振探测信息的重要表征方式， 偏振度[12]定义如下： 若散射光线的Stokes矢量的四个分量分别为Φ0，Φ1，Φ2，Φ3， 则用Stokes矢量形式表示的偏振度为

(4)

1.2 多层涂层目标PBRDF建模

一阶矢量扰动理论[13]可以用来描述粗糙界面起伏很小的情况下的光散射强度变化。 本工作基于多层介电薄膜散射的一阶矢量扰动理论， 结合偏振传输矩阵， 建立了微粗糙基底上多层涂层的表面光散射PBRDF模型。 粗糙基底上多层涂层目标几何模型如图2(a)所示， 基于矢量扰动理论的光散射示意图如图2(b)所示。

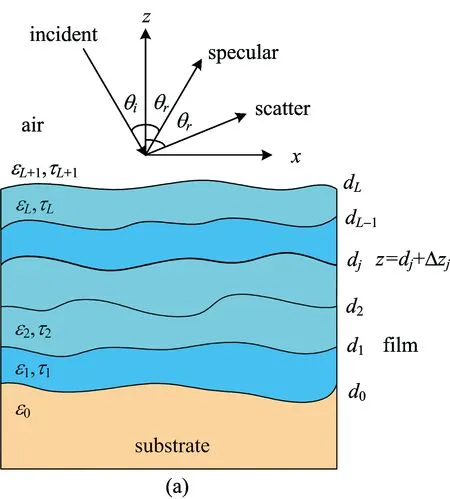
Fig.2 (a) Geometrical schematic of multilayer films on rough substrate; (b) Schematic of light scattering through multilayer films

图2可知， 波长为λ的光波以角θi入射， 散射角为θr， 方位角为φr， 该多层涂层目标共有L+2层， 每层界面j(j=0, 1, 2, …,L+1)的介电常数为εj。j=0表示基底；j=1→L分别表示1→L层涂层， 每层涂层的厚度用平均物理厚度τj表示；j=L+1表示入射介质层， 一般为空气。 由于基底是微粗糙的， 一个微粗糙界面可以用z=dj+Δzj来表示， Δzj是描述界面粗糙度的随机变量。

采用一阶矢量扰动理论计算多层涂层的光散射过程时， 需要同时考虑零阶电场和一阶电磁场的共同作用， 逐层求解基底和每层涂层的特征矩阵， 进而计算可得最终散射矩阵。 微粗糙界面多层薄膜的光散射BRDF[14]定义为

(5)

基于上述微粗糙界面多层介电薄膜的光散射BRDF求解方法， 构建多层涂层目标表面光散射PBRDF模型。 结合一阶矢量扰动理论中p-偏振，s-偏振分量的推导过程及式(5)， 引入散射琼斯矩阵

(6)

式中的suv(u, v=s, p)为散射矩阵元素

(7)

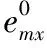
(8)

其中r为二维表面波矢量，a和b为与表面相关长度和均方根粗糙度有关的量。 计算裸基底和1～L层涂层的散射琼斯矩阵时， 分别取m=0和m=1→L代入式(6)—式(8)可得。

1.3 多层涂层目标的界面相关模型

通过上述模型计算可以获得基底和每层涂层的散射琼斯矩阵， 就目标探测而言研究一个基底上方涂有多层涂层的目标光散射情况， 需要考虑界面间的粗糙度函数， 对整体涂层目标进行界面相关性建模。 对于n个不同的局部散射场， 运用不同散射源间的相位关联度将散射场叠加， 得到的散射穆勒矩阵描述为[10]

(9)

其中Sm代表第m个局部场(m=1, …,n)的散射琼斯矩阵；M(Sm)为该琼斯矩阵转化所得的穆勒矩阵；Cmm′代表两个局部场之间的相位关联度。 根据式(9)， 讨论多层涂层界面的两种极限情况， 建立两种界面相关模型。

(1)完全相关模型

该模型假设每层涂层界面完全复现基底表面形状， 即式(9)各局部场之间的相位关联度Cmm′=1， 并结合琼斯穆勒转换公式[12]， 推导得完全相关模型的PBRDF穆勒矩阵为

(10)

其中Ssub，Sfilm分别为基底层和各个覆盖涂层的散射琼斯矩阵。

(2)完全不相关模型

该模型假设各涂层界面不规则缺陷的随意起伏是完全独立不相关的， 但各界面的功率谱密度相同， 即式(9)中各局部场之间的相位关联度Cmm′=0， 得到完全不相关模型的PBRDF穆勒矩阵为

(11)

2 结果与讨论

采用模型仿真研究其模型的正确性， 同时分析多因素影响下两种典型反射涂层目标， 单层减反射涂层和多层高反射涂层的反射强度和偏振度变化， 为涂层目标偏振探测提供理论依据。

2.1 多层涂层目标PBRDF模型正确性验证

为验证上述理论模型的正确性, 采用计算机仿真的方法对模型的光学因子和偏振度进行仿真计算， 并分别与文献[15]中的矢量散射理论方法和文献[16]中实测数据进行对比。

图3(a)为玻璃基底上涂有MgF2和ZnS交替涂层的高反射涂层G(HL)5HA的光学因子比较结果， 入射光为s偏振光(斯托克斯矢量(1, -1, 0, 0))， 波长λ=0.632 8 μm， 玻璃的折射率n=1.52， MgF2涂层折射率n=1.38， ZnS涂层折射率n=2.35， 光学厚度λ/4， 从比较结果来看， 数值模拟结果与对比结果有较好的吻合。

Fig.3 (a) Optical factor of multilayer high-reflection films at different scattering angles;(b) Degree of polarization of green paints at different incident angles

图3(b)为绿漆涂层的偏振度随入射角变化的仿真结果和实际测量曲线。 实线表示涂层层数为10的绿漆涂层的仿真结果， 仿真实验中每层涂层光学特性相同， 总厚度设置与文献[16]中绿漆涂层的厚度相同； 点线为来源于新墨西哥州立大学光电研究实验室研发的成像偏振仪[17]的实测数据。 其中绿漆表面的复折射率为n=1.39-0.34i， 入射光波长为0.65 μm。 从比较结果来看， 数值模拟结果在小角度入射时比实验结果略高， 这是由于实际测量中绿漆涂层的表面漫反射作用使得在小角度处有一定程度的去偏效果， 且实际测量表面也不是一个理想高斯面， 但总体看来仿真结果与实测结果有较好的吻合。

2.2 单层减反射涂层目标PBRDF仿真分析

上述多层涂层目标的偏振模型同样适用于涂有单层涂层的目标表面， 图4所示为K9玻璃上涂有一层MgF2涂层的单层减反射涂层结构， 分别表示不同入射角下涂层目标的完全相关模型， 完全不相关模型以及裸基底中穆勒矩阵的反射强度分量m00和偏振度随观测角的变化曲线。 其中入射光为波长λ=0.633 μm的自然光， K9玻璃的折射率n=1.52， MgF2折射率n=1.38， 涂层厚度d=0.114 7 μm。

图4可以看出反射强度分量m00在镜反射处出现峰值，完全不相关模型下的m00分量随着入射角的增大先减小后增大， 反射强度始终大于完全相关模型的反射强度。 由于涂层厚度较薄， 且只有一层， 完全相关模型的特性与真实涂层目标特性吻合， 其反射强度始终小于裸基底的反射强度， 即减反射特性， 但反射强度随着入射角的增大逐渐逼近裸基底的强度值。

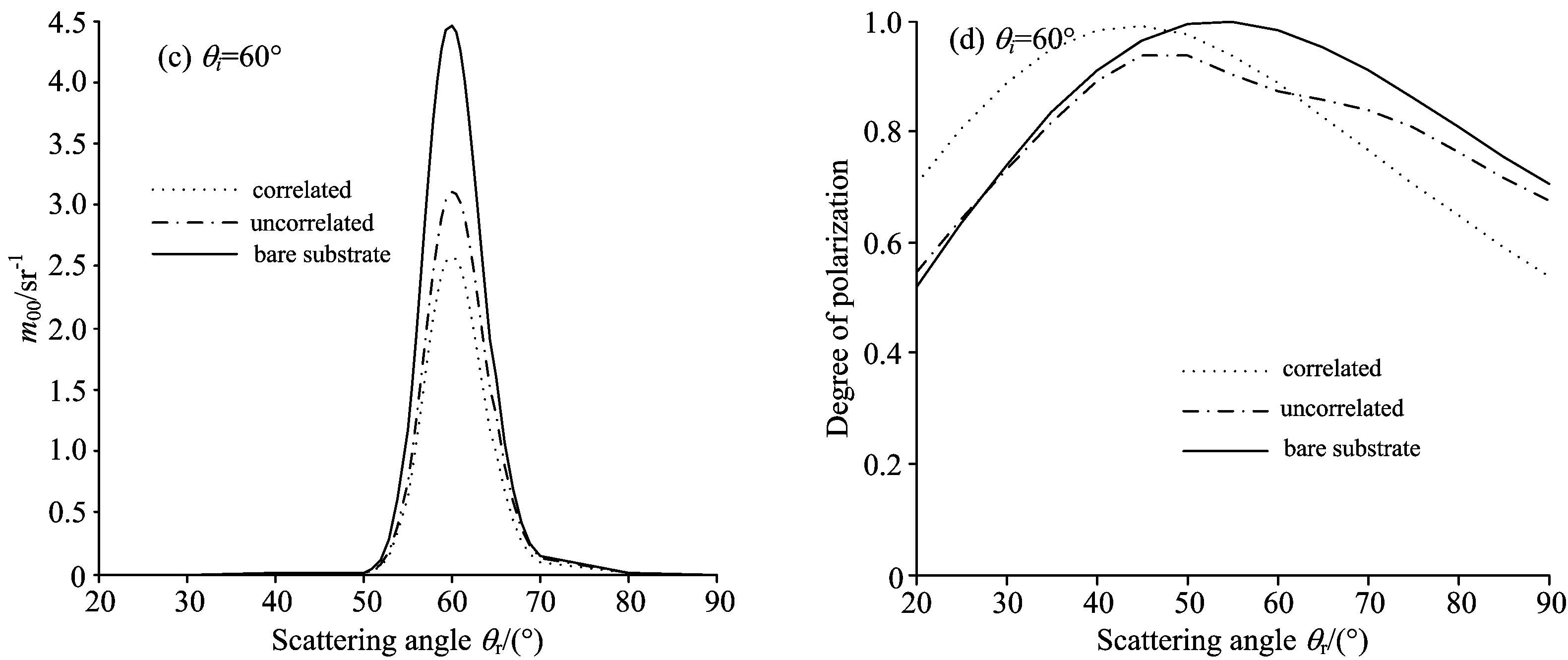
Fig.4 Reflection intensity component m00 and degree of polarization of MgF2 film on K9 glass at different scattering angles

该涂层目标的偏振度随观测角的增大先增大后减小， 最大值接近于1。 偏振度峰值出现的位置随着入射角的增大逐渐向观测角较小的位置移动。 涂层目标的完全相关模型和裸基底模型的偏振度变化趋势大体相同， 但目标的偏振度值随着入射角的增大， 在观测角较小的区域较裸基底增大， 在观测角较大的区域反之。 通过探测不同观测角处的偏振度有助于区分涂层目标和无涂层目标。

2.3 多层高反射涂层目标PBRDF仿真分析

(1)涂层层数对反射强度和偏振度影响

图5—图7为铝基底上涂有高低折射率交替的ndcosθ=λ/4光学厚度的高反射涂层目标G(LH)sA。 其中G代表微粗糙基底， 实验中选取复折射率n=1.27-7.28i的铝基底，s代表高低折射率交替的介质涂层数， 高折射率涂层为ZnS， 低折射率涂层为MgF2， 入射介质为空气， 入射光为波长λ=0.633 μm的自然光， 入射角为60°。

图5为不同涂层层数的目标反射强度和偏振度随观测天顶角变化曲线图， 此时观测方位角设置为0°。 图中可以看出涂层层数增加， 目标反射强度分量m00逐渐增大， 符合高反射涂层的特性， 且反射强度在镜反射位置存在峰值。 随着层数的增加镜反射附近的偏振度逐渐减小， 偏离该位置的偏振度逐渐增大， 且偏振度以镜反射位置为中心存在一定的对称性分布。 因此， 多层涂层目标的偏振特性与无涂层目标的偏振特性存在差异， 且目标的偏振特性与涂层数目密切相关。

图6为不同观测几何下， 两层MgF2和ZnS涂层目标的反射强度和偏振度随观测天顶角和方位角变化的三维示意图。 从图中可以看出， 观测方位角和天顶角同时对观测的多层涂层目标的反射强度和偏振度产生影响。 反射强度在镜反射的天顶角位置出现峰值， 当观测方位角小于10°时， 随着方位角的增大峰值急剧下降， 其后反射强度近似为0。 偏振度总体随着观测天顶角先迅速增加再逐渐降低， 在镜反射附近出现两个对称的波谷后， 数值逐渐增大； 而观测方位角在0°～60°时对偏振度影响较大， 0°～50°范围内， 偏振度随着方位角的增大递增， 镜反射附近的峰值增大尤为明显， 50°～60°范围内偏振度迅速降低至近似为0， 在60°～90°时对偏振

Fig.5 (a) Reflection intensity component m00; (b) Degree of polarization of MgF2 and ZnS multilayer films on aluminum substrate at different scattering angles

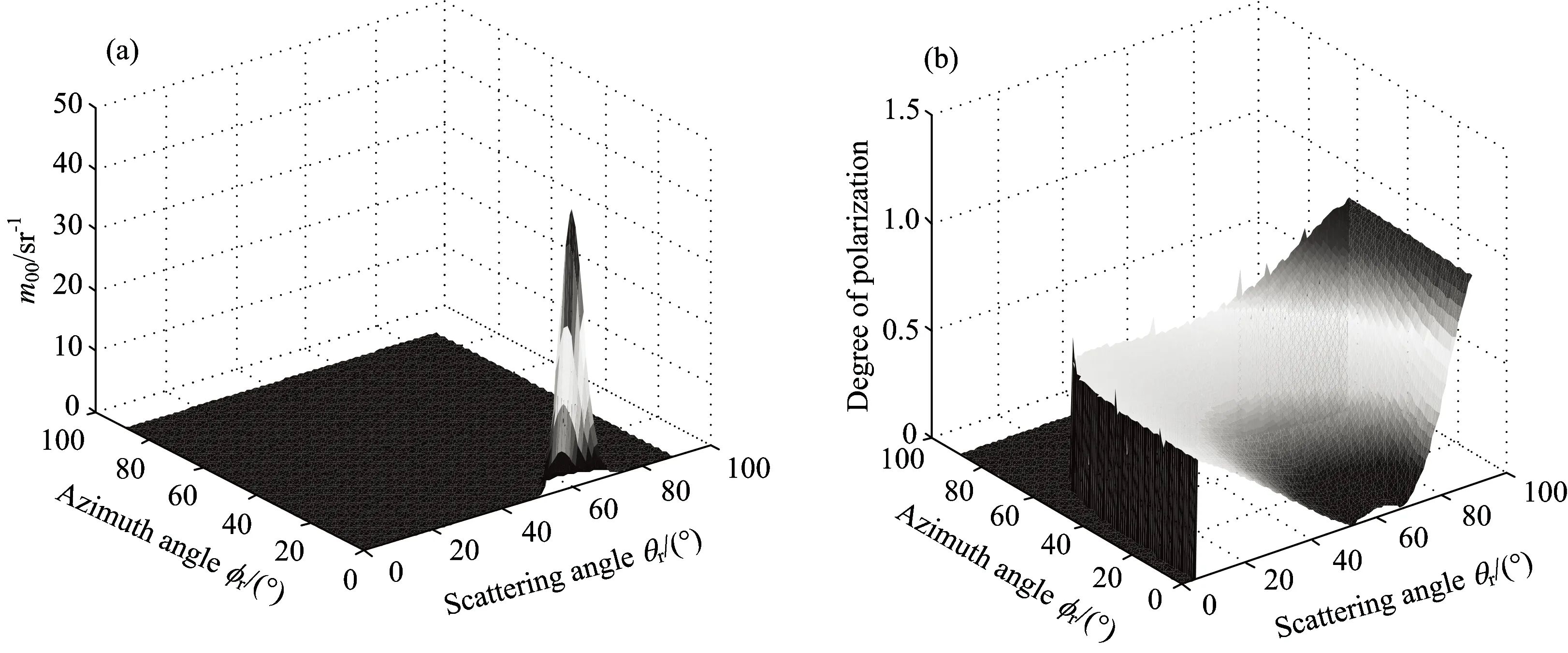
Fig.6 (a) Reflection intensity component m00; (b) Degree of polarization of MgF2 and ZnS two-layer films on aluminum substrate at different observation geometries

度无明显影响， 这为不同观测几何下的偏振探测提供了详细的理论依据。

图7为不同涂层层数的目标反射强度和偏振度随入射光波长变化的曲线图， 设定观测角为60°， 方位角为0°。 图7可以看出随着波长的增加， 反射强度逐渐降低， 而偏振度随波长的变化趋势与之相反。 涂层层数增加， 反射强度逐渐增大， 但偏振度逐渐减小， 当涂层层数达到5对时， 整个入射波段内偏振度近似为0， 说明镜反射位置多层涂层具有消偏作用， 此时入射波长对偏振度变化几乎无影响。

(2)涂层光学厚度对反射强度和偏振度影响

图8为不同涂层光学厚度下， 铝基底上涂有两层MgF2和ZnS涂层的反射强度和偏振度随观测角变化曲线图， 其中入射光为波长λ=0.633 μm的自然光， 入射角60°， 观测方位角0°。 图中可知， 光学厚度为λ/4的涂层反射强度最高，λ/8和λ/2光学厚度的涂层目标反射强度变化曲线几乎重合， 光学厚度为λ/16时反射强度最低， 故大多数高反射涂层目标选取λ/4光学厚度的涂层提高目标反射率， 光学厚度偏离λ/4越远， 反射强度越低。 涂层目标偏振度在光学厚度为λ/4和λ/2时变化趋势近似相同， 较其余光学厚度的涂层在同一观测角下偏振度最大， 且镜反射附近存在两个对称的偏振度波谷。 光学厚度为λ/8的涂层目标偏振度最低， 并伴随着波谷向观测角较小的位置移动。

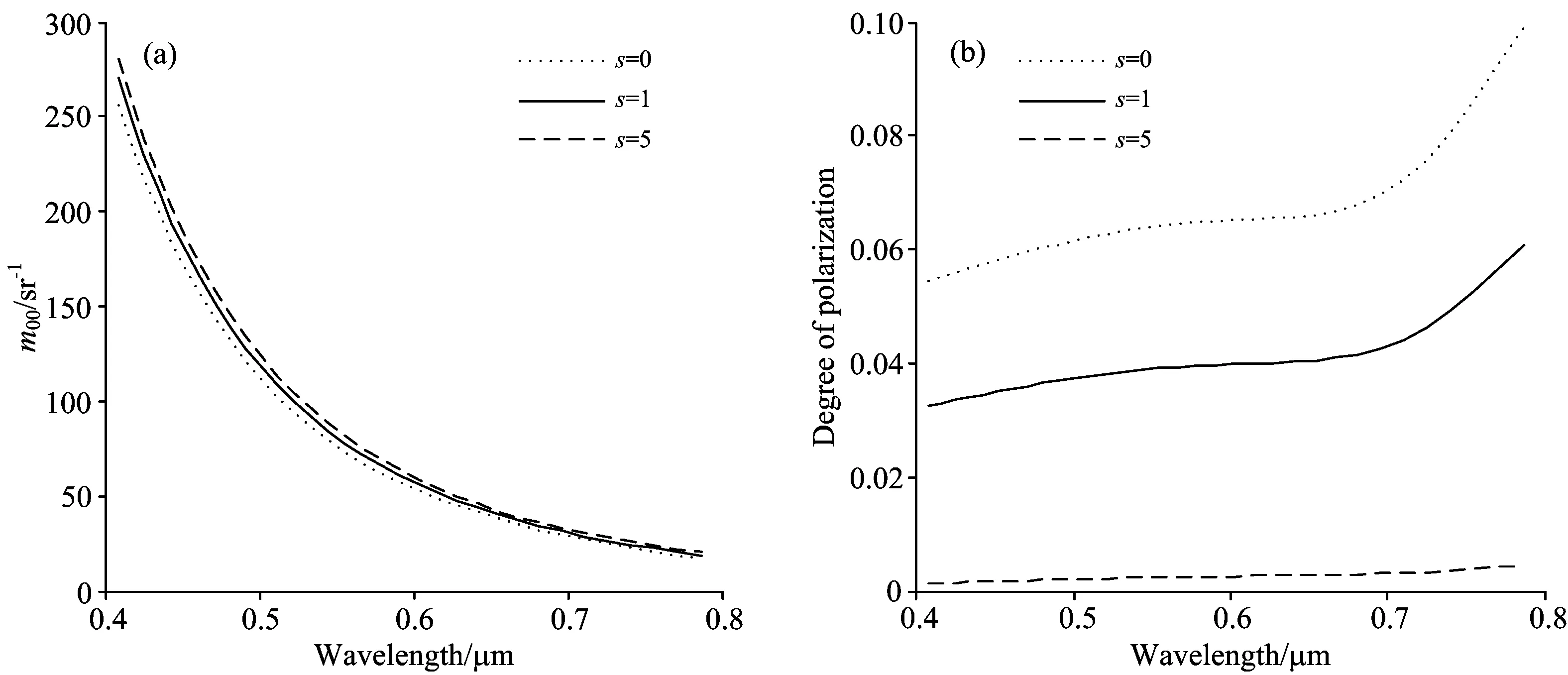
Fig.7 (a) Reflection intensity component m00; (b) Degree of polarization of MgF2 and ZnS multilayer films on aluminum substrate at different wavelengths

Fig.8 (a) Reflection intensity component m00; (b) Degree of polarization of multilayer reflection films verses scattering angles with different optical thicknesses

3 结 论

基于一阶矢量扰动理论， 针对多层涂层目标偏振探测的需要， 采用偏振传输矩阵， 建立了微粗糙基底上多层涂层的偏振双向反射分布函数的理论模型， 并通过实验对比验证了模型的正确性。 运用上述多层涂层目标的偏振建模方法， 讨论了两种界面相关模型的计算， 针对两种典型的反射涂层目标， 单层减反射涂层和多层高反射涂层， 仿真分析了多因素影响下反射强度与偏振度的变化规律， 实验结果表明：

(1)单层减反射涂层目标， 完全相关模型的反射强度随着入射角的增大逐渐逼近裸基底的反射强度， 而偏振度受观测位置影响， 在观测角较大和较小位置呈现相反的变化， 且峰值左侧的偏振度较之裸基底增大， 右侧反之， 不同观测角下目标偏振度的探测有助于区分无涂层和涂层目标。

(2)多层高反射涂层目标， 涂层层数和涂层本身的光学特性显著影响探测目标的反射强度和偏振度。 不同观测角下， 涂层目标层数增加， 反射强度增大， 而偏振度以镜反射位置为中心呈现一定对称性分布， 靠近镜反射位置层数越多， 偏振度越低， 偏离镜反射位置偏振度变化规律相反。 不同入射波长下， 目标偏振度总体随波长的增大逐渐增大， 但层数越多， 镜反射附近多层涂层的散射作用使得目标退偏， 此时波长对其几乎无影响。 光学厚度为λ/4的涂层目标， 较之其余光学厚度涂层， 反射强度和偏振度同时达到最大。 以上结论为多层涂层目标的偏振探测提供了理论依据， 弥补了光强探测获取信息的单一性， 为反射隐身技术和伪装目标三维空间探测提供参考。

[1] YAN Yun-hui, WANG Zhan, DONG De-wei(颜云辉, 王 展, 董德威). China Mechanical Engineering(中国机械工程), 2012, 23(17): 2136.

[2] Collin C, Pattanaik S, LiKamWa P， et al. Proceedings of the 2014 Graphics Interface Conference， Canadian Information Processing Society, 2014. 201.

[3] ZHAO Yong-qiang, PAN Quan, CHENG Yong-mei(赵永强, 潘 泉, 程永梅). Imaging Spectropolarimentric Remote Sensing and Application(成像偏振光谱遥感及应用). Beijing: National Defense Industry Press(北京： 国防工业出版社), 2011. 107.

[4] Priest R G, Germer T A. Proceedings of the 2000 Meeting of the Military Sensing Symposia Specialty Group on Passive Sensors, 2000, 1: 169.

[5] Torrance K E, Sparrow E M. J. Opt. Soc. Am., 1967, 57(9): 1105.

[6] Hyde M W, Schmidt J D, Havrilla M J. Optics Express, 2009, 17(24): 22138.

[7] Prokopenko V T, Alekseev S A, Matveev N V， et al. Optics and Spectroscopy, 2013, 114(6): 961.

[8] Germer T A. Applied Optics, 1997, 36(33): 8798.

[9] Ellis K K. JOSA A, 1996, 13(8): 1758.

[10] Germer T A. JOSAA, 2001, 18(6): 1279.

[11] GONG Lei, WU Zhen-sen(巩 蕾, 吴振森). Acta Optica Sinica(光学学报), 2011, 31(10): 251.

[12] CHEN Chao, ZHAO Yong-qiang， LUO Li， et al(陈 超, 赵永强, 罗 丽, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2010, 30(3): 729.

[13] LIAO Yan-biao(廖延彪). Polarized Light(偏振光学). Beijing: Science Press(北京： 科学出版社), 2003. 57.

[14] Ding R, Tsang L, Braunisch H. 2011 IEEE 20th Conference on Electrical Performance of Electronic Packaging and Systems (EPEPS), 2011. 161.

[15] Elson J M. JOSA A, 1995, 12(4): 729.

[16] ZHAN Yuan-ling, WANG Li(战元龄, 王 立). Acta Physica Sinica(物理学报), 1990, 39(2): 194.

[17] WANG Ling-mei, GAO Jun, XIE Zhao(王玲妹, 高 隽, 谢 昭). SCIENTIA SINICA Physica, Mechanica & Astronomica(中国科学： 物理学 力学 天文学), 2013, 43(7): 833.

[18] Thilak V, Voelz D G, Creusere C D. Applied Optics, 2007, 46(30): 7527.

*Corresponding author

欢迎投稿 欢迎订阅 欢迎刊登广告

Polarization Modeling and Analysis of Light Scattering Properties of Multilayer Films on Slightly Rough Substrate

CAO Hui, GAO Jun, WANG Ling-mei*, WANG Chi

Laboratory of Image Information Processing， Hefei University of Technology, Hefei 230009, China

To satisfy the demand of multilayer films on polarization detection, polarized bidirectional reflectance distribution function of multilayer films on slightly rough substrate is established on the basis of first-order vector perturbation theory and polarization transfer matrix. Due to the function, light scattering polarization properties are studied under multi-factor impacts of two typical targets-monolayer anti-reflection film and multilayer high-reflection films. The result shows that for monolayer anti-reflection film, observing positions have a great influence on the degree of polarization, for the left of the peak increased and right decreased compared with the substrate target. Film target and bare substrate can be distinguished by the degree of polarization in different observation angles. For multilayer high-reflection films, the degree of polarization is significantly associated with the number and optical thickness of layers at different wavelengths of incident light and scattering angles. With the increase of the layer number, the degree of polarization near the mirror reflection area decreases. It reveals that the calculated results coincide with the experimental data, which validates the correctness and rationality of the model. This paper provides a theoretical method for polarization detection of multilayer films target and reflection stealth technology.

Scattering; Multilayer films target; Polarized bidirectional reflectance distribution function; Degree of polarization; Mueller matrix

Sep. 26, 2014; accepted Jan. 22, 2015)

2014-09-26，

2015-01-22

国家自然科学基金项目(61271121)资助

曹 慧， 1990年生， 合肥工业大学硕士研究生 e-mail： caohui_liqun@126.com *通讯联系人 e-mail： wanglingmei@hfut.edu.cn

O436.3

A

10.3964/j.issn.1000-0593(2016)03-0640-08