基于双积分球的宽光谱组织光学参数测量系统与方法研究

韩 蕾，李晨曦,2*，孙承涛，蒋景英，赵会娟,2，徐可欣,2

1. 天津大学精密仪器与光电子工程学院，天津 300072 2. 天津大学精密测试技术及仪器国家重点实验室，天津 300072

基于双积分球的宽光谱组织光学参数测量系统与方法研究

韩 蕾1，李晨曦1,2*，孙承涛1，蒋景英1，赵会娟1,2，徐可欣1,2

1. 天津大学精密仪器与光电子工程学院，天津 300072 2. 天津大学精密测试技术及仪器国家重点实验室，天津 300072

组织光学参数测量是生物医学光子学的主要研究内容之一，人体组织光学性质与其生理病理状态密切相关。近年来，利用组织光学特性，特别是吸收与散射特性进行组织成像诊断及无创成分检测成为生物医学光子学领域研究热点，为肿瘤早期诊断、代谢动态监护及光动力治疗等临床应用提供了基础。双积分球方法能够同时测量离体组织吸收系数、散射系数等，具有测量准确、快速，适用范围大等优点，作为光学参数测量的标准方法得到广泛研究与应用。利用双积分球及超连续激光器搭建了宽光谱的组织光学参数测量系统，分析了积分球测量传递函数与误差来源及系统最佳测量条件，建立了基于BP-MCML的系统校正正向模型与L-M算法的光学参数反构算法。在此基础上，测量了1 100～1 400 nm连续宽谱范围内Intralipid溶液光学参数，实验结果表明改进后反构算法测量结果比较准确，多次测量标准偏差在3%以内，不同波长下约化散射系数及吸收系数测量结果与其他研究小组得到的测量结果对比，偏差小于3.4%。

双积分球； 组织光学参数； 参数校正； 多波长

引 言

组织光学参数是一系列描述光在组织中传播特性的参量，包括吸收系数、散射系数及各向异性因子等。测量方法根据原理可分为时域、频域、稳态径向距离分辨的在体测量方法，及采用积分球的离体测量方法[1-3]。双积分球测量方法通过测量样品的反射率及透射率，结合反构算法获取待测样品的吸收、散射系数等光学参数。该方法测量准确，应用范围广泛，被视为组织光学参数测量领域的金标准[4]。国内外很多研究小组进行了双积分球离体组织光学参数的测量研究，光源多采用HeNe或者分立LD激光器组合，波长范围小、分辨率差； 在参数反构算法中，对于系统测量误差及校正研究较少。在生物医学光子学中，常需要测量组织在宽光谱连续波长的光学参数，对系统及反构算法精度与适用范围要求较高。

本文构建了基于双积分球测量原理的连续波长组织光学参数测量系统，利用超连续谱激光器及高分辨率光谱仪实现1 100～1 400 nm范围内连续波长吸收系数及约化散射系数的测量。利用蒙特卡洛方法分析了测量过程中侧漏及串扰等对于测量结果的影响，研究了系统测量误差校正方法及最佳测量条件，提出了反向传播神经网络-蒙特卡洛(back propagation neural network-Monte Carlo multi-layered tissues，BPNN-MCML)与L-M算法(Levenberg-Marquardt算法)相结合的光学参数反构算法。本文研究的双积分球测量系统克服了分立波长系统波长范围窄、测量时间长、不同波长激光器性能差异造成测量结果误差大等缺点，采用改进的反构算法，进行系统误差校正，减少了测量误差对于光学参数反构结果的影响，具有测量准确、速度快、波长范围大等优点。

1 测量方法与系统构成

1.1 双积分球测量原理

双积分球是利用相对测量获取样品反射率、透射率的方法[4-5]，原理如图1。

(1)如图1(a)所示，盖住反、透射球的出、入射窗，测量暗噪声Rd-1，Td-1。

(2)如图1(b)和(c)所示，将标准反射板放置在反射球、透射球的出窗口，测量反射率为rstd的反射板反射值Rd-ref及空气(T=100%)透射值Td-ref。

(3)如图1(d)所示，将待测样品置于两个积分球之间，测量其反射值及透射值为Rd-s，Td-s，则样品的反射率及漫透射率为

(1)

(2)

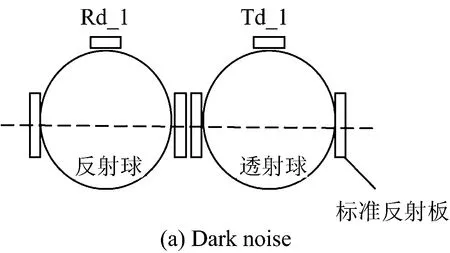
Fig.1 Schematic diagram of the double integrating spheres

1.2 系统组成

本文研究的连续宽光谱双积分球测量系统结构如图2所示：

Fig.2 Schematic diagram of system

(1)光源采用超连续谱光纤激光器(YSL-1040-01，武汉安扬激光技术有限责任公司)； 输出波长460～2 000 nm； 输出功率500 mW以上。

(2)积分球(IS-60-IG，Labsphere.Inc)直径6英寸, Infragold涂层, 1 100～1 700 nm波长下反射率≥0.935。

(3)1×4多模光开关(FSW 1×4-MM-C，中国电子科技集团公司第三十四研究所)工作波长范围1 100～1 700 nm； 平均插损≤3.5 dB。

(4)光谱仪(NIRQuest512，OceanOptics.Inc)测量范围900～1 700 nm； 信噪比>15 000∶1，波长分辨率1.6 nm。

(5)样品池，两片石英玻璃夹持样品仓的Sandwich结构，可适应不同厚度固态或液态样品测量需要。

(6)系统控制及数据采集基于美国NI公司LabVIEW环境自主开发，实现光开关采集通道切换、光谱仪参数设置、数据采集、存储、预处理等功能。

2 双积分球测量误差分析

双积分球测量误差主要来源包括积分球收集光口侧漏，两球间串扰及样品、标准反射板与积分球内涂层反射率差异造成光分布不均匀[5-6]。如图3所示，样品池的厚度对积分球侧漏光损失的大小有一定的影响。

Fig.3 Diagram of the light loss

分析不同样品厚度及光学参数下，系统测量光损失，如图4所示。当光学参数值较小时，样品池厚度较小的两组光损失较大。当吸收系数一定时，1.0 mm与1.3 mm相比，随着约化散射系数的减小，光损失增大较为缓慢。因此实验中采用厚度为1 mm的样品池。

Fig.4 Diagram of light loss with the μa，change of different thickness

光在积分球内壁多次反射，理想状态下会在球体内形成均匀的光强，但是由于测量参考和待测样品反射率与积分球内涂层材料反射率不同，不同表面积光强差异会造成实际测量误差。分别用参量A表示反射面积，r表示反射率，F表示面积分数(即某部分面积与积分球内表面积之比)，L为某一表面上反射的光能量大小，E0表示照射到样品的初始光强。不同下标代表的含义分别为： i表示入射窗口，o表示出射窗口，s表示样品，d表示检测器，st表示标准反射板，1表示反射球，2表示透射球[7]。则积分球内具有不同反射率的内表面之间关系可表示为

A0=A-Ad-Ai-Ao

(3)

A0定义为积分球的有效内表面积，积分球内光强分布公式表示为

(4)

同样，对于透射球而言，表示为

(5)

测量中光从反射球(透射球)内透过样品进入到透射球(反射球)的现象为“串扰”[5-7]。根据积分球参数得到积分球测量传递函数如下

(6)

3 光学参数反构算法

3.1 正向模型研究

将双积分球系统测量所得样品漫反射及透射率，输入反构算法即可获取光学参数。本文研究的反构算法为基于BP-MCML的正向模型及L-M迭代逼近算法。

正向模型流程图如图5，首先根据研究波段范围内人体组织光学参数确定正向模型训练集。约化散射系数： 0～30 mm-1，间隔0.2 mm-1； 吸收系数： 0～8 mm-1，间隔为0.2 mm-1，且在0～0.15 mm-1区间细化为间隔0.01 mm-1。通过CUDAMCML[8]程序计算得到样品的R，T，Rra，Tra等。根据公式(3)-(6)及测量系统中积分球参数，得到虚拟积分球测量值(Rsim，Tsim)。将Rsim和Tsim与初始光学参数作为训练模型，对BPNN进行训练，当全局误差最小时，结束训练过程，并将训练好的BPNN模型作为本研究中的正向模型。本文采用的BP-MCML正向模型，结合了Monte-Carlo方法准确灵活及神经网络非线性建模速度快的优点，适用光学参数范围广[9-12]。

Fig.5 Flow chart of the establishment of forward model

3.2 L-M迭代逼近算法

(7)

迭代参数修正公式为

(8)

式中，dk为步长，I为单位矩阵，λ为正的常数。本文中所采用的改进型L-M算法，基于信赖域全局收敛原理，根据逼近效果调节补偿，改变L-M算法的收敛速率。当目标函数下降满足一定条件时λ减小，否则λ增大。反构算法流程如图6。

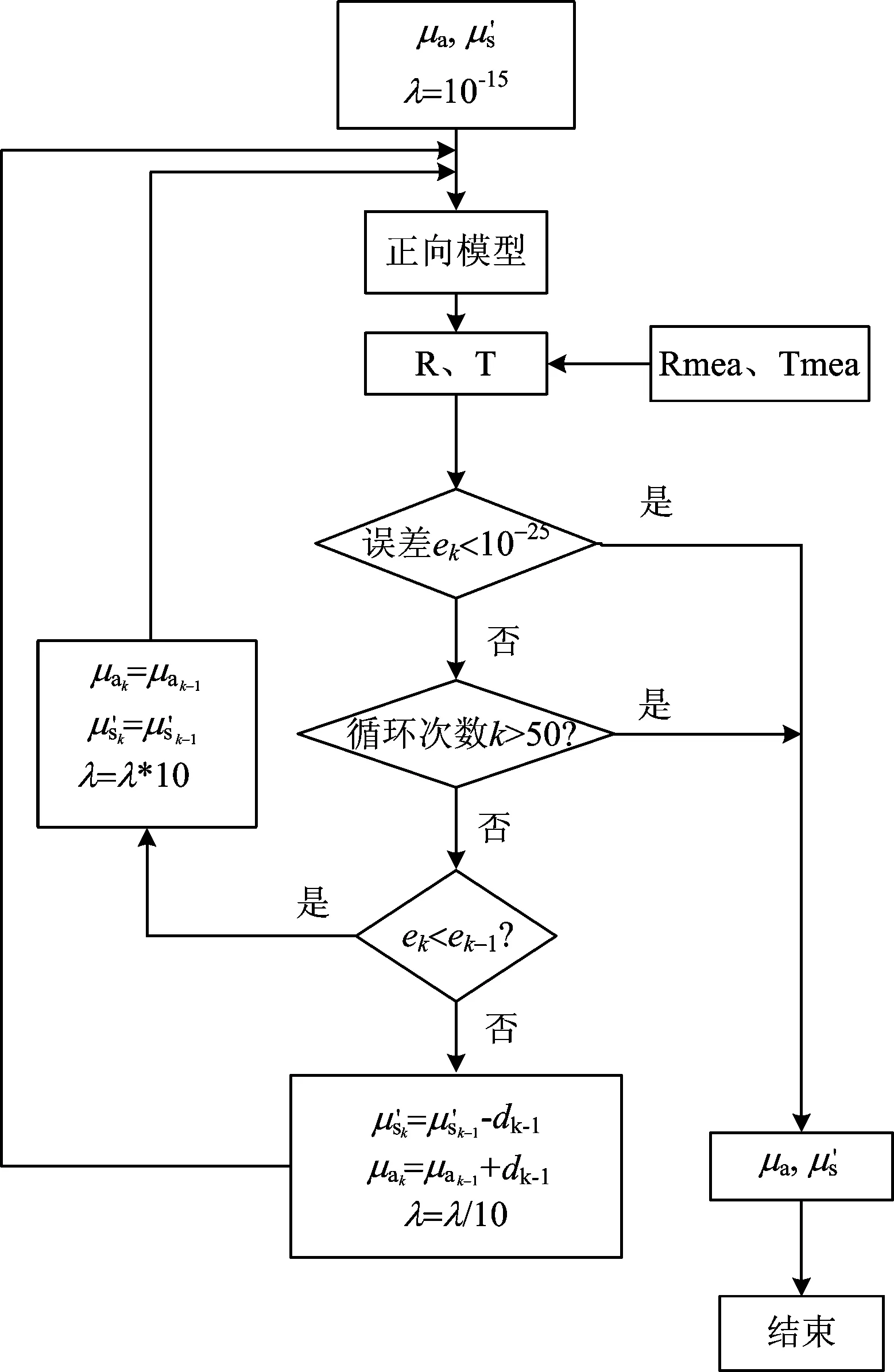
Fig.6 Flow chart of the L-M algorithm

4 结果与讨论

4.1 正向模型验证

为验证BP-MCML正向模型准确性，随机产生了25组光学参数，分别将其代入CUDAMCML模拟与BP-MCML模拟，将两种方法得到样品反射率及透射率结果相比较，如图7所示。

Fig.7 Results of the forward model validation

数据分析结果表明，25组数据的R和T平均相对误差分别为1.16%和1.89%。表明正向模型较为准确，且与蒙特卡洛模拟一致性较好。运算时间比蒙特卡洛模拟得到了明显改善，减少两个数量级，增加了程序的可执行性及实用性。

4.2 组织模拟液测量结果

Intralipid溶液具有光学性质稳定，散射特性与人体组织接近等优点，常作为标准散射溶液及光学仿体材料。本研究在双积分球测量系统及反构算法基础上，分别测量Intralipid-20%(华瑞制药有限公司)溶液在1 100～1 400 nm范围内吸收系数与约化散射系数。实验中将Intralipid与水体积配比1∶1的溶液，分别测量7次，测量结果平均值及标准差如图8所示。

在1 100～1 400 nm范围下，Intraliqid溶液中水为主要吸收介质，将10%Intralipid中水的吸收系数作为参考值，与测得的溶液吸收系数作对比，如图9所示，结果表明全波长范围内吸收系数的平均相对误差为8.21%，测量准确度较高，测量值与参考值的差异主要是由溶液中其他成分干扰造成，此外溶液散射系数较大，多次散射光程改变对吸收系数测量造成一定影响。

Fig.8 The measuring results of μa，of 10% Intralipid

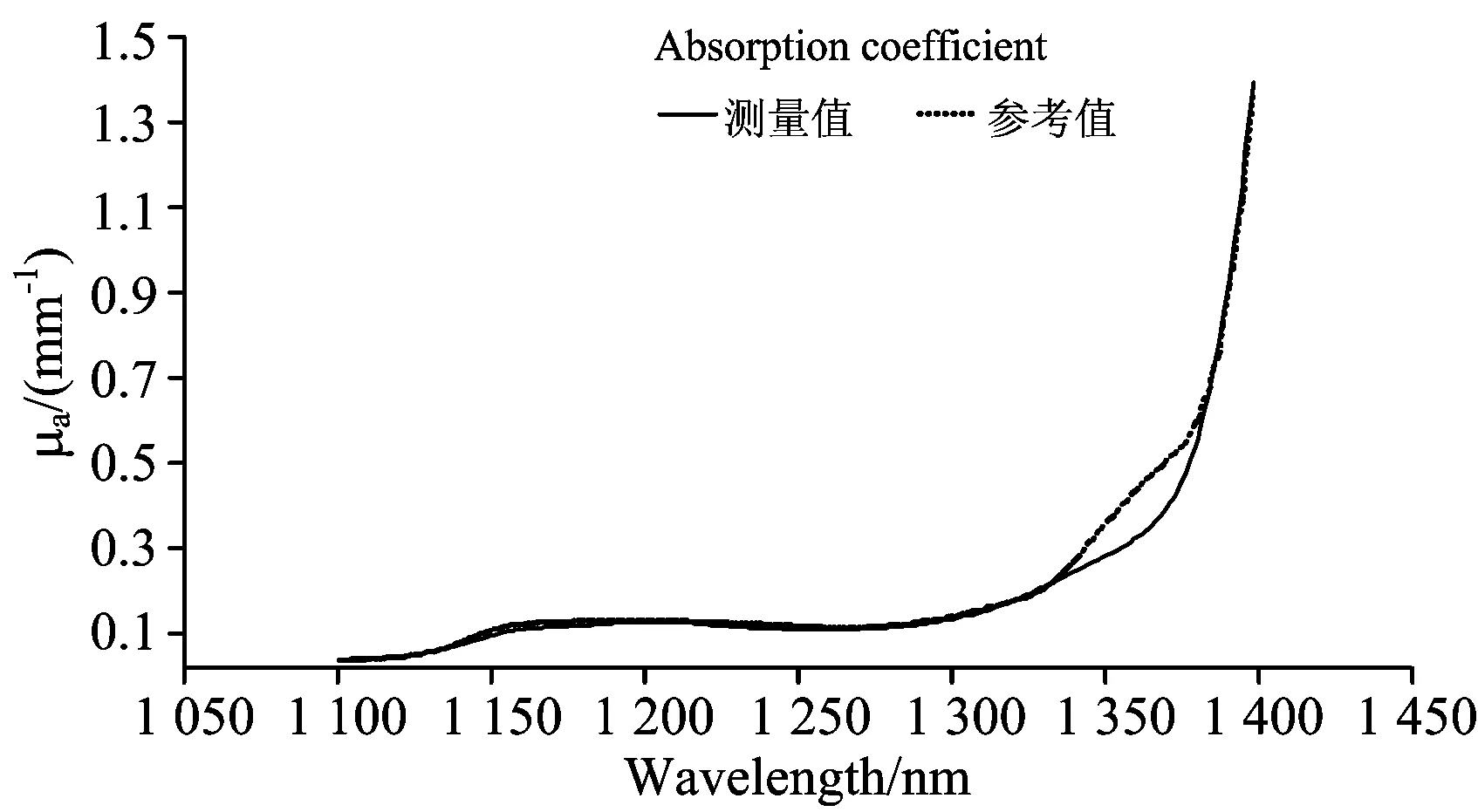
Fig.9 Results of the measurement of μa

根据系统测量到的1 100～1 400 nm范围内不同浓度下Intralipid溶液的约化散射系数，针对每个波长进行拟合，得到公式为

(9)

其中c为浓度分数，式中aλ表示体积比系数。拟合结果表明，不同波长下散射系数与浓度的相关性系数在0.995 1～0.999 8之间，表明实验所用Intralipid溶液的约化散射系数与浓度之间成线性关系，这与其他小组研究结果吻合。

根据Mie散射原理，在粒径一定的情况下，随着波长变大，散射系数变小，将测量得到的约化散射系数与波长之间进行非线性拟合，得到1 100～1 400 nm范围内Intralipid-20%溶液的约化散射系数拟合曲线，拟合结果如式(10)，相关系数达0.980 1。

(10)

如图10所示，本文测量结果与Chen[14]等文献中所述Intralipid-20%约化散射系数较为接近，1 100～1 400 nm波长范围内的平均相对误差为3.38%。误差的可能原因是Intralipid生产厂家及产品批次不同，散射颗粒物粒径及分布具有一定差异。

Fig.10 Results of the measurement of

5 结 论

利用双积分球、超连续谱激光器及高分辨率光谱仪构建了连续宽谱组织光学参数测量系统，实现了1 100～1 400 nm连续波长生物组织吸收系数及约化散射系数测量，分辨率达到1.6 nm。研究了双积分球测量的误差来源、校正方法及最佳测量条件，提出了BPNN-MCML与L-M算法相结合的反构算法。测量仿体溶液Intralipid的吸收系数及约化散射系数，多次测量标准偏差在3%以内，不同波长下光学参数测量结果与其他研究小组对比，偏差小于3.4%。本文研究的双积分球测量系统具有测量波长范围宽，波长分辨率好，测量准确快速等优点，可应用于人体组织的光学参数测量。

[1] Moritz Friebel, Jürgen Helfmann, et al. Journal of Biomedical Optics, 2009, 14(3)： 034001.

[2] Wang Yanqiu, Lin Ling, et al. Optical Technique, 2001, 27(4): 355.

[3] Tamara L Troy, Suresh N Thennadil. Journal of Biomedical Optics, 2001, 6(2): 167.

[4] Xu Kexin, et al. Biomedical Photonics. Beijing: Science Press, 2007.

[5] Wang Qiuyin. Investigations on the Improvement of Double-Integrating-Spheres System for Measuring Tissue Optical Properties. Tianjin: College of Precision Instrument and Electronic Engineering, Tianjin University, 2010.

[6] de Vries G, Beek J F, et al. IEEE Journal of Selected Topics in Quantum Electronics, 1999, 5(4): 944.

[7] Zhu Dan, Lu Wei, et al. Journal of Biomedical Optics, 2007, 12(6)： 064004.

[8] Erik Alerstam, et al. Journal of Biomedical Optics, 2008, 13(6): 060504.

[9] Guan Tangbing. A Study on Reconstruction of Tissue Optical Properties Based on Monte Carlo Propagation Model. Tianjin: College of Precision Instrument and Electronic Engineering, Tianjin University, 2007.

[10] Wang Lihong, et al. Computer Methods and Programs in Biomedicine, 1995, 47: 131.

[11] Li Chenxi, Zhao Huijuan, et al. Chinese Optical Letters, 2010, 8(2): 173.

[12] MIAO Jing, CAO Yu-zhen, YANG Ren-jie, et al(苗 静，曹玉珍，杨仁杰，等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2013, 33(11): 3032.

[13] Yang Liu. Numerical methods for system of singular nonlinear equations and nonlinear least square problems. Xiangtan: Department of Mathematics, Xiangtan University, 2003.

[14] Chen C, et al. Optics Express, 2006, 14(16): 7420.

*Corresponding author

The Research on Measurement System and Method of Tissue Optical Parameters with Wide Spectra Based on Double-Integrating-Spheres

HAN Lei1，LI Chen-xi1, 2*，SUN Cheng-tao1，JIANG Jing-ying1，ZHAO Hui-juan1,2，XU Ke-xin1,2

1. College of Precision Instruments and Optoelectronics Engineering, Tianjin University, Tianjin 300072, China 2. State Key Laboratory of Precision Measuring Technology and Instruments, Tianjin University, Tianjin 300072, China

The measurement of tissue optical parameters is the focusing research content of Biomedical Photonics. The optical properties of human tissue are closely related to the physiological and pathological state. In recent years, the tissue imaging diagnosis and non-invasive detection of componentsbecome the hot research topics, applying the tissue optical properties especially the absorption and scattering properties. These provide the basis for the study of optical imaging and the spectrum detection of body composition etc. The Double-Integrating-Spheres (DIS) method can measure the absorption coefficient, scattering coefficient and so on in vitro tissuesimultaneously. It has the advantages of accurate, rapid, large applicable scope. The method applya standard method for measuring the optical parameters. This paper build the wide spectrum measurement system of optical parameters based on DIS and super continuum lasers. Then we analyze the transfer function, error sources and the best measuring conditions of the system. Finally we establish the correction forward model based on BP-MCML and the inverse algorithm of the optical parameters based on L-M algorithm. The optical parameters of intralipid solution in the wavelength range of 1 100～1 400 nm are measured. The experiment results show that the improved inverse algorithm is accurate. The multiple measurements standard deviation is within 3%. Compared the results of scattering coefficient and absorption coefficient at different wavelengths to the results of other research groups, the deviation is less than 3.4%.

Double-integrating-spheres; Tissue optical parameters; Parameter correction; Multi-wavelength

Oct. 18, 2014; accepted Feb. 1, 2015)

2014-10-18，

2015-02-01

国家自然科学基金项目(81401454，81471698)，国家(863)高技术研究发展计划项目(2012AA022602)，中国博士后科学基金项目(2013M541174)，中国博士后国际交流计划项目(20140066)资助

韩 蕾，女，1990年生，天津大学精密仪器与光电子工程学院硕士研究生 e-mail: hanlei9047@126.cpm *通讯联系人 e-mail: lichenxi@tju.edu.cn

O657.3

A

10.3964/j.issn.1000-0593(2016)02-0561-06