LIBS对煤中热值检测的新型校正模型
王 帝, 陆继东*, 董美蓉, 姚顺春, 樊 炬, 田照华, 王 磊, 李诗诗
1. 华南理工大学电力学院, 广东 广州 510640
2. 广东省能源高效清洁利用重点实验室, 广东 广州 510640
LIBS对煤中热值检测的新型校正模型
王 帝1, 2, 陆继东1, 2*, 董美蓉1, 2, 姚顺春1, 2, 樊 炬1, 2, 田照华1, 2, 王 磊1, 李诗诗1, 2
1. 华南理工大学电力学院, 广东 广州 510640
2. 广东省能源高效清洁利用重点实验室, 广东 广州 510640
将激光诱导击穿光谱技术(LIBS)应用于煤中热值的检测。 针对传统的通道面积归一化方法未能考虑煤质检测的物理/化学机制、 从而限制了所建模型在精确性、 准确性、 可重复性的情况, 提出了一种新型的基于光谱偏差产生原理的校正模型。 模型选取了19组煤样品, 随机选择其中15组为校正集, 用于建立热值的定量分析模型, 剩余四种为预测集, 用于对所建模型进行检验与评价。 模型从光谱偏差因素的产生因素出发, 通过原子光谱发射理论结合斯塔克展宽公式, 推导出LIBS条件下自吸收效应的影响机制及其所引起的偏差的修正方法。 通过元素间相互干扰结合基体效应的微观机理对基体效应进行光谱的偏差分析, 并根据K系数法的思路对LIBS中元素间相互干扰进行修正, 通过建立光谱的电子密度, 等离子体温度, 元素浓度的数值模型对基体效应引起的光谱偏差进行深度修正。 因而经过自吸收效应—元素间相互干扰—基体效应深度修正后, 模型对于所研究样品范围内其拟合优度R2=0.967, RMSEP=0.49 MJ·kg-1, RMSE=0.45 MJ·kg-1, MRE=2.42%, ARE=1.64%的同时RSD=5.79%, RSDP=8.10%。 相对于传统的通道面积归一化-多元线性回归方法的0.405, 8.28 MJ·kg-1, 4.14 MJ·kg-1, 22.85%, 52.48%, 18.28%, 32.85%, 表明测量的精确度与准确度都得到明显的提高, 证明该模型具有很好的应用价值。
LIBS; 热值; 自吸收效应; 元素间相互干扰; 基体效应
引 言
激光诱导击穿光谱技术(LIBS)是一种在强脉冲激光作用下, 分析样品被瞬间电离形成高温等离子体, 通过解析等离子体冷却过程中的发射光谱信息, 实现元素种类和浓度分析的典型的原子发射光谱技术。 相对传统的光学测量方法, LIBS技术因不需要或者仅仅只需要进行简单的预处理、 对样品基本没有损害和多种元素同步、 快速检测的优势, 正在逐步发展成为一种极具竞争力的工业过程在线检测技术, 目前正在尝试应用于各种工业过程的质量控制或状态诊断, 包括矿产[1]、 冶金[2]等行业。
国内外研究者所关注的研究热点主要是提高复杂物质组分分析准确度、 精确度为目的的定量分析方法。 Clegg等[3]利用包含特定元素信息的波段光谱根据偏最小二乘法(PLS)建立定标模型, 对岩石中所含的Si, Al, Fe和Mn等元素进行了定量分析。 Death等[4]将主成分回归方法应用于铁矿石中Fe, Al, Si, Mn, K和P的定量分析, 利用特定波段内的所有谱线与分析对象含量建立对应关系, 得到良好的定量分析结果。
在煤质检测的研究方面, Zhang等[5]采用内标法对煤中有机氧含量进行测量, 由于煤的高度复杂性, 预测误差为19.39%。 尹王保等通过筛选数据、 归一化、 积分等手段对煤中碳元素含量进行检测, 使得预测误差在1.6%以内。 Wang等[6]为了提高煤质成分的定量分析准确度, 提出了一种主导因素和偏最小二乘法相结合的定量分析方法, 其结果优于传统的PLS模型, 结合Li等提出的标准归一化模型[7]时, 其结果的精确度和准确度进一步得到提高。 除了应用LIBS实现煤的元素分析以外, 国内外学者也尝试利用LIBS实现煤质的工业分析。 谢承利等[8]通过多元线性回归模型检测煤质中的灰分, 其定量分析的相对误差在1%~8%之间。 姚顺春等[9]通过PLS建立多元线性回归模型对灰分进行测量, 预测的相对误差进一步减小。 董美蓉等[10]通过偏相关分析和主成分分析相结合的方式研究煤质中的挥发分, 建立的模型具有较高的拟合优度与预测能力。 Yuan等[11]通过非线性主导因素的PLS模型对煤中的热值进行了分析, 相对于传统PLS模型, 该模型的平均预测误差(ARE)从3.55%降低到2.71%。 本文选用煤质特性存在差异的煤样, 进行LIBS实验, 结合煤质本身的物理化学特性, 提出一种新型校正模型, 以提高采用LIBS进行煤中热值分析的精确度和准确度。
1 实验部分
采用的LIBS检测系统, 详见文献[12-13], 选用调Q脉冲Nd∶YAG固体脉冲激光(Quantel激光器), 工作波长为1 064 nm, 脉宽6 ns, 激光能量为41.1 mJ, 能量波动范围在0.75%以内。 经准直透镜收集的光谱信号经过光纤传送到波长范围175~1 075 nm、 分辨率为0.05~0.13 nm、 最小积分时间为2 ms的8通道光谱仪(AvaSpec-2048FT-8-RM)。 焦距设置在表面以下2 mm处。 延迟时间为424 ns。
实验选取了19组煤样品, 随机选择其中15组为校正集, 用于建立热值的定量分析模型。 剩余四种为预测集, 用于对建立的模型进行检验与评价。 所选取的煤样(空气干燥基)的元素分析和热值分析结果如表1所示。

表1 实验所选煤样
2 模型建立
煤中的热值是反映煤质特性的一个最为重要的指标, 它与煤在燃烧过程中参与释放热量的化学反应各元素浓度相关。 其中煤中C, H, O的含量与热值的大小息息相关, 因此考虑将C, H, O三个元素的谱线强度作为建立热值定量分析模型的主要因素, 建立如式(1)的表达式
Q=k1IC+k2IH+k3IO+k4
(1)
式(1)中Q为热值,k1,k2,k3为热值关于C, H, O三种元素的光谱强度IC,IH,IO的多元线性回归的拟合系数。k4在物理意义上为归一化后的光谱残差, 用于进行后续的残差修正。
2.1 传统通道面积归一化模型
在光谱测量过程中, 由于测量环境、 设备稳定性、 信号干扰等主客观原因的存在, 常常导致得到的光谱数据绝对值强度差别较大, 为了便于比较不同条件下的测量结果, 往往需要对光谱曲线进行归一化处理[14]。 通道面积归一化方法是比较常见的一种光谱预处理方法, 其处理方法如式(2)
(2)
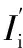
2.2 新型校正模型
激光与物质作用产生的等离子体发射光谱中还存在元素发射谱线的自吸收效应、 元素间的相互干扰和基体效应, 致使采集得到的光谱数据波动较大, 这也是影响LIBS测量准确度的重要原因。 考虑从上述三个因素对光谱数据逐步进行修正后建立回归模型。
2.2.1 自吸收影响的消除
根据原子发射光谱理论, 经过推导可以得到考虑自吸收效应和不考虑自吸收的光谱强度之间的关系, 见式(3)
(3)
假设式(3)的结果为自吸收系数SA(self-absorption), 根据理论推导和拟合, 见式(4)
(4)
对于某个元素, 根据斯塔克展宽公式Δλ0=2wsne, 因而得到式(5)
(5)
式(5)中,ne为电子密度, 可由不受自吸收效应影响的Hα(656 nm)计算得到, Δλ由谱线的Lorentzian拟合曲线的半高宽近似,ws为斯塔克半宽参数, 可以查阅文献[15-17]。
计算出自吸收系数SA后, 代入有自吸收和无自吸收的光谱强度关系式(3)中, 即可对自吸收对光谱的影响进行一定程度的消除。
2.2.2 基体效应的修正
样品本身基体的物理/化学特性对等离子体光谱数据的影响称为基体效应[18-19]。 煤作为一种由多元素多组分多结构组成的复杂物质, 不仅有元素间的相互干扰, 还存在由电子密度、 元素浓度和等离子体温度等变化引起的基体效应[20]。 因而考虑先从元素间相互干扰进行对基体效应的初步修正, 然后再从等离子体的作用机制上对基体效应进行深度修正。
2.2.2.1 元素间相互干扰的修正
对于煤样这种复杂体系的样品, 内部往往含有多种元素(主量元素、 次量元素和微量元素), 因此元素之间的相互影响不可避免。 而LIBS测量中直接探测到的是光谱强度, 利用元素浓度与谱线强度间线性拟合关系式I=kc, 结合K系数法的修正思路, 得到如下考虑光谱二次干扰的光谱数据建立的校正关系式, 如式(6)所示
(6)
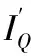
在建立定标模型时, 由于校正集样品数目有限, 且煤质的LIBS光谱中存在大量的光谱信息, 包括原子、 离子、 分子谱线。 如果直接选取所有元素的谱线进行拟合修正, 必然会由于变量数目大于样本数而导致过拟合现象。 Na, Mg, Al和Si是煤中灰分的主要元素, 这几个元素不仅化合价态不同, 且各元素的电离能差别较大, 具有一定的代表性, 因而选作被修正的干扰元素。
2.2.2.2 基体效应的深度消除
Li等[21]在对Cu合金进行LIBS检测时, 提出的光谱简化标准化方法, 是在假定的标准等离子体状态下, 对光谱强度进行泰勒展开, 并根据在作用机制上光谱强度的基体效应影响因素为电子密度、 元素浓度和等离子体温度。 对这三种因素分别进行线性偏差拟合, 成功提高了模型各方面的性能。 但是由于其是基于泰勒展开式, 致使对实际光谱的线性度(即拟合优度)要求较高。 而煤由于其复杂的基体特性, 因而直接将该方法用来消除基体效应的影响存在一定的局限性。 同时该方法是针对单元素谱线进行归一化, 而热值是关于C, H和O等的多元素模型, 因而本研究提出了对该方法进行改进的模型。
Li等[8]提出的简化的标准化模型如式(7)
(7)
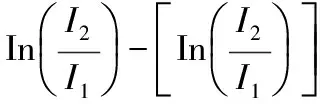
结合Wang等[22]的研究, 将经过去自吸收、 去元素间相互干扰的C″, H″, O″元素进行热值拟合的拟合值当做热值Q″ , 并将其作为单次测量所得的光谱强度的线性关联值。 利用C″2- CN″补偿C″原子谱线, 并且结合所有经过去自吸收与去元素间相互干扰校正后的C″, H″, O″原子谱线表示热值Q的总光谱强度偏差k2ITQ。I″2,I″2取经过去自吸收、 去元素间相互干扰的Si″元素的两条谱线强度。 根据斯塔克效应, 利用Hα″拟合谱线半高宽计算电子密度的变化。 因而改进后用于热值分析的模型为式(8)
(8)
同样, 以迭代算法算出最大拟合优度为目标, 建立收敛模型。
2.3 模型评价指标
对于多元线性定标模型, 可以从以下七个方面进行比较完整的评价。 首先是决定系数R2, 即模型在校正集内数据的拟合优度, 评价校正集模型的准确性; 其次是预测均方根误差RMSEP(root mean square error of prediction)和均方根误差RMSE(root mean square error), 从整体上评价模型的预测能力。 预测平均相对误差ARE(average relative error)和预测最大相对误差MRE(maximum relative error), 从单次测量上评价模型的预测能力。 最后是光谱谱线强度的相对标准偏差RSD(relative standard deviation)和预测相对标准偏差RSDP(relative standard deviation of prediction), 用于评价LIBS测量模型的精确度, 以及测量的重复性。
3 结果与讨论
根据煤的组成特点, 结合NIST标准数据库, 选择用于模型建立的特征谱线如表2所示。

表2 实验所选谱线
3.1 不同方法结果对比
经过传统的通道面积归一化-多元线性回归模型处理后得到的热值预测值与参考值之间的关系, 如图1所示。 针对复杂成分样品, 采用该模型虽然在一定程度上可以消除烧蚀量变化带来的影响, 但是对于煤这种复杂的样品, 对光谱的影响因素较多, 致使直接采用这种方法难以满足热值定量分析的要求。
图2, 图3和图4为依次经过自吸收效应修正、 元素间相互干扰修正和基体效应深度修正后建立的多元线性模型计算值与参考值之间的对比。 可见, 经过新型校正模型处理后, 拟合曲线的斜率越来越接近45°, 说明经过修正后模型的可靠性增加, 并且发现修正元素间相互干扰后, 模型的可靠性提升最大。 校正集的点逐渐靠近拟合曲线, 说明拟合优度逐步提升。 预测集的点逐步靠近拟合曲线, 说明模型的预测能力也在逐步提升。

图1 通道归一化后的计算热值与标准热值之间的关系
Fig.1 The relationship between calculated value and standard calorific value after channel normalization
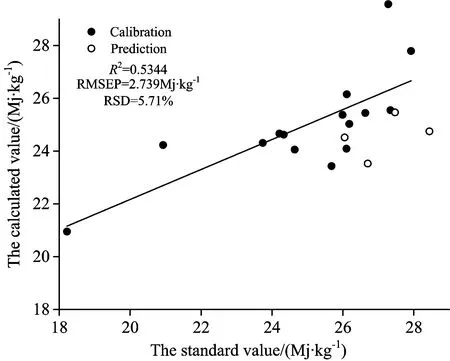
图2 经过自吸收处理后的热值与标准值之间的关系
Fig.2 The relationship between the calculated value and the standard value with self-absorption correlated
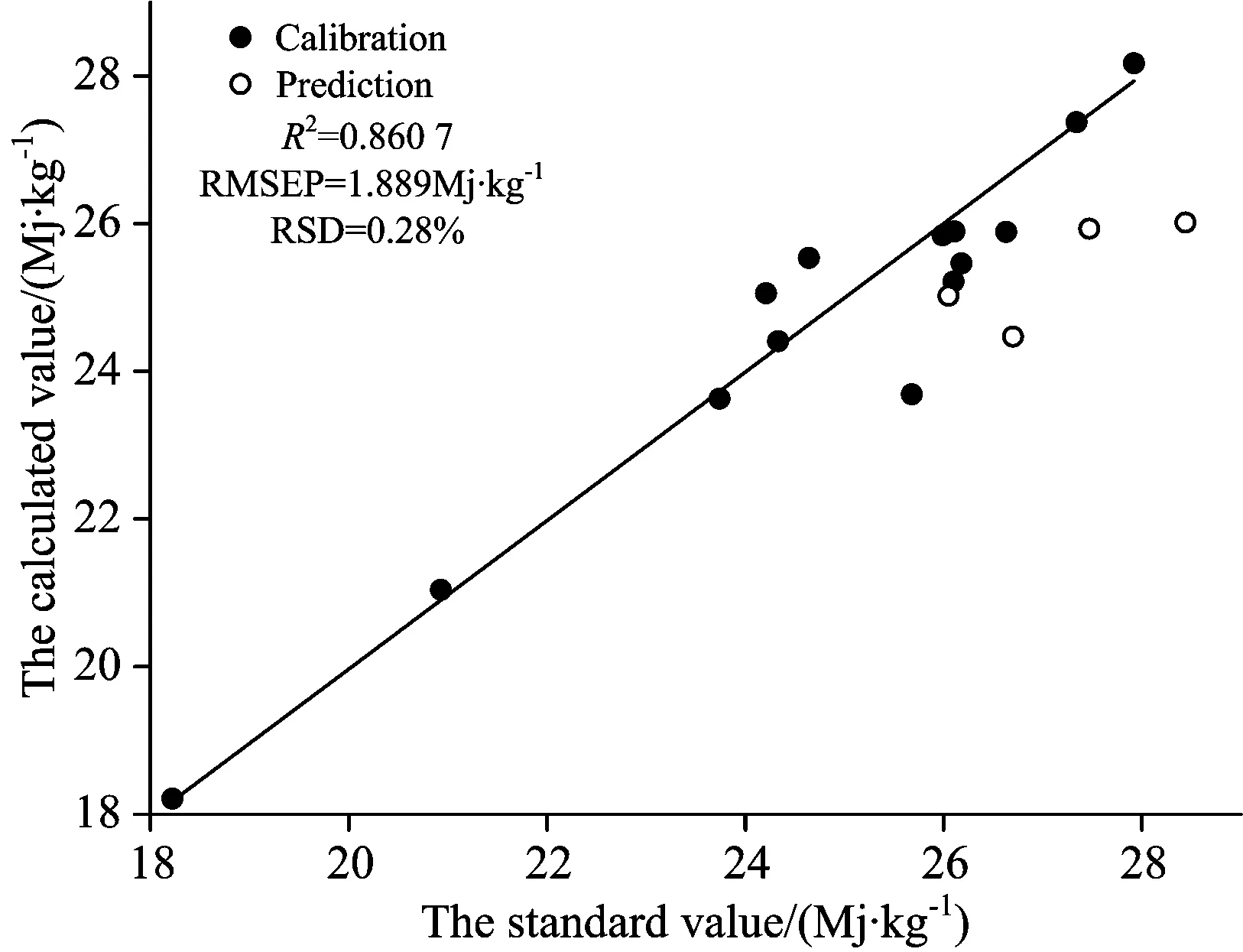
图3 经过元素间相互干扰处理后热值与标准值之间的关系
Fig.3 The relationship between the calculated value and the standard value with inter-elements interfere correlated
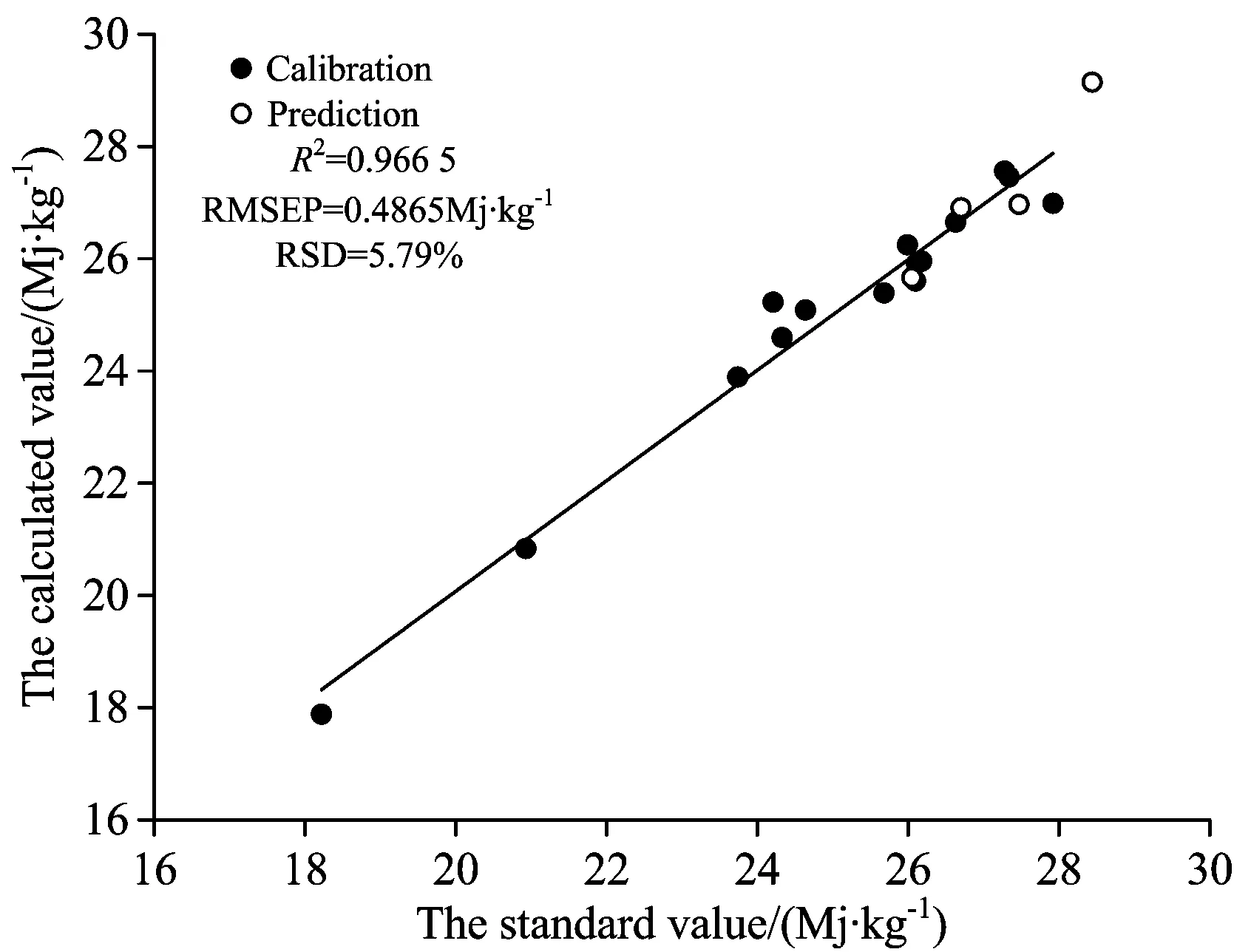
图4 经过基体效应深度处理后热值与标准值之间的关系
Fig.4 The relationship between the calculated value and the standard value with matrix effect correlated
3.2 实验结果评价
利用2.3中的各个评价指标的计算公式, 得到实验结果对比, 如表3所示。

表3 实验结果指标对比
经过自吸收效应—元素间相互干扰—基体效应修正后, 模型对于所研究样品范围内其拟合优度R2=0.967, 相比于传统方法的0.405, 说明模型的可靠性明显增强。 新型校正模型的RMSEP=0.49 MJ·kg-1, ARE=1.64%相比于传统方法的8.28 MJ·kg-1, 22.85%, 说明新模型的预测能力大幅提高。 同时新型校正模型的RSD=5.79%相对于传统方法的18.28%, 说明模型的可重复性能提高。 而新型校正模型的RSDP=8.10%相对于传统方法的32.85%, 表明测量的精确度得到明显的提高。
相比传统的通道面积归一化-多元线性回归模型, 新型校正模型在模型的可靠性、 预测能力以及模型的可重复性上均有极大的提高。 表明基于自吸收效应、 元素干扰、 基体深度效应修正的校正模型能较好地实现LIBS用于煤中热值的检测。
4 结 论
将LIBS技术运用于煤中热值的检测。 通过对19个煤样的离线元素分析和工业分析可知, 可以通过建立C, H, O的多元线性模型, 用于实现煤中热值定量分析模型的建立。 在此基础上, 根据影响LIBS测量煤样光谱的主要因素, 分别对自吸收效应、 元素间相互干扰、 基体效应进行光谱修正, 将修正后的光谱数据进行线性回归建模, 最后将模型用7个指标进行完整的评价。 结果表明, 相比传统的通道面积归一化-多元线性回归模型, 经过三种偏差因素修正后的新型校正模型在模型可靠程度、 预测能力以及模型的可重复性上均有明显的提高。
[1] Salle B, Lacour J L, Vors E. Spectrochimica Acta Part B, 2004, 59(9): 1413.
[2] Hemmerlin M, Meilland R, Falk H. Spectrochimica Acta Part B, 2001, 56(6): 661.
[3] Clegg S, Sklute M, Dyar E. Spectrochimica Acta Part B, 2009, 64(1): 79.
[4] Death D L, Cunningham A P, Pollard L J. Spectrochimica Acta Part B, 2008, 63(7): 763.
[5] Zhang Lei, Dong Lei, Dou Haipeng. Applied Spectroscopy, 2008, 62(4): 458.
[6] Li Xiongwei, Wang Zhe, Fu Yangting. Spectrochimica Acta Part B-Atomic Spectroscopy, 2014, 99(10): 82.
[7] Wang Zhe, Li Lizhi, West L. Spectrochimica Acta Part B-Atomic Spectroscopy, 2012, 68: 58.
[8] XIE Cheng-li, LU Ji-dong, LI Peng-yan(谢承利, 陆继东, 李鹏艳). Engineering Thermal Physics(工程热物理学报), 2009, 30(2): 329.
[9] Yao Shunchun, Lu Jidong, Dong Meirong. Applied Spcetroscopy, 2010, 65: 1197.
[10] Dong Meirong, Lu Jidong, Yao Shunchun. J. Anal. At. Spectrom., 2011, 26: 2183.
[11] Yuan Tingbi, Wang Zhe, Lui Siulung. J. Anal. At. Spectrom., 2013, 28(7): 1045.
[12] Yao Shunchun, Lu Jidong, Li Junyan. J. Anal. At. Spectrom., 2010, 25: 1733.
[13] Chen Kai, Lu Jidong. High Power Laser and Particle Beams, 2011, 23: 293.
[14] Body D, Chadwick B L. Spectrochimica Acta Part B-Atomic Spcetroscopy, 2001, 56(6): 725.
[15] Sherbini A M El, Hegazy H, Sherbini Th M El. Spectrochimica Acta Part B, 2006, 61: 532.
[16] Greim H R. Spectral Line Broadening by Plasmas, Academic, New York and London, Academic Press, 1974. 39.
[17] Hakkanen H, Houni J, Kaski S. Spectrochim. Acta Part B, 2001, 56: 737.
[18] Gaft M, Nagli L, Fasaki I. Spectrochimica Acta Part B-Atomic Spectroscopy, 2009, 64: 1098.
[19] Chadwick B L, Body D. Applied Spcetroscopy, 2002, 56(1): 70.
[20] Aguilera J A, Aragon C, Madurga V. Spectrochimica Acta Part B-Atomic Spectroscopy, 2009, 64(10): 993.
[21] Li Lizhi, Wang Zhe, Yuan Tingbi. Journal of Analytical Atomic Spectrometry, 2011, 26(11): 2274.
[22] Li Xiongwei, Wang Zhe, Fu Yangting. Spectrochimica Acta Part B-Atomic Spectroscopy, 2014, 99: 82.
*Corresponding author
A New Calibrated Model of Coal Calorific Value Detection with LIBS
WANG Di1, 2, LU Ji-dong1, 2*, DONG Mei-rong1, 2, YAO Shun-chun1, 2, FAN Ju1, 2, TIAN Zhao-hua1, 2, WANG Lei1,LI Shi-shi1, 2
1. School of Electric Power of South China University of Technology, Guangzhou 510640, China
2. Guangdong Province Key Laboratory of Efficient and Clean Energy Utilization, Guangzhou 510640, China
A set of coal samples were used for laser-induced breakdown spectroscopy (LIBS) experiment to measure the coal calorific value. Traditional channel normalization method didn't consider the physical / chemical mechanism of coal, which would limit the model in precision, accuracy and repeatability. Thus a new calibrated model based on the kinds of the effects of spectral deviation was proposed in this paper. The model selected 19 groups of coal samples, where the random 15 groups were used to establish quantitative analysis model of calorific value while the remaining four for inspection and evaluation. The model based on spectral deviation factors, and the transmission theory combined with the stark broadening formula was used to deduce the absorption effect mechanism and the deviation correction method under the condition of LIBS. The mutual interference between elements and the mechanism of matrix effect were being analyzed while K coefficient method was used to correct mutual interference between the elements in the LIBS. The establishment of numerical model with the electron density, the plasma temperature and the element concentration was used to deeply corrected spectrum deviation caused by matrix effect. Thus taking into consideration of the effect of self-absorption, interfere of inter-elements and matrix effect, the calibration model was established, whileR2=0.967, RMSEP=0.49 MJ·kg-1, RMSE=0.45 MJ·kg-1, MRE=2.42%, ARE=1.64%, RSD=5.79% and RSDP=8.10%. Compared with the 0.405, 8.28 MJ·kg-1, 4.14 MJ·kg-1, 22.85%, 52.48%, 18.28% and 32.85% of traditional channel normalized-multiple linear regression method, it demonstrated that the precision and accuracy have been improved significantly and model has good application value.
LIBS; Calorific value; Self-absorption; Inter-elements interference; Matrix effect
May 31, 2015; accepted Nov. 26, 2015)
2015-05-31,
2015-11-26
国家自然科学基金项目(51476061, 51406059), 煤燃烧国家重点实验室开放基金项目(FSKLCCA1509), 中央高校基本科研业务费专项资金(华南理工大学) 项目(2015ZM002)资助
王 帝, 1992年生, 华南理工大学电力学院硕士研究生 e-mail: 413222454@qq.com *通讯联系人 e-mail: jdlu@scut.edu.cn
TK16
A
10.3964/j.issn.1000-0593(2016)08-2607-06

