基于高光谱的鸡蛋新鲜度检测
王巧华, 周 凯, 吴兰兰, 王彩云
1. 华中农业大学工学院, 湖北 武汉 430070
2. 国家蛋品加工技术研发分中心, 华中农业大学, 湖北 武汉 430070
基于高光谱的鸡蛋新鲜度检测
王巧华1, 2, 周 凯1, 吴兰兰1, 王彩云1
1. 华中农业大学工学院, 湖北 武汉 430070
2. 国家蛋品加工技术研发分中心, 华中农业大学, 湖北 武汉 430070
借助高光谱成像仪采集贮期白壳鸡蛋的透射高光谱数据, 对比测量常规表征新鲜度的哈夫单位值, 用Matrix Laboratory (MATLAB)和Statistical Analysis System (SAS)等软件, 同时结合化学计量法对样品鸡蛋的高光谱数据进行分析处理, 建立了基于高光谱技术的鸡蛋新鲜度预测模型。 选用高光谱500~1 000 nm的波段作为敏感波段进行研究, 用马氏距离剔除鸡蛋异常样本数据, 并对鸡蛋高光谱数据进行了微分校正, 通过比较发现高光谱二阶微分与鸡蛋哈夫单位值之间的线性度高, 因此选用高光谱二阶微分数据来进一步研究, 并对其进行了小波去噪、 光滑处理及标准化处理。 选用近年新提出来的competitive adaptive reweighted sampling (CARS)变量选取法对高光谱进行降维, 提取出32个特征参数, 建立了白壳蛋基于全波段的偏最小二乘法(partial least square, PLS)预测模型和基于特征参数的多元回归模型, 验证集的相关系数分别为0.88, 0.93, 均方误差分别为7.565, 6.44。 用验证集的蛋对基于高光谱二阶微分全波段的偏最小二乘法预测模型、 基于特征参数的多元回归模型分别进行验证, 两个模型判别白壳蛋新鲜和不新鲜的最高准确率达100%, 88%。
鸡蛋; 新鲜度; 高光谱; 偏最小二乘法; 竞争性自适应重加权算法
引 言
一直以来, 涉及贮藏鸡蛋品质的评价、 预测及其与贮藏条件关系的研究一直是食品加工和保鲜领域关注热点问题之一。 生化方法存在检测周期长、 程序复杂等弊端, 且是破坏性检测, 不能满足现代检测要求。 常见的鸡蛋内部品质无损检测有机器视觉法[1-2]、 近红外检测法[3]和高光谱检测法[4-5]。 Mahmoud等[6]利用机器视觉系统采集鸡蛋图像信息, 用人工神经网络分别建立了哈夫单位、 蛋黄指数、 蛋黄蛋白重量比和蛋黄重的预测模型; 侯卓成等用近红外光谱仪采集鸡蛋光谱, 分别确定了鸡蛋蛋白高度、 气室直径和高度的预测模型。
采用机器视觉技术可以鉴别鸡蛋新鲜度, 但存在以下问题: 壳色、 厚度及光源亮度均对检测有影响, 而在建模时需要提取非常完整的图像特征参数, 故对图像采集的硬件及处理软件要求较高; 利用近红外光谱技术也可以检测鸡蛋新鲜度, 但存在数据分析工作量非常大, 且极易受到外部环境的影响, 在线动态检测时可以将这些影响放大, 要保证其具有比较稳定的测量范围非常困难, 因此应用于智能化检测还存在一定的难度。
由于高光谱成像技术是一种多信息融合技术, 采集到的数据信息中, 既含图像信息又含光谱信息, 有学者也已经将高光谱成像技术用于研究鸡蛋品质, 但基本都集中于孵化蛋和血斑蛋, Wei等[7]采集了种蛋前5天的高光谱数据, 提取图像的形态学特征参数, 并选取822 nm处的变量作为光谱的特征参数, 分别用图像形态特征参数和光谱特征参数建立种蛋孵化情况模型, 比较发现, 基于形态学的模型识别准确率较高。 目前还没有用高光谱检测普通鸡蛋新鲜度的研究报道, 本研究提出了基于高光谱的光学技术来检测鸡蛋新鲜度。
1 实验部分
1.1 材料
试验样本为165枚1日龄的白壳罗曼蛋, 购买于湖北武汉九峰鸡场。 所有鸡蛋置于24 ℃的生化培养箱中贮藏。
1.2 仪器
样品鸡蛋的高光谱数据采集是由高光谱成像系统(Hypersis-VNIR-CL, 卓立汉光, 美国)完成, 系统由高光谱成像仪、 计算机、 透射光源箱和高光谱采集软件(SpectraSENS) 等组成。 其中高光谱成像仪由光源、 开关、 Charge Coupled Device (CCD)相机和丝杠式移动平台等部分组成。 设置光谱波长范围为300~1 100 nm, 相机曝光时间设为0.1秒, 丝杠移动平台移动速度设置为1.7 mm·s-1, 移动距离设置为75 mm。
试验中对比测量鸡蛋重量用电子天平(JA2002, 上海浦春计量仪器有限公司, 上海), 蛋白高度由游标卡尺来测量。
1.3 光谱相机校正
由于CCD中光电转换芯片的材料和物理特性以及传感器内部杂质因热激发产生而影响图片质量的电子, 对图片来说这种电子属于噪声, 又称暗电流。 暗电流会影响高光谱图片质量, 因此在采集前需要用白板消除相机暗电流的影响。 消除暗电流的相机黑白校正公式为[8]
(1)
式(1)中,R为校正后光谱图像文件;R0为原始光谱图像文件;Rd为黑图像文件;Rw为白图像文件。
1.4 试验步骤
(1)贮存0, 3, 6, 9, 12, 15, 18, 21, 24和27 d时, 随机挑出15枚蛋, 进行测量。
(2)每次将鸡蛋大头朝上竖直置于高光谱仪上面的透射光源箱孔口, 保证透射光源箱没有漏光, 丝杆式移动平台至合适位置, 通过相机采集鸡蛋的透射高光谱数据。
(3)采集光谱数据后, 用电子天平测鸡蛋样品的蛋重, 再用游标卡尺测量蛋白高度。
(4)记录所有数据, 根据鸡蛋蛋重和蛋白高度来计算鸡蛋哈夫单位值。
图1为3种不同新鲜等级鸡蛋的原始光谱曲线图。
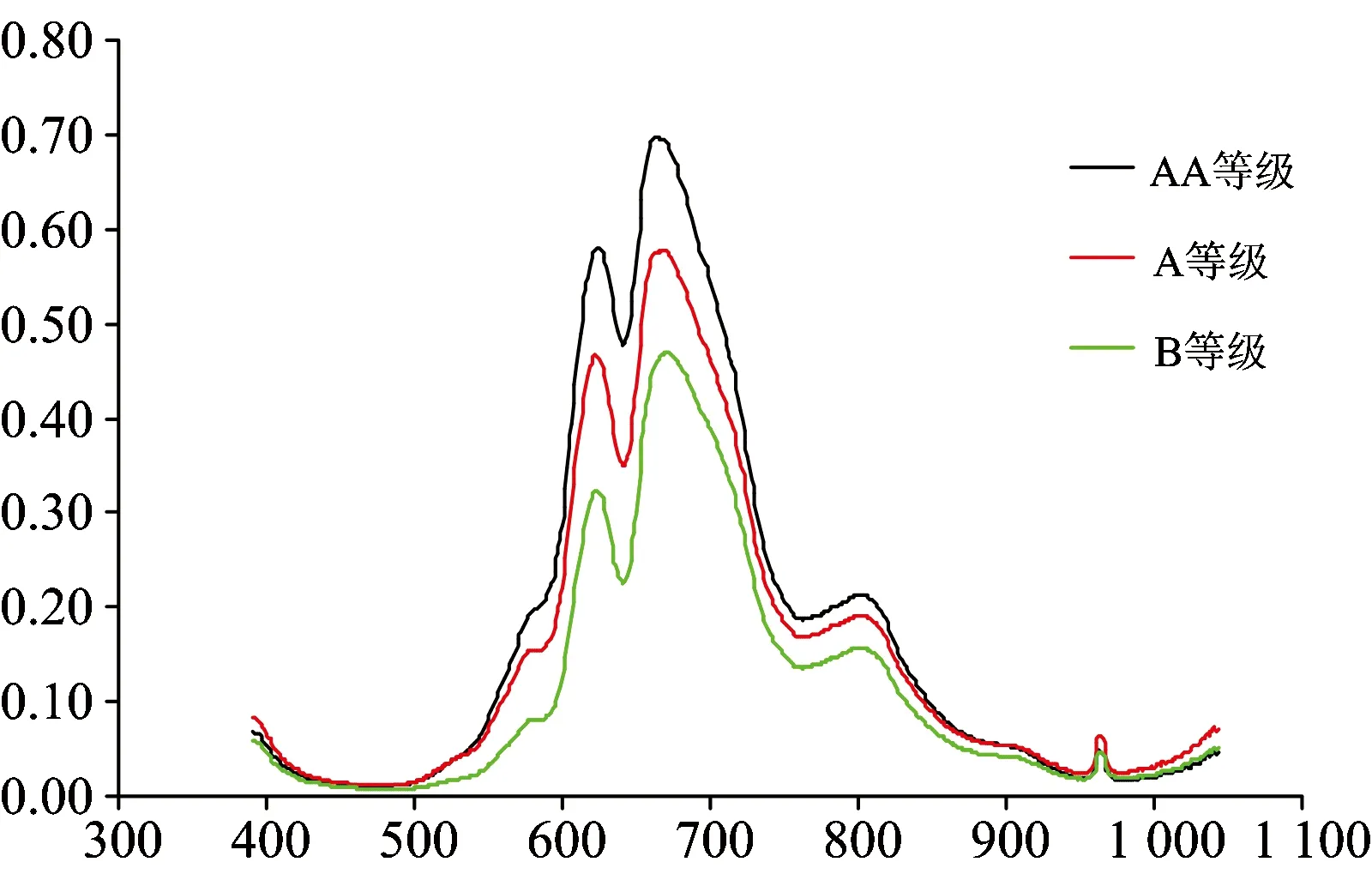
图1 不同等级鸡蛋原始高光谱曲线
2 结果与讨论
2.1 光谱数据预处理
从图1看出原始光谱曲线的高光谱数据, 比较杂乱, 且含的信息量不足, 不能直接发现规律, 光谱曲线也有明显的噪声信号存在, 这些噪声信号将会对后续的提取特征参数和建立模型等过程造成干扰, 直接影响模型预测的准确性, 因此在提取特征参数之前需要对原始高光谱数据进行预处理。 本文中, 高光谱数据的预处理在MATLAB中完成, 对光谱的预处理包括马氏距离剔除异常样本, 微分校正, 小波去噪, 光滑处理及标准化处理等。
2.1.1 马氏距离剔除异常样本
由于高光谱成像仪精度限制和噪声等因素的存在, 获取的鸡蛋高光谱数据中不可避免的存在一小部分的异常数据[9]。 如果不消除异常值, 会影响数据处理效果, 故消除异常值对后面处理结果的质量和精度非常重要。 本文对样品鸡蛋高光谱数据异常样本数据剔除采用了马氏距离判别法。

图2 马氏距离
鸡蛋样本集中各样本和平均样本的马氏距离散点图如图2所示。 由图可知, 由于165个样本的马氏距离基本都在0.8以内, 故本研究中将鸡蛋高光谱数据的马氏距离阀值设为0.8, 则马氏距离大于0.8的鸡蛋样本即被判为异常样本, 从图2可以看出有8个鸡蛋样本异常(其编号分别为: 14, 42, 54, 67, 80, 119, 134和162)。
2.1.2 微分处理
微分处理可以消除光谱基线中的平移和散射, 并有效的消除背景干扰, 还可以通过对重叠的波峰进行分辨, 提高其分辨率及灵敏度[10]。
在对样品鸡蛋高光谱数据进行其他预处理之前, 首先用不同微分的鸡蛋高光谱数据对其新鲜度进行分析, 选择最适合本研究的微分阶数。 本研究分别用不进行微分处理的高光谱数据、 一阶微分数据和二阶微分数据, 采用偏最小二乘法分别建立不同微分的鸡蛋新鲜度的分析模型(如图3所示)。
图3中, (a)为未对鸡蛋高光谱数据进行微分的新鲜度分析模型, (b)为高光谱数据一阶微分的新鲜度分析模型, (c)为高光谱数据二阶微分的新鲜度分析模型。 对比发现鸡蛋高光谱二阶微分的新鲜度分析模型的相关系数比其他两个模型都大, 其误差均方根比另两者小, 说明二阶微分效果最好, 故本研究将对鸡蛋高光谱二阶微分数据做进一步处理(以下出现的高光谱数据均指高光谱二阶微分数据)。
2.1.3 小波去噪与光滑处理
对二阶微分后的高光谱数据进行小波去噪, 再进行光滑处理, 光滑处理分为: 移动平均法、 Savitzky-Golay法和厢车平均法等。
由于光滑处理中窗口宽度与光谱分辨率成反比, 窗口宽度选择不当, 不仅使光滑滤波效果不明显, 还有可能引起光谱数据失真。 经过反复试验, 采用窗口宽度为9的移动平均法对小波去噪后的高光谱二阶微分数据进行光滑处理, 光滑效果见图4。 最后对光滑后的光谱数据进行了标准化处理。
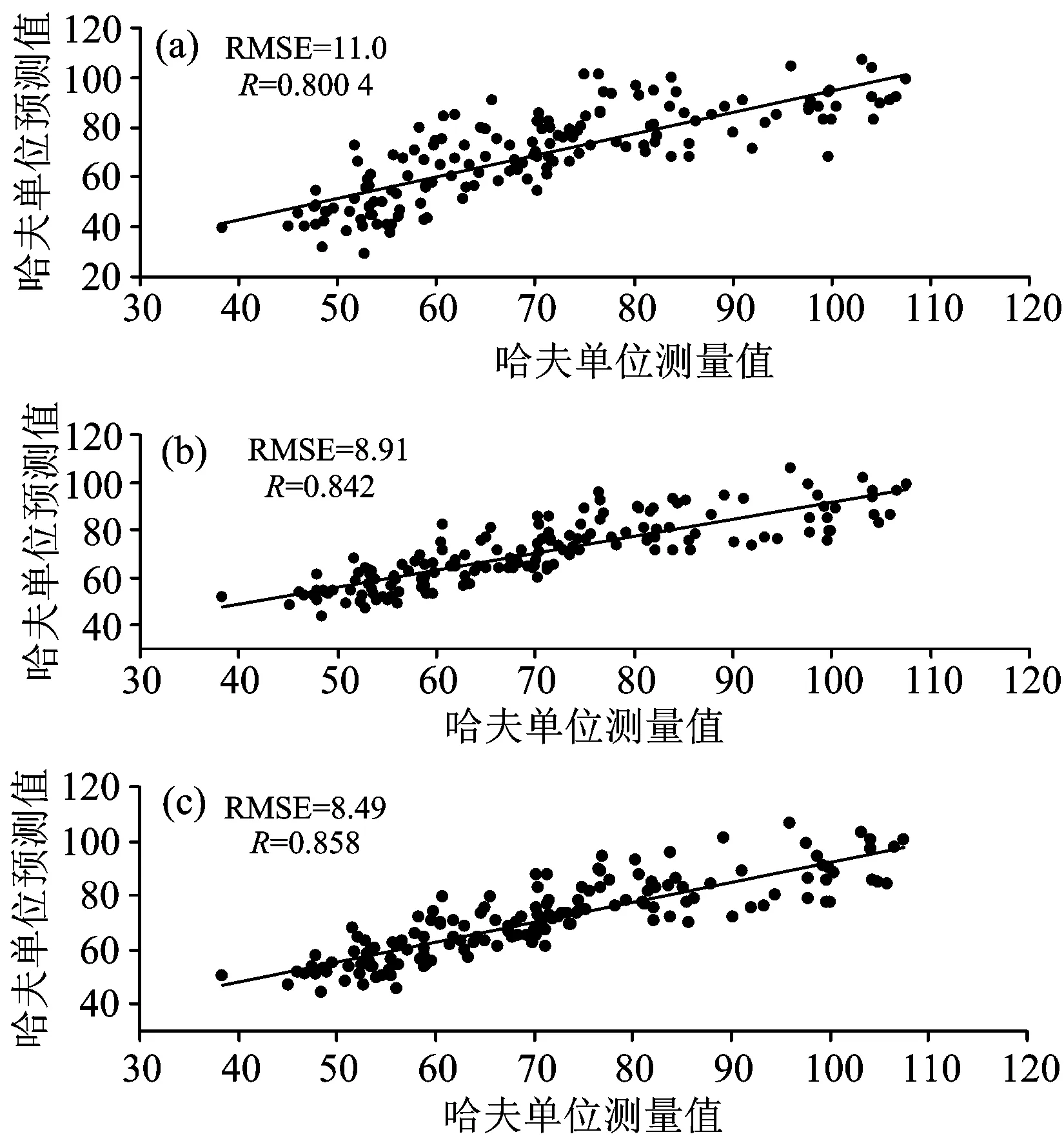
图3 基于高光谱不同微分的鸡蛋新鲜度分析模型
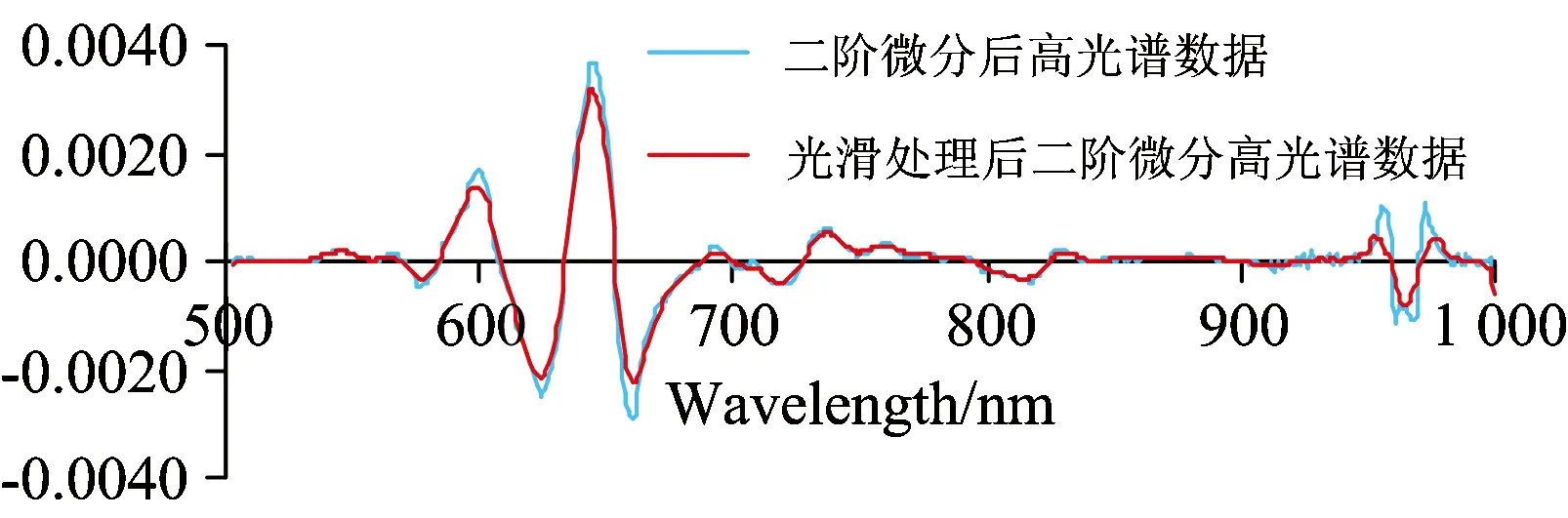
图4 光滑处理前后的高光谱曲线
2.2 CARS变量选取法提取特征参数
2.2.1 竞争性自适应重加权算法
竞争性自适应重加权算法(即CARS变量选取法)是近年刚提出来的一种变量选取方法, 是在达尔文进化理论“适者生存”原理的基础上建立起来的, 选择偏最小二乘回归模型中回归系数较大波段的变量值(即光谱值), 淘汰掉相关系数较小波段的变量值, 以此选择出一组特征波段, 用其组合来代表整个波段内的光谱信息, 达到数据降维的目的[11]。 CARS变量选取法的主要步骤为:
(1)采用蒙特卡罗采样法(Monte Carlo sampling, MCS)对样本进行抽样, 一般选用样品总数的80%作为校正集, 然后建立样本的PLS模型。
(2)假设试验测得样本的高光谱矩阵为Xm×n, 其中m为样本数,n为变量数(此处为波段数);ym×1为实际测量的新鲜度(Hu)矩阵, 则建立的PLS模型如式(2)所示
y=Xb+e
(2)
式(2)中,b为高光谱矩阵X中变量对应的n维系数向量, 且有b=Pc=Lc=[b1,b2,b3, …,bn]T(L表示X矩阵中各波段在PLS模型中的得分矩阵),e表示模型预测集的残差,bi表示第i个高光谱波段的光谱值对模型的贡献, 其绝对值越大, 表示对模型的作用越大。
(3)研究中CARS变量选取的采样次数P次, 用|bi|值较小的个光谱波段去除以指数衰减函数, 那么i次采样后的指数衰减函数为式(3)
(3)
其中,a和k均为常数, 可以通过第一次和第P次参与建模的变量个数计算, 第一次参与建模的变量为n个, 第P次参与建模的变量为2个, 故a,k的计算公式分别为式(4)和式(5)
(4)
(5)
(4)对变量再进行自适应重加权(adaptive reweighted sampling, ARS)采样, 主要利用进化论“适者生存”的原则, 也是CARS变量选取法的核心, 通过计算各光谱在每个波段处的权重进一步对变量进行筛选, 权重计算公式为式(6)
(6)
(5)对比每次新筛选变量产生新的子集的交叉验证均方差(root-mean-squares error of cross-validation, RMSECV), 其中RMSECV值最小的变量组成的子集就是最佳的变量子集。
2.2.2 CARS变量选取法提取特征参数
图5为CARS变量选取法选取样品鸡蛋高光谱二阶微分数据特征变量选取的过程, 其中图5(a)为筛选过程中变量的变化过程, 图5(b)表示交叉验证均方差的变化过程, 图5(c)为CARS变量选取过程。 选出32个样品鸡蛋高光谱二阶微分数据的特征波长, 具体的波段详见表1所示。
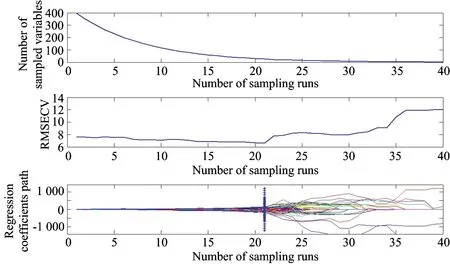
图5 CARS法选取波长变量过程
2.3 鸡蛋新鲜度预测模型
对165个白壳蛋样本的校正集和验证集划分, 按照常用的2∶1随机分配原则, 分别建立样品鸡蛋高光谱全波段二阶微分的PLS新鲜度预测模型和基于CARS变量选取法得到的特征参数的PLS新鲜度预测模型。
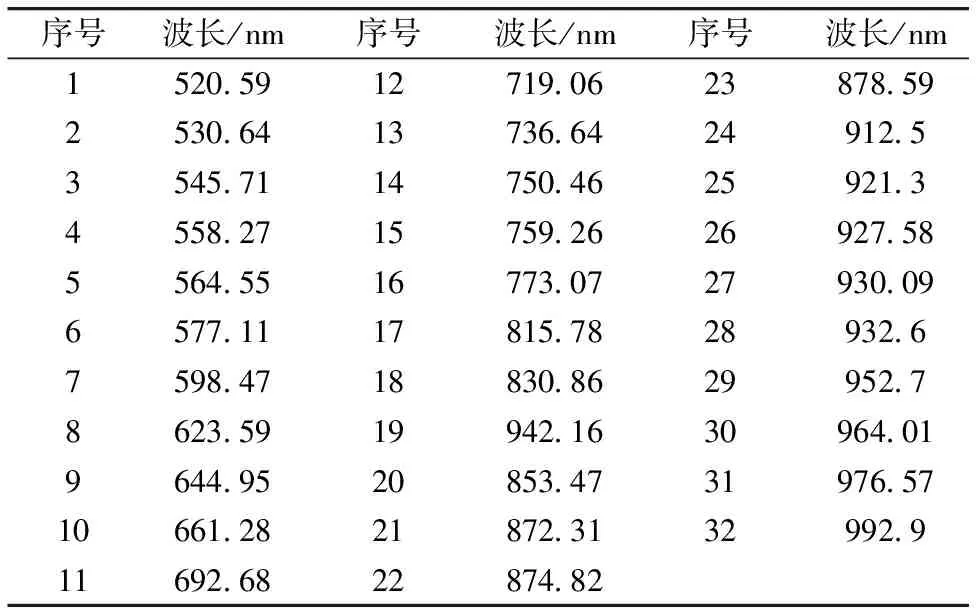
表1 CARS法选取的特征波长
图6(a)为全波段预测集的PLS模型验证图, 图6(b)为特征参数多元回归模型的PLS预测效果图。 全波段的PLS预测模型验证集的相关系数为0.88, 其均方误差为7.565; 特征参数模型的多元回归模型验证集的相关系数为0.93, 均方误差为6.44。
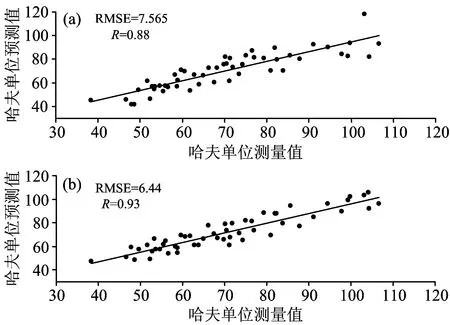
图6 模型的验证图
国内的行业标准(SBT 10638—2011)对鸡蛋新鲜度界定如表2所示。

表2 鲜鸡蛋品质分级要求
表3与表4分别是模型的验证结果及新鲜度判别结果。
从表3可以看出两种模型对白壳蛋AA等级蛋新鲜度的

表3 模型的验证结果

表4 模型的新鲜度判别结果
判别准确率最高达90%, A等级的判别准确率最高达79%, 对B等级判别的准确率最高达88%; 从对每个新鲜度等级判别的准确率来看, 特征参数的多元回归法对AA等级和A等级白壳蛋的判别准确率最高, 高光谱二阶微分全波段的PLS模型对B等级白壳蛋的判别准确率最高。
由表4可以看出来, 两个模型中对新鲜白壳蛋的判别准确率最高可达到100%, 对不新鲜白壳蛋的判别准确率最高可达88%。
3 结 论
以白壳蛋为研究对象, 利用高光谱成像技术采集样品蛋的高光谱数据, 通过分析高光谱数据研究其内部品质(新鲜度), 建立了鸡蛋新鲜度两种预测模型。
(1)用马氏距离剔除异常鸡蛋样本, 发现高光谱二阶微分数据的预测效果最好。
(2)基于高光谱二阶微分全波段PLS模型验证集的相关系数为0.88, 均方误差分别为7.565; 基于特征参数多元回归模型验证集的相关系数为0.93, 均方误差为6.44。
(3)比较两种预测模型的鸡蛋不同新鲜度等级的判别率, 其中AA等级和B等级的判别比较准确, A等级判别准确率较低。 对AA等级判断的最高准确为90%, 对A等级判别的准确率为79%, 对B等级判别的准确率为88%。
(4)从判别鸡蛋是否新鲜方面来看, 两个模型的判别效果都比较好, 判别白壳蛋新鲜和不新鲜的最高准确率分别达100%, 88%。
[1] WANG Qiao-hua, WEN You-xian, LIN Xue-dong, et al(王巧华, 文友先, 林雪冬, 等). Transactions of the Chinese Society of Agricultural Engineering(农业工程学报), 2008, 3: 179.
[2] Sun L, Yuan L M, Cai J R, et al. Food Analytical Methods, 2015, 8(4): 922.
[3] Nicolas A N, Michael N, Shiv P, et al. Food and Bioprocess Technology, 2011, 4(5): 731.
[4] ZHANG Wei, PAN Lei-qing, TU Kang(张 伟, 潘磊庆, 屠 康). Transactions of the Chinese Society of Agricultural Engineering(农业工程学报), 2012, 28(21): 149.
[5] Smith D P, Lawrence K C, Heitschmidt G W. International Journal of Poultry Science, 2008, 7(10): 1001.
[6] Mahmoud Sotani, Mahmoud Omid, Reza Alimardani. Food Analytical Methods, 2015, 8(3): 710.
[7] Wei Z, Leiqing P, Kang T, et al. Plos One, 2014, 9(2): 1.
[8] ZHOU Zhu, LI Xiao-yu, GAO Hai-long, et al(周 竹, 李小昱, 高海龙, 等). Transactions of the Chinese Society of Agricultural Machinery(农业机械学报), 2012, 2: 128.
[9] MA Shuai-qi, BAO Cun-hui(马帅旗, 鲍存会). Electronics Optics & Control(电光与控制), 2014, 6: 72.
[10] CHU Xiao-li, YUAN Hong-fu, LU Wan-zhen(褚小立, 袁洪福, 陆婉珍). Progress in Chemistry(化学进展), 2004, 4: 528.
[11] LI Jiang-bo, PENG Yan-kun, CHEN Li-ping, et al(李江波, 彭彦昆, 陈立平, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2014, 34(5): 1264.
Egg Freshness Detection Based on Hyper-Spectra
WANG Qiao-hua1, 2, ZHOU Kai1, WU Lan-lan1, WANG Cai-yun1
1. College of Engineering, Huazhong Agricultural University, Wuhan 430070, China
2. National Research and Development Center for Egg Processing, Huazhong Agricultural University, Wuhan 430070, China
This research collected the transmission hyper-spectral data of eggs with hyper-spectral imager. Haugh unit value was used as freshness norm. With the help of MATLAB and SAS software combined with stechiometry method, the hyper-spectral data of sample eggs was analyzed and processed. The prediction model of egg freshness was established based on hyper-spectral technology. The research chose the band range from 500 to 1 000 nm as sensitive band. The hyper-spectral data of abnormal samples were removed by using mahalanobis distance. Differential correction was done on hyper-spectral data. After the comparison, there was a high linearity between the second-order differential data of hyper-spectra and haugh unit value. Therefore, this paper conducted a further research on the second-order differential data of hyper-spectra. And it was treated with wavelet denoising, smoothing and standardizing. This paper chose the newly proposed CARS variable selection method to do dimensionality reduction on hyper-spectral data. And thirty-two characteristic parameters were extracted. They were used to establish partial least square prediction model based on all band and multiple regression model based on characteristic parameters on white shell eggs. The correlation coefficients of white shell eggs were 0.88 and 0.93 respectively, and the corresponding mean square errors being 7.565 and 6.44. Inspections were conducted on PLS prediction model based on all band hyper-spectral second-order differential and multiple regression model based on characteristic parameters by using eggs of validation set. The accuracy rates of these two models to discriminate white shell eggs’ freshness and non-freshness were 100% and 88% respectively.
Egg; Freshness; Hyper-spectra; Partial least square; CARS
Jun. 1, 2015; accepted Oct. 24, 2015)
2015-06-01,
2015-10-24
国家自然科学基金项目(31371771), 公益性行业(农业)科研专项(201303084), 国家科技支撑计划项目(2015BAD19B05)资助
王巧华, 女, 1970年生, 华中农业大学工学院教授 e-mail: wqh@mail.hzau.edu.cn
O657.3
A
10.3964/j.issn.1000-0593(2016)08-2596-05

