平顶药型罩聚能射流形成过程研究

王德宝， 马宏昊， 沈兆武， 陈 伟， 曲忠伟

(1.中国科学技术大学 近代力学系, 合肥 230027; 2.安徽理工大学 理学院, 安徽淮南 232001)



平顶药型罩聚能射流形成过程研究

王德宝1， 马宏昊1， 沈兆武1， 陈 伟1， 曲忠伟2

(1.中国科学技术大学 近代力学系, 合肥 230027; 2.安徽理工大学 理学院, 安徽淮南 232001)

摘要：ANSYS/LS-DYNA对平顶药型罩的射流形成过程进行数值模拟，结果表明，在顶点起爆条件下，平顶药型罩的平顶中心首先下凹并拉动药型罩边壁向内汇聚，使得存在夹角的平顶与边壁整体构成环形线性聚能罩，此聚能罩在炸药爆轰作用下产生一级射流，一级射流彼此作用继而产生更高速度的二级射流。分析认为其机理是二级药型罩成型假说，尝试探索研究多级射流领域，并为提高射流速度提供一种新思路。

关键词：聚能射流； 平顶药型罩； 数值模拟； 理论分析； 二级射流

1引 言

2平顶药型罩装药结构物理模型

装药结构物理模型如图1所示，由平顶药型罩、炸药、装药壳体、起爆装置构成。其中，壳体材料为45#钢，厚1.2mm；炸药采用细RDX；药型罩为紫铜平顶药型罩，底面直径20mm，锥角为60°，平顶外直径6mm、内直径4mm。

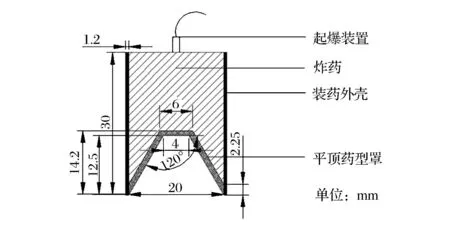
图1　平顶药型罩聚能装药结构剖视图Fig.1　Section view of the shaped charge with a flat-top liner

3数值模拟模型

3.1基本假设

整个爆炸过程为绝热过程；炸药、药型罩均为连续均匀介质；装药结构具有严格轴对称特点。整个变化过程可以通过定常理想不可压缩流体力学理论阐释。

3.2算法选择

采用ANSYS/LS-DYNA软件提供的Lagrange、Euler、ALE三种算法。其中Lagrange方法多用在固体结构的应变应力分析，然而用其处理大变形问题时，容易出现网格严重畸变，阻碍计算进行。

而Euler方法对于物质边界的捕捉较为困难，常用于流体分析。

ALE方法兼顾Lagrange方法和Euler方法的优点，即是本研究采用的方法。其在边界物质的网格划分上吸收了Lagrange方法的优点，使其能够有效跟踪物质结构的运动；其次在内部处理上引进Euler网格特点，网格可以根据需要适当调整，使得网格不至于出现严重畸变，正适用于研究大变形射流问题。

3.3材料选择

3.3.1炸药参数

主装药的物态方程采用标准的JWL物态方程，可以表示为：

(1)

式中：ω，Α，B，R1，R2为实验拟合常数；E为初始内能，RDX炸药具体参数如表1所示。

表1　RDX炸药计算参数

3.3.2药型罩参数

药型罩材料为紫铜，在程序中采用状态方程表达应力张量的球张量、能量和密度之间的关系，并用本构模型描述偏应力和偏应变之间的关系。计算采用EOS_GRUNEISEN状态方程及Steinberg本构模型。

GRUNEISEN状态方程可以表示为：

(2)

其具体参数如表2所示。

表2　紫铜药型罩计算参数

3.3.3空气参数

空气材料使用空气材料模型，在关键字文件中进行参数修改，采用流体材料的状态方程EOS_LINEAR_POLYNOMIAL，具体材料参数见表3。

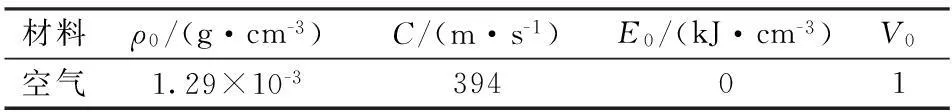
表3　空气计算模型

3.4模型建立

依据图1所示模型，等比例建模。包含炸药、平顶药型罩、空气三种材料模型，采用LS-DYNA有限元程序中多物质ALE算法模拟平顶药型罩中心点起爆状态下药型罩变化过程〔5〕。由于模型具有轴对称性，建立1/4的三维模型，如图2所示。通过施加边界条件保证计算精度。空气、炸药、药型罩采用Euler网格。

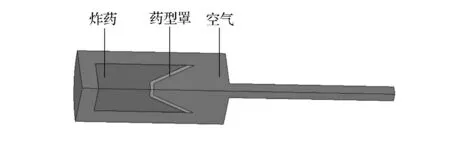
图2　平顶药型罩聚能装药结构的1/4计算模型Fig.2　1/4 calculation model of the shaped charge with a flat-top liner

4数值模拟结果及分析

4.1平顶药型罩射流形成过程

平顶药型罩射流形成过程中的5个阶段如图3所示。

图3　射流形成过程中5个阶段Fig.3　Five stages of jet formation

从图3中可以看出，顶点起爆方式下，药型罩平顶中心微元首先被压垮下凹，平顶与侧壁之间开始形成一级射流，4.0μs时一级射流形态稳定。由于实体药型罩为圆锥结构，因此平顶与侧壁之间实际上形成一圈环形一级射流，在标准的平顶药型罩结构中，这一圈一级射流汇聚在中心轴线上产成二次变化，形成4.5μs时刻的二级射流。

因为平顶锥形罩具有对称特性，因此简化为二维结构进行分析。选取4.0μs时刻下一级射流头部元素H129176和4.5μs时刻二级射流初步形成期元素H114796，其纵向速度如图4所示。

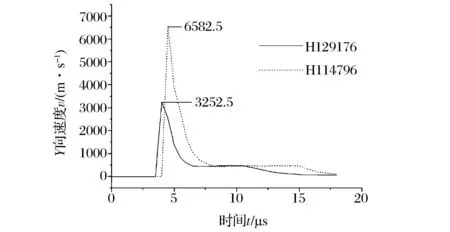
图4　元素H129176和H114796纵向速度示意图Fig.4　The longitudinal velocity of elements H129176 and H114796

从图4中可见，一级射流头部速度只有3 252.5m/s左右，经过二次碰撞，形成的二级射流速度瞬间增加到6 582.5m/s。

4.2一级射流形成过程分析

平顶药型罩的平顶与侧壁之间具有一定夹角α，构成一种线性环形聚能罩。在传统线性聚能装药结构中，当线性聚能罩顶角大于100°时容易形成自铸破片〔6-8〕。本文所研究模型中α=120°，然而其变形过程却不同于传统线性药型罩。

不同形状药型罩装药结构中爆轰波传播路径如图5所示。

图5　不同形状药型罩装药结构中爆轰波传播示意图Fig.5　The detonation wave propagation in charges with different liner

传统大锥角药型罩装药结构剖面图如图5(a)所示，正向中心顶点起爆方式下，爆轰波首先到达罩顶点微元d，在高压高速的爆轰作用下，迅速下移，造成翻转，后续爆轰产物继续作用，形成的翻转弹丸整体下移发挥聚能射流作用；然而平顶药型罩变化过程却与此不同。

如图5(b)所示，药型罩平顶微元D首先受爆轰压力作用，内凹下移到位置D′，使得平顶与侧壁之间夹角α减小，形成一圈小锥角环形线性聚能罩。此线性聚能罩顶角α的中心线与竖向垂线之间存在夹角β。理论推知，当锥形/线性药型罩接受顶点正向起爆时，夹角β值等于零。此模型中平顶药型罩在爆轰作用下，其平顶中心的下移会拉动整个环形线性聚能罩向中心靠拢，导致β角减小；并且，相比于BC面，AB面受爆轰压力作用有一定延迟。两种影响因素相互耦合，使得环形聚能罩接受近似顶点起爆的效果，形成稳定的一级射流。

4.3二级射流形成过程分析

对于二级射流的形成过程，本文提出两种假说：成熟一级射流对撞成型假说，认为平顶与边壁产生完善的一级射流，在中心轴线汇聚碰撞，产生更高速度的二级射流。一级射流形成呈高速运动状态的二级射流药型罩，继而产生二级射流。以下对两种假说进行分析验证。

4.3.1成熟一级射流对撞成型假说

(1)假说详细内容

通过爆轰波顶端压合、侧向延时作用，平顶药型罩结构中平顶与侧壁之间首先形成环形线性聚能罩，继而被压垮产生一级射流。假设炸药严格从中心顶点起爆；爆轰波在炸药中各向传播速度、波峰压力均匀稳定，并且一级射流成长完善。在此理想条件下结合经验公式，应用定常不可压缩射流形成理论，B、C处形成的一级射流速度大小、方向相同，都向中心点F汇聚,如图6所示。

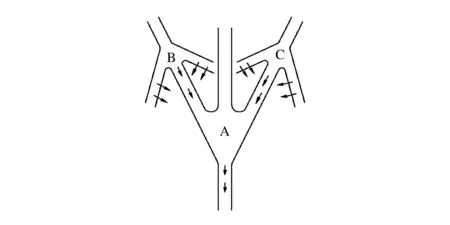
图6　两次射流形成过程示意图(静坐标)Fig.6　Formation process of jet(Static coordinate system)

一个环形聚能罩形成的环形射流刀汇聚在F点进行二次碰撞，与射流的一次碰撞原理相同，碰撞过后射流的一部分向上运动形成二级杵体，另一部分向下运动形成二级射流。

(2)平顶药型罩射流头部速度分析

依据经典定常理想不可压缩流体力学理论，以碰撞点B为参考坐标系，B点附近药型罩的运动如图7所示。

图7　一级射流形成过程(动坐标)Fig.7　Formation process of primary jet (Moving coordinate system)

其中v1为碰撞点B沿射流形成方向整体移动速度，v2为罩壁向碰撞点的相对流动速度，v3为一级射流离开碰撞点的相对速度。根据伯努利方程描述，即流体各处的压力和单位体积动能的综合为常数，对于图7中聚能罩壁P点和一级射流上Q点，可得下式：

(3)

式中：pp和pq为流体中P点和Q点的静压力；d为流体密度。假设P点和Q点距离碰撞点B很远，则其静压力pp、pq和周围气体压力相等，因此可得：

ν2=ν3

(4)

则一级射流的绝对速度：

ν3′=ν1+ν3

(5)

同样，对于C碰撞点以及整个环形线性聚能罩所得的一级射流速度均为v3′。

由于平顶锥形结构的对称性，使得一级射流最终汇聚于一点，即图8所示F点。

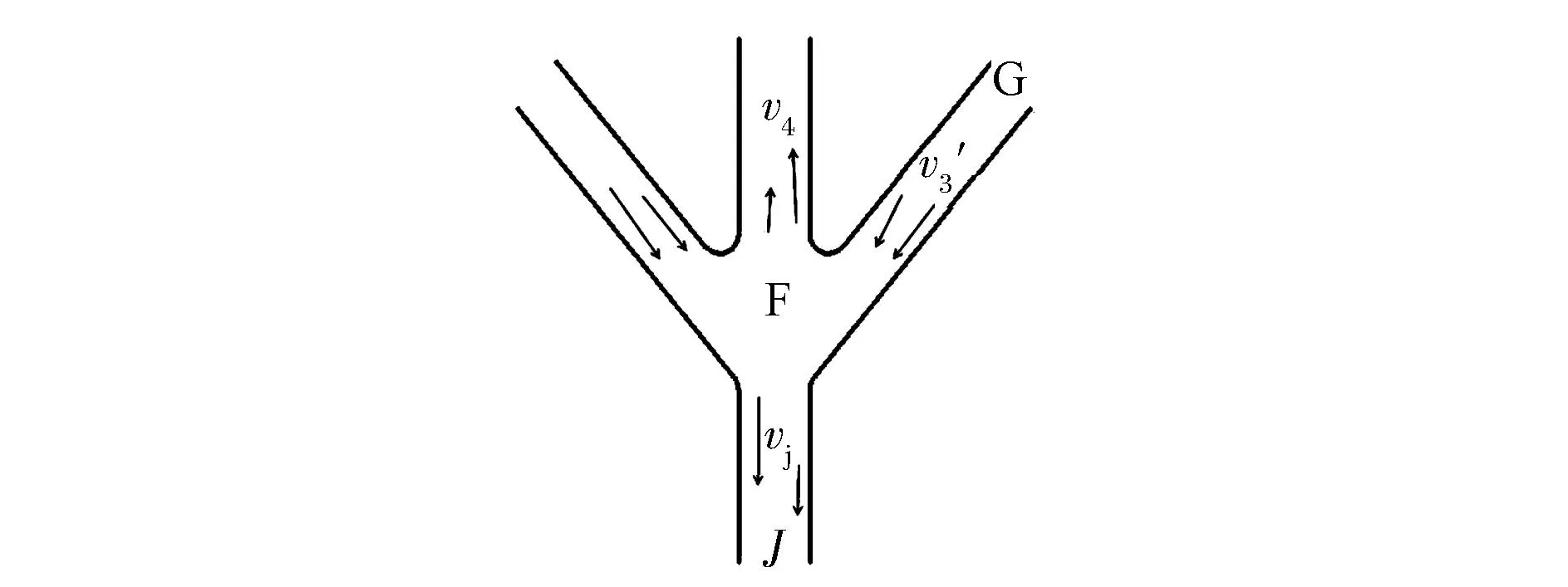
图8　二级射流形成过程Fig.8　Formation process of the second level jet (Static coordinate system)

对F点进行分析，则二次碰撞过程中，碰撞点F为静止状态，一级射流以v3′的速度汇聚于碰撞点F，形成以v4为相对速度的杵体和vj为相对速度的二级射流。

对一级射流点G和二级射流点J应用伯努利方程可得：

(6)

同上所述，

νj=ν3′

(7)

二级射流的绝对速度：

ν=ν3′=ν1+ν3

(8)

式(8)就是成熟一级射流对撞假说下平顶药型罩产生的二级射流速度公式。在传统一次射流的基础上汇聚碰撞产生二级射流。与文献〔6〕所提及的同属性药型罩效果相同，并不能提高速度。

4.3.2二级药型罩成型假说

(1)假说内容

环形线性药型罩首先形成一级射流，但是一级射流形成之后并没有得到良好发育，在极小的空间内彼此挤压堆积，形成一个本身具备一级射流速度的二级锥形药型罩，锥角为∠MON。如图3(c)所示，对此时的平顶药型罩做一个中轴剖面如图9所示。二级药型罩存续时间极短，在其存续期间，二级药型罩受到爆轰压力作用产生二级射流。

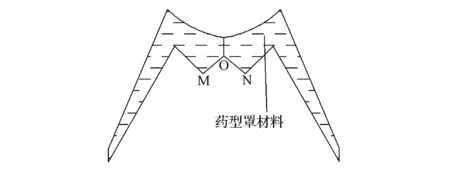
图9　二级药型罩结构剖面图Fig.9　Section view of the second level liner

(2)平顶药型罩射流头部速度分析

一级射流的形成与之前分析相同，即依据伯努利方程，可得一级射流速度ν3′=ν1+ν3，并且二级药型罩的速度与一级射流速度相同。

以一级射流的速度建立动坐标系，二级药型罩再次压合形成射流，射流在足够的空间下得以正常成型。则二级射流的速度：

ν=ν1+ν3+ν3′

(9)

即ν=2ν3′，与模拟结果相吻合。

两种假说的分析结果表明，二级药型罩成型假说更为合理。与一级射流对撞成型假说相比，二级药型罩成型假说的成立基础是药型罩顶部空间狭小，一级射流得不到有效成长。

5结 论

(1)平顶药型罩形成聚能射流的过程分为两个阶段：首先是平顶与边壁作为环形线性聚能药型罩形成一圈环形线性一级射流；对称分布的一级射流在狭小空间内挤压碰撞形成二级药型罩，继而形成二级射流。

(2)二级射流头部速度是一级射流的两倍。

(3)通过特定小尺寸的平顶药型罩可以形成高速二级射流，这为提高射流速度提供了一种新思路，同样原理下，可以探索三级射流甚至更高层级射流的形成。

参考文献(References)：

〔1〕 李磊. 多面聚能效应的数值模拟与应用研究[D]. 合肥: 中国科学技术大学,2013.

LI Lei. Numerical simulation and application of multidimensional shaped charge effect[D]. Hefei: University of Science and Technology of China,2013.

〔2〕 马建福. 聚能装药结构对混凝土侵彻作用研究[D]. 太原: 中北大学,2007.

MA Jian-fu. Study on the mechanism of penetrating into concrete using shaped charge structures[D]. Taiyuan: North University of China, 2007.

〔3〕 张雷雷,朱鸿瑞,黄风雷. 大锥角药型罩聚能装药结构对混凝土介质侵彻研究[J]. 弹箭与制导学报,2007,27(3):134-136.

ZHANG Lei-lei, ZHU Hong-rui, HUANG Feng-lei. Shaped charge with large cone angle penetration to concrete target[J]. Journal of Projectiles, Rockets, Missiles and Guidance,2007,27(3):134-136.

〔4〕 刘波, 姚志敏. 聚能破甲战斗部药型罩不同形状锥顶对射流影响的数值模拟[J]. 机械设计与研究,2014,30(4):78-81.

LIU Bo, YAO Zhi-min. The numerical simulation for conical liners with different shape tops of shaped charge warhead impacting on the jets[J]. Machine Design and Research, 2014,30(4):78-81.

〔5〕 王成,付晓磊,宁建国. 起爆方式对聚能射流性能影响的数值分析[J]. 北京理工大学学报,2006,26(5):401-404.

WANG Cheng, FU Xiao-lei, NING Jian-guo. Numerical simulation of shaped charge jet formation under different ways of initiation[J]. Transactions of Beijing Institute of Technology, 2006,26(5):401-404.

〔6〕 焦丽娟,刘天生. 关于楔形罩的初步研究[J]. 华北工学院学报,2001,22(1):70-74.

JIAO Li-juan, LIU Tian-sheng. Preliminary study on the cuneiform charge liner[J]. Journal of North China Institute of Technology, 2001,22(1):70-74.

〔7〕 董永香,陈国光,辛长范,等. 一种新型装药结构的探讨[J]. 华北工学院学报,1999,20(3):233-235.

DONG Yong-xiang, CHEN Guo-guang, XIN Chang-fan, et al. Analysis on the structure of a new type of shaped charge[J]. North China Institute of Technology, 1999, 20(3):233-235.

〔8〕 徐景林，顾文彬，武双章，等. 带隔板线型聚能装药侵彻能力的正交优化[J]. 工程爆破，2016,22(1)：77-81.

XU Jing-lin, GU Wen-bin, WU Shuang-zhang, et al. Orthogonal optimization of penetration ability of linear shaped charge with wave-shaper[J]. Engineering Blasting, 2016,22(1): 77-81.

Study of shaped charge jet formation process with flat-top liner

WANG De-bao1, MA Hong-hao1, SHEN Zhao-wu1, CHEN Wei1, QU Zhong-wei2

(1. Department of Modern Mechanics, University of Science and Technology of China, Hefei 230027, China;2. Faculty of Science, Anhui University of Science and Technology, Huainan 232001, Anhui, China)

ABSTRACT：Jet formation of flat-top liner was numerically simulated by the software ANSYS/LS-DYNA. The results showed that the ceiling of flat-top liner was concaved by explosive effect, then the whole liner wall was pushed inside to form an annulus linear shaped charge cover because of the angle between liner ceiling and liner wall. The primary jet was produced by the annulus liner under the action of explosive detonation. Primary jet collided with each other in the central axis to form the second level jet with higher velocity. The formation process of second-level jet could be explained by the second level liner hypothesis. The new idea about how to improve the jet velocity was given to try to explore the multi-level jet field.

KEY WORDS:Shaped charge jet； Flat-top liner； Numerical simulation； Theory analysis； Second level jet

文章编号：1006-7051(2016)02-0051-05

收稿日期：2015-10-20

基金项目：储氢型动态敏化复合乳化炸药爆轰机理和安全性研究(项目批准号：51374189)

作者简介：王德宝(1989-)，男，硕士，主要从事低振动隧道掏槽爆破研究。E-mail：wangdb@mail.ustc.edu.cn

中图分类号：TD235.2； TJ410

文献标识码：A

doi：10.3969/j.issn.1006-7051.2016.02.011