多室薄壁箱梁腹板弯曲剪力流计算及截面参数分析

王　强，姜天华，邹　垚，孙　杰

(武汉科技大学城市建设学院，湖北 武汉，430065)



多室薄壁箱梁腹板弯曲剪力流计算及截面参数分析

王强，姜天华，邹垚，孙杰

(武汉科技大学城市建设学院，湖北 武汉，430065)

摘要：基于薄壁杆件结构理论，推导出多室薄壁箱梁腹板弯曲剪力流的计算公式，将其应用于钢箱梁剪力流的计算，并与有限元分析结果及已有文献中的计算结果相比较，同时分析了有无悬臂板、悬臂板厚度、梁高、腹板厚度、底板厚度和箱室宽度对腹板剪力流分配的影响。结果表明，所推导的公式具有较高的精度；腹板厚度、悬臂板厚度及箱室宽度为多室薄壁箱梁腹板剪力流分配比的主要敏感参数，梁高与底板厚度为次要敏感参数；在桥梁结构受力分析中，为简化计算而不考虑悬臂板，会降低边腹板的荷载分配比，导致横隔梁的设计安全系数下降。

关键词：薄壁杆件；多室薄壁箱梁；剪力流；有限元；截面参数

大跨度桥梁的建设中，多室薄壁箱梁的应用十分广泛。由于多室薄壁箱梁受力弯曲时各个腹板的剪力流分布存在差异，且分配比例尚不明确，因此有必要对剪力流的分配及其影响参数进行分析，以此来正确掌握薄壁箱梁的受力状况并对多室箱梁截面进行优化设计。现有关于剪力流的研究[1-5]多借助有限元软件对剪力的分配比进行分析，而关于影响剪力流分配的参数研究较少。苏继宏等[6]采用壳体单元建模验证了有限元模拟腹板剪力传力比的正确性，仅对有无翼缘板两种情况进行了分析比较。张映高[7]采用梁格法建模分析了不同结构形式的腹板剪力流分配比，但并未对具体参数进行分析。张旭慧[8]采用悬臂两点加载法建模来分析薄壁腹板剪力流，也仅验证了有限元法的适用性。为此，本文基于薄壁杆件结构力学理论[9-11]，推导了多室箱梁腹板弯曲剪力流计算公式，选取非对称截面进行计算分析，并结合现有文献计算结果及有限元法验证了公式的正确性。同时按一定比例调整箱室截面参数，分析多室箱梁腹板剪力流分配比的变化，以期得出影响多室箱梁剪力流分配的主要参数与次要参数。

1多室箱梁剪力流的理论分析

1.1薄壁杆件弯曲剪应力分析

如图 1所示，具有n室闭口截面的薄壁杆件，其中有n次超静定次数，须考虑n个位移协调平衡条件。将原结构(图1(a))转化为多个开口截面(图1(b)～(e))进行分析。此开口截面杆件在剪力作用下的剪力流为q0，且每一箱室切口处存在未知剪力流qr(r=1,2，…，n)。每一切口在q0和qr作用下，切口两边的纵向相对位移为零，因此第i室内切口处的位移协调条件可表达为

(1)

式中:∮i为沿着第i室周边的闭路积分；γ为各箱室的剪切变形；s为截面轮廓线曲线坐标，以逆时针方向为正;q为多室箱梁断面总的剪力流;G为箱室材料的剪切模量；δ为箱室壁厚。

式(1)中，

(2)

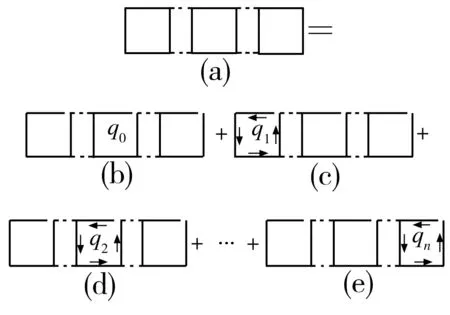
图1　多室闭口截面剪力流示意图

Fig.1 Schematic diagram of shear flow for multichambered closed section

将式(2)代入式(1)并积分，同时考虑qr的分布特点，得到第i室的位移协调条件为

(3)

式中: qi为第i室的剪力流;qk为与i室隔壁的第k室的剪力流；∮ik表示沿相邻的i室和k室的公共壁积分。

1.2多室箱梁弯曲剪力流计算

如图2所示，建立多室薄壁箱梁截面分析模型。为了施工的方便，并使结构的受力更简洁，薄壁箱梁通常采用左右对称的截面形式，因此y轴为对称轴，亦是主轴。对于x轴的位置，设其至梁底距离为H，由静面矩Sx=∫AydA=0(其中dA为s曲线上的微面积)，可得H的计算公式如下：

(4)

式中：h为多室箱梁梁高；lc为多室箱梁翼缘板长度；tc为多室箱梁翼缘板厚度；tt为多室箱梁顶板厚度；Li为多室箱梁各箱室室宽；ti为多室箱梁各腹板厚度；td为多室箱梁底板厚度。

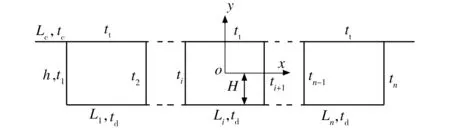
图2　多室薄壁箱梁截面分析模型

Fig.2 Model for analyzing multichambered thin-walled box girder section

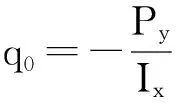
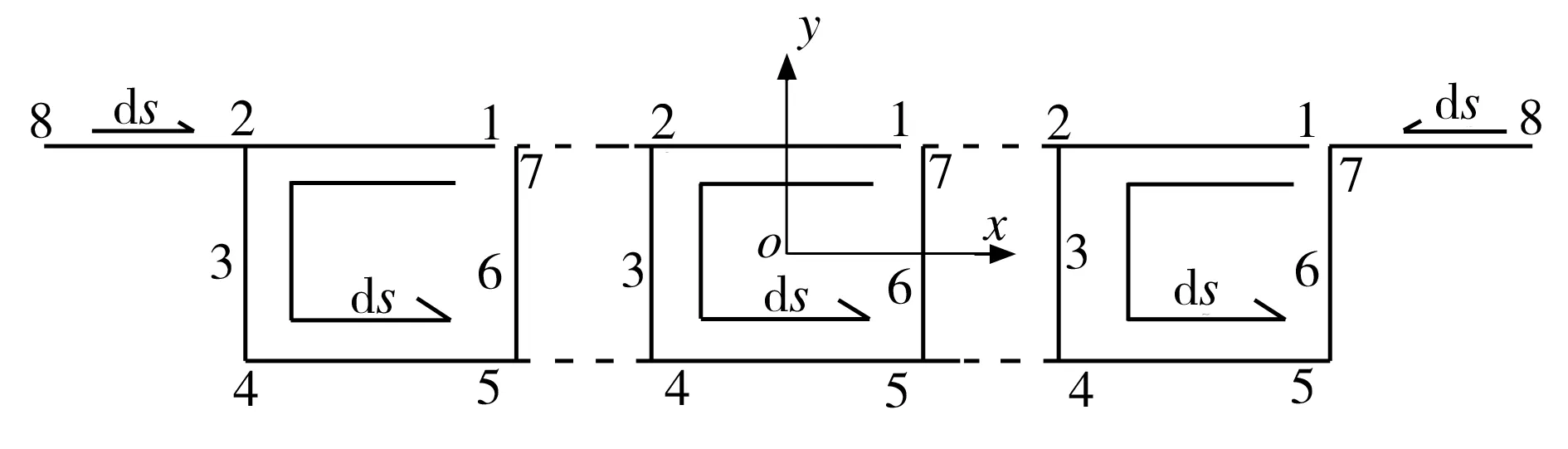
图3　开口薄壁结构

图4　静面矩Sx(s)

根据式(3)，可求得多室薄壁箱梁的位移协调方程组如下：

第1室:

(5)

第i室：

(6)

第n室：

(7)

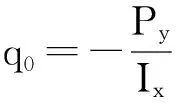
2理论公式的校核

为验证本文推导公式的正确性，选取沿x轴方向非对称的三室截面。以某三室闭口焊接箱形钢梁为例进行计算，其断面示意图如图5所示。该箱梁断面梁高180 cm，全梁总宽900 cm，其中第一室宽度为300 cm，第二室宽度为360 cm，第三室宽度为240 cm。为方便计算分析，假定在截面剪切中心作用竖向荷载Py，且Py=Ix。

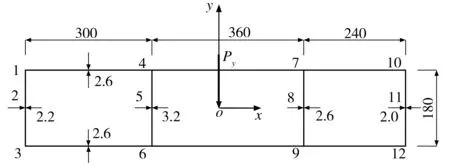
图5　三室箱梁断面示意图

利用有限元软件Midas建立该断面的有限元分析模型，单元形式为2D板单元，网格线尺寸控制为20 cm，共5085个节点，5041个单元。采用悬臂方式进行加载计算，即在梁体一侧端部固结，另一侧断面假定为平截面变形。通过在该侧截面剪切中心处建立刚域(主节点为截面剪切中心，辅节点为截面各点)，保证截面各点的旋转和位移与剪切中心保持一致，并在剪切中心处加载内力，进行线性静态分析，结果如图6所示。

将本文理论公式计算结果(以下简称“理论值”)与有限元分析的结果(以下简称“有限元值”)及文献[12]中的计算结果(以下简称“文献值”)进行对比，如表1所示。由表1可见，采用本文理论公式计算的弯曲剪力流与文献[12]中的计算结果基本相同，最大相对误差不超过5.18%；而与有限元分析结果的最大误差虽然达到了10.13%，但这可能是由于本算例中选取的是非对称截面，有限元分析中在截面剪切中心处加载内力时手动添加剪切中心造成误差，导致有限元分析时不仅计算了弯曲剪应力还考虑了扭转产生的剪应力。综上分析可知，本文推导的计算公式有较好的精度。

图6　弯曲剪力流云图

表1　三室箱形梁弯曲剪力流计算结果比较

3截面参数对剪力流的影响

选取三箱室对称薄壁梁的断面为基础分析截面，断面梁高180 cm，全梁总宽900 cm，三箱室室宽均为300 cm，悬臂板宽为200 cm，悬臂板、各箱室顶底板及腹板厚度均为10 cm。

在分析截面的基础上对截面参数作如下调整：①截面形式调整：考虑悬臂板和忽略悬臂板(以下简称“有悬臂”和“无悬臂”)；②截面厚度调整：悬臂板厚度tc与顶板厚度tt之比k1、底板厚度td与顶板厚度tt之比k2、中腹板厚度t2与边腹板厚度t1之比k3、边腹板厚度t1与中腹板厚度t2之比k4；③室宽的调整：边室室宽L2与内室室宽L1之比k5；④梁高的调整：调整后的梁高h′与原有断面梁高h之比k6。k1～ k6的取值均为1.0∶1，1.1∶1，1.2∶1，…，2.0∶1。

运用本文计算公式对本算例中的三室箱梁截面参数进行理论计算和仿真分析，仅考虑有无悬臂而其余参数不变时三室箱梁的弯曲剪力流及剪力流分配比如表2所示，有悬臂且其余参数调整后三室箱梁的剪力流分配比变化曲线如图7所示。

由表2中可得，不考虑悬臂板时，边腹板剪力流分配率相对于考虑悬臂板时的分析结果有所降低，理论值降低了5.4个百分点，有限元值降低了3.9个百分点。由此可见，为确保结构受力分析的准确性，应保证计算模型中结构的完整性。

由图7中计算可得，在参数比例调整范围内，k1、k2、k3、k4、k5、k6每增大10%，对应的剪力流分配比变化率分别为-1.5%、-0.7%、+2.6%、-2.3%、-1.3%和-0.5%，可见箱室腹板厚度、悬臂板厚度及箱室室宽对多室薄壁箱梁腹板剪力流分配的影响较大，为多室薄壁腹板剪力流分配比的主要敏感参数，而梁高与底板厚度为次要敏感参数。为确保多室箱梁腹板受力的合理性，须优化设计各箱室腹板的厚度及室宽。

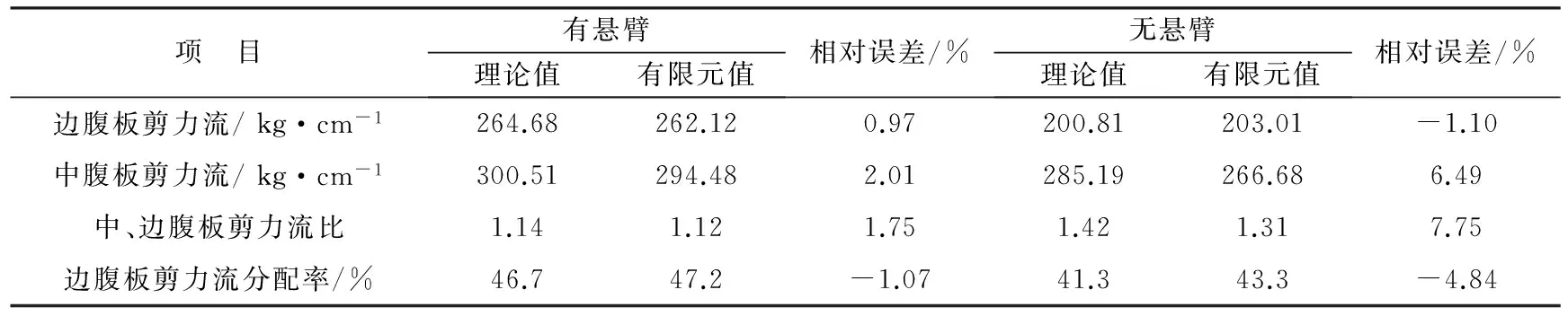
表2　三室箱梁弯曲剪力流分配比

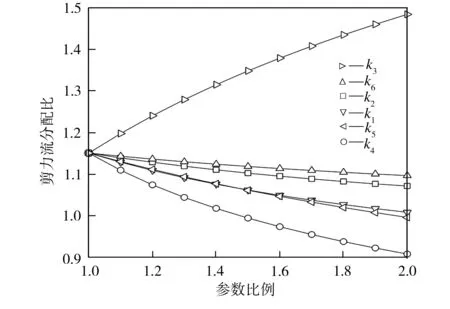
图7　剪力流分配比随参数比例的变化

Fig.7 Change of shearing flow distribution ratio with parameter ratio

4结论

(1)本文推导的多室薄壁箱梁弯曲剪力流计算公式具有较高的精度，可用于多室薄壁箱梁弯曲剪应力的理论分析。

(2)腹板厚度、悬臂板厚度及箱室宽度为多室薄壁腹板剪力流分配比的主要敏感参数，梁高与底板厚度为次要敏感参数。

(3)在桥梁结构受力分析中，为简化计算而不考虑悬臂板，会降低边腹板的荷载分配比，导致横隔梁的设计安全系数下降。

参考文献

[1]宋光吉.双对称截面薄壁杆件的斜弯曲剪力流叠加原理[J].力学与实践,2013,35(6):77-79.

[2]聂建国，李法雄.考虑腹板剪切行为的波形钢腹板梁理论模型[J].中国公路学报，2011，24(6):40-48.

[3]王忠义，张群会.平方根法在截面剪力流计算中的应用[J].西安科技学院学报，2000，20(2):185-187,192.

[4]王全凤，李华煜.薄壁杆件在纯弯下屈曲的样条有限杆元法[J].华侨大学学报：自然科学版,1996,17(2):148-156.

[5]丁强.箱梁抗剪承载力与腹板剪力分配规律的研究[D].西安:长安大学,2012.

[6]苏继宏，周军生，陈炜.多室薄壁箱梁腹板剪力分配规律分析[C]∥中国公路学会桥梁和结构工程分会.2004年全国桥梁学术会议论文集.北京：人民交通出版社，2004.

[7]张映高.多室薄壁箱梁腹板剪力分配规律初探——以河南太澳互通主线桥为例[D].南京:南京林业大学,2006.

[8]张旭慧.有限元法在箱梁剪力流分析中的应用[J].公路交通科技：应用技术版,2014(9):238-240.

[9]包世华，周坚.薄壁杆件结构力学[M].北京:中国建筑工业出版社,2006.

[10]Gjelsvik A.薄壁杆件理论[M]. 何福照，樊勇坚,译.北京:人民交通出版社,1987:98-114.

[11]郝圣旺,李慧剑,黎振兹,等.紧凑四点剪切砼Ⅱ型断裂实验研究与数值分析[J].工程力学，2003(2):138-141.

[12]黄剑源.薄壁结构的扭转分析[M].北京：中国铁道出版社,1983:26-48.

[责任编辑郑淑芳]

Calculation of bending shearing flow of multichambered thin-walled box girder web and its section parameter analysis

WangQiang,JiangTianhua，ZouYao,SunJie

(School of Urban Construction, Wuhan University of Science and Technology, Wuhan 430065, China)

Abstract:Based on structural mechanics of thin-walled bar, the formula for calculating the bending shear flow of the multichambered thin-walled box girder web was derived and applied to the calculation of steel box girder. The accuracy of the formula was testified by comparison with the results of finite element and existing literature. The influences of presence of cantilever slab, cantilever slab thickness, beam height, web thickness, bottom board thickness, chamber width on shear flow distribution were also investigated. The results show that the derived formula is very accurate, and the parameters that significantly influence shear flow distribution are web thickness, cantilever slab thickness and chamber width, while beam height and bottom board thickness have less significant influence. This suggests, in stress analysis of bridge structures, the load distribution ratio of side web would be reduced and the safety of the horizontal beam cannot be guaranteed if no consideration were given to cantilever slab or even force transfer on middle and side web were assumed.

Key words：thin-walled bar; multichambered thin-walled box girder; shear flow; finite element

收稿日期：2015-12-07

基金项目：湖北省自然科学基金资助项目(2014CFB823).

作者简介：王强(1991-)，男，武汉科技大学硕士生.E-mail：15527256827@163.com通讯作者：姜天华(1971-)，男，武汉科技大学教授，博士.E-mail：wustjth@sohu.com

中图分类号：U441

文献标志码：A

文章编号：1674-3644(2016)02-0140-05