求解随机型双边装配线平衡问题的混合回溯搜索优化算法
吴 意,唐秋华,张利平, 何晓霞
(1. 武汉科技大学机械自动化学院,湖北 武汉,430081;2. 武汉科技大学理学院,湖北 武汉,430065)
求解随机型双边装配线平衡问题的混合回溯搜索优化算法
吴意1,唐秋华1,张利平1, 何晓霞2
(1. 武汉科技大学机械自动化学院,湖北 武汉,430081;2. 武汉科技大学理学院,湖北 武汉,430065)
摘要:针对现实生产中普遍存在的操作时间为随机的双边装配线平衡问题,提出一种混合回溯搜索优化算法。该算法将变邻域搜索算法的局部搜索能力融入到回溯搜索优化算法的全局搜索中,从而实现广度搜索和深度搜索的平衡。运用基于随机键的编码将用于求解连续问题的回溯搜索优化算法应用于离散组合优化问题,同时提出一种基于均衡双边负载的边选择策略和减少工位空闲时间的任务选择策略的解码方法,并将该方法同另外4种解码方法进行对比,以验证其优越性。标杆算例测试表明,所提出的算法具有可行性和有效性。
关键词:随机型双边装配线;装配线平衡问题;回溯搜索优化算法;变邻域搜索算法;混合算法
与传统的单边装配线相比,双边装配线可以缩短装配线长度、提高工具夹具利用率、减少设备投资和维护成本、减少物料搬运、提高工人工作效率[1],故被广泛应用于汽车、装载机等大型产品的装配。平衡装配线的工位负载,可以极大提高生产效率和资源利用率,也导致装配线平衡成为装配线规划和设计过程中的首要问题。根据求解目标的不同,双边装配线平衡问题可以分为TALBP-Ⅰ和TALBP-Ⅱ两类子问题,其中TALBP-Ⅰ是已知节拍,最小化工位数目,而TALBP-Ⅱ是已知工位数目,最小化生产节拍。
1993年Bartholdi[1]首次提出了双边装配线平衡问题的概念,并且给出了一种基于优先匹配原则的启发式平衡算法。此后许多学者对双边装配线平衡问题进行了研究。Hu等[2]提出了一种面向工位的枚举算法来求解双边装配线平衡问题。Wu等[3]提出了分支定界算法解决双边装配线平衡问题。Kim等[4]提出了一种基于“工位”编码方式的遗传算法,解决了具有位置约束的第一类装配线平衡问题。Lee等[5]对双边装配时任务的相关度和任务安排的松弛度进行了研究。吴尔飞等[6]提出一种基于任务排列序列的遗传算法,求解了第一类双边装配线平衡问题。Yuan等[7]运用延迟接受爬山算法解决含有位置约束、区域约束和协同约束的双边装配线平衡问题。李大双等[8]采用殖民竞争算法,求解了多约束双边装配线平衡问题。
以上研究中均假设操作时长是确定的、不改变的,而在实际装配过程中,不论是人工装配还是机器人装配,操作时间本身都带着不确定性。这些不确定因素可能导致确定条件下所求出最优平衡方案的性能衰减,甚至不可行,导致生产过程中效率降低,甚至造成生产中断。对于操作时间的变动符合某种概率分布的随机双边装配线平衡问题,Özcan[9]提出机会约束分段线性的混合整数规划模型并且采用模拟退火算法求解随机型双边装配线平衡问题;李大双等[10]采用多目标混合殖民竞争算求解了随机型双边装配线平衡问题。
从上述研究现状可以看出,目前大多数研究者主要致力于确定型的双边装配线平衡问题,对于现实制造环境中广泛存在的随机装配线的平衡问题研究较少。针对以上问题,本文提出一种混合回溯搜索优化算法,该算法结合回溯搜索优化算法的全局能力和变邻域搜索算法的局部搜索能力,以期实现搜索深度和广度间的平衡。同时提出一种均衡各工位任务负载和减少序列相关所引起的空闲时间的解码策略。
1随机型双边装配线平衡问题
双边装配线是在单边装配线的基础上,将原本的单一生产线分为左右两条线,任务在装配线的左右两侧并行装配。在传送带左右两侧,面对面的两个工位称为成对工位,两工位间彼此称为伴随工位。
装配线平衡问题可用如图1所示的优先关系图表示。图1中圆圈内的数字代表任务,圆圈下边的标签(ti,di)代表完成任务所需的时间和方向,箭头表示任务之间的优先关系。对任务来说,有些仅能在双边装配线的左边完成,用L表示;有些仅能在双边装配线的右边完成,用R表示;还有些可以在任一边完成,称为E。在双边装配线平衡时必须考虑由于序列相关所导致的空闲时间。如果一对具有优先关系约束的任务被分配到同一个成对工位的两边,则后续任务必须等待其伴随工位中的前序任务完成之后才能开始操作,因此有可能产生序列相关空闲时间。
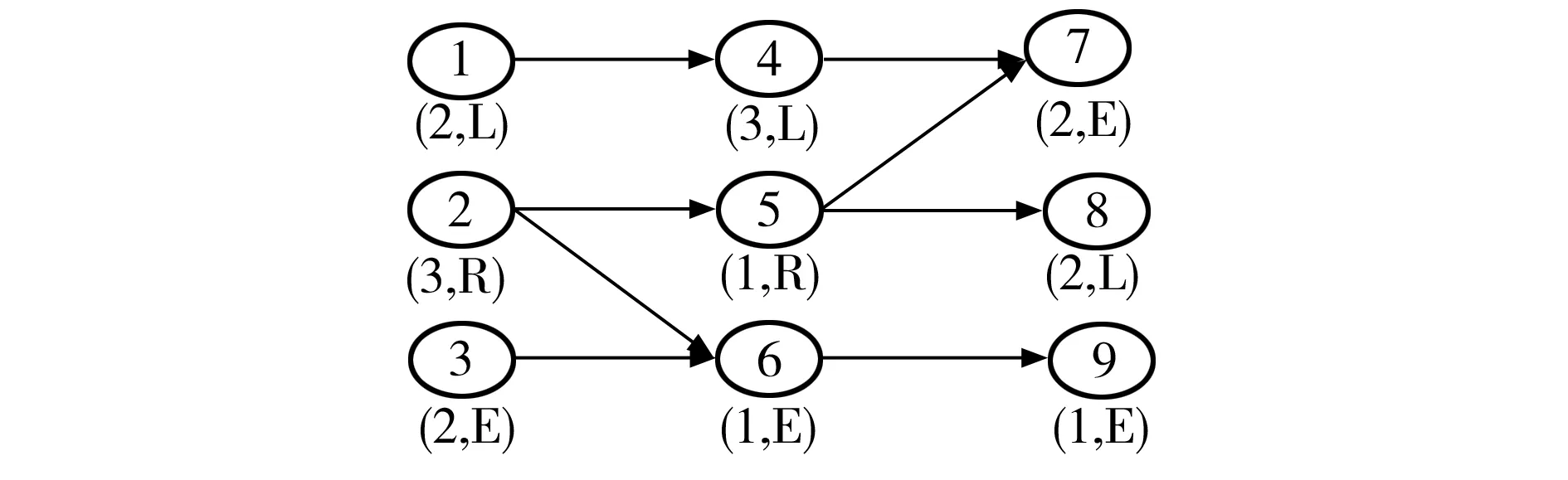
图1 双边装配线优先关系图
2基于混合回溯搜索优化算法的随机型双边装配线平衡
回溯搜索优化算法(Backtracking Search Optimization Algorithm,BSA)是Civicioglu于2013年提出的一种新的进化算法[11]。该算法只有一个控制参数,操作简单。同时,在优化过程中通过产生实验种群、调整搜索方向和搜索边界,使算法具有可快速、有效收敛的优势。鉴于其良好的优化性能,BSA已成功用于求解置换流水车间调度问题[12],本文是首次将其应用于求解随机型TALBP-Ⅰ问题。
BSA算法共分为种群初始化、选择Ⅰ、变异、交叉和选择Ⅱ5个部分。为提高BSA的局部搜索能力以获得更优解,本文提出将变邻域搜索加入到BSA中,形成混合BSA(HBSA)算法,其总体框架如图2所示。
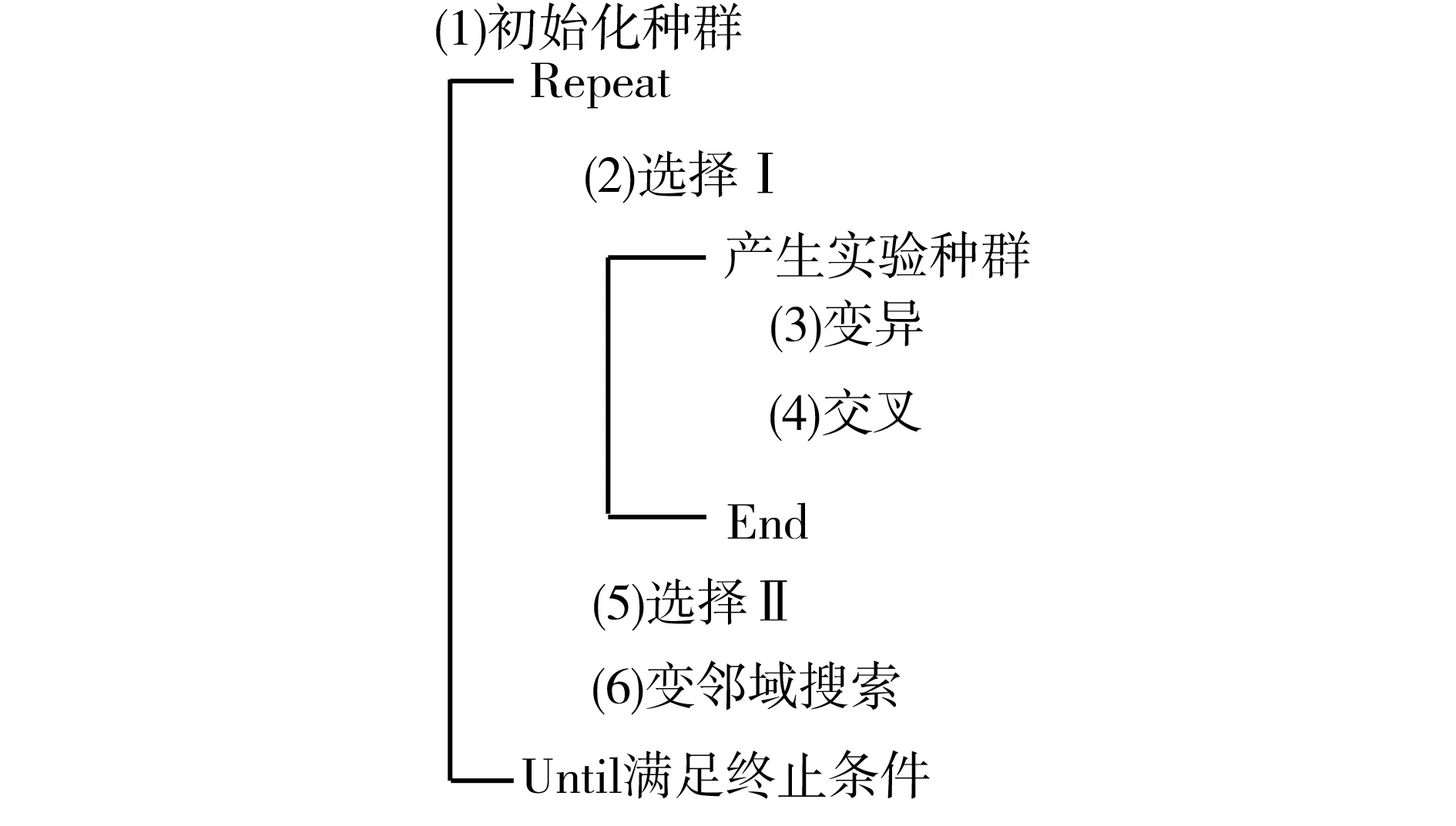
图2 HBSA算法总体框架
2.1编码和初始化
BSA采用随机方法进行种群初始化,如下式所示:
Pi,j~U(lowj,upj)
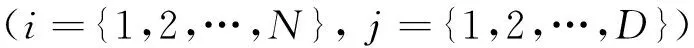
(1)
式中:P为种群;N和D分别表示种群规模和问题维度;lowj和upj分别为搜索空间中第j维的下界和上界;U表示随机均匀分布函数。
随机型双边装配线平衡问题是典型的离散组合优化问题,但BSA算法更适用于求解有边界值的连续问题。为了使BSA算法能用于求解离散问题,借鉴Bean[13]的随机键编码方法产生任务序列。该方法具体为:将算法的维度对应于装配任务数,为每个任务生成0~1之间的随机数,随机数的大小表示任务的优先级,随机数越小,优先级越高,在任务序列中优先分配。以图1所示的9个任务为例,对其产生如表1所示的9个[0,1]之间的随机数。由表1中可见任务3对应的随机数最小,排在任务排序的第一位,依此类推,获得9个任务的排序为:{3,1,4,2,6,5,9,7,8}。

表1 随机键编码
2.2解码
基于随机键的编码可以获得一组任务排序,但是该任务排序仅指明在分配过程中各任务的优先权,还需要进一步解码来获得可行解。
针对双边装配线平衡,常用的启发式解码策略是直接选择待分配任务。为促进装配线同一成对工位两边的负载均衡,提出先选边、再选任务的解码策略,其解码思想是:首先为当前成对工位的左右两边同时产生两组候选任务集,然后优先选择开始时间早的一边,最后从当前所选边的候选任务集中优先选择可以减少序列相关时间的任务。通过边选择策略可以均衡工位之间的负载,通过任务选择策略可以减少任务之间序列相关闲置时间。详细解码流程如图3所示。另外,在不违反节拍约束和方向约束的条件下,最后的成对工位可合并为一个工位,以减少工位数量。
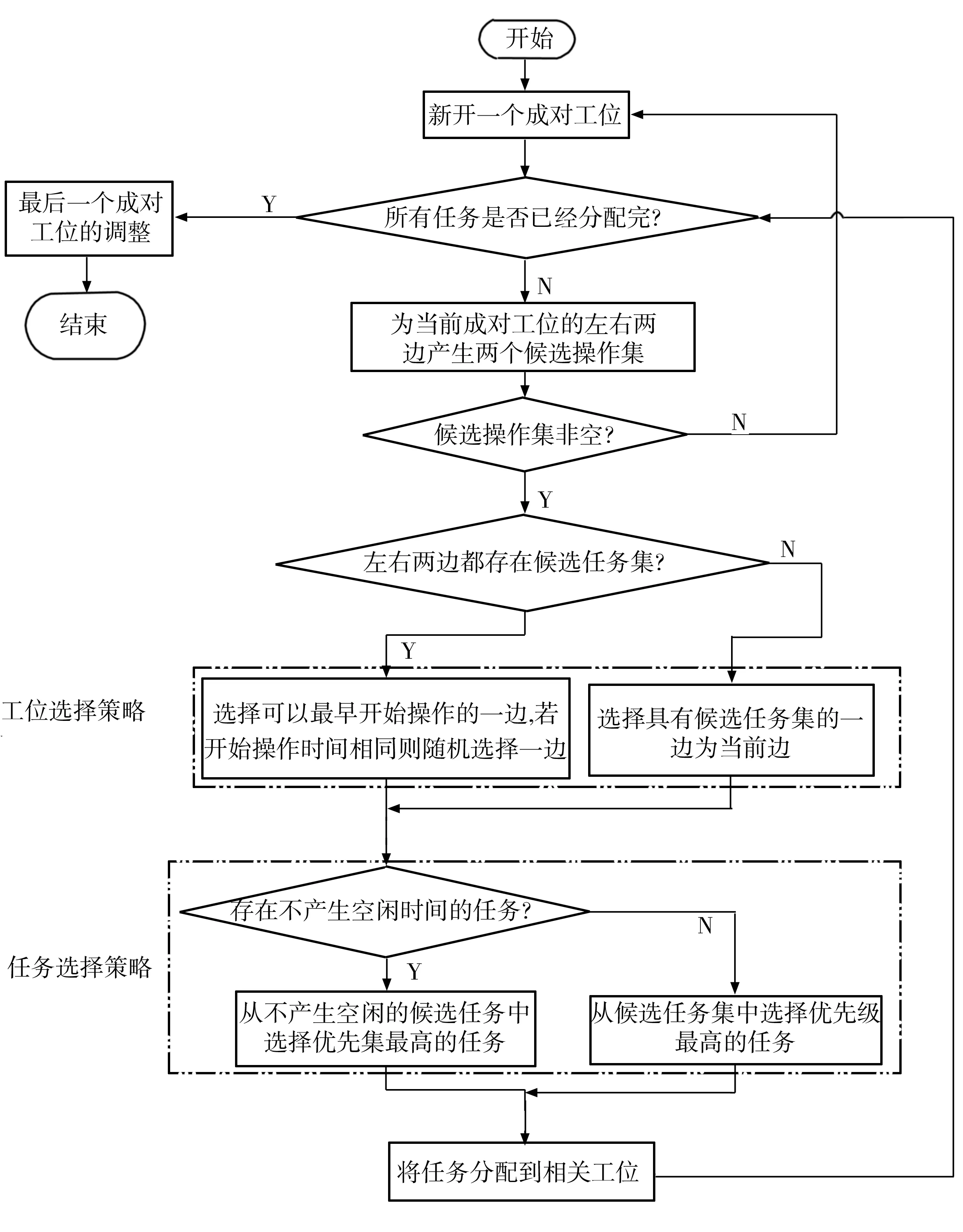
图3 解码流程
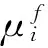
(2)
式中:Φ-1(α)为分布函数在概率值为α时所对应的值。
分析式(2)可知,若要任务完成时间百分百满足节拍约束,则会导致节拍无穷大。实际上,每个操作完成时间接近最大实际完成时间的概率极小,并无必要强制要求节拍大于最大实际完成时间,故仅强制各工位以概率α满足节拍约束。换言之,允许各工位以(1-α)的概率违背节拍约束,在实际生产中遇到此类情形时,采用停机方式处理。上述思想可用下式表示:
(3)
式中:CT为节拍;I为任务集。
2.3适应度函数
由于求解的是第一类装配线平衡问题,用下式作为目标函数,以缩短生产线的长度:
(4)
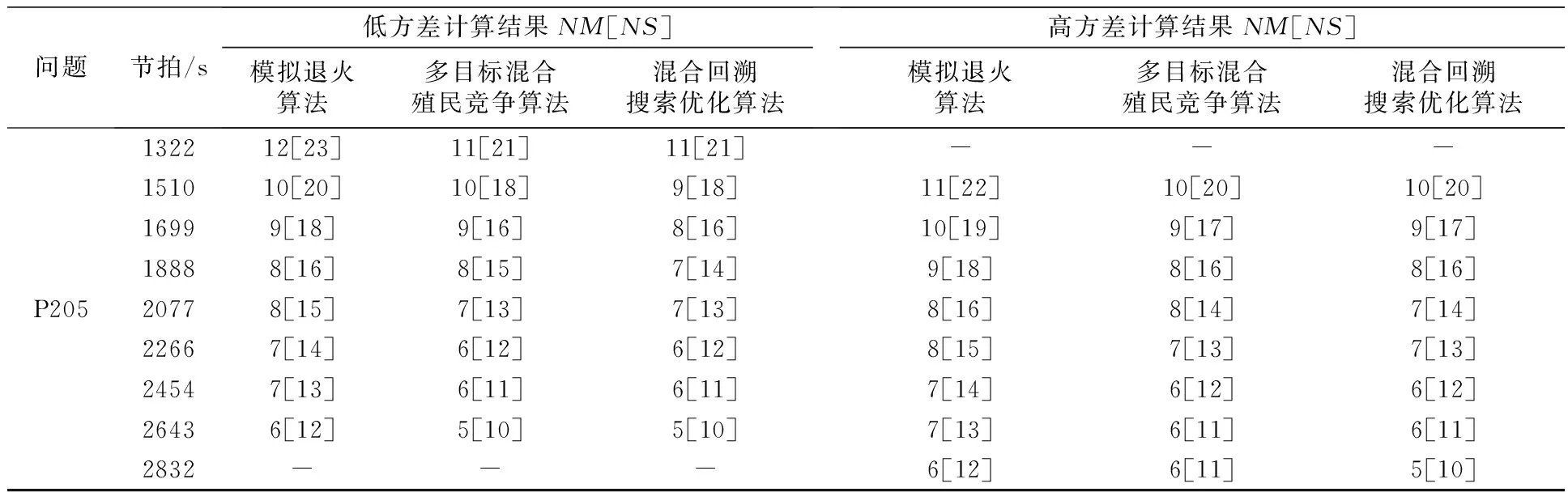
式中:NM表示成对工位数量;NS表示总工位数量;wnm和wns为系数,考虑到一个成对工位包含两个工位,令其分别取值2和1。
2.4选择Ⅰ
设计选择Ⅰ算子的目的是对种群进行筛选,以构造新的历史种群OldP,具体如下式所示:
ifa (5) 式中:a,b为(0,1)上服从均匀分布的随机数。 利用式(5),可从前代种群中随机性地记忆某个历史种群,直至历史种群再次发生改变。并且在历史种群OldP确定之后,对OldP中各个体的位置进行随机排列。 通过对历史种群的这一操作,实现算法对种群位置的记忆功能。同时,利用历史种群与当前种群的差别,还可作为搜索方向,进一步指导搜索过程。 2.5变异 通过下式执行变异操作,生成初始实验种群Mutant: Mutant=P+F(OldP-P) (6) 式中:F为控制搜索方向矩阵OldP-P幅度的参数,F=3rand,其中rand为[0,1]上服从正态分布的随机数。 2.6交叉 交叉过程产生最终的实验种群T。实验种群T的初始取值为变异过程产生的Mutant。BSA算法中提出了一种新的种群交叉策略。该交叉策略的第一步是根据下式计算N×D的二元整数矩阵map: (7) 式中:a、b为[0,1]上的随机数;mixtrate为混合比例参数;randi(D)表示在[0, D]中随机取一个整数;u为随机排序后的整数向量,u∈[1,2,…,D]。 map的初始值为1,采用式(7)的两种方式来定义map的取值:当a 第二步是根据map的取值采用下式更新实验种群T: (8) 2.7选择Ⅱ 通过贪婪选择机制在新种群T与初始种群P中选择目标值较好的种群个体,并记录当前最优解和对应的解向量,同时更新初始种群,完成一次迭代。 2.8变邻域搜索 (1)交换(N1):随机选择两个任务,交换两个任务在操作序列的位置。 (2)多交换(N2):将交换操作执行两次。 (3)后插(N3):随机选择两个任务,将前面的任务插入到另一个任务的后面。 (4)前插(N4):随机选择两个任务,将后面的任务插入到另一个任务的前面。 (a)交换 (b)多交换 (c)后插 (d)前插 设计图5所示的算法流程,可交替使用4种邻域结构,拓宽局部搜索的范围。 图5 VNS伪代码 3算例分析 混合回溯搜索优化算法采用 C++语言编程,在电脑CPU为Intel(R) Core5(TM) CPU 3.1 GHz, 8 GB内存的Microsoft Visual Studio 2010 平台下运行。为了验证所提出的启发式解码和混合回溯搜索优化算法的优越性能,首先对启发式解码方法进行了对比,然后将计算结果同现有文献的计算结果进行对比。对基准问题P65[5]、P148[1]和 P205[5]进行测试,任务的方差(包含高方差和低方差)及其他数据与文献[9]一致,概率值α设定为0.9,相对应的正态分布函数值为1.28。 3.1解码对比 本研究中,在启发式解码中采用的任务选择策略是优先选择不产生空闲时间的任务(EBT)。为了说明这种任务选择策略的优越性,将其与以下几种不同的任务选择策略组成的解码方式进行对比:①选择后续任务操作时间总和最长的任务(MAX-TTST);②选择具有最多直接后续作业数的任务(MAX-IFOL);③选择有最多后续作业数的任务(MAX-TFOL);④选择有最大位置权重的任务(MAX-RPW),位置权重是指该任务及该任务所有后续任务的操作时间的和。 将5种解码方式分别对P148低方差进行求解,每组求解10次。采用相对百分率偏差 (Relative Percentage Deviation, RPD)比较不同解码方式获得解的质量: (9) 式中:Somesol表示采用任意一种解码方式获得的工位数;Best表示所有解码中的最优工位数。 同时,用方差分析(Analysis of Varicance, ANOVA)来统计分析不同解码方式获得解的质量,其中解码作为自变量。在95%最小显著差数间隔的置信水平下,5种任务选择策略解码的均值如图6所示。从图6中可以看出,本文所提出的解码方式EBT性能最优。 图6 解码平均值对比 3.2计算结果对比 为了验证混合回溯搜索优化算法的有效性,本文将该算法同Özcan[9]提出的模拟退火算法及李大双[10]提出的多目标混合殖民竞争算法进行对比。每个案例独立运行10次,取最好的结果。算法的参数设置为:种群规模为50;混合比例参数mixtrate设置为1,算法终止条件为运行时间t=n×n×10 ms,n为任务数。运行结果对比如表2所示。 从表2可以看出,对基准问题P65、P148和 P205,混合回溯搜索优化算法取得了当前所有的最优解。同时,混合回溯搜索优化算法还更新了以下7个最优值:在低方差的计算结果中,P148(CT=357)和P205(CT=1888)减少了1个成对工位和1个工位;P205(CT=1510、1699)减少了1个成对工位;P148(CT=510)减少了1个工位;在高方差的计算结果中,P205(CT=2077)减少了1个成对工位,而P205(CT=2832)则同时减少了1个成对工位和1个工位。由此可见,混合回溯搜索优化算法能够有效求解随机型双边装配线平衡问题,对实际生产中减少工位数、降低成本具有重要指导意义。 表2 计算结果对比 续表 问题节拍/s低方差计算结果NM[NS]模拟退火算法多目标混合殖民竞争算法混合回溯搜索优化算法 高方差计算结果NM[NS]模拟退火算法多目标混合殖民竞争算法混合回溯搜索优化算法P205132212[23]11[21]11[21]---151010[20]10[18]9[18]11[22]10[20]10[20]16999[18]9[16]8[16]10[19]9[17]9[17]18888[16]8[15]7[14]9[18]8[16]8[16]20778[15]7[13]7[13]8[16]8[14]7[14]22667[14]6[12]6[12]8[15]7[13]7[13]24547[13]6[11]6[11]7[14]6[12]6[12]26436[12]5[10]5[10]7[13]6[11]6[11]2832---6[12]6[11]5[10] 4结语 本文首次将回溯搜索优化算法应用到装配线平衡问题的求解中,并且针对随机型双边装配线平衡问题,提出了一种混合回溯搜索优化算法。该算法利用随机键进行初始化,并且将变邻域搜索算法的局部搜索能力同回溯搜索优化算法的全局搜索能力相结合,在算法的搜索深度和广度之间取得了较好平衡。同时,针对双边装配线的独有特性,即任务序列相关性会导致工位空闲时间,提出了一种均衡工位之间负载和减少序列相关空闲时间的解码方法。通过不同方式的解码对比,并采用方差分析验证了所提出解码方法的优越性。标杆案例测试表明,该算法获得了全部的当前最优解,且更新了7个最优值,表明其具有可行性和有效性。 参考文献 [1]Bartholdi J J. Balancing two-sided assembly lines: a case study[J]. International Journal of Production Research, 1993, 31(10): 2447-2461. [2]Hu X F, Wu E F, Jin Y. A station-oriented enumerative algorithm for two-sided assembly line balancing[J]. European Journal of Operational Research, 2008, 186(1): 435-440. [3]Wu E F, Jin Y, Bao J S, et al. A branch-and-bound algorithm for two-sided assembly line balancing[J]. International Journal of Advanced Manufacturing Technology, 2008, 39: 1009-1015. [4]Kim Y K, Kim Y, Kim Y J. Two-sided assembly line balancing: a genetic algorithm approach[J]. Production Planning and Control, 2000, 11(1): 44-53. [5]Lee T O, Kim Y, Kim Y K. Two-sided assembly line balancing to maximize work relatedness and slackness[J]. Computers and Industrial Engineering, 2001, 40(3): 273-292. [6]吴尔飞,金烨,续爱民,等. 基于改进遗传算法的双边装配线平衡[J].计算机集成制造系统, 2007,13(2):268-274. [7]Yuan B, Zhang C Y, Shao X Y. A late acceptance hill-climbing algorithm for balancing two-sided assembly lines with multiple constraints[J]. Journal of Intelligent Manufacturing, 2015, 26(1): 159-168. [8]李大双, 张超勇, 邵新宇, 等. 基于殖民竞争算法的多约束双边装配线平衡[J]. 机械工程学报, 2015, 51(2): 183-189. [9]Özcan U. Balancing stochastic two-sided assembly lines:a chance-constrained, piecewise-linear, mixed integer program and a simulated annealing algorithm [J]. European Journal of Operational Research, 2010, 205 (1): 81-97. [10]李大双,张超勇,邵新宇,等. 基于多目标殖民竞争算法的随机型双边装配线[J]. 计算机集成制造系统, 2014, 20(11): 2774-2787. [11]Civicioglu P. Backtracking search optimization algorithm for numerical optimization problems[J]. Applied Mathematics and Computation, 2013, 219(15): 8121-8144. [12]Lin Q, Gao L, Li X Y, et al. A hybrid backtracking search algorithm for permutation flow-shop scheduling problem[J]. Computers and Industrial Engineering, 2015, 85: 437-446. [13]Bean J C. Genetic algorithms and random keys for sequencing and optimization[J].ORSA Journal on Computing, 1994, 6(2): 154-160. [责任编辑郑淑芳] Solving stochastic two-sided assembly line balancing problem via hybrid backtracking search optimization algorithm WuYi1,TangQiuhua1,ZhangLiping1,HeXiaoxia2 (1.College of Machinery and Automation, Wuhan University of Science and Technology, Wuhan 430081, China;2. College of Science, Wuhan University of Science and Technology, Wuhan 430065, China) Abstract:In this paper, a hybrid backtracking search optimization algorithm (HBSA) is proposed to solve the widespread stochastic two-sided assembly line balancing problem. The local search ability of the variable neighborhood search (VNS) is integrated into the global search ability of backtracking search optimization algorithm (BSA) so as to make the balancing between diversification and intensification. The random-key based encoding scheme is employed for successfully applying BSA which is originally proposed for continuous problem to discrete combinatorial optimization problem. A decoding scheme which is based on side and task selection strategies is used to balance the workload between workstations and reduce idle time related to sequence-dependence. And the performance of the proposed decoding scheme is demonstrated by comparison with four other decoding schemes which are based on different heuristic task selection strategies. The corresponding benchmark experiment results demonstrate that the proposed algorithm can solve the problem effectively. Key words:stochastic two-sided assembly line; assembly line balancing problem; BSA; VNS; hybrid algorithm 收稿日期:2015-12-22 基金项目:国家自然科学基金资助项目(51275366,51305311,11201356). 作者简介:吴意(1990-),男,武汉科技大学硕士生.E-mail:wuyiwust@126.com通讯作者:唐秋华(1970-),女,武汉科技大学教授,博士生导师.E-mail:tangqiuhua@wust.edu.cn 中图分类号:F403.7 文献标志码:A 文章编号:1674-3644(2016)02-0121-07