基于ART和Yu范数的聚类方法在齿轮故障诊断中的应用

徐增丙，李友荣，王志刚，轩建平

(1.武汉科技大学机械自动化学院，湖北 武汉，430081;2.华中科技大学机械科学与工程学院，湖北 武汉，430074)



基于ART和Yu范数的聚类方法在齿轮故障诊断中的应用

徐增丙1，李友荣1，王志刚1，轩建平2

(1.武汉科技大学机械自动化学院，湖北 武汉，430081;2.华中科技大学机械科学与工程学院，湖北 武汉，430074)

摘要：针对传统聚类方法需预先指定类别个数而导致应用受限的问题，提出一种基于ART和Yu范数的聚类方法，可自适应地确定类别个数。通过对齿轮无标记故障样本的诊断分析对该方法进行验证。从多个角度提取反映故障信息的特征参数集，利用距离区分技术对其进行优选，并结合ART的机制和基于Yu范数的聚类技术，对齿轮故障类别进行诊断分析，并与Fuzzy ART方法的诊断结果进行比较。结果表明，该方法可以有效地对齿轮故障进行区分，且效果优于Fuzzy ART方法。

关键词：齿轮；故障诊断；聚类方法；ART；Yu范数；距离区分技术

故障诊断的本质就是模式识别[1]，即通过采集的原始数据对设备的故障状态进行识别和区分。在实际的工业生产过程中，往往只有故障数据样本，无对应的故障类别，因此如何对这些数据样本进行区分已成为设备故障诊断的关键，聚类技术则成为解决该类问题的重要方法之一[2]。聚类方法主要是利用距离或相似测度对数据样本进行分类，目前常用的聚类方法如KNN、K均值等已广泛应用于轴承、齿轮的故障诊断之中[3-4]。虽然这些方法具有知识存储、自学习等功能，但需事先指定聚类个数以及初始化聚类中心，严重影响其诊断精度。而基于自适应共振理论(ART)发展起来的系列神经网络模型如ART1、ART2、Fuzzy ART等则可很好地解决这些聚类方法常遭受的“适应性”与“稳定性”两难困境[5-7]，但受样本输入顺序的影响导致其应用受限[8]。

在实际的故障诊断过程中，由于故障边界的模糊性常导致边界处对应的数据样本难以准确区分，而模糊理论则可以很好地解决此问题。2007年芬兰学者Luukka[9]在模糊理论的基础上，提出了一种利用Yu范数进行相似性测度分析的分类方法，并将其运用于医疗数据的分类之中，效果较好，但在机械系统故障诊断的应用研究方面尚未见公开报道。

为此，本文将自适应共振理论(ART)和基于Yu范数的相似性聚类方法相结合，提出一种基于ART和Yu范数的ART-Yu聚类模型，并结合基于距离区分技术的特征参数优化方法，对齿轮故障进行诊断分析。

1诊断流程

基于ART和Yu范数聚类方法的故障诊断流程如图1所示。运用信号处理方法从原始振动信号中提取反映故障信息的特征参数，运用距离区分技术对其进行优选，并将选取的敏感特征参数作为ART-Yu聚类模型的输入，从而对机械设备故障状态进行分类。

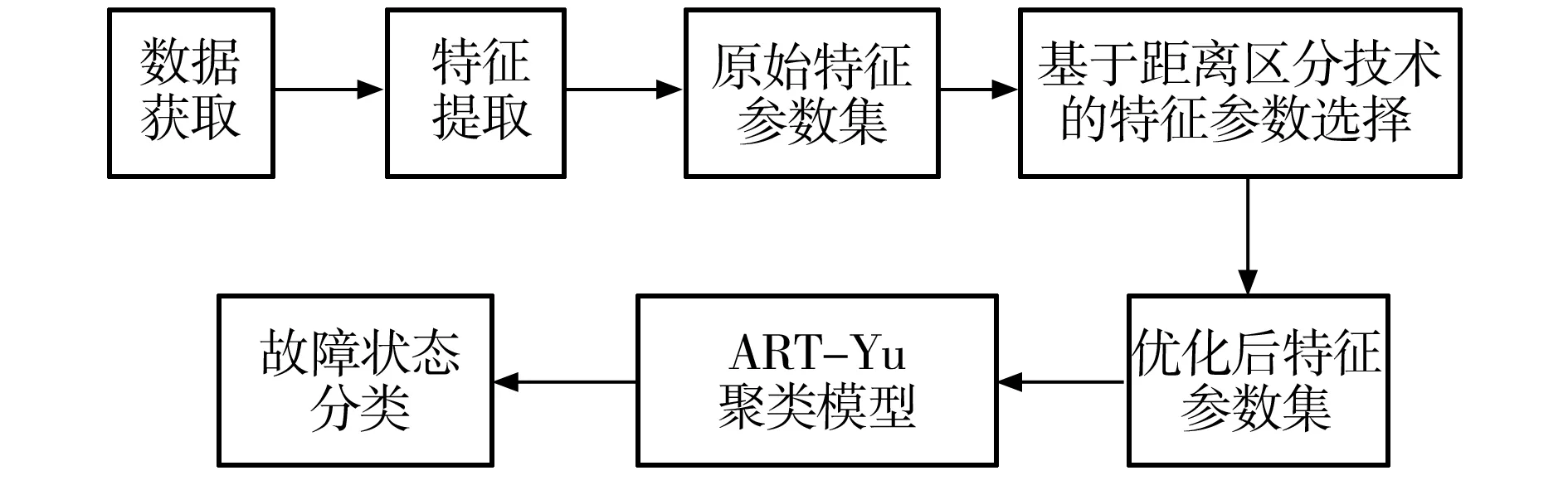
图1　基于ART-Yu聚类模型的故障诊断流程图

Fig.1 Flowchart of fault diagnosis based on ART and Yu clustering model

2特征参数提取及优选

2.1特征提取

特征参数常用来描述机械系统的故障状态信息。为获取更多的信息，选取均值、均方根值、标准方差3个有量纲特征和偏度、峭度、波峰因子、裕度因子、波形因子、冲击因子等6个无量纲特征作为反映机械系统状态的时域信息；选取平均频率、平均频度、波形稳定因子、变化系数、频域偏度、频域峭度等特征参数作为反映机械系统故障状态的频域信息；并且考虑到时间序列反映着机械系统工作的动态过程，蕴含着系统的行为特征和固有特性，将振动信号的时间序列用自回归AR(p)模型参数作为反映机械系统状态的特征参数，这里选p=16。

2.2基于距离区分技术的特征参数优选

特征参数之间的冗余性或不相关性会增加计算负担、降低聚类模型的分类精度。为解决此问题，Liang[10]等提出了基于距离区分技术的特征参数优选方法，即利用特征参数的类内距离和类间距离的比例大小来评估特征参数的敏感度，若某特征参数在类内距离越小、类间距离越大，则该特征参数越敏感，具体算法如下：

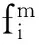
(2)计算所有样本第m个特征参数的标准方差和均值：

(1)

(2)

(3)计算第j类所有样本的第m个特征参数的标准方差和均值：

(3)

(4)

(4)计算第m个特征类中心gj的加权标准方差：

(5)

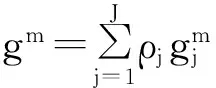
(5)计算第m个特征的距离区分因子：

(6)

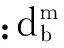
(6)按降序的方式排列变化的距离区分因子λm，并进行正则化处理得:

(7)

3ART-Yu聚类模型

3.1ART神经网络原理

ART神经网络是一种基于竞争学习机制的自组织、增量式神经网络模型[5]，既能在适应新的输入模式方面有较大的可塑性，又能避免对已学习的模式类别进行修改。其主要工作原理为：①依据输入样本与所有存储模式类别之间的相似度，利用“胜者为王”的方式选择“优胜”模式类别；②通过警戒参数检验输入样本与优胜模式类别之间的匹配度，若满足，则进入共振状态，对应的模式类别权重进行调整学习；若不满足，则产生新的模式类别。

3.2ART-Yu聚类模型的建立

在模糊逻辑领域中，于延栋教授在1985年提出的T范数和S范数被称为Yu范数，其数学表达式分别为

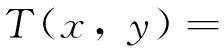
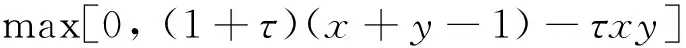
(8)

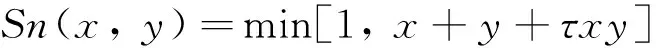
(9)

式中：x,y∈[0,1]；τ>-1。

根据该范数的特有性质，Luukka[9]利用如下等价关系式：

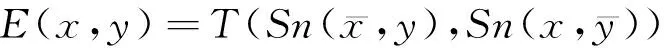
(10)

计算样本间的相似度，并依此建立了基于Yu范数的聚类模型，但该模型分类时需事先确定类别的个数，严重影响了分类精度。为此本文结合ART和Yu范数的特点，建立了ART-Yu模型，其拓扑结构如图2所示，具体算法流程如下：

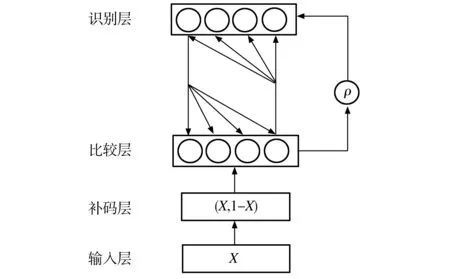
图2　ART-Yu聚类模型结构图

Fig.2 Architecture of the clustering model based on ART and Yu norm

(1)预处理。对D维输入样本矢量X进行正则化和补码编码处理。

(2)模式选择。假定有N个模式节点，代表类i的模式节点权重为Vi=(vi(1),…,vi(D))，则输入样本矢量X与各模式节点的相似度可表示为

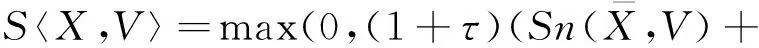
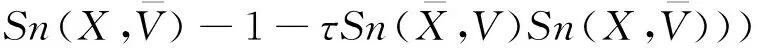
(11)

获胜的模式节点对应的最大相似度可用下式表示：

(12)

式中：J为获胜模式节点编号；VJ为其对应权重矢量。

(3)模式匹配。将最大相似度S〈X,VJ〉与警戒参数ρ进行比较，若

(13)

则表示样本X分到模式节点VJ所代表的类中，转入步骤(4)；否则重新建立一个新模式节点，转入步骤(5)。

(4)学习调整。当获胜模式节点VJ满足警戒参数ρ时，其权值需重新进行学习，即

(14)

式中：VJ0为原始权值矢量；VJ为学习后的权值矢量；n为属于模式节点J的样本个数。

(5)模式节点的建立。若输入样本X与模式节点J的权值不满足警戒参数ρ，即S〈X,VJ〉<ρ，则重新建立一个新模式节点，其权值矢量可表示为

(15)

4案例分析

运用提出的ART-Yu模型对布鲁塞尔自由大学提供的齿轮箱故障数据[11]进行了诊断分析。试验对象是模数为5 mm、齿数比为41∶37的斜齿轮副，其中41 齿齿轮轴转频为10 Hz，采样频率10 kHz。测试过程中，在41 齿齿轮上模拟了5种不同情形(正常、轻度剥落、中度剥落、严重剥落和轻度磨损)，且诊断分析时每个故障类对应的样本数均为30。

利用前面描述的特征参数提取及优化方法，从每个数据样本中提取了16个AR模型参数和9个时域特征、7个频域特征，并结合距离区分技术对其敏感度进行分析。这里设定门槛值γ为0.97，依此选取了8个敏感特征参数，包含1个AR模型参数、2个时域特征参数和5个频域特征参数，如图3所示。

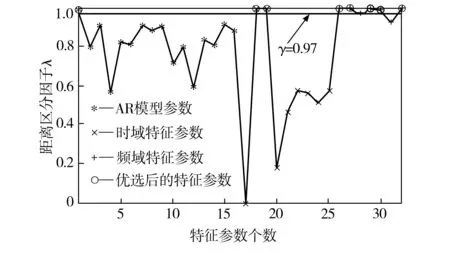
图3　特征参数选择

ART-Yu聚类模型的主要特点是可将训练和测试同时进行。在诊断开始时，模型为空，无聚类节点；当第一个样本输入模型时，便产生第一个聚类节点；第二个样本输入模型时，第一个聚类节点便与其进行相似性比较分析，若相似度满足式(13)，则该样本被分到第一个聚类节点，该节点对应的权重需重新学习，若不满足则重新生成第二个节点。其他样本的分类过程依此类推。表1给出了齿轮不同故障状态下所对应的聚类节点个数，从表1中可知，齿轮每个故障状态需由多个聚类节点来表示，这主要是因为齿轮故障的复杂机制导致振动波形多样化，引发故障样本聚类时存在多个聚类中心即聚类节点。表1数据也进一步说明，即使不同类型和不同严重程度的齿轮故障需要用多个节点进行描述，该聚类方法仍可有效地对其进行识别。

表1齿轮每个故障状态对应的节点数

Table 1 Number of cluster nodes corresponding to each fault condition

状态正常轻度剥落中度剥落重度剥落轻度磨损类标签12345节点个数24424

诊断精度是评价一个诊断模型的主要指标。这里定义诊断精度DA为

(16)

式中：C为正确分类样本个数；T为总样本数；N为聚类节点数[12]。

表2给出了不同警戒参数值的条件下该聚类方法的诊断精度和分类节点个数。从表2中可以看出，随着ρ的增大，当警戒参数ρ<0.999 995时，聚类节点个数增加，诊断精度也提高；而当ρ>0.999 995时，聚类节点个数继续增加，但诊断精度下降。这是因为当ρ增长时，代表同一故障状态的每个聚类节点在空间中所表示的区域变小，对应的节点个数随之增加；而诊断精度先提高后下降，可能是由不同故障类别的聚类节点所占据的空间区域之间的距离较近而造成。

表2　警戒参数ρ与聚类节点个数和诊断精度之间的关系

为了验证本文提出方法的优越性，采用Fuzzy ART神经网络，利用同样的数据样本对齿轮故障进行了诊断分析，对比结果如表3所示。从表3可以看出，与Fuzzy ART模型相比，当以原始的32个特征参数和优选的8个特征参数分别作为输入时，ART-Yu模型的诊断精度均较高，表明ART-Yu模型可有效地对齿轮故障进行诊断，且效果优于Fuzzy ART模型；当特征参数优选后，ART-Yu模型和Fuzzy ART模型的诊断精度均得以提高，表明采用距离区分技术对特征参数进行优选，可提高诊断模型的识别精度。

表3齿轮诊断结果的比较

Table 3 Comparison of gear fault diagnosis results with different methods

特征参数个数诊断精度/%ART-YuFuzzyART328040886.6786

5 结论

(1)本文提出的ART-Yu聚类方法可以有效地对齿轮故障进行诊断分析，且诊断性能优于Fuzzy ART，在齿轮故障诊断领域具有很好工程应用前景。

(2)距离区分技术可有效地对故障状态敏感特征参数进行优选，减少了冗余或不相关特征参数对故障类别的影响，提高了诊断精度。

参考文献

[1]屈梁生，张海军．机械诊断中的几个基本问题[J]．中国机械工程，2000，11(1-2)：211-216.

[2]王娜,杜海峰,庄健，等. 用于故障诊断的网络分割谱聚类方法[J].机械工程学报，2008,44(10):228-233.

[3]Pandya D H, Upadhyay S H, Harsha S P. Fault diagnosis of rolling element bearing with intrinsic mode function of acoustic emission data using APF-KNN[J]. Expert Systems with Applications，2013, 40(10): 4137-4145.

[4]Yiakopoulos C T, Gryllias K C, Antoniadis I A. Rolling element bearing fault detection in industrial environments based on aK-means clustering approach[J].Expert Systems with Applications, 2011, 38(3): 2888-2911.

[5]Grossberg S. Adaptive resonance theory: how a brain learns to consciously attend, learn, and recognize a changing world[J]. Neural Networks, 2013, 37(1): 1-47.

[6]Carpenter G A, Grossberg S, Rosen D B. Fuzzy ART: fast stable learning and categorization of analog patterns by an adaptive resonance system[J].Neural Networks,1991, 4(6): 759-771.

[7]Carpenter G A，Grossberg S. ART 2: self-organization of stable category recognition codes for analog input patterns[J].Applied Optics, 1987, 26(23): 4919-4930.

[8]Dagher I, Georgiopoulos M, Heileman G L, et al. An ordering algorithm for pattern presentation in fuzzy ARTMAP that tends to improve generalization performance[J].IEEE Transactions on Neural Networks,1999,10(4): 768-778.

[9]Luukka P.Similarity classifier using similaritymea-sure derived from Yu’s norms in classification of medical data sets[J]. Computers in Biology and Medicine, 2007,37(8): 1133-1140.

[10]Liang J N, Yang S, Adam W. Invariant optimal feature selection: a distance discriminant and feature ranking based solution [J]. Pattern Recognition, 2008, 41(5): 1429-1439.

[11]Pierre Ripak. Vibroacoustic gear signatures with time-frequency spectrograms[EB/OL]. (2001-06-15)[2015-11-12].http://www.ulb.ac.be/polytech/laborulb/gearvi/gearjtfa.htm.

[12]Yang B S, Han T, An J L. ART-Kohonen neural network for fault diagnosis of rotating machinery[J].Mechanical Systems and Signal Processing, 2004, 18(3):645-657.

[责任编辑郑淑芳]

Application of clustering method based on ART and Yu norm to gears fault diagnosis

XuZengbing1,LiYourong1,WangZhigang1,XuanJianping2

(1.College of Machinery and Automation, Wuhan University of Science and Technology, Wuhan 430081, China;2. School of Mechanical Science and Engineering, Huazhong University of Science and Technology, Wuhan 430074, China)

Abstract:As the traditional clustering method needs to determine the number of classes in advance, a novel clustering method based on adaptive resonance theory (ART) and Yu norm that can self-adapt to determine the number of classes is proposed and validated by the diagnostic analysis of unlabeled faulty samples of gears. A feature parameter set that presents the fault-related information is extracted from different symptom domains, and some optimal features are selected by the distance discriminant technique. Having combined the merits of ART and Yu norm-based clustering method, the proposed clustering model is employed to diagnose the fault conditions of gears and found to be able to effectively classify the faulty samples of gears, having better diagnosis performance than the fuzzy ART.

Key words：gear; fault diagnosis;clustering method; ART; Yu norm; distance discriminant technique

收稿日期：2016-01-12

基金项目：国家自然科学基金资助项目(51405353).

作者简介：徐增丙(1981-)，男，武汉科技大学讲师，博士.E-mail:xuzengbing@163.com

中图分类号：TH165+.3

文献标志码：A

文章编号：1674-3644(2016)02-0116-05