2015高考福建理综17题解法探讨
邓思平
摘 要:力的空间积累效应和力的时间积累效应是问题的两个方面。此题中由合力的功较小得到终点速率大并不意味着合冲量一定较小,时间较短。本文采用类比法,通过分析简单的斜直轨道得到结论后合理外推到弧形轨道。
关键词:福建;理综;17题;类比法
中图分类号:G633.7 文献标识码:A 文章编号:1003-6148(2016)5-0045-3
原题 如图1,在竖直平面内,滑道ABC关于B点对称,且A、B、C三点在同一水平线上。若小滑块第一次由A滑到C,所用的时间为t1,第二次由C滑到A,所用时间为t2,小滑块两次的初速度大小相同且运动过程始终沿着滑道滑行,小滑块与滑道的动摩擦因数恒定,则( )
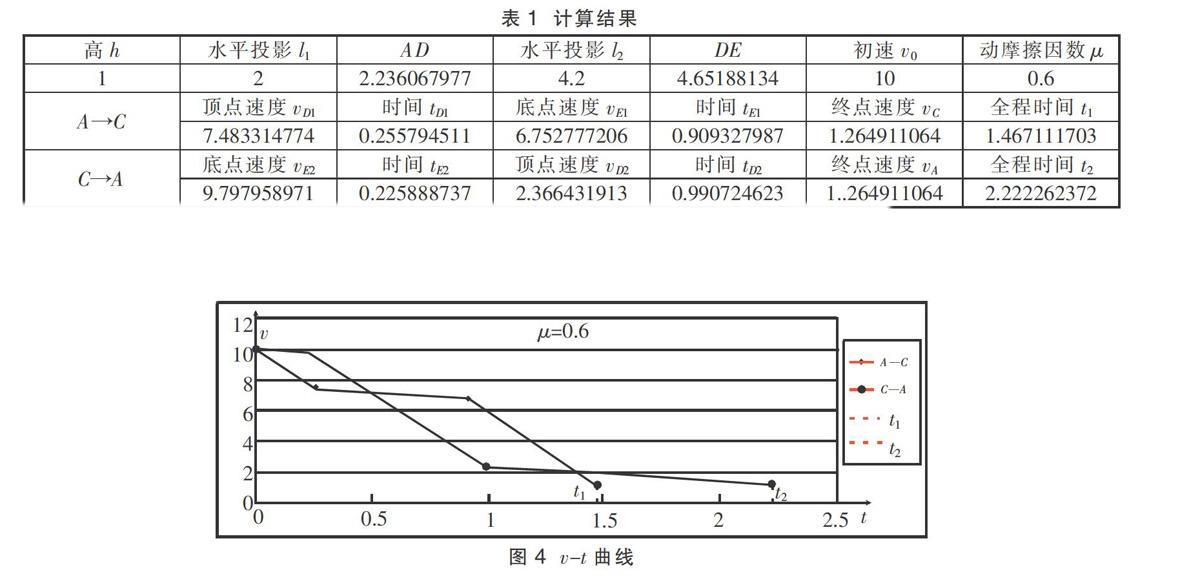
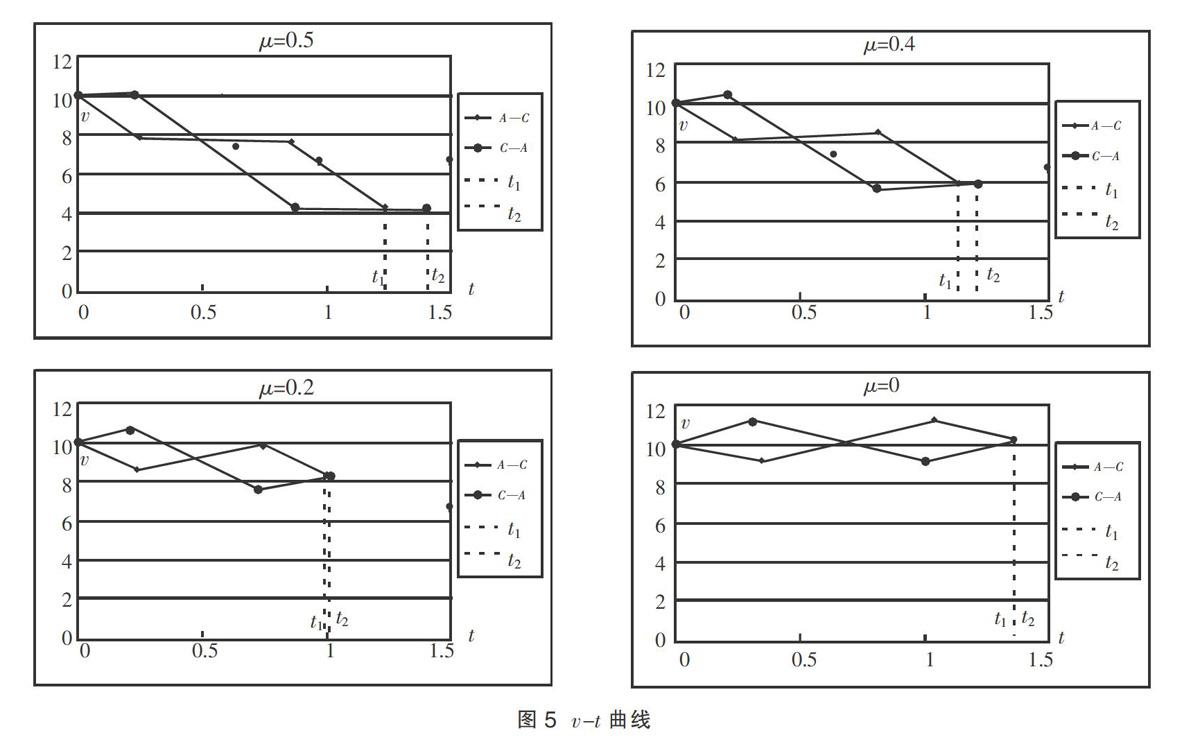
A.t1 C.t1>t2 D.无法比较t1、t2的大小 解析 在AB段,根据牛顿第二定律mg-FN=m,速度越大,滑块受支持力越小,摩擦力就越小。在BC段,根据牛顿第二定律FN-mg=m,速度越大,滑块受支持力越大,摩擦力就越大。由题意知从A运动到C相比从C运动到A,在AB段速度较大,在BC段速度较小。所以,从A到C运动过程受摩擦力较小,到达终点的速率较大,用时短。所以,A选项正确。 该解析应用牛顿第二定律分析比较摩擦力大小,应用动能定理比较终点速率。在路程和初速度大小相同的条件下,可推知终点速率较大的A到C运动过程用时较短。粗略看来,似乎没有什么问题。从网络回馈的信息来看,此解析也得到了普遍认同。果真如此吗?笔者细究之下,发现此解析存在一个问题。该解析错误地把力的空间积累效应和力的时间积累效应等同起来,力的空间积累效应(即做功)和力的时间积累效应(即冲量)是问题的两个方面,由合力的功较小得到终点速率大并不意味着合冲量一定较小,时间较短。而且,分析发现滑块的两个运动过程并不一定是单调的减速运动,在下坡段,可能加速也可能减速,中间过程相当复杂,不能简单地通过比较终点速率来比较运动时间。 正确方法应该是比较两个运动过程中滑块经过滑道上每一个相同位置的瞬时速率,即比较上行速率和下行速率的大小。比如,滑道光滑,动摩擦因数为零的理想情形,依据能量守恒可推知滑块经过每一个位置的上行速率总等于下行速率,那么A到C过程和C到A过程用时相同。 本题中,A到B过程相比B到A过程,摩擦力做负功较少。依据动能定理可确定,经过B点的下行速率大于上行速率。在拱形段的某个位置(如图2中的M点),A到M过程相比C到M过程,摩擦力做负功较少,经过M点的下行速率大于上行速率。还可推知 A到B过程和B到A过程的每一个相同位置,均是A到B过程经过的速率较大,则可得到A到B用时较短的结论。但是,在分析凹形段时却遇到困难,比如对于图2中的N点。A到N过程相比C到N过程,无法明确比较摩擦力做负功的多少,也就不知该位置的上行速率和下行速率的大小,因此不能比较B到C过程和C到B过程的用时。 为了解决这个问题,我们可以换用另一种思维方法:类比法。首先,把滑道简化成图3所示的斜直轨道ADBEC,B是轨道的对称点,D、E处处理成一段小圆弧,保证滑块始终在滑道上运动且不会发生撞击现象。应用动能定理和运动学知识求解出两个运动时间进行比较,然后将两种轨道进行类比推理,得到相关结论。 设轨道高为h,AD、CE段的水平投影为l1,DE段的水平投影为l2,动摩擦因数为μ,滑块的初速度大小为v0。为了方便作出v-t图像,除终点速率外,还需要求出D、E两个位置的速率以及滑块达到这些速率经过的时间。 同理可得,C到A过程的速率和到达时间分别是: 为了直观比较t1、t2的大小,笔者将轨道的参数h、l1、l2、μ、v0赋以合适的数值并导入到Excel表格中,然后运用Excel的公式和函数得到计算結果,再运用图表功能作出v-t图像得到最直观的结果。其中一次的计算结果如表1,表中数据全部采用国际单位。 由图4可见t1 由图5可见,随着μ的减小,t1 通过对滑块在斜直轨道ADBEC上运动情况的分析,可以得到如下结论:①滑块的运动比较复杂,下坡时可能加速也可能减速;② 两次过程中滑块在同一位置受到的摩擦力相同,终点速率也相同,但总用时并不同,总满足t1 对比两种轨道会发现,两种轨道的联系点有:① μ=0的理想情况,才有t1=t2;②弧形滑道相当于由在最高点和最低点附近改成弧形的斜直轨道;③滑块在弧形轨道最高点和最低点附近滑行时摩擦力的变化与μ增大引起摩擦力增大的斜直轨道相当;④斜直轨道上两次运动过程的终点速率相同,C到A过程用时较长。而弧形轨道C到A过程的终点速率较小,用时应该比斜直轨道还要长。据此,我们可以推测,滑块在斜直轨道上两次运动过程用时的大小关系也适用于弧形轨道,即原题答案为

