机电伺服系统齿隙补偿及终端滑模控制

李兵强　陈晓雷　林　辉　吕帅帅　马冬麒

(西北工业大学自动化学院　西安　710129)



机电伺服系统齿隙补偿及终端滑模控制

李兵强陈晓雷林辉吕帅帅马冬麒

(西北工业大学自动化学院西安710129)

摘要针对机电伺服系统存在的齿隙非线性及参数时变问题，提出无抖振全阶终端滑模控制补偿策略。设计连续可微函数逼近齿隙非线性环节的死区模型，将拟合误差、未建模动态及外部干扰叠加视为类似干扰项，建立拟合系统的状态空间模型，并划分为3个子系统，采用反演控制思想设计终端滑模控制器，使跟踪误差在有限时间内收敛到零点较小邻域，实现对齿隙的精确补偿。应用Lyapunov方法分析有限时间收敛条件及控制参数对系统的影响。通过实验验证了控制策略的有效性。

关键词：机电伺服系统永磁同步电机齿隙非线性滑模控制反演控制

0引言

齿隙非线性由机械传动机构中运动部件存在的间隙所引发，是动力传递过程不可避免的环节，也是影响机电伺服系统动态性能的主要因素。齿隙的存在会降低系统稳定性、引起振动与噪声，由于齿隙具有动态及不可微特性，且难于精确测量，控制补偿极为困难。从20世纪40年代至今，对齿隙非线性的研究伴随着控制理论的发展而不断深入[1，2]。近年来，随着高性能机电伺服系统的广泛应用及非线性控制理论的日趋成熟，含齿隙系统的控制设计成为控制领域历久弥新的研究课题，已取得了丰硕的研究成果[1-10]。

在控制输入端建立齿隙逆模型或近似可微逆模型，用以抵消齿隙非线性的影响，是应用最为广泛的补偿策略，与此相结合的控制算法包括自适应反演控制[3，4]、模糊控制[5]、神经网络控制[6]、鲁棒控制[7]、模型预测控制[8]、滑模控制[9]以及迭代学习控制[10]等。然而对于机电伺服系统而言，齿隙非线性环节难以简单折算到控制输入端，逆模型补偿策略无法适用。采用齿隙的死区模型描述力矩传递关系[2]更符合实际，由此含齿隙的非线性系统可视为非光滑三明治系统[11]。由于该系统结构复杂，对其控制难度较大，研究成果并不多见。文献[12]采用最优控制方法，针对系统接触阶段及齿隙阶段分别设计不同的控制策略，在补偿齿隙作用的同时可减小齿隙造成的机械冲击，但控制结构复杂，在齿隙较小时难以实现有限时间内的最优调节，工程实现难度较大。文献[13]采用可微函数拟合死区模型，并设计反演控制器，不足之处在于要求系统模型精确已知。文献[14]采用模糊函数逼近反推过程中产生的未知非线性函数以简化控制器设计，不足之处在于需采用拟合函数及其微分项作为状态变量，系统状态不具备清晰的物理涵义。

齿隙非线性是高性能机电伺服系统控制设计必须考虑的问题，要达到理想的齿隙补偿效果不仅依赖于算法本身，还依赖于对从动机构运动的精密测量以及对伺服电机的精确控制。现有文献均未考虑驱动机构自身的非线性特性以及负载变化对系统动态特性的影响。永磁同步电机(Permanent Magnet Synchronous Motor，PMSM)具有转矩脉动小、调速范围宽、功率密度高等优势，具有良好的发展前景[15]，适用于作为伺服系统的驱动机构，然而PMSM本身具有强耦合特点[16]，考虑其非线性特性的齿隙补偿控制设计更具有工程意义。

反推控制(Backstepping Control)的优势在于具有处理非匹配不确定的能力，保证系统的渐进稳定性，是处理高阶非线性系统强有力的工具。本文设计了连续可微函数逼近机电伺服系统中齿隙非线性的死区模型[17]，将拟合误差表达为类似干扰项[3]，建立了含齿隙环节的伺服系统状态空间模型。应用反推控制的分块设计方法，按物理结构将拟合模型划分为3个子系统进行控制设计，利用无抖振全阶滑模方法设计子系统控制器[18]，发挥滑模控制处理匹配不确定的优势，抑制未知扰动并得到平滑的虚拟控制量。利用反推方法完成交、直轴电流控制器设计。与常规逐层反推控制算法相比，设计步骤大为简化，同时控制设计具有终端滑模特性，可实现跟踪误差在有限时间内收敛，提升齿隙补偿效果。

1含齿隙的机电伺服系统数学模型

考虑齿隙作用，将PMSM驱动的机电伺服系统分解为驱动部分和从动部分，驱动部分包括伺服电机、驱动器、控制器和传感器。假设定子为三相对称绕组，转子为无阻尼绕组，气隙磁场呈正弦分布，磁路不饱和，不计磁滞和涡流损耗影响，表贴式PMSM的数学模型为[19]

(1)

式中，θ为转子机械角位移；ω为转子机械角速度；p为磁极对数；φf为耦合磁链；J为折算到电机轴上的等效转动惯量；id、iq分别为定子电流矢量的d、q轴分量；bm为粘性摩擦系数；Tl为折算到电机轴上的负载力矩；R为绕组电阻；L为绕组电感；ud、uq分别为定子电压矢量的d、q轴分量。

从动部分的动力学方程为

(2)

式中，Jl为负载转动惯量；θl为负载输出转角；bl为粘性阻尼系数；η为减速比；Tf为负载力矩。

齿隙作用于连接驱动部分和从动部分的传动机构中，Tl与传动机构相对位移的关系可由死区模型表示为[13]

(3)

式中，Δθ=θ-ηθl； α为1/2齿隙宽度；k为主从动齿轮啮合处的刚度系数。采用如下连续可微函数拟合死区模型[17]

(4)

式中，τ为拟合常数。定义拟合误差为

TΔ=Tl-Ts=Tl-kΔθ-4kαε(Δθ)

(5)

Tl=k(θ-ηθl)+4kαε(θ-ηθl)+TΔ

(6)

(7)

将式(6)代入式(1)，机械方程可写为

(8)

电流环动态特性与电磁转矩相关，是衡量伺服性能的关键指标。随着电机运行中绕组温度的变化，电机的电磁特性将发生改变(如电阻、电感等参数会有较大变动)，因此将模型误差及未建模动态视为未知干扰。定义状态变量x=[θl, ωl, θ, ω, iq, id]，联立式(1)、式(2)、式(7)和式(8)可得整体系统状态方程为

(9)

式中，y为系统输出；uq、ud为控制量；di为未知扰动，i=1,…,4。

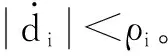
2控制器设计

2.1从动子系统控制设计

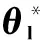
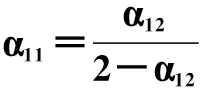
(11)

(12)

(13)

(14)

(15)

可知从动子系统为渐近稳定且滑模面可在有限时间内到达[18]，随后系统可在有限时间内，任意初始条件z1(0)≠0下沿滑模面运动到z1=0。

2.2PMSM机械子系统控制设计

(16)

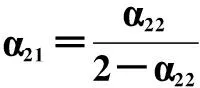
(17)

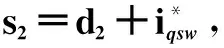
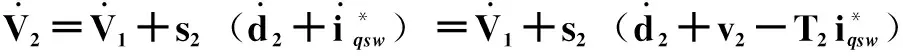
(18)

(19)

同理可知系统渐近稳定。

2.3PMSM电气子系统设计

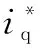
(20)

(21)

式中，c3、 c4为正实数；0<α3,α4<1。

设计交轴电压uq为

(22)

设计直轴电压ud为

(23)

2.4稳定性分析

引理1：若a1,a2,…,an皆为正实数，δ∈(0,2)，则下列不等式成立[21]

(24)

引理2：若连续可微Lyapunov函数V(t)满足如下不等式[22]

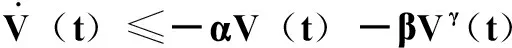
(25)

式中，α, β>0，0<γ<1，则V(t)可在有限时间内收敛到零点，收敛时间为

(26)

定理1：对式(9)所示含齿隙的机电伺服系统，虚拟控制量设计如式(11)和式(17)所示，采用式(22)和式(23)所示反馈控制律，若满足假设1和假设2，取适当的滑模面参数及控制器参数ηi、 κi，则滑模面有限时间内可达，跟踪误差随后在有限时间内收敛为零。

证明：选取整体系统的Lyapunov函数为

(27)

对式(27)求微分得

(28)

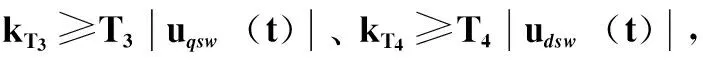
(29)

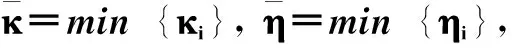
(30)

由引理2可知，系统可在有限时间内到达滑模面

(31)

结合终端滑模面性质，可知跟踪误差随后在有限时间收敛为零。终端滑模控制具有较强的鲁棒性，但齿隙补偿效果及误差收敛速度仍依赖模型先验知识，通过对参数τ的合理设置提高齿隙拟合准确度可缩小TΔ，从而减小V(t0)，缩短滑模面到达时间。

3实验验证

3.1实验平台

为验证控制算法的有效性，在自行研制的机电伺服系统实验台上进行实验，平台结构如图1所示。实验平台主要由驱动电机、控制器、传感器、传动机构、减速齿轮及电源等构成。为检测系统在时变载荷下的控制性能，设计负载模拟器作为加载装置，实现对负载力矩的闭环控制。控制器采用TMS320F2812，逆变单元采用IGBT组成全桥结构，通过光电编码器进行位置测量。驱动电机采用表贴式PMSM，参数为：p=5，φf=0.143 Wb，J=2.84×10-4kg·m2，bm=1.0×10-4N·m/rad/s，R=1.73 Ω，L=7 mH，额定转矩Te=4.7 N·m，直流母线电压Vdc=270 V。从动机构参数为：Jl=0.4 kg·m2，bl=0.12 N·m/(rad/s)，η=30。齿隙参数为：k=200 N·m/rad，τ=22，α=0.023 rad。

图1　实验平台Fig.1　Experimental platform

3.2与线性控制对比结果

与不考虑齿隙作用的线性控制进行对比，PMSM速度环及电流环采用PI控制器，位置环采用PID控制，反馈信号为θl。 实验结果如图2所示。

由图2a、图2b可知，当指令信号运动方向发生改变时，齿隙导致从动机构实际运动出现滞后效应，跟踪误差逐渐增大，在渡过齿隙阶段后由于冲击作用导致跟踪误差呈现明显的振荡，随后在控制作用下误差逐渐变小。由图2c、图2d可看出，齿隙非线性对电机转速和电流产生持续的干扰作用。

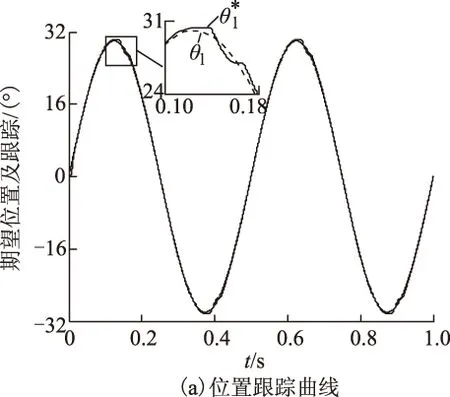
图2　线性控制实验结果Fig.2　Results of classical linear control method

验证本文方法的齿隙补偿效果，滑模面参数设置为：c12=c22=7，c11=c21=10，c3=c4=5，α12=α22=α3=α4=9/16，α11=α21=9/23； 控制器参数设置为：Ti=0.1，kdi=4，kT1+η1=kT2+η2=6，kT3+η3=kT4+η4=3。 κ1=κ2=200，κ3=κ4=100。 实验结果如图3所示。

图3　本文方法实验结果Fig.3　Results of the proposed method

由图3a可知，考虑齿隙非线性因素进行控制律设计，有效抑制了齿隙影响，使跟踪误差显著减小，控制质量得到显著提升。由图3b、图3c可知，主动对齿隙进行补偿时，在齿隙作用阶段存在控制量激增的过程，使系统快速渡过齿隙阶段，消除齿隙影响。

3.3齿隙拟合参数τ对系统影响

由式(3)和式(4)可知，当齿隙特性完全确定时，τ是惟一决定拟合准确度的参数，文献[14]得到特定条件下的最佳τ取值方法。文献[17]采用滑模观测器辨识齿隙参数，从实验结果来看，与理想齿隙模型相比，真实传动机构的齿隙特征更为复杂。考虑齿隙模型参数时变将导致问题复杂性，τ取不同值时的跟踪误差如图4所示。

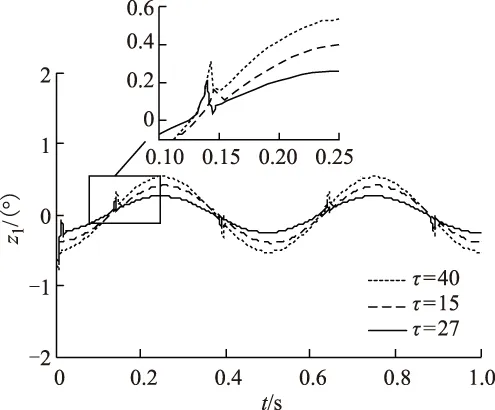
图4　不同τ值控制结果Fig.4　Results with different τ

对比图3a可看出跟踪误差有一定程度的增加，这是由于可微函数拟合准确度有所降低，导致非匹配不确定项的增大，但滑模控制具有很强的干扰抑制能力，合理调节τ仍可实现较好的控制效果，这也体现出本文算法与常规反演算法相比具有抗扰动能力及鲁棒性的优势。

4结论

针对PMSM驱动的机电伺服系统中存在的齿隙非线性，基于反演控制思想，设计全阶无抖振终端滑模控制器，得到以下结论：

1)本文算法可有效实现齿隙补偿，在负载和齿隙特征发生变化时具有强鲁棒性。

2)利用分块设计思想虚拟控制量，可降低常规反演或动态面控制需逐层递推的复杂程度，适用于高阶非线性系统，与高阶滑模控制器设计相比，避免了精确线性化过程依赖模型准确度的困难。

3)考虑伺服电机本身的非线性因素，设计无抖振滑模控制得到连续的电流控制律，并分析了影响齿隙补偿控制效果的若干因素，研究方法亦可推广到其他驱动机构的伺服系统及多关节伺服系统齿隙补偿设计。

参考文献

[1]Gang T，Kokotovic P V.Adaptive control of systems with backlash[J].Automatica，1993，29(2)：323-335.

[2]Mattias N，Per G.Controlling mechanical systems with backlash：a survey[J].Automatica，2002，38(10)：1633-1649.

[3]Zhou J，Wen C Y，Zhang Y.Adaptive backstepping control of a class of uncertain nonlinear systems with unknown backlash-like hysteresis[J].IEEE Transactions on Automatic Control，2004，49(10)：1751-1759.

[4]Zhou J，Zhang C J，Wen C Y.Robust adaptive output control of uncertain nonlinear plants with unknown backlash nonlinearity[J].IEEE Transactions on Automatic Control，2007，52(3)：503-509.

[5]Liu Y J，Tong S C.Adaptive fuzzy control for a class of nonlinear discrete-time systems with backlash[J].IEEE Transactions on Fuzzy Systems，2014，22(5)：1359-1365.

[6]Wang H Q，Chen B，Liu K F，et al.Adaptive neural tracking control for a class of nonstrict-feedback stochastic nonlinear systems with unknown backlash-like hysteresis[J].IEEE Transactions on Neural Networks and Learning Systems，2014，25(5)：947-958.

[7]Tarbouriech S，Queinnec I，Prieur C.Stability analysis and stabilization of systems with input backlash[J].IEEE Transactions on Automatic Control，2014，59(2)：488-494.

[8]Philipp R，Thomas B，Miroslav B，et al.Hybrid approach to modeling，control and state estimation of mechanical systems with backlash[J].International Journal of Control，2007，80(11)：1729-1740.

[9]Corradini M L，Orlando G.Robust stabilization of nonlinear uncertain plants with backlash or dead zone in the actuator[J].IEEE Transactions on Control Systems Technology，2002，10(1)：158-166.

[10]朱胜，孙明轩，何熊熊.齿隙非线性输入系统的迭代学习控制[J].自动化学报，2011，37(8)：1014-1017.

Zhu Sheng，Sun Mingxuan，He Xiongxiong.Iterative learning control of a class of nonlinear systems with input backlash[J].Acta Automatica Sinica，2011，37(8)：1014-1017.

[11]Taware A，Tao G，Teolis C.Design and analysis of a hybrid control scheme for sandwich nonsmooth nonlinear systems[J].IEEE Transactions on Automatic Control，2002，47(1)：145-150.

[12]Tao G，Ma X L，Ling Y.Optimal and nonlinear decoupling control of systems with sandwiched backlash[J].Automatica，2001，37(2)：165-176.

[13]Shi Z G，Zuo Z Y.Backstepping control for gear transmission servo systems with backlash nonlinearity[J].IEEE Transactions on Automation Science and Engineering，2015，12(2)：752-757.

[14]杜仁慧，吴益飞，陈威，等.考虑齿隙伺服系统的反步自适应模糊控制[J].控制理论与应用，2013，30(2)：254-260.

Du Renhui，Wu Yifei，Chen Wei，et al.Adaptive backstepping fuzzy control for servo systems with backlash[J].Control Theory & Applications，2013，30(2)：254-260.

[15]付培华，陈振，丛炳龙，等.基于反步自适应滑模控制的永磁同步电机位置伺服系统[J].电工技术学报，2013，28(9)：288-293.

Fu Peihua，Chen Zhen，Cong Binglong，et al.A position servo system of permanent magnet synchronous motor based on back-stepping adaptive sliding mode control[J].Transactions of China Electrotechnical Sosiety，2013，28(9)：288-293.

[16]黄庆，黄守道，伍倩倩，等.基于模糊自抗扰控制器的永磁同步电动机伺服系统[J].电工技术学报，2013，28(9)：294-301.

Huang Qing，Huang Shoudao，Wu Qianqian，et al.PMSM servo system based on fuzzy active-disturbance rejection controller[J].Transactions of China Electrotechnical Sosiety，2013，28(9)：294-301.

[17]Merzouki R，Davila J A，Fridman L，et al.Backlash phenomenon observation and identification in electromechanical system[J].Control Engineering Practice，2007，15(4)：447-457.

[18]Feng Y，Han F L，Yu X H.Chattering free full-order sliding-mode control[J].Automatica，2014，50(4)：1310-1314.

[19]许叙遥，林辉.基于动态滑模控制的永磁同步电机位置速度一体化设计[J].电工技术学报，2014，29(5)：77-83.

Xu Xuyao，Lin Hui.Integrated design for permanent magnet synchronous motor servo systems based on dynamic sliding mode control[J].Transactions of China Electrotechnical Sosiety，2014，29(5)：77-83.

[20]Levant A.Chattering analysis[J].IEEE Transactions on Automatic Control，2010，55(6)：1380-1389.

[21]Yu S H，Yu X H，Bijan S，et al.Continuous finite-time control for robotic manipulators with terminal sliding mode[J].Automatica，2005，41(11)：1957-1964.

[22]Nekoukar V，Erfanian A.Adaptive fuzzy terminal sliding mode control for a class of MIMO uncertain nonlinear systems[J].Fuzzy Sets and Systems，2011，179(1)：34-49.

作者简介

李兵强男，1982年生，副教授，博士，研究方向为电机伺服控制理论、迭代学习控制。

E-mail：libingqiang@nwpu.edu.cn

陈晓雷男，1980年生，博士研究生，研究方向为伺服系统及非线性控制。

E-mail：chenilc@126.com(通信作者)

Terminal Sliding Mode Control for Mechatronic Servo Systems with Backlash Nonlinearity Compensation

Li BingqiangChen XiaoleiLin HuiLü ShuaishuaiMa Dongqi

(School of AutomationNorthwestern Polytechnical UniversityXi’an710129China)

AbstractIn order to overcome the problem of backlash nonlinearity and parameter time-varying in mechatronic servo systems，a chattering free full order sliding mode control strategy is proposed.The dead zone model of the backlash nonlinearity can be approximated by the proposed differentiable function.The superposition of the approximation error，the unmodeled dynamics，and the external disturbance can be regarded as the disturbance-like term.The continuous state-space model of the servo systems with the backlash nonlinearity is established and divided into three subsystems.The terminal sliding mode control law is constructed based on the backstepping design principle，which can make the tracking error converge to an arbitrarily small residual within finite time and achieve the precise compensation of the backlash.The finite-time convergence condition of the closed-loop system is analyzed using the Lyapunov theory.The experimental test verifies the effectiveness of the proposed control approach.

Keywords：Mechatronic servo systems，permanent magnet synchronous motor，backlash nonlinearity，sliding mode control，backstepping control

中图分类号：TP273

国家自然科学基金(51407143)、高等学校博士学科点专项科研基金(20136102120049)、陕西省自然科学基础研究计划(2014JQ7264，2015JM5227)、中央高校基本科研业务费(3102014JCQ01066)和陕西省微特电机及驱动技术重点实验室开放基金(2013SSJ1002)资助项目。

收稿日期2015-08-11改稿日期2016-01-12